Решение задач с помощью кругов Эйлера

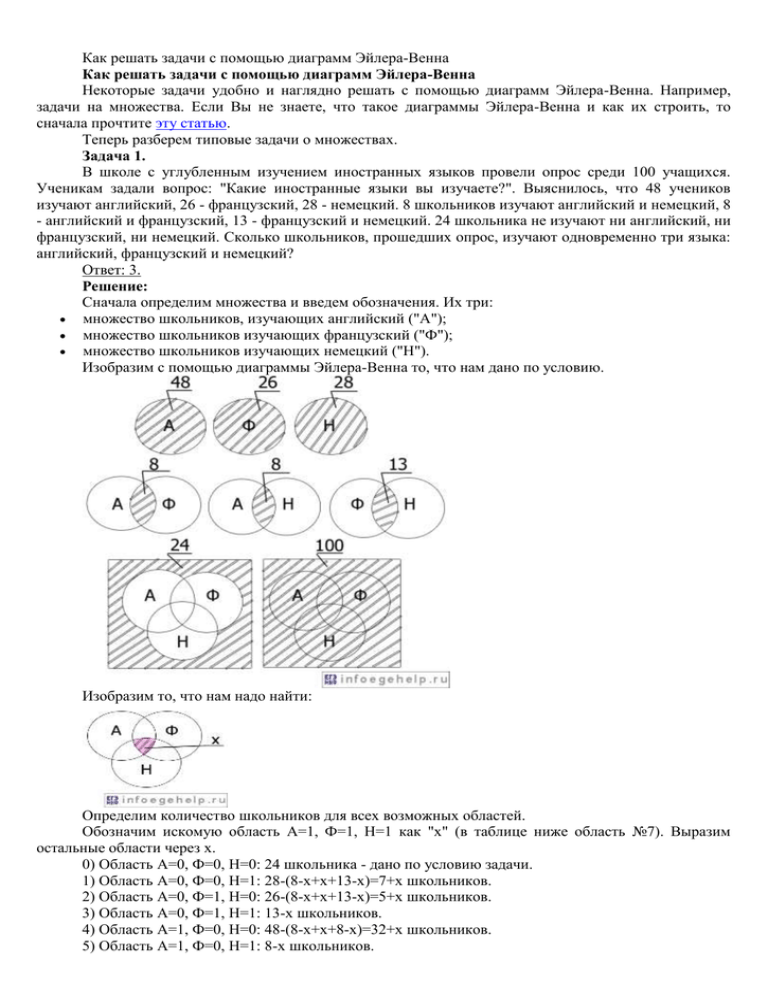
Как решать задачи с помощью диаграмм Эйлера-Венна
Как решать задачи с помощью диаграмм Эйлера-Венна
Некоторые задачи удобно и наглядно решать с помощью диаграмм Эйлера-Венна. Например,
задачи на множества. Если Вы не знаете, что такое диаграммы Эйлера-Венна и как их строить, то
сначала прочтите эту статью.
Теперь разберем типовые задачи о множествах.
Задача 1.
В школе с углубленным изучением иностранных языков провели опрос среди 100 учащихся.
Ученикам задали вопрос: "Какие иностранные языки вы изучаете?". Выяснилось, что 48 учеников
изучают английский, 26 - французский, 28 - немецкий. 8 школьников изучают английский и немецкий, 8
- английский и французский, 13 - французский и немецкий. 24 школьника не изучают ни английский, ни
французский, ни немецкий. Сколько школьников, прошедших опрос, изучают одновременно три языка:
английский, французский и немецкий?
Ответ: 3.
Решение:
Сначала определим множества и введем обозначения. Их три:
 множество школьников, изучающих английский ("А");
 множество школьников изучающих французский ("Ф");
 множество школьников изучающих немецкий ("Н").
Изобразим с помощью диаграммы Эйлера-Венна то, что нам дано по условию.
Изобразим то, что нам надо найти:
Определим количество школьников для всех возможных областей.
Обозначим искомую область А=1, Ф=1, Н=1 как "х" (в таблице ниже область №7). Выразим
остальные области через х.
0) Область А=0, Ф=0, Н=0: 24 школьника - дано по условию задачи.
1) Область А=0, Ф=0, Н=1: 28-(8-х+х+13-х)=7+х школьников.
2) Область А=0, Ф=1, Н=0: 26-(8-х+х+13-х)=5+х школьников.
3) Область А=0, Ф=1, Н=1: 13-х школьников.
4) Область А=1, Ф=0, Н=0: 48-(8-х+х+8-х)=32+х школьников.
5) Область А=1, Ф=0, Н=1: 8-х школьников.
6) Область А=1, Ф=1, Н=0: 8-х школьников.
Запишем значения областей в таблицу:
№
области
Коли
А Фчество
Н
школьников
0
0
0
0
24
1
0
0
1
7+х
2
0
1
0
5+х
3
0
1
1
13-х
4
1
0
0
32+х
5
1
0
1
8-х
6
1
1
0
8-х
7
1
1
1
х
Изобразим значения для всех областей с помощью диаграммы:
Определим х:
24+7+(х+5)+х+(13-х)+(32+х)+(8-х)+(8-х)+х=100.
х=100-(24+7+5+13+32+8+8)=100-97=3.
Получили, что 3 школьника изучают одновременно три языка: английский, французский и
немецкий.
Так будет выглядеть диаграмма Эйлера-Венна при известном х:
Задача 2.
На олимпиаде по математике школьникам предложили решить три задачи: одну по алгебре, одну
по геометрии, одну по тригонометрии. В олимпиаде участвовало 1000 школьников. Результаты
олимпиады были следующие: задачу по алгебре решили 800 участников, по геометрии - 700, по
тригонометрии - 600. 600 школьников решили задачи по алгебре и геометрии, 500 - по алгебре и
тригонометрии, 400 - по геометрии и тригонометрии. 300 человек решили задачи по алгебре, геометрии
и тригонометрии. Сколько школьников не решило ни одной задачи?
Ответ: 100.
Решение:
Сначала определим множества и введем обозначения. Их три:
 множество задач по алгебре ("А");
 множество задач по геометрии ("Г");

множество задач по тригонометрии ("Т").
Изобразим с помощью диаграммы Эйлера-Венна то, что нам дано по условию:
Изобразим то, что нам надо найти:
Определим количество школьников для всех возможных областей.
Обозначим искомую область А=0, Г=0, Т=0 как "х" (в таблице ниже область №0).
Найдем остальные области:
1) Область А=0, Г=0, Т=1: школьников нет.
2) Область А=0, Г=1, Т=0: школьников нет.
3) Область А=0, Г=1, Т=1: 100 школьников.
4) Область А=1, Г=0, Т=0: школьников нет.
5) Область А=1, Г=0, Т=1: 200 школьников.
6) Область А=1, Г=1, Т=0: 300 школьников.
7) Область А=1, Г=1, Т=1: 300 школьников.
Запишем значения областей в таблицу:
№
области
Коли
А Г
чество
Т
школьников
0
0
0
0
х
1
0
0
1
0
2
0
1
0
0
3
0
1
1
100
4
1
0
0
0
5
1
0
1
200
6
1
1
0
300
7
1
1
1
300
Изобразим значения для всех областей с помощью диаграммы:
Определим х:
х=U-(A V Г V Т), где U-универсум.
U=1000.
A V Г V Т=0+0+0+300+300+200+100=900.
x=1000-900=100.
Получили, что 100 школьников не решило ни одной задачи.
Задача 3.
На олимпиаде по физике школьникам предложили решить три задачи: одну по кинематике, одну
по термодинамике, одну по оптике. Результаты олимпиады были следующие: задачу по кинематике
решили 400 участников, по термодинамике - 350, по оптике - 300. 300 школьников решили задачи по
кинематике и термодинамике, 200 - по кинематике и оптике, 150 - по термодинамике и оптике. 100
человек решили задачи по кинематике, термодинамике и оптике. Сколько школьников решило две
задачи?
Ответ: 350.
Решение:
Сначала определим множества и введем обозначения. Их три:
 множество задач по кинематике ("К");
 множество задач по термодинамике ("Т");
 множество задач по оптике ("О").
Изобразим с помощью диаграммы Эйлера-Венна то, что нам дано по условию:
Изобразим то, что нам надо найти:
Определим количество школьников для всех возможных областей:
0) Область К=0, Т=0, О=0: не определено.
1) Область К=0,Т=0, О=1: 50 школьников.
2) Область К=0, Т=1, О=0: школьников нет.
3) Область К=0, Т=1, О=1: 50 школьников.
4) Область К=1, Т=0, О=0: школьников нет.
5) Область К=1, Т=0, О=1: 100 школьников.
6) Область К=1, Т=1, О=0: 200 школьников.
7) Область К=1, Т=1, О=1: 100 школьников.
Запишем значения областей в таблицу:
№
области
Коли
К Тчество
О
школьников
0
0
0
0
-
1
0
0
1
50
2
0
1
0
0
3
0
1
1
50
4
1
0
0
0
5
1
0
1
100
6
1
1
0
200
7
1
1
1
100
Изобразим значения для всех областей с помощью диаграммы:
Определим х.
х=200+100+50=350.
Получили, 350 школьников решило две задачи.
Задача 4.
Среди прохожих провели опрос. Был задан вопрос: "Какое домашнее животное у Вас есть?". По
результатам опроса выяснилось, что у 150 человек есть кошка, у 130 - собака, у 50 - птичка. У 60
человек есть кошка и собака, у 20 - кошка и птичка, у 30 - собака и птичка. У 70 человек вообще нет
домашнего животного. У 10 человек есть и кошка, и собака, и птичка. Сколько прохожих приняли
участие в опросе?
Ответ: 300.
Решение:
Сначала определим множества и введем обозначения. Их три:
 множество людей, у которых есть кошка ("К");
 множество людей, у которых есть собака ("С");
 множество людей, у которых есть птичка ("П").
Изобразим с помощью диаграммы Эйлера-Венна то, что нам дано по условию:
Изобразим то, что нам надо найти:
Определим количество человек для всех возможных областей:
0) Область К=0, С=0, П=0: 70 человек.
1) Область К=0, С=0, П=1: 10 человек.
2) Область К=0, С=1, П=0: 50 человек.
3) Область К=0, С=1, П=1: 20 человек.
4) Область К=1, С=0, П=0: 80 человек.
5) Область К=1, Т=0, О=1: 10 человек.
6) Область К=1, Т=1, О=0: 50 человек.
7) Область К=1, Т=1, О=1: 10 человек.
Запишем значения областей в таблицу:
№
области
Коли
К Cчество
П
человек
0
0
0
0
70
1
0
0
1
10
2
0
1
0
50
3
0
1
1
20
4
1
0
0
80
5
1
0
1
10
6
1
1
0
50
7
1
1
1
10
Изобразим значения для всех областей с помощью диаграммы:
Определим х:
х=U (универсум)
U=70+10+50+20+80+10+50+10=300.
Получили, что 300 человек приняли участие в опросе.
Задача 5.
На одну специальность в одном из ВУЗов поступало 120 человек. Абитуриенты сдавали три
экзамена: по математике, по информатике и русскому языку. Математику сдали 60 человек,
информатику - 40. 30 абитуриентов сдали математику и информатику, 30 - математику и русский язык,
25 - информатику и русский язык. 20 человек сдали все три экзамена, а 50 человек - провалили. Сколько
абитуриентов сдали русский язык?
Ответ: 35.
Решение:
Сначала определим множества и введем обозначения. Их три:
 множество абитуриентов, сдавших математику ("М");
 множество абитуриентов, сдавших информатику ("И");
 множество абитуриентов, сдавших русский язык ("Р");
Изобразим с помощью диаграммы Эйлера-Венна то, что нам дано по условию:
Изобразим то, что нам надо найти:
Определим количество абитуриентов для всех возможных областей.
Обозначим искомую область как "х".
0) Область М=0, И=0, Р=0: 50 абитуриентов.
1) Область М=0, И=0, Р=1: х-35 абитуриентов.
2) Область М=0, И=1, Р=0: 5 абитуриентов.
3) Область М=0, И=1, Р=1: 20 абитуриентов.
4) Область М=1, И=0, Р=0: 80 абитуриентов.
5) Область М=1, И=0, Р=1: 10 абитуриентов.
6) Область М=1, И=1, Р=0: 50 абитуриентов.
7) Область М=1, И=1, Р=1: 10 абитуриентов.
Запишем значения областей в таблицу:
№
области
Колич
М И
ество
Р
абитуриентов
0
0
0
0 50
1
0
0
1 х-35
2
0
1
0 5
3
0
1
1 5
4
1
0
0 20
5
1
0
1 10
6
1
1
0 10
7
1
1
1 20
Изобразим значения для всех областей с помощью диаграммы:
Определим х:
х=120-50-(20+10+5)=35.
Получили, что 35 абитуриентов сдали русский язык.
Так будет выглядеть диаграмма Эйлера-Венна при известном х:
Перейти к разбору задач на множества из демо ЕГЭ (определение количества страниц по
запросу поискового сервера):
 В12-2012
 В9-2011
 В10-2010
 В10-2009
Перейти к другим задачам демо ЕГЭ.
http://infoegehelp.ru/index.php?option=com_content&view=article&id=241:2012-02-18-15-0407&catid=40:2011-12-18-14-30-56&Itemid=65








Важно
Демо варианты ЕГЭ
Учим числа: 2 в степени
Биты, байты, килобайты
Решение задач
Быстрый поиск задачи
Задачи вне основных разделов информатики
Разделы информатики
 Системы счисления
Алгебра логики
 Программирование
Кодирование
информации
 Компьютерные сети и Интернет
Электронные таблицы
(Excel)

Базы данных

Графы


Файловая система
Устройство компьютера
ПО компьютера
Алгебра логики
