А.П.Ерохина. Методические указания по лаб.работам. (2 Мб, doc)
реклама
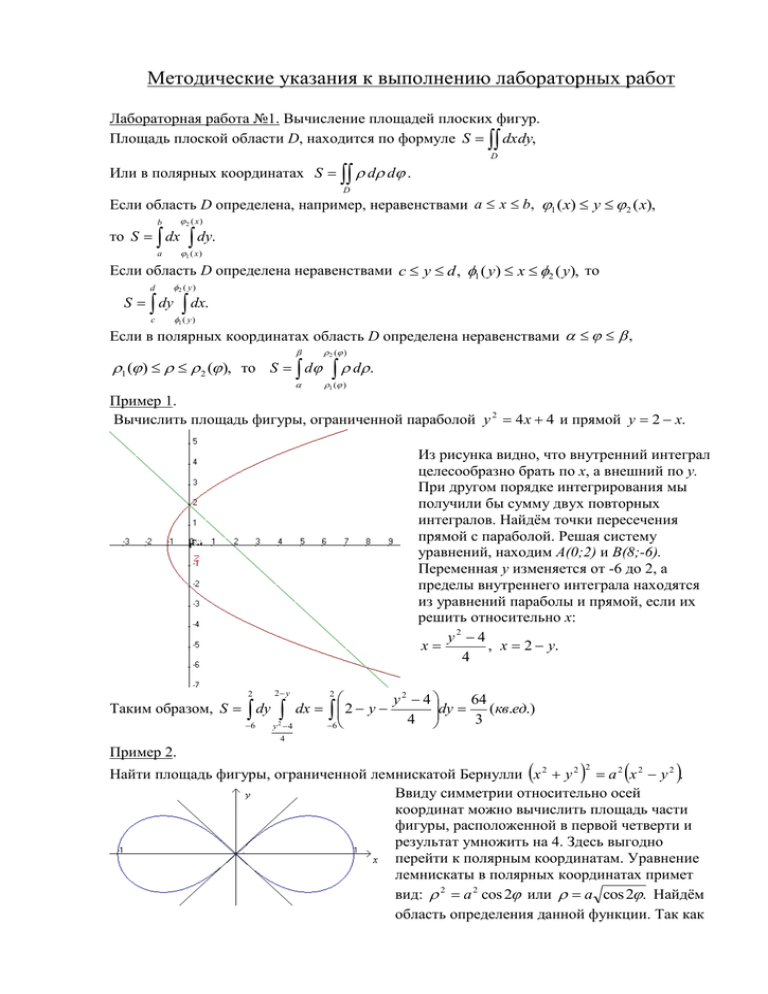
Методические указания к выполнению лабораторных работ Лабораторная работа №1. Вычисление площадей плоских фигур. Площадь плоской области D, находится по формуле S dxdy, D Или в полярных координатах S d d . D Если область D определена, например, неравенствами a x b, 1 ( x) y 2 ( x), b 2 ( x ) a 1 ( x ) то S dx dy. Если область D определена неравенствами c y d , 1 ( y) x 2 ( y), то d 2 ( y ) c 1 ( y ) S dy dx. Если в полярных координатах область D определена неравенствами , 1 ( ) 2 ( ), то S d 2 ( ) d . 1( ) Пример 1. Вычислить площадь фигуры, ограниченной параболой y 2 4 x 4 и прямой y 2 x. Из рисунка видно, что внутренний интеграл целесообразно брать по x, а внешний по y. При другом порядке интегрирования мы получили бы сумму двух повторных интегралов. Найдём точки пересечения прямой с параболой. Решая систему уравнений, находим A(0;2) и B(8;-6). Переменная y изменяется от -6 до 2, а пределы внутреннего интеграла находятся из уравнений параболы и прямой, если их решить относительно x: y2 4 x , x 2 y. 4 2 y y2 4 64 dy Таким образом, S dy dx 2 y (кв.ед.) 4 3 6 6 y 2 4 2 2 4 Пример 2. 2 Найти площадь фигуры, ограниченной лемнискатой Бернулли x 2 y 2 a 2 x 2 y 2 . Ввиду симметрии относительно осей координат можно вычислить площадь части фигуры, расположенной в первой четверти и результат умножить на 4. Здесь выгодно перейти к полярным координатам. Уравнение лемнискаты в полярных координатах примет вид: 2 a 2 cos 2 или a cos 2. Найдём область определения данной функции. Так как cos 2 0, то 2 2n 2 При n 0 получим при n 1 получим 4 Получаем S 4 d 0 4 4 2 2n и 4 n 4 n . , т.е. правая петля лемнискаты, 3 5 , (левая петля). 4 4 d 2 a cos 2 0 4 2 a cos 2 0 0 d 2a cos 2 d 2a sin2 2 4 2 4 a2. 2 0 0 Лабораторная работа №2. Вычисление объёмов тел. Объём цилиндрического тела, ограниченного сверху поверхностью z f ( x, y ) , снизу плоскостью z 0 и сбоку цилиндрической поверхностью вырезающей на плоскости xOy область D, вычисляется по формуле V f ( x, y)dxdy. D Объём области V можно находить и с помощью тройного интеграла V dv или V dxdydz в декартовых координатах, V V V d d dz в цилиндрических координатах, V V r 2 sin d d dr в сферических координатах. V Во избежание возможных ошибок при вычислении объёма тела полезно сделать пространственный рисунок, который давал бы представление о форме данного тела. Если же тело построить не удаётся, то можно ограничиться хотя бы рисунком, изображающим проекцию данного тела на одну из координатных плоскостей (область интегрирования двойного интеграла). Однако и в этом случае необходимо представить себе, какая поверхность ограничивает тело сверху. Пример 3. Вычислить объём тела, ограниченного поверхностями z 2 x y, y x 2 , y x и z 0. Сверху тело ограничено плоскостью z 2 x y, снизу плоскостью xOy, с боков – цилиндрической поверхностью y x 2 и плоскостью y x . Основанием тела, т. Е. областью интегрирования является плоская область D, ограниченная параболой y x 2 и прямой y x . y 2 x V dx (2 x y )dy 2 y xy dx x2 2 2 0 x 0 1 x 1 1 x 2 2 x 4 2 3 2x x 2x x dx 2 2 0 1 x4 7x2 7 x3 2 x dx . 2 2 20 0 Пример 4. Вычислить объём тела, вырезанного цилиндром x 2 y 2 4 x из шара x 2 y 2 z 2 16 . Заметим, так как оба уравнения поверхностей содержат сумму квадратов x 2 y 2 , то удобнее перейти к цилиндрическим координатам x 2 y 2 4 x 4 cos и Уравнение сферы x 2 y 2 z 2 16 2 z 2 16 или z 16 z 2 . В силу симметрии тела можно ограничиться вычислением четвёртой части тела, расположенной в первом октанте. Область интегрирования – полукруг в первой 2 4 cos 0 0 четверти. V 4 d 3 42 (16 2 ) 2 30 16 2 d 4 cos d 0 128 2 ( ) 3 3 Пример 5. Вычислить объём тела, ограниченного поверхностями hz x 2 y 2 и z h . Решение. Снизу тело ограничено x2 y2 параболоидом z , сверху h плоскостью z h и проектируется в круг x 2 y 2 h 2 плоскости xOy . Используем цилиндрические координаты, в которых 2 уравнение параболоида примет вид z . h Объём тела равен V d d dz V 2 h h 2 0 0 2 0 d d dz h 2 2 3 2 3 h 2 4 3 d d h h d h . d h 2 4h 2 h 4 0 2 0 0 0 h h Лабораторная работа №3. Вычисление площади поверхности. Если поверхность задана уравнением z z ( x, y ) и её проекция на плоскость xOy есть область D, то площадь поверхности вычисляется по формуле S ds или . S DxOy 2 2 z z 1 dxdy . x y Аналогично, если поверхность задана уравнением x x( y, z ) , то 2 S D yOz 2 x x 1 dydz , где D yOz проекция поверхности на плоскость yOz . z y Если уравнение поверхности имеет вид y y ( x, z ), то S 2 DxOz 2 y y 1 dxdz , x z где DxOz проекция поверхности на плоскость xOz . Пример 6. Найти площадь части конуса z x 2 y 2 , заключённой внутри цилиндра z x ; x 2 y 2 2 x. Находим частные производные из уравнения конуса: 2 2 x x y z y y x2 y2 . Областью интегрирования D является круг, ограниченный окружностью x 2 y 2 2 x или ( x 1) 2 y 2 1 , то есть центр окружности в точке (1;0) и радиус равен 1. Двойной интеграл удобнее считать в полярных координатах. Окружность x 2 y 2 2 x в полярных координатах имеет вид 2 cos . Тогда S 1 x2 y2 dxdy = 2 dxdy S ( D) 2 (Площадь круга равна R 2 . x y x y D У нас R 1 ). Лабораторная работа № 4. Вычисление длины кривой 2 2 2 2 D x x(t ) Если плоская кривая AB задана параметрическими уравнениями . t [ ; ] , где y y (t ) x(t ) и y (t ) дифференцируемые функции, причём точке A соответствует t , точке B значение t , то длина кривой находится по формуле l ( x ) 2 ( y ) 2 dt. x x(t ) Для пространственной кривой , заданной уравнениями y y (t ) , z z (t ) аналогичная формула l t [ ; ] справедлива ( x ) 2 ( y ) 2 ( z ) 2 dt. b Если кривая AB задана уравнениям y f ( x) , x [a; b] , то l 1 ( f ( x)) 2 dx . a В случае задания плоской кривой в полярной системе координат ( ) , 1 2 , то её длина находится по формуле l 2 2 ( ) ( ( )) 2 d 1 Пример 7. Найти длину кривой x 2 y 2 2 x . В данном случае целесообразно перейти к заданию кривой в полярных координатах. Уравнение окружности имеет вид 2 cos . l 2 4 cos 2 4 sin 2 d 2 2 2 d 2 2 2 2 . 2 Замечание Уравнение x y 2 x или ( x 1) 2 y 2 1 задаёт окружность с центром в точке (1;0) и радиусом R=1. Известно, что длина окружности равна 2R . 2 2 Лабораторная работа № 4. Разложение функции в ряды Тейлора и Лорана. Всякая бесконечно дифференцируемая дробь в интервале x x0 r может быть единственным образом разложена в сходящийся ряд Тейлора из этого интервала ряд Тейлора с f ( x0 ) f ( x0 ) f ( n ) ( x0 ) f ( x) f ( x0 ) ( x x0 ) ( x x0 ) 2 ( x x0 ) n , если в этом 1! 2! n! ( n 1) f (c) интервале выполняется условие lim Rn ( x) lim ( x x0 ) n1 0 , где Rn (x) n n (n 1)! остаток ряда, c x0 ( x x0 ) , 0 1. На практике можно пользоваться следующей теоремой, которая даёт простое достаточное условие разложимости f (x) в ряд Тейлора. Теорема. Если модули всех производных функции f (x) ограничены в интервале x x0 r одним и тем же числом M 0 , то для любого x из этого интервала ряд Тейлора функции f (x) сходится к f (x) . f (0) f (0) 2 f ( n ) (0) n x x x , 1! 2! n! называемый рядом Маклорена. Приведём примеры разложения в ряд Маклорена некоторых элементарных функций. При x 0 получается ряд f ( x) f (0) x x2 xn x (;) 1! 2! n! x3 x5 x 2 n1 n sin x x (1) x (;) 3! 5! (2n 1)! x2 x4 x 2n cos x 1 (1) n x (;) 2! 4! (2n)! ( 1) 2 ( 1) ( n 1) n (1 x) 1 x x x , где 1! 2! n! [1;1], если 0, x (1;1], если 1 0, (1;1), если 1 ex 1 1 1 x x 2 x 3 x n , x (1;1) 1 x n 1 x2 x3 n x ln( 1 x) x (1) , x (1;1] 2 3 n 1 x3 x5 x 2 n 1 arctg x x (1) n , x [1;1] 3 5 2n 1 1 x 3 1 3 x 5 1 3 5 x 7 1 3 5 (2n 1) x 2n1 arcsin x x , x [1;1] 2 3 24 5 246 7 2 4 6 (2n) 2n 1 Для разложения f (x) в ряд Тейлора (Маклорена) нужно: 1) найти производные f ( x), f ( x),..., f ( n ) ( x), 2) сосчитать значения производных в точке x x0 (для ряда Маклорена в точке x 0 ), 3) написать ряд для заданной функции и найти его интервал сходимости, 4) найти интервал, в котором Rn ( x) 0 при n . Если такой интервал существует, то в нём сумма составленного ряда совпадает с функцией f (x) . 5) Лабораторная работа № 5. Вычисление значений функций с помощью степенных рядов. Для вычисления значения функции f (x) при x x1 с заданной точностью функцию в интервале ( R; R ) разлагают в степенной ряд f ( x) a0 a1 x a 2 x 2 a n x n , x1 ( R; R) . Точное значение f ( x1 ) равно сумме этого ряда при x x1 , а приближённое – частичной сумме S n ( x1 ) , т.е. f ( x1 ) S n ( x1 ) . Точность этого равенства увеличивается с ростом n, а абсолютная погрешность равна f ( x1 ) S n ( x1 ) rn ( x1 ) , где rn a n 1 x1n 1 a n 2 x1n 2 Таким образом, для оценки погрешности нужно оценить сумму отброшенных членов. Если данный ряд знакопостоянный, то составляют ряд из модулей членов ряда и для него стараются подобрать положительный ряд с большими членами, который легко бы суммировался. Обычно это бесконечно убывающая прогрессия. В качестве оценки rn ( x1 ) берут величину остатка этого нового ряда. В случае знакопеременного ряда, члены которого удовлетворяют признаку Лейбница, используется оценка rn ( x1 ) a n 1 x1n 1 . Оценку остатка ряда можно производить с помощью остаточного члена ряда Маклорена f ( n1) (c) , где 0 c x1 f ( x1 ) S n ( x1 ) rn ( x1 ) (n 1)! Пример 8. Вычислить число e с точностью до 0,001. 1 1 1 x x2 xn подставим x 1: e 1 В формулу e x 1 1! 2! n! 1! 2! n! Для нахождения числа e оставим n слагаемых и оценим ошибку rn (x) : rn ( x) 1 1 1 1 1 1 1 (n 1)! (n 2)! (n 3)! (n 1)! n 2 (n 2)( n 3) 1 1 1 . В квадратных скобках стоит бесконечно убывающая 1 2 (n 1)! n 1 (n 1) 1 1 прогрессия с знаменателем q , тогда сумма прогрессии равна . 1 n 1 1 n 1 1 1 1 1 n 1 1 Окончательно получаем , т.е. rn ( x) . 1 n!n (n 1)! (n 1)! n n!n 1 n 1 Подберём наименьшее натуральное число n, чтобы выполнялось неравенство Подбором убеждаемся, что это неравенство выполняется при n 6 , поэтому 1 1 1 1 1 1 e 1 2,718 1! 2! 3! 4! 5! 6! 1 0,001 . n!n Лабораторная работа № 5. Применение степенных рядов к вычислению определённых интегралов. Для приближённых вычислений неопределённых и определённых интегралов, в случае, когда первообразная не выражается через элементарные функции или её нахождение сложно, применяются степенные ряды. b Пусть требуется вычислить f ( x) dx с заданной точностью. Подынтегральную a функцию f (x) раскладываем в ряд по степеням x в интервале ( R; R ) , который включает в себя отрезок [a; b] . Для вычисления заданного интеграла можно воспользоваться теоремой о почленном интегрировании степенного ряда. Ошибка вычислений определяется так же, как и при вычислении функций. 1 4 Пример 9. Вычислить e x dx с точностью 0,001. 2 0 Решение. Разложим подынтегральную функцию в ряд Маклорена в интервале (;) 2 e x 1 x2 x4 x6 1! 2! 3! 1 Интегрируя обе части равенства на отрезке [0; ] , лежащем внутри интервала сходимости 4 1 1 1 2 4 6 3 5 7 4 4 4 2 x x x x x x (;) , получим e x dx 1 dx x 1 ! 2 ! 3 ! 1 ! 3 2 ! 5 3 ! 7 0 0 0 1 1 1 1 1 1 . Так как 0,0052 0,001 , а 0,001 , то 3 5 7 3 4 1!3 4 2!5 4 3!7 4 1!3 4 2!5 4 5 погрешность по модулю меньше первого отброшенного члена (ряд Маклорена 1 4 1 1 0,245 4 1!3 4 3 0 Лабораторная работа № 6. Применение степенных рядов к решению дифференциальных уравнений. В случаях, когда интегрирование дифференциального уравнения в элементарных функциях невозможно или способ его решения слишком сложен, решение такого Лейбнецкого типа). Получим e x dx 2 уравнения следует искать в виде ряда Тейлора y c n ( x x0 ) n .Коэффициенты ряда cn n 0 находят подстановкой ряда в уравнение и приравниванием коэффициентов при одинаковых степенях ( x x0 ) в обеих частях полученного равенства. Если удаётся найти все коэффициенты ряда, то полученный ряд служит решением во всей своей области сходимости. Этим способом можно интегрировать линейные дифференциальные уравнения с переменными коэффициентами. Пример 10. Решить задачу Коши для уравнения y xy y x cos x; y (0) 0, y (0) 1 . Сначала разложим правую часть в степенной ряд по степеням x, т.к. у нас x0 0. x2 x4 x cos x x 1 . 2! 4! Будем искать решение уравнения в виде ряда y c0 c1 x c 2 x 2 c3 x 3 c 4 x 4 . Тогда y c1 2c 2 x 3c3 x 2 4c 4 x 3 5c5 x 4 y 2c 2 6c3 x 12c 4 x 2 20c5 x 3 30c6 x 4 Из начальных условий находим c0 0, c1 1 . Подставим полученные ряды в исходное уравнение (2c 2 6c3 x 12c 4 x 2 20c5 x 3 30c6 x 4 ) x (c1 2c 2 x 3c3 x 2 4c 4 x 3 5c5 x 4 ) + x2 x4 x6 + (c0 c1 x c 2 x 2 c3 x 3 c 4 x 4 ) x 1 . 2! 4! 6! Приравниваем коэффициенты при одинаковых степенях x: 2c 2 0 x0 6c3 2 1 x1 x 2 12c 4 3c 2 0 x 3 20c5 4c3 1 2 ……………………. 1 1 1 Решая эту систему, находим: c2 c4 c6 c2 n 0 , c3 , c5 , c7 , 3! 5! 7! 3 5 7 x x x Получаем искомое решение в виде ряда y x или y sin x . 3! 5! 7!

