Статистический арбитраж

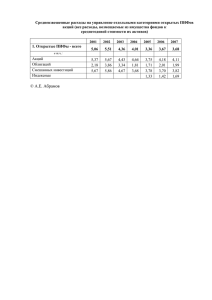
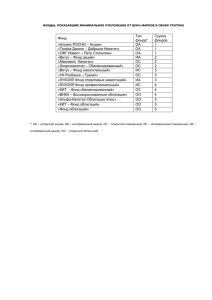
А.А.Эдилбаев
Научный руководитель Л.П.Петрова
(РЭУ им. Г.В. Плеханова)
СТАТИСТИЧЕСКИЙ АРБИТРАЖ.
Статистический арбитраж - это рыночно - нейтральная стратегия, которая в
теории приносит прибыль при любой ситуации на рынке. Сюда можно отнести парную
торговлю, когда трейдер делает предположение о синхронности движения
высококоррелированных активов. Акции компании одной отрасли должны, согласно
этой теории, реагировать одинаково на внешний фон, если он не затрагивает
непосредственно только одну из них. Динамика цен повторяет друг друга, а любое
отклонение от привычного паритета должно быть компенсировано одной или другой
акцией. Например, акции одной отрасли, цены фьючерсов и цены спот на товарных
рынках, валютные пары, акции компаний и их депозитарные расписки ит.д.
Проанализируем курсы акций российских компаний: Газпром, Роснефть,
Татнефть, Сургутнефтегаз, Лукойл и Норникель за период с 3 февраля 2010 года по 3
октября 2011 года. Наибольший коэффициент корреляции (0,83) наблюдается у пары
Газпром-Лукойл. Проведем некоторые преобразования рядов данных (нормирование,
центрирование и удаление тренда). Проделаем следующие шаги: прологарифмируем
ряды данных. Это позволит нам убрать квадратичный тренд, присущий акциям,
анализируемым на большом промежутке времени. Посчитаем среднее значение
логарифмов по каждому ряду и вычтем его из каждой цены. Таким образом, мы
проведем центрирование и, соответственно, уберем константу. Рассчитаем
среднеквадратическое отклонение цен и разделим на него центрированный ряд.
Проделаем эти операции со всеми рядами курсов акций из нашего списка. Для
дальнейшего анализа выберем пару Газпром – Лукойл.
Далее проведем тест на причинность по Грейнджеру. Построим два линейных
однофакторных уравнения вида G  a  L  b , L  c  G  d , где G – преобразованный курс
акций компании Газпром, L – преобразованный курс акций компании Лукойл.
Gˆ  0,81956  L  8, 013  Е  14; Lˆ  0,81956  G  7, 416  Е  14;
t расч  31, 27;
t расч  31, 27;
t расч  tтабл  1,96.
t расч  tтабл  1,96.
Найдем ошибки каждой из моделей (е(t)).
Для ошибок оценим уравнение следующего вида:
(1)
e(t )  a  b  e(t  1) ,
где e(t )  e(t )  e(t  1).
Проверим статистическую значимость коэффициентов b при помощи критерия
Стьюдента:
 t расчетное = 2,8622 для параметра b (уравнения вида (1) для Газпрома),
поскольку расчетное значение по модулю превышает табличное (1,96), то параметр b
является статистически значимым;
 t расчетное =3,4857 для параметра b (уравнения вида (1)для Лукойла),
поскольку расчетное значение по модулю превышает табличное (1,96), то параметр b
является статистически значимым. Таким образом, с помощью теста Грейнджера
доказана коинтеграция двух рядов данных, а именно: преобразованного курса акций
Газпрома и преобразованного курса акций компании Лукойл. Полученные результаты
могут быть использованы при построении стабильной торговой системы.