лек

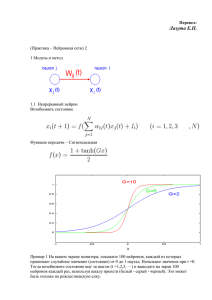
Лекция 5.
После того как было установлено, что можно решить только если будет выполняться
условие линейной разделимости был проведен анализ с целью выявления неких
оценочных объемов, примеры которых линейно неразделимы. Решение проблемы
линейной разделимости стало использование многослойных сетей. Например двухслойная
сеть может быть получена простым соединением двух однослойных сетей. И она будет
способна выполнить более широкий круг задач, чем однослойная. При этом отделяемые
точки должны содержаться в выпуклых областях. Область называется выпуклой, если для
любых точек из этой области, отрезок который их соединяет полностью лежит в этой
области.
Рассмотрим простую двухслойную сеть с двумя входами и одним выходом.
Рисунок
Пусть порог выходного нейрона = 0,75, а оба его веса v1=v2=0,5. в этом случае для того
чтобы порог был превышен и на выходе появилось 1 надо, чтобы оба нейрона были
активны. Таким образом реализация ф-ия-и аналогичным образом реализуются и более
сложные функции.
Самоорганизующаяся карта Кохонена
Одна из разновидностей нейросетевых алгоритмов. Основное отличие данной технологии
от рассмотренных ранее нейросетей является то, что обучение этой структуры происходит
на основании алгоритма обучения без учителя. Нейроновые сети данного типа
применяются для решения различных задач, начиная от прогнозирования до
восстановления пропуска данных. Алгоритм работы самоорганизующихся карт – один из
вариантов кластеризации многомерных векторов. Важным отличием алгоритма является
то, что в нем все нейроны (узлы, центры классов) упорядоченных в некоторую структуру.
При этом в ходе обучения модифицируется не только нейрон поб-ль, но и его соседи, но в
меньшей степени. За счет этого данный алгоритм так же относится к методам
проецирования многогмерного пространства в пространство с более низкой
размерностью. При использовании этого алгоритма векторы, которые были похожи и в
исходном пространстве оказываются рядом на получаемых картах. Нейрон- поб-ль –
нейрон, который в наибольшей степени соответствует входному вектору. Именно он и
определяет к какому классу относится пример и модифицируется при обучении. Данный
алгоритм подразумевает использование упорядоченной структуры нейронов, для этого
часто используется двухмерные сетки.каждый нейрон педставляет собой n-мерный
вектор-столбец. Формула , где n размерность исходного пространства. Обычно нейроны
располагаются в узлах двухмерной сетки с прямоугольными или шестиугольными
ячейками. При этом эти нейроны могут взаимодействовать друг с другом. Величина этого
взаимодействия определяется расстоянием между нейронами на карте. Количество
нейронов нашей сети определяется степенью детализации результатов работы. При
реализации алгоритма заранее задается непонятно и количество нейронов в сети. При
этом начальный радиус обучения в значительной степени влияет на способы карт сделать
обобщение. Радиус обучения непонятно который определяет скаолько нейронов кроме
нейрона побед. участвует в обучении (т е корректирует свои веса)на данной итерации.
Радиус обучения расст в пространстве векторов весов нейронов, т е любой нейрон карты,
расстояние от векторов весов которых до вектора весов нейронов- победителя меньше
радиуса обучения. Участвуют в коррекции весов на данной итерации. Радиус обучения
максимальный на первой итерации и уменьшается в дальнейшем по определенной
непонятно, так что в конце изменяет свой вес только нейрон- победитель. Если
количество узлов карты превышает количество примеров, то очень важно грамотно
выбрать радиус обучения. Непосредственно перед началом обучения проводят
инициализацию весов нейронов. Этот шаг достаточно сильно влияет на получение
качественных результатов. Инициализацию можно осуществить 4 способами.
1. инициализация случайных значений.
2. инициализация примерами, когда в качестве начальных значений задают
случайные значения из выборки.
3. линейная инициализация. Веса инициализируются значением векторов линейно
упорядоченных относительно линейного подпространства.
Обучение состоит из последовательности коррекции векторов (нейронов). На каждом
шаге обучения из исходного набора данных случайно выбирают один из векторов, а
затем производят поиск похожего на него вектора весовых коэффициентов.
Непонятное предложение. После этого происходит корректирование весов в сети.
Нейрон-победитель и его соседи сдвигаются в направлении вектора из исходного
множества. Данная процедура повторяется до тех пор, пока вектор из исходного
множества и вектор весов нейрона-победителя не совпадут. После окончания процесса
обучения для каждой переменной строится карта. На каждой карте при помощи
цветовой кодировки отмечаются примеры из исходного множества. Как правило
меньшим значениям соответствуют более холодные и наоборот. На каждой карте
отмечаются границы получившихся групп (кластеры). Полученные карты могут быть
использованы для других аналитических операций. Качество разбиения по каждому
разбиению оценивается визуально.
Процедурные системы
Это модуль вычислений, который обеспечивает управление процессом решения задачи
по образцу и состоит из набора продукц. правил (продукция) , раб памяти и цикла
управления – распознавание действия играет заметную роль в области ИИ при
решении задач поиска. Продукция – это пара условие-действие, которая определяет
одну порцию знаний, необходимых для решения задач. Условная часть правила – это
шаблон, который определяет, когда это правило может быть применено для решения
задачи на каком то этапе, определяет соответствующий шаг в решении задачи. Раб
память содержит описание текущего состояния пространства поиска в процессе
рассуждений. Это описание является образцом, которое сопоставляется с условной
частью правила, чтобы выбрать дальнейшее действие. При совпадении содержимого
раб памяти и условной части некоторого правила может выполняться действие,
связанное с этим условием. Действия правил направлены на изменение содержания
раб памяти. Распознавание-действие: управляющая структура продукц системы
действует следующим образом. Раб память инициализируется начальным описанием
задачи, текущее состояние решения задачи представляется набором образцов раб
памяти. Эти шаблоны сопоставляются с условием правил, что создает подмножество
правил вывода (какое то там множество) условия этих правил согласованы с шаблоном
из раб памяти и правила, которые содержаться в каком то там множестве называются
допустимыми. Выбирается и активируется одно из правил из данного множества,
активизация правила ведет к выполнению его действия, при этом содержимое раб
памяти изменится. После того как правило сработало, цикл повторился уже для
модифицированного состояния памяти. Процесс заканчивается когда содержимому
раб памяти не соответствуют никакие условия. В процессе разрешения конфликтов
необходимо выбрать для выполнения какое то правило и конфликтного множества.
Для этого используют различные способы от простого выбора первого попавшегося
правила до использования разнообразных сложных эвристик. Чистая продукционная
модель не имеет никаких механизмов для выхода из тупиковых состояний в процессе
поиска. Она продолжает работать пока не будут исчерпаны все имеющиеся правила.
Большинство практических реализаций продукц систем обладают вышеуказанными
механизмами.
1 – шаблон раб памяти
2. набор правил, если A1 то B1 , A2 то B2 , A3 то B3
25