Нейросетевые технологии наиболее успешно применяются при

Нейросетевые технологии наиболее успешно применяются при решении следующих задач:
1) распознавание образов;
2) задачи анализа;
3) в экономике: прогнозирование курсов акций, валют, цен, прогнозирование налоговых поступлений,
оценка стоимости недвижимости, оценка рисков (финансовых, кредитных);
4) банкротство фирм и банков.
Появилось много программных продуктов на основе НС. Примеры наиболее успешного применения
НС:
1) распознавание текста;
2) применение НС для исследования нервной системы человека (определение усталости военных
летчиков в реальном времени);
3) распознавание радарных, звуковых, видеосигналов в реальном времени;
4) прогнозирование результатов выборов;
5) оценка кредитных рисков.
Отличия нейрокомпьютеров от обычных
В простейшем варианте нейрокомпьютер – обычная ЭВМ со встроенной нейроплатой.
1) построение нейронного компьютера совершенно отлично от Фон-Неймановского;
2) высокая производительность за счет распараллеливания вычислений;
3) НС – быстрая самонастройка или обучение на решение конкретной задачи.
Нейрон как нервная клетка биологической системы
Нейрон – функционально самостоятельный аналоговый элемент.
Дендриты
Сома
(тело)
Аксон
Синапсы
Аксон (1 длинный отросток) – генерирует выходной импульс
Дендриты – входные сигналы (различают тормозящие и возбуждающие)
Когда число входных возбуждающих сигналов больше числа тормозящих на некоторый порог, аксон
формирует выходной импульс.
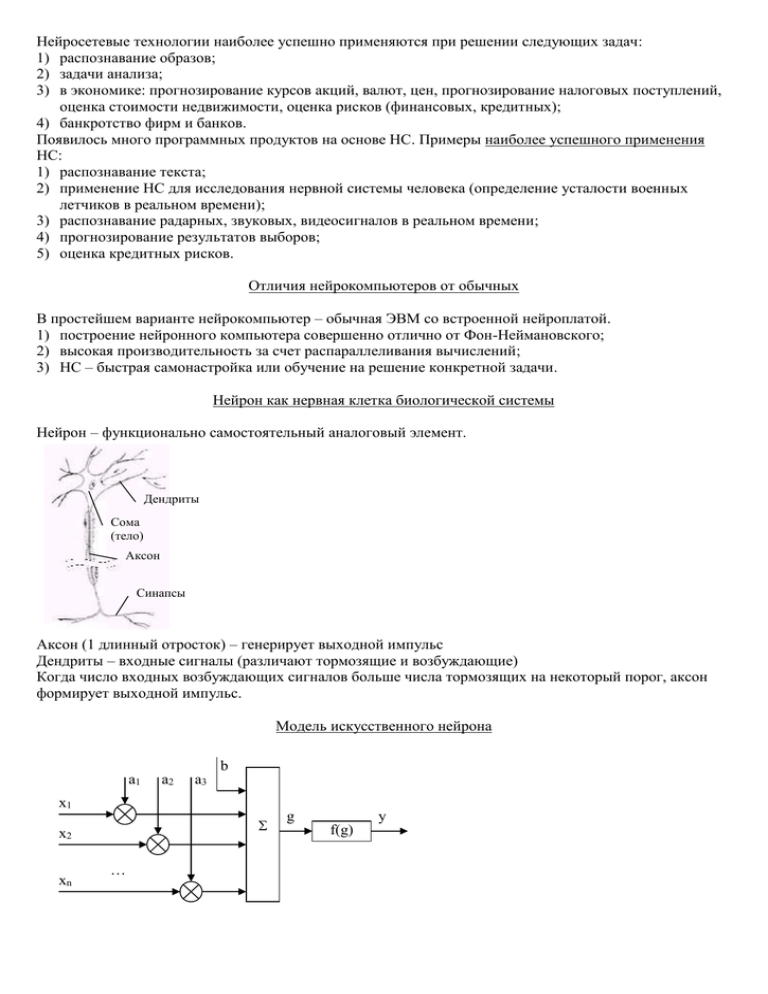
Модель искусственного нейрона
b
a1
a2
a3
x1

x2
xn
…
g
y
f(g)
 – сумматор
(X) – блок умножения
b – смещение
a1,a2 … an – коэффициенты умножения
x1,x2 … xn – входные сигналы
y 
 N


f 
a
x

b
i
i


 i 1

где x – вектор входных сигналов;
a – вектор весовых коэффициентов (a  0) – определяет пропускную способность канала;
N – размерность выходного сигнала;
b – смещение (пороговое значение);
f(g) – функция активации нейрона (как правило – нелинейная, очень важный элемент нейрона).
Примеры функций активации
f
0
1. y = f(g) = k*g
g
2. y = f(g) = sign(g)
f
0
-1
1
g
3. y = f(g) = 1 / (1+e–g)
f
0
1
g
Нейросети
Из отдельных нейронов можно построить отдельный слой нейросети. Слой – совокупность нейронов,
имеющих единый входной сигнал, а сами нейроны не связаны между собой.
слой
 N

y j  f j   aij xi  b j 
 i 1

yj – выходной сигнал
N – число нейронов в слое
xi – вектор входного сигнала
aij – матрица весовых коэффициентов
Из слоев можно строить многослойную сеть
y kjk

f jkk
 Nk k k
  ai j xi  b kj
k
 i 1 k k k
k




k – номер слоя
Nk – число нейронов в k-м слое
Перекрестные
связи
X
1
2
2
1 Y X
2 Y
слой
слой
k
… X
k
слой
Y
Обратные
связи
Если k – слой, который формирует сигнал; k+s – слой, на который сигнал поступает, то связи:
– последовательные (s = 1)
– обратные (s < 1)
– перекрестные (s > 1)
Однородная НС – это сеть, у которой функция активации в пределах одного слоя одинакова.
Такт работы НС – будем считать промежуток времени, измеряемый с момента подачи входного сигнала
до момент получения выходного сигнала.
НС может быть реализована:
– на микросхемах:
а) цифровых;
б) аналоговых;
– на световых элементах;
– программно.
Нейронный алгоритм решения задачи
НА (нейроалгоритм) – вычислительная процедура, основная часть которой реализуется на НС.
Обязательные элементы НА:
1) объекты, выступающие в роли входного сигнала НС (X);
2) объекты, выступающие в роли выходного сигнала НС (Y);
3) желаемый (требуемый) выходной сигнал (Y с чертой)
4) структура нейросети:
– кол-во слоев;
– связи;
– объекты, выступающие в роли весовых коэффициентов НС;
5) функция ошибки НС: f(Y с чертой – Y);
6) критерий качества обучения (функционирования НС);
7) определение значений весовых коэффициентов – могут вычисляться следующими способами:
– по аналитическим формулам (явно);
– численными методами из решения неявной (нелинейной) задачи;
– с применением процедуры настройки (обучения).
Определим нейроалгоритм, можно решать задачу на нейрокомпьютере.
Нейроалгоритм решения систем линейных неравенств
a11 x1  a12 x2  ...  a1n xn  b1
a x  a
 21 1
22 x2  ...  a 2 n xn  b2

...

a m1 x1  am 2 x2  ...  amn xn  bm
AXB
Построим нейроалгоритм:
1) входным сигналом НС будем вектор X
X = [x1, x2, … xn], X0 = [0]
2) выходной сигнал НС – вектор Y
Y = [y1, y2, … ym], yi –характеризует разницу между левой и правой частью неравенства
3) желаемое значение – примем равным нулю
Y с чертой = [0, 0 … 0]
4) структура НС – достаточно построить 1 слой НС, поскольку вид уравнения однослойной НС: Y=f(g);
g=g(A,B,X); где f – функция активации, g – разница между левой и правой частями.
g=AX–B0; Y=f(AX–B)
Из этого следует, что НС фактически вычисляет левые части неравенств:
AX–B0
Весовыми коэффициентами являются коэффициенты матрицы A, а вектором смещения –
коэффициенты правой части B. Сеть получается однородной.
–B
A
X

g
f(g)
Y
Функция активации должна активизировать следующее:
0, g  0;
f g   
 0, g  0.
Поэтому ее можно записать так:
0, g i  0;
f gi   
 g i , g i  0.
i=1..m
f
0
g
5) Функция ошибки НС – определим ее как разность:
Е=Y – Y с чертой
но т.к. Y с чертой=0, то E=Y
Вычисление E производится в блоке вычисления ошибки:
Y
E
Y
6) Критерий качества системы: будем оптимизировать функционал:
m
F   ei2
i 1
E = [e1,e2, … em]
F – сумма квадратов отклонения ошибки, тогда процедура настройки НС сводится к решению
оптимизационной задачи:
F (E)  min
Причем настраиваются не весовые коэффициенты НС (они известны), а компоненты искомого вектора
X. Таким образом, эту оптимизационную задачу можно решить следующим способом:
A
-B
Y
Y
E
НС
Блок ошибок
X(0
T
A
H
B
)
+
x
Блок обучения
T – линия задержки;
Благодаря обратной связи находится решение оптимизационной задачи (за какое-то число тактов
работы нейросети) поиска min с помощью итерационного градиентного метода:
X(k+1)=X(k)–X(k)
k – номер итерации
Можно синтезировать блок настройки:
X
(k )
F
H
x
T

xx
(k )
 F F
F 

 H 
,
,...,
xn 
 x1 x2
T
 F 
 x 
 1
 H ... 
 F 


 xn 
где:
F – функция
X – вектор
H – коэффициент усиления
Найдем градиент критерия, примем во внимание, что:
m

F   yi  y i

i 1
n
yi   aij x j  bi
j 1
поэтому :
F
 2 Y T  A
x
F
отсюда :
 2  AT  Y
x
T
Вид нейроалгоритма:
X ( 0)  X нач.  0
Y ( k )  f ( AX ( k )  B)
X ( k 1)  X ( k )  2 HAT Y ( k )
Закончить итерации, когда E  0
Динамическая система:
нейронная сеть
g
AX–B
X
Y  0
f (g)
Y
–
E
A, B
X(0)
блок настройки
–2H
AT
T
X(k)
+
X(k)
блок
ошибки
Нейроалгоритм решения систем линейных уравнений
Пусть дана система линейных уравнений:
AX=B
Построим нейроалгоритм, определяющий с заданной точностью для любой матрицы A (вещественной,
невырожденной, порядка N), вектора B, некоторое значение X, при котором система уравнений
обращается в тождество.
Нейроалгоритм:
1) входной сигнал НС – X;
2) выходной сигнал – Y;
3) желаемое значение – Y с чертой = [0]
4) сигнал ошибки – E
5) структура НС определяется аналогично решению систем линейных неравенств
6) функция активации – можно выбирать различными способами. Для удобства взятия производной
возьмем ее в виде:
f
0,    g i  
f gi   
 g i , иначе.
0
g
–e +e
Значение E является параметром и выбирается из необходимой точности вычисления корней.
–B
A
X
g

f(g)
Y
НС – однослойная, однородная; весовые коэффициенты – A; вектор смещения – (–B). Полученная НС –
с настройкой входного сигнала (настройку осуществляется блок настройки, расположенный в обратной
связи).
Итерационная градиентная процедура для минимизации функции ошибки:
N
F  E  E   ei2  min
T
i 1
x
Реализуется на такой же общей схеме, которая применяется для систем линейных неравенств.
Нейроалгоритм решения систем линейных неравенств:
X ( 0)  X нач.  0
Y ( k )  f ( AX ( k )  B)
X ( k 1)  X ( k )  2 HAT Y ( k )
Закончить итерации, когда E  0
Решение на НС задачи линейного программирования
Математическая постановка задачи:
N
А   сi xi  min
i 1
a11 x1  a12 x2  ...  a1n xn  b1
a x  a x  ...  a x  b
 21 1 22 2
2n n
2

...
am1 x1  am 2 x2  ...  amn xn  bm
xi  0, i  1, n
В матричной форме:
C T  X  min
A X  B
где
A – матрица m X n
B – вектор m X 1
X – вектор n X 1
С – вектор n X 1
Разработка НА
1) входной сигнал НС: X – вектор неизвестных;
2) выходной сигнал НС: Y – вектор с числом компонент, равным числу ограничений (неравенств);
3) желаемое значение: Y с чертой – вектор (нулевой);
4) сигнал ошибки: E = Y – Y с чертой = Y
5) структура НС: такая же, как для решения систем линейных неравенств и систем линейных
уравнений – однослойная однородная, с матрицей весовых коэффициентов A и вектором смещения
B, Y=f(g), g=g(A,B,X);
6) функция активации: “ступенька”
f
0, g i  0
1
f gi   
1, g i  0.
0 g
7) построение градиентной итерационной процедуры:
функция цели: возьмем следующий функционал для минимизации:
m
n
i 1
i 1
F   ei   D   ci xi  min
x
где ei – компонент вектора ошибки E
D некоторый параметр – константа, подбирается индивидуально, субъективно (определяет степень
влияния функции цели).
Получим алгоритм:
X ( 0)  X нач.
Y ( k )  f ( AX ( k )  B)

X ( k 1)  X ( k )  H AT Y ( k )  D  C

Момент окончания определяется таким образом, чтобы обеспечивалось Y=[0] – выполнение неравенств.
Структура динамической системы:
A
B
Y
Y
g
AX–B
X(0
)
E
T
-H
x
X
D
X
C
AT
ATY
Сортировка на нейросети
Сортировка – одна из наиболее распространенных задач – занимает много времени. Пусть дано
множество чисел: xi, i=1..n.
Необходимо упорядочить это множество по возрастанию:
xi , i  1, n,
ji : y j  xi
и
y j 1  y j : j  1, n
Есть несколько подходов к построению нейроалгоритма. Рассмотрим один из них:
Алгоритм сортировки для НС с настройкой (ручной) весовых коэффициентов:
Сортирующая
система
X
3
7
11
5
2
Y–№
2–2
3–4
5–5
7–3
11 – 1
Нейроалгоритм:
1) входной сигнал НС: последовательности исходных чисел xi;
2) выходной сигнал НС: при данной постановке им может быть n-мерный вектор целых чисел
yi  [1,n], указывающий номер числа xi в упорядоченной последовательности, т.е. его индекс;
3) желаемый выходной сигнал: по i-й координате представляет собой число неотрицательных значений
разностей (xi – xj) в i-й строке матрицы || xi – xj ||.
3   0  4  8  2
7   4
0 4 2
  
11   8
4
0
6
  
5   2  2  6 0
2   1  5  9  3
1   2
5 4

9  5 
  
3 3 
0 1 
С учетом такого определения желаемого выходного сигнала можно утверждать, что система сортировки
может быть построена без контура адаптации и вычисления ошибки в виде 2-х слойной НС с
фиксированными коэффициентами, реализующей следующую передаточную функцию:
yi   signxi  x j 
n
j 1
где:
1, если g  0
signg   
0, если g  0
4) Структура НС:
-1
x1
1
1

sign

sign
-1
x2
1
1
 y1
…
-1
xn
1

1
sign
…
-1
x1
1
1

sign

sign
-1
x2
xn
1
1
…
-1

1
 yn
1
sign
Первый слой состоит из n2 нейронов, каждый с 2-мя входами и коэффициентами (–1, 1). Второй слой –
состоит из n нейронов (линейных сумматоров) с n входами и единичными весами.
Можно уменьшить аппаратные затраты: после несложной модификации размер 1-го слоя сети можно
уменьшить в 2 раза (используя симметрию матрицы), а также можно убрать главную диагональ, а
добавить 1 единичный вход к каждому нейрону второго слоя.
Более того, если добавить еще один слой к этой сети, то можно получить алгоритм определения
минимального и (или) максимального элемента массива.
Однослойные и многослойные нейросети
Простая однослойная сеть
x1
a11
1
a12
x2
2
…
y1
y2
…
xm
n
yn
amn
A – матрица весовых коэффициентов (m x n), вычисление выходного вектора Y сводится к матричному
умножению Y=XA.
Многослойные сети строятся путем каскадного соединения отдельных слоев
x1
a11
a12
1
y1
2
2
y2
…
…
n
k
1
x2
…
xm
amn
b11
b12
yk
bnk
Вычисление выхода (если отсутствует нелинейная функция активации) сводится к матричным
операциям: Y=(xA)B, где A,B – матрицы весовых коэффициентов. Так как умножение матриц
ассоциативно, то: Y=x(AB), т.е. любая линейная нейросеть может быть приведена к эквивалентной
однослойной сети. Поэтому для увеличения возможностей сетей необходима нелинейная функция
активации.
Стратегии обучения нейросети
Цель: настроить сеть так, чтобы для некоторого множества входов давать желаемое (или, по крайней
мере, сообразное с ним) множество выходов. Обучение осуществляется путем последовательного
предъявления входных векторов с одновременной подстройкой весов в соответствии с определенной
процедурой. Существуют 2 стратегии обучения.
Обучение с учителем
Стратегия обучения с учителем предполагает, что для каждого входного вектора существует целевой
(желаемый) вектор. Вместе они образуют обучающую пару:
x, y 
Обычно нейросеть обучается на некотором числе таких обучающих пар, которое составляет обучающее
множество.
X
Нейросеть
Y
Y
–
Y
Алгоритм
обучения
Векторы обучающего множества предъявляются последовательно, пока ошибка настройки по всему
обучающему множеству не достигнет приемлемо низкого уровня.
Обучение без учителя
Стратегия “обучение с учителем” критикуется за свою биологическую неправдоподобность: в мозге не
существует механизма, который бы сравнивал желаемые и действительные значения выходов.
Обучение без учителя предполагает наличие только входных векторов. Обучающий алгоритм при
реализации стратегии “обучение без учителя” подстраивает веса нейросети так, чтобы предъявление
достаточно близких входных векторов давало одинаковые выходы. Процесс обучения группирует
сходные вектора в классы. После обучения предъявление на вход вектора из данного класса даст
определенный выходной вектор, но до обучения невозможно предсказать, какой выход будет
формироваться данным классом входных векторов. Выходы такой сети должны интерпретироваться в
некоторую понятную форму.
Представимость и обучаемость сети
Рассмотрим эти понятия на персептронах, у которых функция активации – пороговая. Ф.Розенблатт
доказал теорему, которая утверждала, что персептрон способен научиться всему, что он способен
представлять. Надо различать следующие два понятия: представляемость и обучаемость.
Понятие представляемости относится к способности персептрона (или другой сети) моделировать
определенную функцию.
Обучаемость же требует наличия некоторой процедуры настройки весов сети для реализации этой
функции.
Рассмотрим возможность построения НС, способной распознавать четные и нечетные арабские цифры.
Представима ли такая система распознавания персептроном? То есть можно ли сконструировать
персептрон и настроить его веса (неважно каким образом), чтобы он обладал такой разделяющей
способностью. Если это так, то говорят, что персептрон способен представлять желаемую машину
распознавания. К сожалению, не формального метода доказуемости представимости для НС.
Проблема функции “исключающее или”
Возможности представления однослойного персептрона весьма ограничены. М.Минский показал, что
однослойный персептрон не может даже воспроизвести такую простую функцию, как “исключающее
или”.
x1  x2 = y
точки
0
0
0
A0
0
1
1
B0
1
0
1
B1
1
1
0
A1
x1
x2
a1

f
g
y
a2
1, g  0,5
F g   
0, g  0,5
F(g)
1
0
0,5
g
Нейрон выполняет следующее вычисление:
g=a1x1+a2x2
Анализ показывает, что никакая комбинация значений весов a1 и a2 не может обеспечить соотношение в
таблице истинности функции.
Покажем это графически:
x2
A1
B1
x1
A0
B0
По одну сторону прямой y=0, а по другую – y=1. Изменяя значения a1 и a2 мы может только изменить
наклон прямой и ее положение. Чтобы персептрон реализовывал функцию нужно расположить
функцию так, чтобы точки A были с одной стороны, а точки B – с другой стороны.
Этот пример не единственный. О таких примерах говорят, что он линейно неразделимый. В случае 3-х
входов разделение осуществляется плоскостью, рассекающей 3-х мерное пространство. К сожалению,
не существует простого способа определить линейную разделимость функции, если еще и число
переменных велико. Поэтому применение однослойных персептронов ограничено. Добавив
дополнительные слои, можно устранить недостаток однослойного персептрона. Многослойная сеть
способна воссоздавать сложные выпуклые разделяющие области.
Рассмотрим двухслойную сеть с двумя входами:
x1
1
x1
b1
y
3
x2
2
x2
b2
слой 2
слой 1
Пусть: b1=b2=0,5; порог: 0,75; тогда нейрон (3) 2-го слоя реализует функцию “и”, а каждый нейрон 1-го
слоя реализует прямую линию.
B1
x2
A1
A0
B0
x1
Нейрон (3) принимает значение “1” только в области между прямыми. Добавляя нейроны в слой №1,
можно получить более сложные области. Трехслойная сеть позволяет строить классифицирующие
поверхности не только выпуклые.
Обучение персептрона
Рассмотрим пример обучения персептрона способности распознавать четные и нечетные цифры.
Входной образ цифры проецируется на некоторую панель, разбитую на квадраты (пиксели). От каждого
такого квадрата подается сигнал 0 или 1. При подаче на вход “правильного” образа на выходе
появляется сигнал 1. При подаче на вход “неправильного” образа на выходе появляется сигнал 0.
a1
a2
2

…
f
a
n
Пусть вектор X является двоичным образом распознаваемой цифры, тогда каждая компонента вектора
X(x1, x2, … xN) умножается на соответствующую компоненту вектора весов A. Если сумма
произведений X на A превышает порог , то выход нейрона Y равен 1 (лампочка горит), иначе выход –
0. Такую зависимость выхода от суммы входов реализуется функция активации нейрона f “ступенька”
f (g)
1
1, g  
0

g
f 
0,
g 
Для обучения сети образ X подается на вход и вычисляется выход Y. Если Y – правилен, то ничего не
меняется. Однако, если выход неправилен, что веса, присоединенные к входам, усиливающим
ошибочный результат, модифицируются, чтобы уменьшить ошибку. Например, если при четной цифре
лампочка горит – веса надо уменьшить. При нечетной цифре лампочка не горит – веса увеличиваем.
Метод обучения может быть следующим:
Начало
Подать
очередной
образ
Вычислить Y
Выход
правилен?
да
нет
значение
Y
Вычесть каждый
вход из соотв-го
веса
Добавить входы к
соответствующим
весам
За конечное число шагов сеть научится разделять цифры на четные и нечетные (если множество
образов линейно разделимо).
Алгоритм обучения по дельта-правилу
Это более общий метод обучения персептрона, он переносится и не непрерывные входы и выходы.
В начале обучения вычисляется ( = Y с чертой – Y).
Y с чертой – целевой выход
Y – реальный выход
Наличие целевого выхода означает, что данный метод реализует стратегию обучения с учителем.
Случай  = 0 – соответствует ветви “да”
Случай  > 0 – соответствует ветви “=0”
Случай  < 0 – соответствует ветви “=1”
Величина корректировки весов должна зависеть от следующих параметров:
i=  xi
где  – коэффициент “скорости обучения”
ai(k+1) = ai(k) + i
где i – коррекция по i-му входу
ai(k+1) – значение веса i после коррекции (на k+1 шаге)
Проблемы обучения персептрона
1. Трудность проверки выполнения условия разделимости для конкретного обучающего множества.
2. Входы часто меняются во времени и могут быть разделимы в момент времени t и неразделимы в
следующий t+1.
3. Алгоритм ничего не говорит о необходимом числе шагов обучения.
Обучение многослойной сети методом обратного распространения ошибки
История алгоритма обратного распространения (back propagation):
1974 – первое описание метода
1982 – раннее описание алгоритма
1986 – полное описание алгоритма
Рассмотрим данный метод на примере двухслойной сети:
x1
b11
b12
1
x2
…
xl
a11
a12
1
y1
ошибка 1
2
2
…
…
m
n
blm
y1
y2
y2
ошибка 2
yn
amn
yn
ошибка n
Трехслойная нейросеть
Слой №1
Слой №2
входной
вектор X
Слой №3
выходной
вектор Y
скрытые слои
Функция активации:
“Сигмоида”:
y = f(g) = 1 / (1+e–g)
f
1
0,5
g
0
Достоинства “сигмоиды”
1) простая производная: dy/dg = y*(1-y)
2) функция нелинейная (хорошая представимость);
3) автоматический контроль усиления сигнала (при маленьких g – функция усиливает слабые сигналы,
большие g – ослабляются – за счет насыщения сигмоиды).
Стратегия обучения – “обучение с учителем”
Типовые шаги:
1) выбрать очередную обучающую пару (X,Y с чертой) из обучающего множества и подать входной
вектор X на вход нейросети;
2) вычислить выход сети Y;
3) вычислить отклонение  = Y – Y с чертой;
4) подкорректировать веса сети так, чтобы минимизировать ошибку   min;
5) повторить шаги 1-4.
Шаги 1-2 – проход по сети в прямом направлении; для каждого слоя, начиная с первого, вычисляется Y:
Y=F(x*A), где A – матрица весов слоя, F – функция активации. Вычисление – слой за слоем.
Шаги 3-4 – проход по сети в обратном направлении; выполняется подстройка весов выходного слоя.
Для этого применяется модифицированное дельта-правило:
p
y pj a kpq
слой j
q
y qk
yq
Eq
слой k
На рисунке показан процесс обучения одного веса apqk от нейрона p в скрытом слое j к нейрону q в
выходном слое k. Для выходного нейрона q сначала находится сигнал ошибки:
Eq = yq с чертой – yqk
Он умножается на производную сжимающей функции [y(1–y)], вычисленную для этого нейрона слоя k.
Получаем величину :
q = yq(1–yq)Eq
Далее как в обычном дельта-правиле:
apqk =  qk ypj
где  – коэффициент скорости обучения (0,01   < 1).
ypj – выходной сигнал нейрона p слоя j.
apqk(t+1) = apqk(t) + apqk
apqk(t), apqk(t+1) – величина веса в связке нейронов pq на шаге t (до коррекции) и на шаге t+1 (после
коррекции).
Процедуру коррекции можно изобразить следующей функциональной схемой:
слой j
слой k
p
y pj a kpq
q
yq
y qk
Eq
F’

a kpq t  1
a kpq t 
Функциональная схема включает в себя операции умножения и сложения, следовательно процедура
обучения может быть реализована аппаратно в нейросетевом базисе.
Подстройка весов скрытого слоя:
Рассмотрим один нейрон скрытого слоя p. Для нейронов скрытых слоев неизвестен желаемый выходной
сигнал. Поступают следующим образом: при проходе вперед этот нейрон передает свой выходной
сигнал нейронам выходного слоя через соединяющие их веса. Во время обучения эти веса
функционируют в обратном направлении, пропуская величину  от выхода назад к скрытому слою.
предварительный
слой i
s
y si
скрытый
слой j
выходной
слой
a kp1  1k
p
a kp 2
 2k
a kpn
bspj
 nk

1
2
n

 pj  y pj 1  y pj   qk a kpq 


q
bspj    pj ysi
bspj t  1  bspj t   bspj
Ускорение процесса обучения:
1. Метод импульса
a kpq t  1   qk y pj  1 a kpq t 
где 1 – коэффициент импульса 1 = 0,9
Далее как в обычном дельта-правиле.
2. Метод экспоненциального сглаживания
a kpq t  1   a kpq t   1    qk y pj
где  – коэффициент сглаживания 0 <  < 1
Прогнозирование с помощью нейронной сети
Прогнозирование – это задача анализа временного ряда. Это одно из важных приложений нейросетей.
Задача анализа временных рядов заключается в том, чтобы получить будущее значение некоторой
величины, зная ее текущее и прошлые значения и располагая данными о среде.
Временной ряд – это упорядоченная последовательность вещественных чисел xt, t=1,2,3 … T,
представляющих собой результаты наблюдений некоторой величины. Эти значения обычно получают
как результаты измерений в некоторой физической системе.
Метод окон (для решения задачи анализа временного ряда)
Метод выявления закономерности во временном ряде на основе нейросети называется “Windowing”
(метод окон). Основная идея заключается в использовании двух окон: WI (Input – вход) и WO (Output –
выход) фиксированных размеров n и m соответственно, для наблюдения множества данных.
Эти окна способны перемещаться с некоторым шагом S по кривой (временному ряду) вдоль оси
времени. В результате получается некоторая последовательность наблюдений:
WI0, WI1 … WIN
(1)
O
O
O
W 0, W 1 … W N
(2)
функция
O
WIjWI
WOW j+1
j+1
0
j
время
Предполагается, что последовательность (1) однозначно отображается в последовательность (2) и эта
связь (в общем известная) определена на всем множестве данных. Первое окно WIj, сканировав такие
данные, передает их на вход нейросети, а второе WOj – на выход. Получающаяся на каждом шаге пара
WIj  WOj образует обучающую пару (наблюдение): { WIj , WOj }.
Рассмотрим пример:
Пусть имеется ряд (k=8)
1, 1, 2, 3, 5, 8, 13, 21
Зададим размеры окон: WI = 3, WO = 1, S = 1 (S – шаг перемещения)
С помощью метода окон будет получено следующее обучающее множество для нейросети:
1, 1, 2  3
1, 2, 3  5
2, 3, 5  8
3, 5, 8  13
5, 8, 13  21
Во временном ряде предполагается существование зависимостей, хотя и скрытых и нейросеть,
обучаясь, пытается извлечь эти закономерности и сформировать требуемую функцию прогноза. Если
ряд совершенно случайный, то прогнозировать ее трудно.
Различают два вида прогнозирования:
– одношаговое;
– многошаговое.
Многошаговое прогнозирование
Применяется для долгосрочного прогноза и имеет целью определение основного тренда для некоторого
фиксированного промежутка времени в будущем. Для прогнозирования система используется
полученные (выходные) данные для моментов времени T+1, T+2 …
В нашем примере для последующего использования в качестве выходных данных:
T+1: 8, 13, 21  38
T+2: 13, 21, 38  63
Одношаговое прогнозирование
Для конкретного прогноза (на один шаг) используется реальное, а не прогнозируемое значение для
осуществления прогноза на следующем шаге:
T+1: 8, 13, 21  38 (должно быть 34)
T+2: 13, 21, 34  63 (должно быть 55)
Общая схема финансового прогнозирования
Типичная последовательность:
Сбор данных
Архивация
данных
Фильтрация
данных
Выбор
показателей
НС
Доводка сети
Сценарии
торговых
операций
Торговля
Предварительная обработка:
Сбор данных – выбор совокупности переменных для описания моделируемого процесса. Проверка
значимости переменных (корреляционный анализ): реальные данные могут содержать шумы, их надо
очистить. Возможно масштабирование входных и выходных данных.
Сценарии:
Интерпретация выходной информации сети – м.б., надо подать ее на вход какой-то другой системы
поддержки принятия решений.
Кроме прогнозирования, нейронная сеть широко применяется в задачах классификации.
Применение экспертных систем в экономике
В экономике имеется много задач, которые не имеют строгого математического описания. Поэтому
целесообразно рассмотреть подходы, основанные на знании. В настоящее время создано много
интеллектуальных систем для решения этих задач. Накоплен большой опыт их применения,
сформировалась технология разработки этих систем. Появились инструментальные средства разработки
экспертных систем.
Первые экспертные системы:
MYCIN – медицинская экспертная система
PROSPECTOR – для геологов: прогнозирование залежей полезных ископаемых
DENDRAL – для анализа новых химических элементов
Рынок коммерческих СИИ:
1994 г. – 0,9 млрд. долл.
США – 0,6 млрд. долл.
Экспертные системы – 62%
Естественно-языковые системы – 12%
Нейронные сети – 26%
Кроме того, сейчас появилось много пакетов, использующих аппарат нечеткой логики. Наиболее
известной инструментальной системой для построения экспертных систем является G2. Имеет ряд
дополнительных пакетов, обеспечивающих использование нейронных сетей, нечеткой логики. Главным
достоинством является построение динамических экспертных систем, т.е. систем, позволяющих решать
задачи в реальном времени.
Причины, приведшие СИИ к коммерческому успеху
1. Интегрированность с другими технологиями (CASE, СУБД);
2. Открытость и переносимость (соблюдение стандартов) – разрабатываются с соблюдение
общепринятых стандартов;
3. Использование традиционных языков программирования и рабочих станций;
4. Архитектура клиент/сервер – поддерживается распределенный принцип обработки информации;
5. Предметная ориентация СИИ (крен в разработку прикладных СИИ).
Инженерия знаний
Это одно из направлений ИИ, в рамках которого рассматриваются все вопросы, связанные с
извлечением, приобретением и представлением знаний. Проблема автоматизации получения знаний в
настоящее время полностью не решена. Знание – это совокупность сведений, образующих целостное
описание, соответствующее некоторому уровню осведомленности о проблеме, задаче.
Отличия знаний от данных
Данные имеют следующие характеристики:
1) неинтерпретируемость – глядя на данные, нельзя сказать, какая решается задача, данные
интерпретируются только программой;
2) пассивность – логика решаемой задачи сосредоточена в программе;
3) изолированность – связь между данными определяется программой.
Знаниям свойственно следующее:
1) интепретируемость;
2) сложная логика из программы перемещается в базу знаний;
3) неизолированность понятий;
4) структурированность понятий – знания, как правило, иерархичны;
5) декларированность и процедуральность;
6) активность знаний (небольшие изменения в знаниях приводят к значительным корректировкам в
базе знаний).
Источники знаний
–
–
–
текст (инструкции, документы, книги, фотографии, рисунки и т.п.);
наблюдение;
специалист-профессионал.
В знания входят:
– факты, относящиеся к предметной области;
– закономерности;
– гипотезы о возможных связях между явлениями;
– процедуры решения типовых задач;
– средства, используемые экспертом.
Стратегии получения знаний
Получение и структурирование знаний осуществляется в соответствии с определенными этапами
разработки экспертных систем:
Идентификация
проблемы
Получение
знаний
Без применения
ЭВМ
Извлечение
знаний
Структурирование
С применением
ЭВМ
Приобретение
знаний
Формирование
знаний
Методы извлечения знаний
Извлечение знаний
Коммуникативные
методы
Пассивные
наблюдение
лекции
Текстологические
методы
Активные
анкетирование
интервью
диалог
анализ учебников
анализ
литературы
анализ
документов
“мозговой штурм”
круглый стол
Все методы неформальны, субъективны и присутствуют в виде определенных рекомендаций.
Методы приобретения знаний
1.
–
–
–
2.
3.
4.
Прямые методы
структурированное интервью;
методы когнитивной (познавательной) психологии;
диагностический игры;
Приобретение знаний из примеров
Приобретение знаний из текста
Приобретение знаний из БД
Прямое приобретение знаний (метод репертуарных решеток)
История: в 1955 г. Дж. Келли (врач-психотерапевт) создал теорию личности и на ее основе разработал
методику ее практического применения – технику “репертуарных решеток”. Стратегия репертуарных
решеток направлена на преодоление когнитивной защиты эксперта. Она позволяет изучить систему
личных (личностных) конструктов другого человека. Сознание состоит из конструктов. Конструкт – это
биполярная ось.
Холод
Тепло
Сильный
Слабый
Выявление множества конструктов – это и есть преодоление когнитивной защиты. Каждая шкала – это
два оппозиционных свойства. Наиболее эффективный способ выявления оппозитных свойств – метод
триад, представляющий собой структурированное интервью. Эксперту предъявляется три семантически
связных события (понятия) с предложением назвать свойство, отличающее одно событие от двух
других.
Пример:
Эксперту в языках программирования предъявляется триада понятий: Паскаль, Ассемблер, Си.
Эксперту предлагается ответить на вопросы:
1. Какой язык отличается от двух других?
Ответ: Ассемблер
2. Какое свойство отличает Ассемблер от Паскаля и Си?
Ответ: Язык низкого уровня
3. Назовите оппозитной свойство свойству “Язык низкого уровня”?
Ответ: Язык высокого уровня
4. Дайте имя свойству, имеющему значения “низкий уровень программирования”, “высокий уровень
программирования”?
Ответ: Уровень программирования.
В результате формируется в репертуарной решетке шкала “уровень программирования”.
Система
приобретения
Эксперт
БЗ
знаний
Репертуарная решетка:
Языки
Имя
Значение
свойства
Паскаль Асм. Си
Уровень
Низкий
10
1
3
прогр-я
Тип
Процеязыка дурный
…
Пролог
10
Значение
Высокий
Объектный
…
В результате можно выявить другие свойства объектов предметной области. Этот процесс
продолжается, пока не происходит насыщение. Так выявляются элементы множества личностных
конструктов конкретного эксперта. Формируется базис свойств предметной области.
Получение каузальных знаний: строится конъюнктивная проекция на шкалы:
“Что такое язык Ассемблер?”
низкий
уровень
1
2
3
4 5
высокий
уровень
структури
рованный
1
2
3
4 5
не структурированный
2
3
4 5
плохой
доступ к
1
системным
средствам
ЭВМ
хороший
доступ к
системным
средствам
ЭВМ
Продукционное правило:
Если уровень программирование = низкий и стиль программы = не очень структурированный и доступ
к системным средствам ЭВМ = хороший то язык = Ассемблер
В настоящее время данный метод используется во всех системах автоматизированного приобретения
знаний. Репертуарная решетка с ее численными значениями может использоваться для исследования
понятий предметной области с учетом выявления временных конструктов.
Дерево решений – один из способов формализации и представления знаний
Эффективен там, где знания в виде правил. Деревья наглядно показывают ход (траектории) решения
задач. Причем траектории представляют собой эвристические знания эксперта о способе решения задач.
Более того, деревья в какой-то степени отражают субъективный личный опыт специалиста по решению
трудноформализуемых задач или опыт в принятии решений в управлении. Деревья в дальнейшем
позволяют легко конструировать продукционные правила, которые являются одной из основных форм
представления знаний.
Пример: ***
Построение нескольких деревьев помогает лучше структурировать знания. По деревьям решений можно
построить деревья фактов, которое является более формальным способом. В узлах дерева фактов стоят
утверждения или факты, представленные в виде пары “атрибут=значение”. Утверждения строятся из
вопроса и соответствующих ответов. Из вопроса конструируется атрибут, а его значением является
ответ на вопрос.
Пример: ***
С помощью дерева фактов строятся продукционные правила: рассматриваются все возможные пути от
корня к листьям. Для каждого пути записывается продукционное правило.
Пример: ***
К сожалению, не для всех предметных областей можно записать продукционные правила.
Метод извлечения знаний из БД
Метод генерирует продукционные правила. В методе используется представление знаний в виде
деревьев решений.
Рассмотрим пример:
Пусть необходимо построить базу знаний для получения ответа “как поступить, чтобы прибыль росла?”
Имеется некоторая БД – информация о продаже ПО и компьютеров:
Прибыль
Возраст
Конкуренция
Тип
падает
старый
нет
ПО
падает
средний
есть
ПО
растет
средний
нет
ЭВМ
падает
старый
нет
ЭВМ
растет
новый
нет
ЭВМ
растет
новый
нет
ПО
растет
средний
нет
ПО
растет
новый
есть
ПО
падает
средний
есть
ЭВМ
падает
старый
есть
ПО
Искомый атрибут “прибыль” будем называть атрибутом класса (атрибут цели). Для построения дерева
решений нужно взять один из атрибутов таблицы в качестве основного (корневого). Пусть это будет
“возраст”. Преобразуем исходную таблицу к виду:
Падает
Падает
Падает
Растет
Растет
Растет
Падает
Растет
Растет
Падает
Ст
Ст
Ст
Н
Н
Н
Ср
Ср
Ср
Ср
Н
Н
Е
Н
Н
Н
Е
Н
Н
Е
ПО
ЭВМ
ПО
ЭВМ
ПО
ПО
ПО
ЭВМ
ПО
ЭВМ
Т.о., произвели сортировку по колонке “возраст”
Далее проводится анализ полученной таблицы по графе “прибыль”. Из таблицы видно, что при
значении “Возраст”=“Старый” прибыль всегда падает, а при значении “Новый” – всегда растет. В
случае же значения “Средний” такого определенного вывода сделать нельзя. Поэтому продолжим
разбивку таблицы по атрибуту “конкуренция”. Получим другую таблицу. В результате расширяется
дерево решений.
растет
нет
растет
Возраст =
конкуренция
средний
падает
падает
да
Поскольку теперь для атрибута класса наше дерево решений выводит однозначный ответ, то дерево
решений построено.
Порождаем правила:
1. Если возраст=новый то прибыль=растет
2. Если возраст=старый то прибыль=падает
3. Если возраст=средний и конкуренция=нет то прибыль=растет
4. Если возраст=средний и конкуренция=есть то прибыль=падает
Не всегда можно построить дерево решений. Очередность рассмотрения атрибутов в таблице роли не
играет.Данный метод используется практически во всех системах автоматизированного приобретения
знаний.
Типовая структура экспертной системы
Экспертная система – это интеллектуальная система, предназначенная для решения задач в конкретной
предметной области.
Интерфейс
пользователя
Решатель
База знаний
Специалист в
предметной
области,
квалификация
которого
недостаточна
Подсистема
объяснений
Интеллектуальный
редактор
базы знаний
Инженер по
знаниям
+ Эксперт
Работу с системой ведут следующие специалисты:
– эксперт – высококвалифицированный специалист в предметной области;
– инженер по знаниям – посредник между экспертом и экспертной системой.
Компоненты экспертной системы имеют следующее назначение:
– решатель (машина дедуктивного вывода) – программа, осуществляющая вывод решений по
исходным вводимым ситуациям с использованием базы знаний, в литературе решатель
называют также “машиной логического вывода”, “интерпретатором правил”;
– база знаний – содержит знания эксперта о методах решения задач предметной области,
знания могут храниться в одной из следующих форм:
1) продукционные правила;
2) фреймы;
3) семантические сети;
– подсистема объяснений – объясняет процесс вывода результата, отвечает на вопросы “Как?”,
“Почему?”;
– редактор базы знаний – обеспечивает расширение базы знаний, позволяет добавлять новые
продукционные правила или другие элементы знаний.
Этапы разработки ЭС
Экспертная система как программный продукт разрабатывается по определенной технологии. Этапы
технологического цикла представлены на следующем рисунке.
1) Выбор проблемы
2) Разработка прототипа ЭС
3) Доработка до промышленной ЭС
4) Оценка ЭС
5) Стыковка ЭС
6) Поддержка ЭС
При выборе проблемы выполняются следующие действия:
1) определение цели разработки ЭС;
2) составление перечня решаемых задач;
3) нахождение экспертов;
4) оценка экономической целесообразности разработки.
В качестве прототипа разрабатывается усеченный вариант ЭС, на котором проверяется правильность
подходов, используемых при проектировании экспертной системы. Создание прототипа разбивается на
ряд этапов:
1) описание предметной области;
2) извлечение и приобретение знаний;
3) структурирование знаний;
4) формализация знаний;
5) выбор формы представления знаний (продукции, фреймы, сети);
6) запись знаний в этой форме;
7) программная реализация прототипа (включает от 10 до нескольких десятков правил).
Доработка до промышленной экспертной системы – это расширение базы знаний, ее пополнение
новыми знаниями, расширение функций интерфейса.
На этапе оценки проводится проверка работы экспертной системы другими экспертами.
Стыковка – это интеграция экспертной системы с другими программными системами.
Поддержка – сопровождение и модернизация экспертной системы.
Данная технология применяется для разработки систем, основанных на знаниях.
Общая схема:
Задача
(запрос,
ситуация)
Решение
СОЗ,
ЭС
Реализуется
непроцедурный
подход
БЗ
Инструментальные системы создания ЭС
В настоящее время существует много инструментальных систем создания ЭС, можно говорить от целой
индустрии интеллектуальных систем. Работа по созданию интеллектуальных систем ведется в двух
направлениях:
– создание прикладных экспертных систем;
– создание инструментальных средств.
Существует много оболочек для быстрого построения экспертных систем: GURU, Интер-Эксперт, UP –
Expert и др. Существующие оболочки целесообразно сравнивать по следующим параметрам:
– форма представления знаний;
– особенности работы механизма логического вывода (обратный или прямой вывод);
– возможности интерфейса;
– способность интегрироваться с другими программами;
– коммерческие характеристики;
– число типов ЭВМ, на которых функционирует оболочка.
Стратегии вывода можно представить следующим треугольником:
цель
обратный
вывод
прямой
вывод
исходные ситуации
(данные)
Изображенный треугольник содержит траектории, ведущие от исходных данных к цели (прямой вывод)
или от цели к исходным данным (обратный вывод).
Оболочки – это “пустые” системы, требующие наполнения базы знаний конкретными знаниями. Все
оболочки предоставляют возможность создания экспертных систем, работающих в режиме советчикаконсультанта.
Механизм логического вывода (интерпретатор правил)
Функции МЛВ:
1) просмотр существующих фактов в рабочей памяти (БД) и правил из БЗ, добавление в БД новых
фактов;
2) определение порядка просмотра и применения правил;
3) логический вывод новых заключений и фактов.
МЛВ реализуется небольшой программой. Механизм, как правило, встроен в оболочку экспертной
системы. Существуют 2 основных стратегии логического вывода:
– прямой порядок вывода;
– обратный порядок вывода.
В системах диагностики чаще применяется прямой вывод, в планирующих системах более
эффективным оказывается обратный вывод.
Обратный логический вывод
Вывод, при котором поиск доказательства начинается с целевого утверждения. Выясняются условия,
при которых целевое утверждение является выводимым. Эти условия принимаются за новые целевые
утверждения, и процесс поиска все очередные условия оказываются аксиомами или процесс обрывается
неудачей. Рассмотрим одну из моделей обратного логического вывода. В модели используются понятия
индексных карточек. Карточка представляет один какой-нибудь элемент БЗ:
– правило;
– атрибут и его значение.
Карточка атрибута содержит его имя и подсказку, если она есть.
Подсказка – это вопроса, который появляется на экране для получения от пользователя информации о
некотором атрибуте, значение которого неизвестно. С атрибутом может быть связан еще один
компонент – перевод: строка, раскрывающая значение атрибута, что улучшает восприятие.
Набор карточек образует базу данных экспертной системы.
Для работы МЛВ (дедуктивной машины) необходимы два стека.
Стек целей – хранит текущие цели. Это колода карточек атрибутов. В начале работы в стек кладем
карточку с конечной целью. В процессе работы этот стек накапливает последовательность всех
установленных фактов. В этот стек рядом с карточкой атрибута помещают карточку с его значением
(ответ пользователя). В алгоритме обратного вывода можно выделить следующие основные этапы:
1. Выбор продукционного правила для оценки
Делается попытка найти карточку в колоде правил, которая в своем заключении дает информацию об
атрибуте текущей цели (поэтому метод называется обратным выводом). Если такое правило,
содержащее в своем заключении атрибут текущей цели, найдено, то переходят к оценке правила. В
противном случае необходимо запросить у пользователя информацию.
2. Оценка правила
Проводится поочередное сопоставление утверждений из условной части правила с фактами базы
данных. Три возможных ситуации:
1) правило не поддается оценке (значение правила неизвестно) – один или несколько атрибутов в
условии отсутствуют в стеке контекстов. Карточка с неизвестным атрибутом помещается в стек
целей вместе с карточкой, содержащей неизвестное правило. Далее выбирается следующее правило
для оценки;
2) ложное правило – если одно из утверждений условия противоречит факту в стеке контекстов –
карточку текущего правила помещают в колоду сброса, возвращаются к этапу “выбор правила для
оценки”;
3) правило считается истинным – когда каждое утверждение условия согласуется с соответствующим
компонентом в стеке контекстов – подцель считается доказанной, текущая цель удаляется из
вершины стека целей и помещается затем в стек контекста. Карточка с правилом, извлеченным
ранее из стека целей, должна быть вновь помещена в вершину колоды правил и переоценена.
Опрос пользователя:
Если не найдено правило для текущей цели, то пользователь должен ее предоставить. Для этого служат
подсказки.
Функциональные возможности оболочки GURU
В настоящее время экспертные системы обычно используются для научных и медицинских
применений. С введением экспертных систем в сферу коммерции появилась возможность совместного
использования и усовершенствования специальных знаний людей. ЭВМ могут помочь при принятии
решений, при стратегическом планировании, при выборе решения вопроса о капиталовложениях, при
анализе риска и при прогнозировании. Они могут дать квалифицированный совет по любой проблеме,
связанной с управлением.
Новый подход к искусственному интеллекту позволил использовать электронные средства принятия
решений в сфере коммерции.
В результате применения нового подхода появился совершенно новый продукт ПО, названый GURU,
который был разработан специально для коммерции.
Система GURU расширяет возможности ИИ не только за счет того, что она может работать на
персональных ЭВМ, но также за счет меню и интерфейса на естественном языке. Управляющие могут
сами составлять наборы правил (при желании) и могут даже инициировать консультации с экспертной
системой и делать информационный запрос, используя обычный английский. Естественно-языковое
средство системы GURU снабжено большим словарем, оно легко запоминает новые слова, помнит
контекст диалогов и даже распознает типографские и орфографические ошибки.
Система GURU дает эффективные и широкие возможности искусственного интеллекта. Она решает как
простые, так и сложные проблемы, проблемы, которые требуют знаний экспертов и которые нельзя
решить с помощью обычной обработки данных.
Основой успеха системы GURU в мире коммерции является объединение экспертных систем и
известных вычислительных средств, предназначенных для решения коммерческих задач.
Знания, аргументация и эмпирические определения коммерческих экспертов могут храниться в
экспертной системе, базирующейся на GURU. Когда требуется совет эксперта, система обращается за
консультацией к этим знаниям и к вашей базе данных, работает даже в случае неточной информации,
проводит аргументацию в прямом или обратном направлении, и в случае необходимости требует
дополнительную информацию, дает рекомендации и даже объясняет ход доказательства. Система
GURU объединяет коммерческие данные и критерии принятия решений, отличаясь при этом
последовательностью и памятью, не дающей сбоев.
Экспертная система, разрабатываемая на основе GURU, может обращаться к имеющимся в наличии
данным, используя такие известные вычислительные средства, предназначенные для коммерции, как
реляционные базы данных, язык запросов, статистический анализ, электронные ведомости, управление
формами, графы, отчеты и дистанционную связь. Эти средства доступны во время процесса
аргументации. При обработке запроса на совет эксперта, система GURU может осуществлять
автоматический поиск информации и подсчет новых цифр, используя при этом администратора базы
данных, электронные ведомости и статистический анализ.
В случае необходимости, экспертная система может даже дать команду телекоммуникационному
средству ЭВМ найти удаленную базу данных. Заключения, сделанные экспертной системой GURU,
могут автоматически объединяться в хорошо документированных отчетах и графах.
С помощью администратора набора правил GURU можно составлять, хранить и модифицировать
правила, представляющие знания и объяснения экспертов. GURU предоставляет свободу в выражении
правил. В отличие от большинства экспертных систем GURU не устанавливает максимум на число
правил, которое может находиться в одном наборе.
Система GURU особенно сведуща в решении обычных административных вопросов... например, в том,
чтобы дать совет по выполнению текущих операций или сообщить инструкции по заполнению бланков,
формуляров. Она может способствовать более гибкой работе учреждения.
Широкие возможности GURU раскрываются не только в управлении, ее выгодно использовать на
любом уровне коммерции. В производстве GURU оказывает помощь в планировании, в упорядочении
компонентов и в распределении ресурсов для многочисленных средств. Можно разработать экспертные
системы для ремонта оборудования и поиска неисправностей. Параметры для принятия решений
служащими можно задать таким образом, что через вашу организацию будет осуществляться
корпоративная политика.
Несмотря на то, что GURU была разработана для удовлетворения нужд коммерции, ее специальные
знания можно использовать для научных, исследовательских и медицинских применений. С помощью
GURU можно успешно решить любую задачу, требующую объединения хранимой информации и
знаний экспертов. Систему GURU можно использовать для анализа результатов теста, для анализа
вариантов, для генерации отчетов. GURU – неоценимое средство поддержки решений.
Инструментальные средства GURU
Система GURU обрабатывает присвоенные посылкам и заключениям правил степени уверенности,
которые находятся в пределах диапазона 0 – 100. Степени уверенности можно также присвоить
значениям переменных и многочисленным значениям нечетких переменных. Система GURU
предоставляет возможность выбрать нужный вариант из 16 отдельных вариантов алгебры,
используемой для объединения степеней достоверности переменных и правил.
GURU написана на языках С и ассемблер и работает достаточно быстро, а также имеет высокую
степень интеграции с вычислительными средствами, предназначенными для коммерции.
Система GURU включает в себя администратор реляционной базы данных, язык запросов, электронные
ведомости, генератор статистических данных, средства управленческой графики, генератор отчетов и
средства телекоммуникации. Все эти средства объединены, поэтому при разработке наборов правил и
при консультациях вы можете обращаться к информации с помощью этих источников.
Приводимые ниже характеристики помогут при разработке экспертных систем:
– Ввод данных пользователя и выбор вариантов: можно составить такие правила, которые будут
обращаться к пользователю экспертной системы с помощью построчных подсказок, форм и
меню. Все эти средства очень удобны для пользователя.
– Многочисленные и недостоверные ответы: на каждый вопрос можно дать несколько
потенциально правильных ответов (для хранения в нечеткой переменной) и указать уровни
достоверности (0 - 100) для каждого возможного ответа. Система GURU работает с
недостоверной информацией и использует степень достоверности, указанную с целью
обеспечения достоверности ответа.
– Написание правил: можно писать правила, используя непосредственные команды, текстовой
процессор и составитель набора правил, управляемый меню.
– Объяснение типа “как” и “почему”: при написании правил в раздел объяснений можно включить
столько слов, сколько требуется. Эта информация потом воспроизводится на экране в тех
случаях, когда пользователю необходимо знать, почему GURU требует достоверной
информации, или каким путем она пришла к той или иной рекомендации. Эти объяснения
оказывают вам значительную помощь, при настройке экспертной системы.
– Прослеживание логических выводов: можно потребовать, чтобы во время конкретной
консультации была представлена полная последовательность доказательств по мере его
развития. Это позволит обнаружить неожиданные моменты в процессе аргументации при
разработке набора правил.
– Редактирование базы знаний в режиме он-лайн: наборы правил можно редактировать, используя
либо администратор правил, управляемый меню, либо интегрированный текстовой процессор.
– Определение местоположения конкретных атрибутов: если переменная изменилась, ее можно
найти и модифицировать, используя текстовой процессор для изменения всех обращений к этой
переменной.
– Утилиты форматов экрана: с помощью гибких команд ввода/вывода, интегрированного языка
программирования и администратора форм вы можете получить или представить информацию в
любом требуемом формате.
– Доступ к операционной системе: для доступа к операционной системе с целью выполнения
внешних программ или использования команд DOS можно применять команду RUN системы
GURU.
Методика проектирования экспертных систем в GURU
Инструментальная среда GURU является продукционной средой построения экспертных систем,
поэтому проектирование ЭС в этой среде заключается в написании правил. Продукционное правило
состоит из нескольких частей.
Первая часть правила – посылка
В зависимости от требований посылка правила GURU может быть предельно простой и предельно
расширенной и может включать в себя много элементов:
– рабочие переменные с одним значением;
– многозначные нечеткие переменные для представления недостоверных знаний;
– статистические переменные;
– ячейки электронных ведомостей;
– поля базы данных;
– элементы массива (одномерные и двумерные);
– операторы отношений (EQ, NE, GT, GE, LE, IN);
– булевы операторы AND, OR, XOR, NOT;
– операторы над числами (+, -, /, *, **);
– числовые функции (SIN, COSIN, LOG, SQRT и т.д.);
– различные операции над текстовыми строками;
– символы, соответствия классу символов и символам поиска по неполной информации.
Вторя часть правила – заключение.
Заключение правила системы GURU может состоять из целого ряда команд. Примеры содержат
следующие операции:
– присвоение новых знаний переменным, массивам, полям и т.д;
– хранение записей в базе данных;
– обращение за консультацией к другому набору правил;
– присвоение новых определений ячейкам электронной ведомости;
– автоматический перерасчет всей электронной ведомости или ее части;
– выполнение программы GURU, которая содержит такие структуры управления, как if-then-else,
test-case, while-do;
– взаимодействие с пользователем посредством многоцветных форм, соответствующих
требованиям заказчика;
– генерация любых управленческих графических данных на основе переменной, массива или на
основе данных электронной ведомости;
– проведение выборочного статистического анализа на основе содержимого таблиц базы данных;
– генерация отчетов, отвечающих требованиям пользователя и организованных согласно
тщательно разработанным шаблонам;
– выполнение операции пересылки символа, строки, пакета или файла с помощью удаленной
ЭВМ.
Независимо от того, используется ли при проектировании экспертной системы команды с прямой
адресацией, меню или текстовой процессор, при разработке ЭС всегда можно получить оперативную
помощь в соответствии с условиями контекста.
Программирование раздела инициализации INITIAL
Предложение инициализации содержит операторы, которые GURU выполняет тогда, когда начинается
консультация с экспертной системой.
Операторы могут относиться к любому типу операторов GURU. Обычно, вы вводите значения
переменных среды и получаете значения переменных, которые не используются в правилах.
Предложение инициализации начинается с INITIAL. После этого следуют операторы.
Пример:
INITIAL: E.STAT=FALSE
SALES=UNKNОWN
INPUT SALESMAN WITH "Введите имя продавца"
В этот момент можно задать любые начальные условия, которые необходимы пользователю для
консультации с экспертной системой. Если предложения инициализации превышают несколько строк,
операторы можно поместить в выполнимый файл и затем использовать оператор PERFORM в
предложении инициализации. Таким образом, вы можете изменить последовательность операторов
инициализации, редактируя файл выполнения, при этом устраняется необходимость в повторной
компиляции набора правил.
Программирование раздела описания переменных VAR
Предложения переменных описывают переменные, которые использует экспертная система. Если
переменная применяется либо в посылке, либо в заключении правила, она должна быть определена.
Предложение переменной начинается с VARIABLE. После этого идет имя переменной, за которым
следует ряд предложений, самыми важными из которых являются FIND и LABEL.
Пример:
VARIABLE: SALES
SALES – имя переменной, которую используют одно или несколько правил в наборе.
Предложение LABEL:
Предложение LABEL содержит краткое (менее 64 символов) описание переменной. Метка – это
то, что видит пользователь, когда команды HOW или WHY показывают переменные, используемые
конкретным правилом. Меткой должно быть описание переменной.
Пример:
LABEL: Общий объем продаж за этот год.
Предложение FIND:
Предложение FIND содержит один или несколько операторов GURU, которые следует
использовать тогда, когда необходим ввод значения переменной. Обычно, это какая-нибудь форма
оператора INPUT или GETFORM, хотя здесь разрешаются все операторы GURU.
Пример:
FIND: INPUT SALES WITH “Введите общий объем продаж за этот год”
Если системе GURU необходимо знать значение неизвестной переменной, она прежде всего
пытается найти правило, которое дает значение переменной. Если система не находит правило, она
выполняет операторы в FIND для того, чтобы выяснить значение у пользователя.
Преимущества использования оператора PROMPT:
– Пользователь запрашивается только в том случае, когда требуется значение.
– Если пользователю необходимо знать, почему появилась подсказка, нажатием клавиши он
сможет получить объяснения относительно того правила, которое оценивается в этот момент.
Если значение вводится во время инициализации, в сообщении, которое видит пользователь на
экране, содержится значительно меньше информации.
Программирование раздела описания правил RULE
Набор правил должен включать в себя, по крайней мере, одно правило.
Каждое правило начинается с RULE, за которым следует имя правила и еще ряд предложений.
Пример:
RULE: RPROFIT,
где RPROFIT – имя правила.
Наиболее важными предложениями являются предложения IF, THEN и REASON.
IF: предложение
В предложении IF содержится посылка правила. Оно начинается с IF, за которым следует
выражение, которое может быть истинным, ложным или неизвестным.
Пример:
IF: SALES> EXPENSES
Если сбыт (SALES) выше, чем затраты (EXPENSES), тогда посылка истинна. Если SALES ниже,
чем EXPENSES, посылка ложна.
Если SALES или EXPENSES не известны, посылка считается неизвестной.
Предложение THEN:
В предложении THEN содержится заключение правила. Оно начинается с THEN. После THEN
может идти любое количество операторов GURU.
Пример:
THEN: PROFIT = SALES – EXPENSES
Если посылка в предложении IF истина, GURU выполняет операторы в заключении. Это
известно как запуск правила.
Если посылка ложна, операторы в заключении не выполняются, и правило не запускается.
Если посылка не известна, GURU пытается определить значение ее переменных. Обычно, GURU
ищет другое правило, которое дает значения переменных в посылке или запрашивает значения. Как
только все переменные становятся известными, система GURU повторно оценивает посылку. Если
посылка истинна, правило выполняется.
Если нет, правило не запускается.
Предложения IF и THEN необходимы. Они должны присутствовать в каждом правиле.
Предложение объяснения (REASON)
В предложении REASON содержится объяснение правила. Оно начинается с REASON. После
REASON может идти любой текст.
Программирование раздела завершения DO
Предложение завершения содержит операторы GURU, которые выполняются после того, как значение
переменной цели найдено и консультация закончена. Распечатайте значение переменной цели и
выполните работу по освобождению ресурсов для завершения. Предложение завершения начинается с
DO, за которым может следовать любое количество операторов GURU.
Пример:
DO: OUTPUT “Ответ:”, MYGOAL
Анализ результатов принятия решений с помощью разработанной ЭС
После обращения к набору правил с целью консультации пользователь может попросить систему
объяснить, какие правила и переменные использовались. Для этого используются две команды: HOW –
выдает переменные, которые использовались. WHY – объясняет правила, которые использовались.
HOW – выдает значение или значения переменной цели, правило или правила, с помощью
которых была определена цель, а также сообщает результирующие факторы уверенности.
WHY – воспроизводит на экране дисплея объяснения (REASON) и переменные, которые
требовались для правила, выполняющегося последним.
REASON появляется, когда пользователь экспертной системы выдает команду WHY или
нажимает клавишу WHY (^Y). Так как при появлении REASON пользователь не видит самого правила,
лучше всего начать предложение REASON с изложения правила и затем добавить любую
дополнительную информацию, которая нужна пользователю. Длина предложения REASON
определяется требованиями пользователя.
Пример:
REASON: Если доход от сбыта превышает расходы, тогда прибыль равняется доходам от
сбыта минус расходы.
Присутствие предложения REASON не обязательно, но очень рекомендуется. Без этого предложения
пользователи экспертной системы не смогут изучить ход процесса аргументации.