Итоговая тестовая работа по математике за 1 четверть, 11 класс

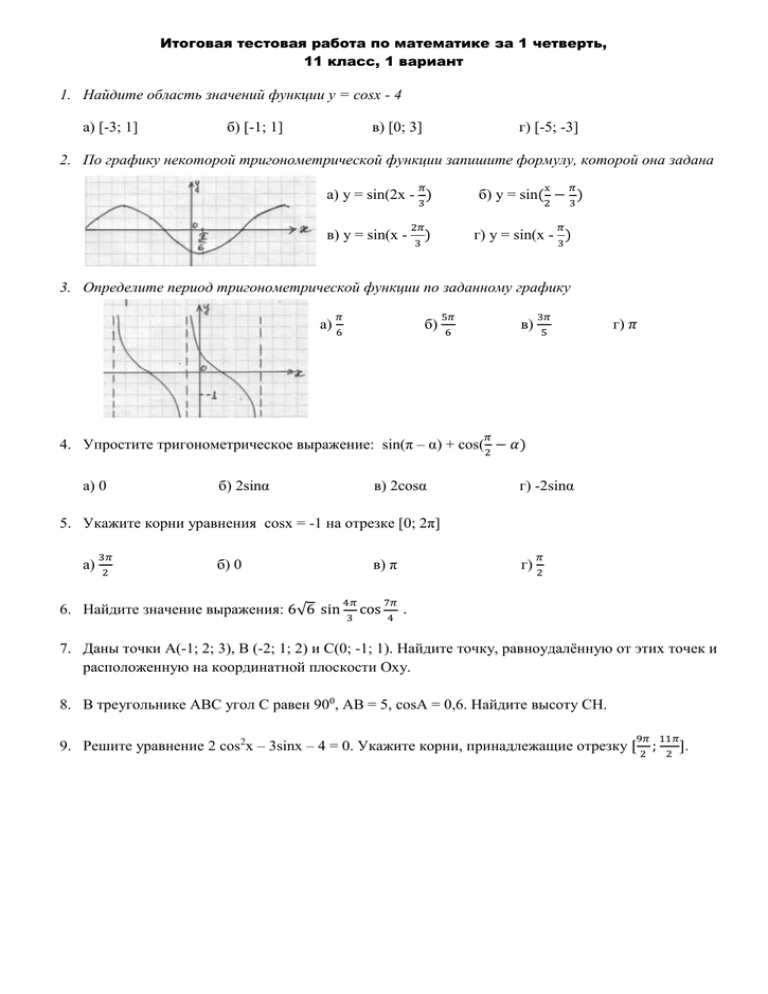
Итоговая тестовая работа по математике за 1 четверть,
11 класс, 1 вариант
1. Найдите область значений функции у = cosx - 4
а) [-3; 1]
б) [-1; 1]
в) [0; 3]
г) [-5; -3]
2. По графику некоторой тригонометрической функции запишите формулу, которой она задана
𝜋
х
а) у = sin(2x - 3 )
в) у = sin(х -
𝜋
б) у = sin(2 − 3 )
2𝜋
𝜋
г) у = sin(х - 3 )
)
3
3. Определите период тригонометрической функции по заданному графику
𝜋
а) 6
б)
5𝜋
в)
6
3𝜋
5
г) 𝜋
𝜋
4. Упростите тригонометрическое выражение: sin(π – α) + cos( 2 − 𝛼)
а) 0
б) 2sinα
в) 2cosα
г) -2sinα
5. Укажите корни уравнения cosх = -1 на отрезке [0; 2π]
а)
3𝜋
2
б) 0
6. Найдите значение выражения: 6√6 sin
𝜋
в) π
4𝜋
3
cos
7𝜋
4
г) 2
.
7. Даны точки А(-1; 2; 3), В (-2; 1; 2) и С(0; -1; 1). Найдите точку, равноудалённую от этих точек и
расположенную на координатной плоскости Оху.
8. В треугольнике АВС угол С равен 900, АВ = 5, cosA = 0,6. Найдите высоту СH.
9𝜋 11𝜋
9. Решите уравнение 2 cos2x – 3sinx – 4 = 0. Укажите корни, принадлежащие отрезку [ 2 ;
2
].
Итоговая тестовая работа по математике за 1 четверть,
11класс, 2 вариант
1. Найдите область значений функции у = sinx + 2
а) [-1; 1]
б) [1; 3]
в) [0; 2]
г) [2; 3]
2. По графику некоторой тригонометрической функции запишите формулу, которой она задана
𝜋
б) у = cos(2 − 3 )
х
2𝜋
г) у = cos(х + 3 )
а) у = cos(2x - 3 )
в) у = cos(х +
𝜋
𝜋
)
3
3. Определите период тригонометрической функции по заданному графику
а)
3𝜋
б)
4
2𝜋
𝜋
5𝜋
в) 2
3
6
1. Упростите тригонометрическое выражение: cos(π + α) +
3𝜋
sin( 2 − 𝛼)
а) 0
б) -2cosα
в) 2cosα
г) -2sinα
3𝜋
4. Упростите тригонометрическое выражение: cos(π + α) + sin( 2 − 𝛼)
а) 0
б) -2cosα
в) 2cosα
г) -2sinα
5. Укажите корни уравнения sinх = -1 на отрезке [0; 2π]
а)
3𝜋
2
б) 0
6. Найдите значение выражения:
в) π
𝜋
г) 2
ctgα∙cos(π−α)
cos α
, если tgα = 5.
7. Даны точки А(-1; 2; 3), В (-2; 1; 2) и С(0; -1; 1). Найдите точку, равноудалённую от этих точек и
расположенную на координатной плоскости Охz.
1
8. В равнобедренном треугольнике АВС с основанием АС = 3√2, cos С = 3. Найдите высоту СК.
9. Решите уравнение: 2sinx – cosx – 1 =0. Укажите корни, принадлежащие отрезку [3𝜋; 4𝜋]