Муниципальный этап Всероссийской олимпиады школьников по физике

Муниципальный этап
Всероссийской олимпиады школьников по физике
11 класс (2014 – 2015 учебный год)
Решение заданий оформляются в тетради. Не забудьте поставить на титульном листе тетради ваш идентификационный код и класс!
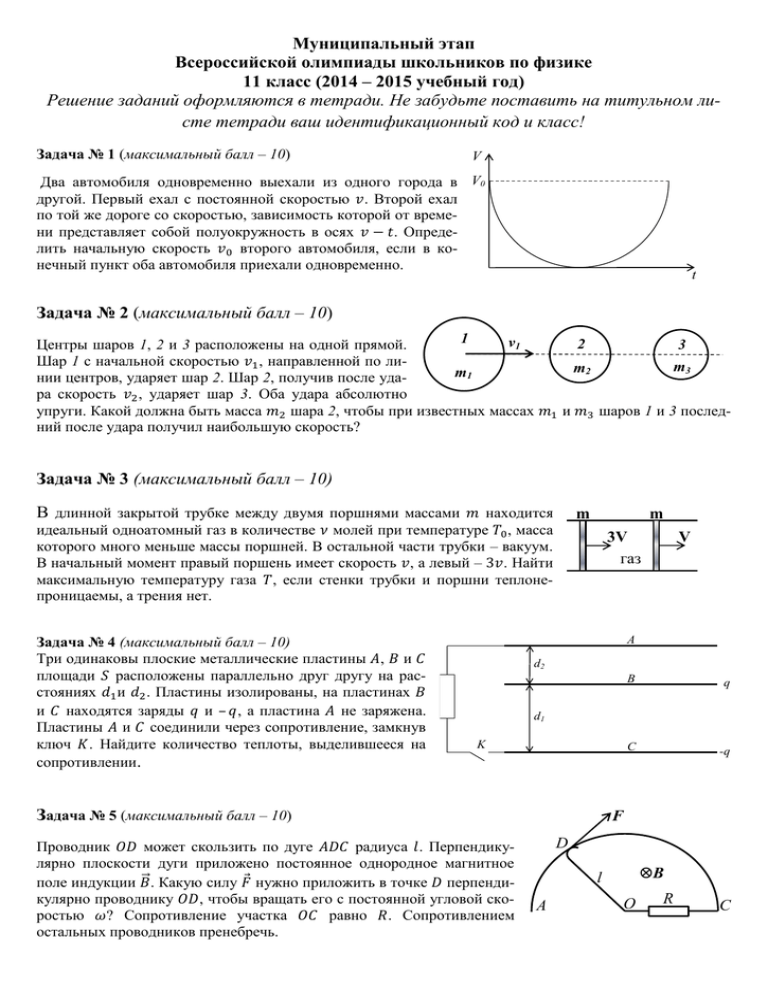
Задача № 1 (максимальный балл – 10)
V
Два автомобиля одновременно выехали из одного города в V0
другой. Первый ехал с постоянной скоростью 𝑣. Второй ехал
по той же дороге со скоростью, зависимость которой от времени представляет собой полуокружность в осях 𝑣 − 𝑡. Определить начальную скорость 𝑣0 второго автомобиля, если в конечный пункт оба автомобиля приехали одновременно.
t
Задача № 2 (максимальный балл – 10)
1
v1
2
Центры шаров 1, 2 и 3 расположены на одной прямой.
3
Шар 1 с начальной скоростью 𝑣1 , направленной по лиm3
m2
m1
нии центров, ударяет шар 2. Шар 2, получив после удара скорость 𝑣2 , ударяет шар 3. Оба удара абсолютно
упруги. Какой должна быть масса 𝑚2 шара 2, чтобы при известных массах 𝑚1 и 𝑚3 шаров 1 и 3 последний после удара получил наибольшую скорость?
Задача № 3 (максимальный балл – 10)
В длинной закрытой трубке между двумя поршнями массами 𝑚 находится
идеальный одноатомный газ в количестве 𝜈 молей при температуре 𝑇0 , масса
которого много меньше массы поршней. В остальной части трубки – вакуум.
В начальный момент правый поршень имеет скорость 𝑣, а левый – 3𝑣. Найти
максимальную температуру газа 𝑇, если стенки трубки и поршни теплонепроницаемы, а трения нет.
Задача № 4 (максимальный балл – 10)
Три одинаковы плоские металлические пластины 𝐴, 𝐵 и 𝐶
площади 𝑆 расположены параллельно друг другу на расстояниях 𝑑1 и 𝑑2 . Пластины изолированы, на пластинах 𝐵
и 𝐶 находятся заряды 𝑞 и – 𝑞, а пластина 𝐴 не заряжена.
Пластины 𝐴 и 𝐶 соединили через сопротивление, замкнув
ключ 𝐾. Найдите количество теплоты, выделившееся на
сопротивлении.
m
m
3V
газ
V
A
d2
B
q
C
-q
d1
K
Задача № 5 (максимальный балл – 10)
Проводник 𝑂𝐷 может скользить по дуге 𝐴𝐷𝐶 радиуса 𝑙. Перпендикулярно плоскости дуги приложено постоянное однородное магнитное
⃗ . Какую силу 𝐹 нужно приложить в точке 𝐷 перпендиполе индукции 𝐵
кулярно проводнику 𝑂𝐷, чтобы вращать его с постоянной угловой скоростью 𝜔? Сопротивление участка 𝑂𝐶 равно 𝑅. Сопротивлением
остальных проводников пренебречь.
F
D
B
l
A
O
R
C
РЕШЕНИЯ
Задача 1. Два автомобиля одновременно выехали из V
одного города в другой. Первый ехал с постоянной V0
скоростью 𝑣. Второй ехал по той же дороге со скоростью, зависимость которой от времени представляет
собой полуокружность в осях 𝑣 − 𝑡. Определить
t
начальную скорость 𝑣0 второго автомобиля, если в
конечный пункт оба автомобиля приехали одновременно.
Решение:
1. Путь 𝑆, пройденный первым автомобилем за время 𝑡cпостоянной скоростью 𝑣, определяется соотношением 𝑆 = 𝑣 ∙ 𝑡.
2. Такой же путь 𝑆, пройденный вторым автомобилем за то же время 𝑡, определяется
площадью под графиком скорости в осях 𝑣 − 𝑡.
3. Заметим, что площадь под графиком скорости в осях 𝑣 − 𝑡 равна разности между площадью прямоугольника со сторонами 𝑣0 и 𝑡 и половины круга с радиусом 𝑣0 или 𝑡⁄2:
𝜋
𝑡
4−𝜋
2
2
4
𝑆 = 𝑣0 ∙ 𝑡 − ∙ 𝑣0 ∙ = 𝑣0 ∙ 𝑡 ∙
.
4. Из условия равенства путей получаем выражение для определения начальной скорости
второго автомобиля 𝑣0 :
𝑣 ∙ 𝑡 = 𝑣0 ∙ 𝑡 ∙
4−𝜋
4
.
5. Разрешая последнее равенство относительно 𝑣0 , получаем ответ:
𝑣0 =
Ответ:𝑣0 =
4
4−𝜋
4
4−𝜋
∙ 𝑣.
∙ 𝑣.
Количество
баллов
1
2
4
2
1
Критерии оценки
Записана формула пути, пройденного первым автомобилем (пункт 1)
Указано, что путь равен площади под графиком скорости (пункт 2)
Определена площадь под графиком скорости (пункт 3)
Записано условие равенства пройденных путей (пункт 4)
Получен окончательный ответ (пункт 5)
Задача 2.Центры шаров 1, 2 и 3 расположены
на одной прямой. Шар 1 с начальной скоро-
1
стью 𝑣1 , направленной по линии центров,
m1
ударяет шар 2. Шар 2, получив после удара
v1
2
3
m2
m3
скорость 𝑣2 , ударяет шар 3. Оба удара абсолютно упруги. Какой должна быть масса
𝑚2 шара 2, чтобы при известных массах 𝑚1 и 𝑚3 шаров 1 и 3последний после удара получил наибольшую скорость?
Решение:
1. При центральных упругих ударах шары будут двигаться вправо вдоль одной прямой,
причём будут сохранятьсяимпульс и кинетическая энергия системы шаров.
2. Скорость 𝑣2 шара 2 после его соударения с шаром 1 определим, записав для шаров 1 и
2 законы сохранения импульса и энергии:
𝑚1 ∙ 𝑣1 = 𝑚1 ∙ 𝑢1 + 𝑚2 ∙ 𝑣2
{ 𝑚1∙𝑣12 𝑚1∙𝑢12 𝑚2∙𝑣22 ,
=
+
2
2
2
где 𝑢1 – скорость шара 1 после соударения с шаром 2.
3. Решая уравнения пункта 2, определим выражение для скорости 𝑣2 шара 2 после его
соударения с шаром 1:
2∙𝑚1
𝑣2 =
𝑚1 +𝑚2
∙ 𝑣1 .
4. По аналогии с ситуацией ударов шаров 1 и 2, для скорости шара 3 после его соударения с шаром 2 можно записать выражение:
2∙𝑚2
𝑣3 =
𝑚2 +𝑚3
∙ 𝑣2 .
5. Тогда, с учётом выражения для скорости шара 2, уравнение, определяющее скорость
шара 3 примет вид:
𝑣3 = (𝑚
4∙𝑚1 ∙𝑚2
1 +𝑚2 )∙(𝑚2 +𝑚3 )
∙ 𝑣1 .
6. Чтобы скорость шара 3 могла быть максимальной, необходимо потребовать равенства
нулю производной функции 𝑣3 = 𝑣3 (𝑚2 ):
𝑣3′ = [(𝑚
4∙𝑚1 ∙𝑣1
2
1 +𝑚2 )∙(𝑚2 +𝑚3 )]
∙ (𝑚1 ∙ 𝑚3 − 𝑚22 ) = 0.
7. Решая последнее уравнение относительно массы 𝑚2 шара 2, получим выражение:
𝑚2 = √𝑚1 ∙ 𝑚3 .
8. Покажем, что при значении массы 𝑚2 , определяемом последним выражением, функция 𝑣3 = 𝑣3 (𝑚2 ) достигает максимума. Действительно, график производной 𝑣3′ представляет собой параболу, ветви которой направлены вниз. Значение 𝑚2 , определённое в
пункте 7, является правой точкой пересечения графика производной 𝑣3′ с осью 𝑚2 , а зна-
чит, при переходе через неё производная 𝑣3′ меняет свой знак с плюса на минус, что
определяет значение 𝑚2 = √𝑚1 ∙ 𝑚3 как точку максимума функции 𝑣3 = 𝑣3 (𝑚2 ).
Ответ:𝑚2 = √𝑚1 ∙ 𝑚3 .
Количество
баллов
Критерии оценки
Описано движение шарови записаны законы сохранения кинетической
энергии и импульса(пункты 1,2)
Определена скорость шара 2 (пункт 3)
Записано выражение для скорости шара 3 (пункт 4)
Записано выражение для скорости шара 3 через скорость шара 1 (пункт 5)
Записано необходимое условие экстремума функции 𝑣3 (пункт 6)
Определена искомая масса (пункт 7)
Доказано, что найденное значение соответствует максимуму функции 𝑣3 =
𝑣3 (𝑚2 ) (пункт 8)
Задача 3. В длинной закрытой трубке между двумя поршнями масса- m
ми 𝑚 находится идеальный одноатомный газ в количестве 𝜈 молей при
температуре 𝑇0 , масса которого много меньше массы поршней. В
1
2
1
1
3
1
1
m
3V
газ
V
остальной части трубки – вакуум. В начальный момент правый поршень имеет скорость
𝑣, а левый – 3𝑣. Найти максимальную температуру газа 𝑇, если стенки трубки и поршни
теплонепроницаемы, а трения нет.
Решение:
1. Определим модуль скорости, с которой движется центр масс рассматриваемой системы. В связи с тем, что масса газа между поршнями много меньше массы поршней, то модуль скорости центра масс всей системы равен модулю скорости центра масс поршней и
определяется соотношением:
𝑣𝑐 =
𝑚∙𝑣+3∙𝑚∙𝑣
𝑚+𝑚
= 2 ∙ 𝑣.
2. Центр масс системы поршней движется в сторону движения поршней, поэтому относительно инерциальной системы отсчёта, движущейся со скоростью центра масс поршней 𝑣𝑐 , модули скоростей левого и правого поршня равны:
𝑣л = 3 ∙ 𝑣 − 2 ∙ 𝑣 = 𝑣, 𝑣п = 2 ∙ 𝑣 − 𝑣 = 𝑣.
3. Температура газа между поршнями станет максимальной в тот момент, когда кинетическая энергия поршней в системе отсчёта их центра масс станет равной нулю.
4. Для определения максимальной температуры газа𝑇 запишем закон сохранения энергии
в системе центра масс поршней:
𝑚∙𝑣л2
2
+
𝑚∙𝑣п2
2
3
𝑚∙𝑣 2
2
2
+ ∙ 𝜈 ∙ 𝑅 ∙ 𝑇0 =
+
𝑚∙𝑣 2
2
3
3
2
2
+ ∙ 𝜈 ∙ 𝑅 ∙ 𝑇0 = ∙ 𝜈 ∙ 𝑅 ∙ 𝑇.
5. Разрешив последнее уравнение относительно 𝑇, получаем ответ:
𝑇 = 𝑇0 +
Ответ:𝑇 = 𝑇0 +
2∙𝑚∙𝑣 2
3∙𝜈∙𝑅
2∙𝑚∙𝑣 2
3∙𝜈∙𝑅
.
.
Количество
баллов
3
2
2
2
1
Критерии оценки
Определена скорость центра масс поршней (пункт 1)
Определены скорости поршнейв системе центра масс (пункт 2)
Сформулировано условие максимальности температуры (пункт 3)
Записан закон сохранения энергии (пункт 4)
Получен окончательный ответ (пункт 5)
Задача 4. Три одинаковы плоские металлические пластины 𝐴, 𝐵и 𝐶площади
A
d2
𝑆расположены параллельно друг другу
B
q
C
-q
на расстояниях 𝑑1 и 𝑑2 . Пластины изоd1
лированы, на пластинах 𝐵 и 𝐶 находятся
K
заряды 𝑞 и – 𝑞, а пластина 𝐴 не заряже-
на. Пластины 𝐴 и 𝐶 соединили через сопротивление, замкнув ключ 𝐾. Найдите количество теплоты, выделившееся на сопротивлении.
Решение:
1. После замыкания ключа 𝐾 получим
A
эквивалентную схему с двумя последо-
-q2
C2 d2
вательно соединёнными конденсатора-
B
q2
q1
C
-q1
ми:
2. Энергия, запасённая в системе, до
C1 d1
замыкания ключа 𝐾 была равна энергии электрического поля конденсатора
ёмкостью 𝐶1 , образованного пластинами 𝐵 и 𝐶:
𝑊1 =
𝑞2
2∙𝐶1
.
3. Энергия электрического поля конденсаторов с ёмкостями 𝐶1 и 𝐶2 после замыкания
ключа 𝐾 равна:
𝑊2 =
𝑞12
2∙𝐶1
+
𝑞22
2∙𝐶2
.
4. Ёмкости 𝐶1 и 𝐶2 плоских конденсаторов определяются равенствами𝐶1 =
𝜀0 ∙𝑆
𝑑1
, 𝐶2 =
𝜀0 ∙𝑆
𝑑2
,
откуда следует соотношение:
𝐶2
𝐶1
=
𝑑1
𝑑2
.
5. Для рассматриваемой системы проводников выполняется закон сохранения электрического заряда, поэтому можно записать:
𝑞 = 𝑞1 + 𝑞2 .
6. В связи с тем, что пластины 𝐴 и 𝐶 соединены проводником, их потенциалы равны, а
значит равны и разности потенциалов между пластинами 𝐴 и 𝐵и пластинами 𝐵 и 𝐶, из
чего следует соотношение:
𝑞1
𝐶1
=
𝑞2
𝐶2
.
7. Решая совместно уравнения из пунктов 4 – 6, получим выражения для зарядов конденсаторов, образовавшихся на их обкладках после замыкания ключа 𝐾:
𝑞1 =
𝑞
1+𝑑1 ⁄𝑑2
, 𝑞2 =
𝑞
1+𝑑2 ⁄𝑑1
.
8. Из закона сохранения энергии следует, что количество теплоты, выделившееся на резисторе после замыкания ключа 𝐾, равно разности между значениями энергии электрического поля конденсаторов до и после замыкания ключа 𝐾:
𝑄 = 𝑊1 − 𝑊2 =
𝑞2
2∙𝐶1
−
𝑞12
2∙𝐶1
−
𝑞22
2∙𝐶2
.
9. Подставив в последнее уравнение значения зарядов 𝑞1 и 𝑞2 из пункта 7, а также ёмкостей 𝐶1 и 𝐶2 и пункта 4, получим искомое значение выделившейся на резисторе после
замыкания ключа 𝐾 энергии:
𝑄=
Ответ:𝑄 =
𝑞 2 ∙𝑑12
2∙𝜀0 ∙𝑆∙(𝑑1 +𝑑2 )
𝑞 2 ∙𝑑12
2∙𝜀0 ∙𝑆∙(𝑑1 +𝑑2 )
.
.
Критерии оценки
Изображена эквивалентная схема (пункт 1)
Записано выражение для энергии системы до замыкания ключа (пункт 2)
Записано выражение для энергии после замыкания ключа (пункт 3)
Записаносоотношение ёмкостей конденсаторов (пункт 4)
Записан закон сохранения заряда (пункт 5)
Записано условие равенства напряжений между пластинами (пункт 6)
Определены заряды конденсаторов (пункт 7)
Записан закон сохранения энергии (пункт 8)
Количество
баллов
1
1
1
1
1
1
1
2
Получен окончательный ответ (пункт 9)
Задача 5. Проводник 𝑂𝐷 может скользить по дуге 𝐴𝐷𝐶 ради-
1
F
уса 𝑙. Перпендикулярно плоскости дуги приложено постоян-
D
⃗ . Какую силу
ное однородное магнитное поле индукции 𝐵
𝐹 нужно приложить в точке 𝐷 перпендикулярно проводнику
B
l
A
O
R
C
𝑂𝐷, чтобы вращать его с постоянной угловой скоростью 𝜔? Сопротивление участка
𝑂𝐶 равно 𝑅. Сопротивлением остальных проводников пренебречь.
Решение:
1. При движении проводника 𝑂𝐷 под действием силы 𝐹 будет изменяться площадь
контура 𝑂𝐷𝐶, а значит будет изменяться магнитный поток Φ = B ∙ S, пронизывающий
этот контур.
2. По закону электромагнитной индукции Фарадея, при изменении магнитного потока
сквозь
замкнутый
проводящий
контур
в
нём
возникнет
ЭДС
индукции,
пропорциональная скорости изменения площади контура, модуль которой определяется
выражением:
𝜀𝑖 =
∆Φ
∆𝑡
∆S
=𝐵∙
∆𝑡
.
3. Замкнутый контур представляет собой круговой сектор, ограниченный радиусами 𝑂𝐷
и 𝑂𝐶длины 𝑙, площадь которого определяется выражением:
𝑆=
𝜑∙𝑙 2
2
,
где 𝜑 – угол между радиусами 𝑂𝐷 и 𝑂𝐶.
4. Тогда модуль ЭДС индукции, возникающей в замкнутом контуре 𝑂𝐷𝐶, будет равен:
𝜀𝑖 =
где
∆φ
∆𝑡
∆Φ
∆𝑡
=𝐵∙
∆S
∆𝑡
=
𝐵∙𝑙 2
2
∙
∆φ
∆𝑡
=
𝐵∙𝑙 2 ∙𝜔
2
,
= 𝜔 – искомая угловая скорость по определению.
5. Вследствие возникновения в замкнутом контуре 𝑂𝐷𝐶 ЭДС индукции, по нему потечёт
индукционный ток, величина которого определяется законом Ома:
𝐼=
𝜀𝑖
𝑅
=
𝐵∙𝑙 2 ∙𝜔
2∙𝑅
.
6. Для выполнения условия постоянства угловой скорости проводника 𝜔 необходимо,
чтобы работа силы 𝐹 по перемещению точки 𝑂 проводника 𝑂𝐷за любой малый промежуток времени 𝑡 полностью преобразовывалась в джоулево тепло, выделяемое на сопротивлении 𝑅при протекании индукционного тока 𝐼:
𝐹 ∙ 𝑟 = 𝐼 2 ∙ 𝑅 ∙ 𝑡,
где 𝑟 – модуль малого перемещения, совершённого концом 𝑂 проводника 𝑂𝐷 за малый
промежуток времени 𝑡.
7. Разделив последнее уравнение на малый промежуток времени 𝑡, получим равенство
мощностей силы 𝐹 и индукционного тока 𝐼, выделяемой на сопротивлении 𝑅:
𝐹 ∙ 𝑣 = 𝐼 2 ∙ 𝑅,
где 𝑣 = 𝜔 ∙ 𝑙 – линейная скорость конца 𝑂 проводника 𝑂𝐷.
8. Решая совместно уравнения из пунктов 5 и 7, определяем искомое выражение для модуля силы 𝐹 :
𝐹=
Ответ:𝐹 =
𝐵2 ∙𝑙 3 ∙𝜔
4∙𝑅
𝐵2 ∙𝑙 3 ∙𝜔
4∙𝑅
.
.
Критерии оценки
Указано на изменение магнитного потока сквозь контур (пункт 1)
Записано выражение для возникающей ЭДС индукции (пункт 2)
Записано выражение для площади контура (пункт 3)
Определена ЭДС индукции в контуре (пункт 4)
Рассчитан индукционный ток (пункт 5)
Записано условие постоянства угловой скорости (пункты 6,7)
Получен окончательный ответ (пункт 8)
Количество
баллов
1
1
1
2
1
3
1