решение 10.2 - Гимназия №1 имени К.Калиновского г.Свислочь

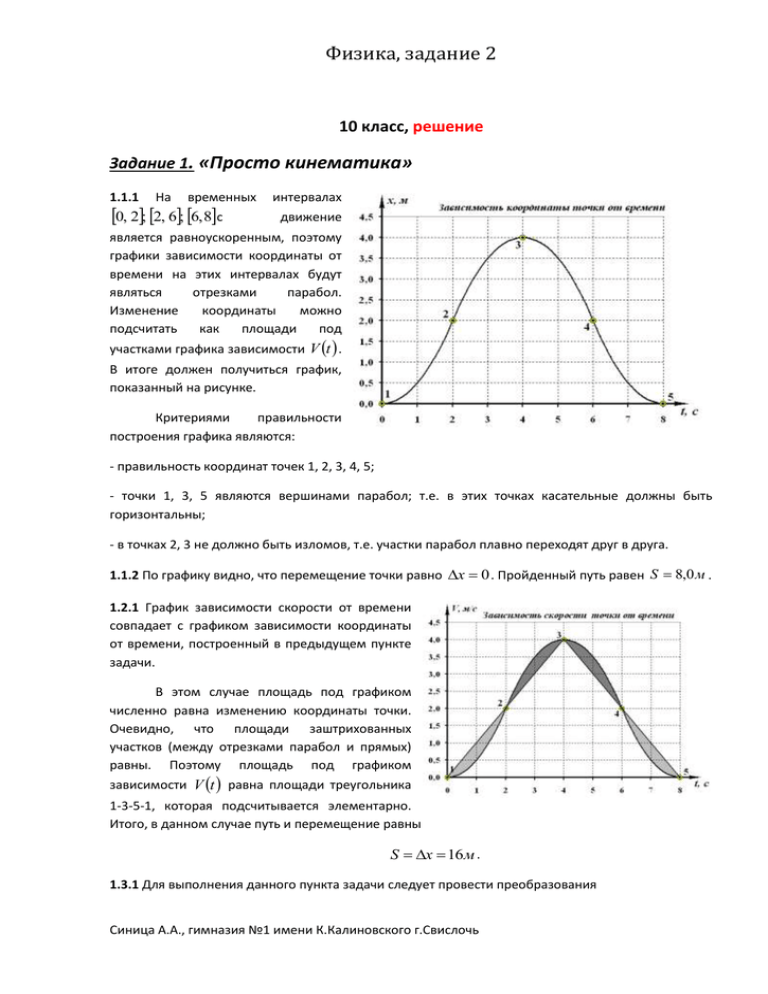
Физика, задание 2
10 класс, решение
Задание 1. «Просто кинематика»
1.1.1
На
временных
0, 2; 2, 6; 6, 8с
интервалах
движение
является равноускоренным, поэтому
графики зависимости координаты от
времени на этих интервалах будут
являться
отрезками
парабол.
Изменение
координаты
можно
подсчитать
как
площади
под
участками графика зависимости V t  .
В итоге должен получиться график,
показанный на рисунке.
Критериями
правильности
построения графика являются:
- правильность координат точек 1, 2, 3, 4, 5;
- точки 1, 3, 5 являются вершинами парабол; т.е. в этих точках касательные должны быть
горизонтальны;
- в точках 2, 3 не должно быть изломов, т.е. участки парабол плавно переходят друг в друга.
1.1.2 По графику видно, что перемещение точки равно x  0 . Пройденный путь равен S  8,0 м .
1.2.1 График зависимости скорости от времени
совпадает с графиком зависимости координаты
от времени, построенный в предыдущем пункте
задачи.
В этом случае площадь под графиком
численно равна изменению координаты точки.
Очевидно, что площади заштрихованных
участков (между отрезками парабол и прямых)
равны. Поэтому площадь под графиком
зависимости V t  равна площади треугольника
1-3-5-1, которая подсчитывается элементарно.
Итого, в данном случае путь и перемещение равны
S  x  16 м .
1.3.1 Для выполнения данного пункта задачи следует провести преобразования
Синица А.А., гимназия №1 имени К.Калиновского г.Свислочь
Физика, задание 2
V  60
миль
1609 м
м
 60
 27 .
час
3600с
с
Обращаем внимание на правильность округления (в соответствии с точностью исходных данных) –
до двух значащих цифр!
1.3.2 В этом пункте цепочка «пересчета» имеет вид
км
1000 м
2600
~ V
час 
3600с  2,19 Мах
V  
м
м
c
330
330
с
с
2600
В данном случае результат должен быть округлен до трех значащих цифр.
1.4.1 В требуемых координатах график
имеет вид полуокружности.
1.4.2 В данных единицах измерения
пройденный путь равен площади под
графиком, т.е.

. Далее следует перейти в
2
систему СИ. Единицей измерения длины в
используемой «безразмерной» системе
единиц является V0 , поэтому пройденный путь (и перемещение) равен
S

2
V0 .
1.4.3 На графике зависимости скорости от времени ускорение численно равно коэффициенту
наклона касательной. В данном случае касательная перпендикулярна радиусу окружности,
проведенному в точку касания. Из рисунка следует, что коэффициент наклона касательной АС
равен тангенсу угла ОАС, взятому с противоположным знаком, то есть в используемых единицах
~
~
OB
t
t
~
,
a 
 ~~ 
~
AB
V t 
1 t 2
~
здесь V 
V ~ t
, t  . Для перехода в систему единиц СИ необходимо учесть, что единицей

V0
измерения ускорения является величина
V0
2
. Окончательно получаем
Синица А.А., гимназия №1 имени К.Калиновского г.Свислочь
Физика, задание 2
V
V
a  02 a~   02


~
t
1 ~
t2
t


V0

2
1
t2
.
2
Задание 2 «Кастрюля»
1. В каждом случае вода нагревается на T  5  C . Температурный интервал достаточно
маленький. Поэтому можно считать, что мощность тепловых потерь в окружающую среду остается
практически неизменной в этом интервале. Для большей точности в формулу теплопотерь
P   T  T0 
(1)
будем подставлять среднее значение температуры. В нашем случае:
T1  2,5 C
T2  42,5 C
T3  82,5 C
(2).
За некоторый промежуток времени t вода получает от плиты количество теплоты равное Pt
Дж и отдает в окружающую среду количество теплоты равное P t Дж. Уравнение теплового
баланса выглядит следующим образом:
cmT  P  P t
(3).
Подставив выражение для мощности тепловых потерь, запишем уравнение (3) в виде:
cm
T
 P    T  T0 
t
(4).
Преобразуем уравнение (4) к виду:
cm
T
 P  T0    T     T
t
где   P  T0
1.1 Используя данные задачи, можно вычислить значение правой части выражения (5) для
каждого случая, т.е. для каждой средней температуры
(2) найти значение cm
T
. Получим:
t
Синица А.А., гимназия №1 имени К.Калиновского г.Свислочь
Рис.1
(5),
(6),
Физика, задание 2
1.
T1  2,5 C
2.
T2  42,5 C
3.
T3  82,5 C
T
 1235
t1
T
cm
 708
t2
T
cm
 188
t3
cm
(7)
Если мощность теплопотерь действительно пропорциональна разности температур, то все три
точки на графике зависимости cm
T
от T
t
будут находиться на одной прямой. Нетрудно
убедиться, что это действительно так (рис. 1).
1.2 Определим постоянные  и  аналитически:
cm

T
T
 cm
Вт
t1
t3
 13 
T 3  T1
C
  1270 Вт
(8);
(9);
1.3 При нагревании от 20  C до 25 C T  22,5 C . Подставим это значение, а также значения
постоянных  и  в уравнение (5). Получим:
cm
T
    T  978
t x
(10).
Откуда:
t x 
cmT
 64c
978
(11).
1.4 Температура воды перестает изменяться, когда мощность теплопотерь становится равной
мощности плиты. При этом правая часть выражения (5) обращается в ноль. Таким образом,
максимальная температура равна:
Tmax 

 98 C

(12)
2.1 При выключенной плите уравнение теплового баланса будет выглядеть следующим образом:
cm
T
   T  T0    T  T0
t
Синица А.А., гимназия №1 имени К.Калиновского г.Свислочь
(13)
Физика, задание 2
Таким образом, зависимость cm
T
от T и в случае
t
остывания должна быть линейной. Убедимся в этом:
1.
2.
3.
T
 940
t1
T
T2  62,5 C cm
 553
t2
T
T3  32,5 C cm
 160
t3
T1  92,5 C
cm
(14).
Зависимость действительно линейная (рис. 2).
Рис.2
2.2 Можно убедиться, что постоянная  и в этом случае равна:
cm
 
T
T
 cm
t1
t3
 13
T 3  T1
(15).
А постоянная T0 :
T0  263Вт
(16).
Отсюда определяем значение комнатной температуры:
T0  20C
(17).
2.3 При остывании от 50 C до 45 C , средняя температура T  47,5C Подставим известные
величины в уравнение (13) и получим время остывания:
t x 
cmT
 176c
  T  T0
(18).
2.4 Мощность входила в выражение для коэффициента  в первой части задачи (выражение (6)).
Зная комнатную температуру, можно вычислить мощность электроплиты:
P    T0  1,0  103 Вт
(19).
Задание 3. «Чем длина отличается от ширины?»
3.1 Используя известные формулы для сопротивления проводника и параллельного соединения
проводников, найдем требуемое сопротивление
Синица А.А., гимназия №1 имени К.Калиновского г.Свислочь
Физика, задание 2
r
1
1
1  r 2 2 rh
 2 r  2 1 h  





R R1 R2
1 L  2 L 1  2 L
.
R
1  2 L

 r  2 r  2 1 h 
(1)
1 L

 r 2 1  2

1 h 

 2 r 
Ответ может быть представлен и в других эквивалентных формах.
3.2 Используя стандартные формулы, находим
I
U0
R1
.
; U 1  IR1  U 0
R1  R2
R1  R2
(2)
3.3 При подключении дополнительного резистора для расчета силы тока и напряжения можно
воспользоваться полученными формулами (2), в которых вместо величины R1 следует подставить
сопротивление двух параллельных резисторов
R1 
R1 R0
.
R1  R0
(3)
В этом случае напряжение окажется равным
R1 R0
R1  R0
R1 R0
R1
,
U1  U 0
 U0
 U0
R1 R0
R1  R2
R1 R0  R2 R1  R0 
 R2
R1  R0
(4)
а сила тока через амперметр
IA 
U1
R1
.
 U0
R0
R1 R0  R2 R1  R0 
(5)
Если сопротивление резистора R0 велико, то можно пренебречь его проводимостью и считать,
что напряжение на нем совпадает с напряжением, рассчитанным по формуле (2), т.е.
U1  U 0
R1
.
R1  R2
(6)
Сила тока в этом случае оказывается равной
IA 
U 0 R1
.
R0 R1  R2
Синица А.А., гимназия №1 имени К.Калиновского г.Свислочь
(7)
Физика, задание 2
3.4 При решении данного пункта задачи следует
учитывать, что ток течет поперек изоляционного
слоя, причем распределение тока (точнее
плотности тока) вдоль цилиндра не будет
однородным. Так как сопротивление изоляции
велико, то и измеряемый ток будет малым.
Следовательно,
распределение
напряжений
U x  между элементом x цилиндра и хорошо
проводящей трубкой будет примерно таким же,
как при отключенном амперметре, то есть
меняться по линейному закону от U 0 до нуля. Это дает основание использовать в качестве
среднего напряжения между цилиндром и проводящей трубкой среднее арифметическое
напряжений на концах цилиндра, то есть
U0
. Следовательно, измеряемый ток равен
2
I
Где R   
U0
.
2R
(8)
h
- сопротивление изоляционного слоя при протекание тока «поперек».
2 rL
Таким образом, получаем
I
U 0  2 rL
2 h
 
Синица А.А., гимназия №1 имени К.Калиновского г.Свислочь
U 0 rLU 0
.
Ih
(9)