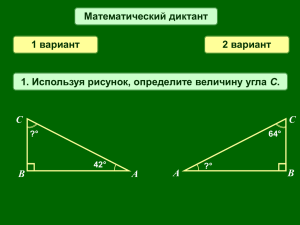
9кл математика 2 четв
реклама
Обязательный образовательный минимум Четверть Предмет Класс II Алгебра, геометрия 9 № Определение п/п (понятие) 1 Определение числовой функции 2 4 5 6 7 8 9 10 Содержание определения (понятия) Если даны числовое множество Х и правило f, позволяющее поставить в соответствие каждому элементу х из множества Х определенное число у, то говорят, что задана функция у = f(х), с областью определения X; пишут:у = f(х), х ∈ 𝑋. При этом переменную х называют независимой переменной или аргументом, а переменную у – зависимой переменной или функцией. значений Множество всех значений функции у = f(х), х ∈ 𝑋, называют областью у = f(х), значений функции и обозначают E(f). Область функции х∈𝑋 Монотонность функции 1. Функцию у = f(х) называют возрастающей на множестве Х, если для любых двух элементов х1 и х2 множества Х, таких, что х1<х2, выполняется неравенство f(х1) <f(х2). 2. Функцию у = f(х) называют убывающей на множестве Х, если для любых двух элементов х1 и х2 множества Х, таких, что х1<х2, выполняется неравенство f(х1) >f(х2). Четная и нечетная 1. Функцию у = f(х), х∈ 𝑋, называют четной, если для любого значения функции х из множества Х выполняется равенство f(–х) = f(х). График четной функции симметричен относительно оси Оу. 2. Функцию у = f(х), х∈ 𝑋, называют нечетной, если для любого значения х из множества Х выполняется равенство f(–х) = – f(х). График нечетной функции симметричен относительно начала координат. Если функция у = f(х) – четная или нечетная, то ее область определения D(f) – симметричное множество. Определение синуса Для любого угла α из промежутка 00 1800 синусом угла α угла α, косинуса называется ордината у точки М, а косинусом угла α — абсцисса х угла α точки М. 0 sin 1, 1 cos 1 Определение Тангенсом угла α (α≠ 90°) называется отношение синуса угла α к тангенса угла α косинусу угла α. Основное sin2 α+cos2 α= 1 тригонометрическое тождество Формулы sin (180̊ – α) = sinα; cos (180̊ – α) = - cosα приведения Таблица значений тригонометрических Угол 0̊ 30̊ 45̊ 60̊ 90̊ 180̊ функций 1 sinα 0 1 0 2 3 2 2 2 cosα 1 3 2 tgα 0 3 3 2 2 1 1 2 3 0 -1 Не существует 0 11 12 13 Теорема о площади Площадь треугольника равна половине произведения двух его сторон на треугольника синус угла между ними. 1 S= absinα 2 Теорема синусов Стороны треугольника пропорциональны синусам противолежащих углов. a b c = = sinA sinB sinC =2R, где R- радиус описанной окружности. Теорема косинусов Квадрат стороны треугольника равен сумме квадратов двух других его сторон минус удвоенное произведение этих сторон на косинус угла между ними. c 2= a 2+b 2− 2 ab ∙ cosC