arccos arcsin arcctg

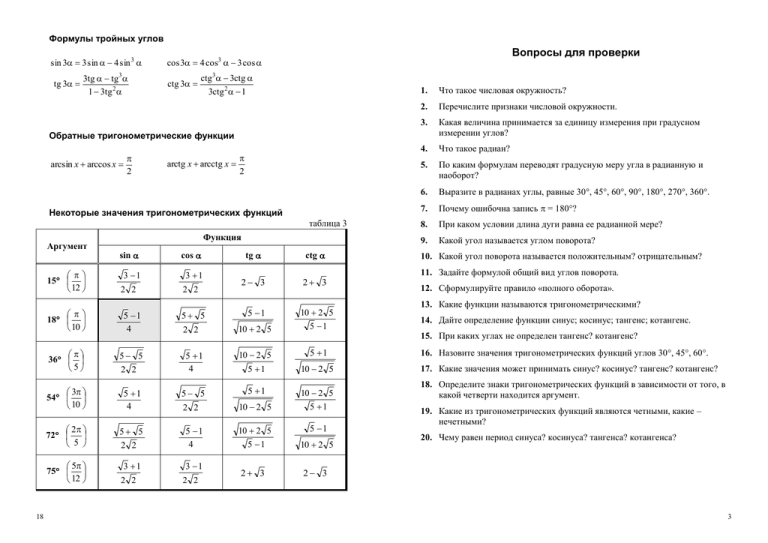
Формулы тройных углов
sin 3  3 sin   4 sin 3 
tg 3 
3tg   tg 3
1  3tg 2 
Вопросы для проверки
cos 3  4 cos3   3 cos 
ctg 3 
ctg3  3ctg 
3ctg 2   1
1.
Что такое числовая окружность?
2.
Перечислите признаки числовой окружности.
3.
Какая величина принимается за единицу измерения при градусном
измерении углов?
4.
Что такое радиан?
5.
По каким формулам переводят градусную меру угла в радианную и
наоборот?
6.
Выразите в радианах углы, равные 30, 45, 60, 90, 180, 270, 360.
7.
Почему ошибочна запись  = 180?
8.
При каком условии длина дуги равна ее радианной мере?
9.
Какой угол называется углом поворота?
Обратные тригонометрические функции

arcsin x  arccos x 
2

arctg x  arcctg x 
2
Некоторые значения тригонометрических функций
таблица 3
Аргумент

15  
 12 
18
Функция
sin 
cos 
3 1
3 1
2 2
2 2
tg 
ctg 
2 3
2 3
10. Какой угол поворота называется положительным? отрицательным?
11. Задайте формулой общий вид углов поворота.
12. Сформулируйте правило «полного оборота».
13. Какие функции называются тригонометрическими?

18  
 10 
5 1
4
5 5
5 1
10  2 5
2 2
10  2 5
5 1

36  
5
5 5
5 1
4
10  2 5
5 1
5 1
10  2 5
17. Какие значения может принимать синус? косинус? тангенс? котангенс?
 3 
54  
 10 
5 1
4
5 5
5 1
10  2 5
18. Определите знаки тригонометрических функций в зависимости от того, в
какой четверти находится аргумент.
2 2
10  2 5
5 1
 2 
72  
 5 
5 5
10  2 5
5 1
2 2
5 1
4
5 1
10  2 5
 5 
75  
 12 
3 1
3 1
2 2
2 2
2 2
2 3
14. Дайте определение функции синус; косинус; тангенс; котангенс.
15. При каких углах не определен тангенс? котангенс?
16. Назовите значения тригонометрических функций углов 30, 45, 60.
19. Какие из тригонометрических функций являются четными, какие –
нечетными?
20. Чему равен период синуса? косинуса? тангенса? котангенса?
2 3
3
1. Числовая прямая
11. Простейшие тригонометрические неравенства
Алгебраические функции — это функции, заданные аналитическим
выражением, в записи которого
используются алгебраические операции
над числами и переменной (сложение,
вычитание, умножение, деление,
возведение в степень, извлечение корня).
zB
у = 2х + 3,
f ( x) 
x
tg  % a

–
– – 

–
2
 = arcsin а
а
х
 = arccos а
–
Error!
 = arctg а
1.
2.
3.
zB
Провести прямую к линии соответствующей функции.
Выделить дугу, на которой лежат решения неравенства.
Найти концы этой дуги, помня, что обход совершается против
часовой стрелки от меньшего числа к большему.
Прибавить к концам интервала числа, кратные периоду функции.
Решить неравенство sin x  
Решение.
1
.
2
Все решения, удовлетворяющие заданному
неравенству, лежат на дуге l. Найдем ее концы:
1

 1
t1  arcsin     arcsin   ,
2
6
 2
 7
 
t 2    t1          
.
6
6
 6
С учетом периода синуса, запишем ответ:

7
  2n  x 
 2n, n  Z .
6
6
Ответ:
7
 

 6  2n; 6  2n , n  Z.


4
а
Чтобы решить простейшее тригонометрическое неравенство нужно:
4.
Признаки числовой прямой:
1) начало отсчета;
2) единичный отрезок;
3) положительное направление (стрелка).
Error!

а
а
2 – 
|а|
1
cos  % a
x 1
Числовая прямая — это математическая модель для представления
чисел, в которой каждое число соответствует
точке на прямой, причем расстояние от точки до
начала отсчета равно модулю числа:
0
sin  % a
l
–
t2
Error!
t1
17
10. Простейшие тригонометрические уравнения
2. Числовая окружность
sin x  a  x   1 arcsin a  n, n  Z
n
Единичная окружность — это окружность, радиус которой принят за
единицу измерения.
cos x  a  x   arccos a  2n, n  Z
tg x  a  x  arctg a  n, n  Z
ctg x  a  x  arcctg a  n, n  Z
Числовая окружность — это единичная окружность с установленным
соответствием между действительными
числами и точками окружности:
При |а| > 1 уравнения s i n x = a
и c o s x = a корней не имеют!
W
1 ед.
2
1
1 ед.
3
NB
Если правая часть уравнения — отрицательное число, то следует
воспользоваться свойствами соответствующих обратных
тригонометрических функций, тогда:

sin x  a  x   1n  1 arcsin a  n, n  Z
 при a  1 !
cos x  a  x    arccos a   2n, n  Z 
tg x  a  x  arctg a  n, n  Z

2
1
0
–1
sin x = 1

x   2n
2
cos x = 1
–1
x  2n
0
sin x = 0
0
0
x  n

 n
2
–1
0
NB
1
0
0


2
sin x = –1

x    2n
2
cos x = –1
x    2n
–2
0
–3
0
1
–4
2
–1
Р
+
0
–
Р–
3
2
2
–1
1
0
4
–2
3
1
2
–1
0
–3
Откладывать можно дуги какой угодно длины. То есть числовую
окружность можно рассматривать как окружность радиуса 1,
на которую «намотана» числовая прямая:
3

х
2
Указанное соответствие можно
определить следующим образом:
каждому числу  соответствует такая
точка Р числовой окружности, чтобы
дуга ОР имела длину || и была
отложена в положительном направлении
если  > 0 и в отрицательном, если  < 0:
4
1
16
x
1
Признаки числовой окружности:
1) начало отсчета – правый конец горизонтального диаметра;
2) единичный отрезок – длина радиуса окружности;
3) положительное направление – против часовой стрелки.
cos x = 0
–1
–1
0

2
1

1
0
5
При а = 1; 0; –1 решение уравнения записывается в виде (n  Z):
0
0
4
ctg x  a  x    arcctg a  n, n  Z
W
–6
6
W
–5
–4
0
–1
0
3
1
0
–1
–2
–3
5
Арксинусом
3. Радианная мера углов и дуг
 
интервала  ;  , синус которого равен а.
 2
Угол в 1 — это центральный угол, опирающийся на дугу, длина
которой равна Error!части окружности.
  
 ;
arccos а

Угол в 1 радиан — это центральный угол, опирающийся на дугу, длина
которой равна радиусу окружности.
0
–1
0
1
1 ед.
1 рад
 рад = 180

1 
180
 
интервала   ;  , тангенс которого равен а.
2 2

0

2
–
–

arctg a 

  
 ; 
 2 2
x
arcctg а
0
  180
9. Обратные тригонометрические функции
1.
ctg x  a
Для отрицательных значений аргумента:
arcsin a    arcsin a
arccos a     arccos a
2.
tg x  a
Арккотангенсом числа а называется такое число х из
интервала (0; ), котангенс которого равен а.
0; 
1. Говорят: «угол Error!радиан» или чаще «угол Error!».
Обозначение «радиан» или «рад», как правило, опускают.
2. Термин «радианное измерение углов» равносилен термину
«числовое измерение углов», т.е. фраза «угол  равен двум
радианам» равносильна фразе «угол  равен числу 2» и даже
«угол  равен двум». Поэтому вопрос типа «Чему равно
Error!?» некорректен. Нужно спрашивать: «Чему равен угол
Error!?» (60) или «Чему равно число Error!?» ( 1,05).
,
а +
arcctg a  x ,
W
NB
Арктангенсом числа а называется такое число х из
0
Для связи радианов и градусов используют развернутый угол:
cos x  a
+
а
arctg а

sin x  a
Арккосинусом числа а называется такое число х из
интервала [0; ], косинус которого равен а.
1; 1 0; 
arccos a  x ,
1
а

2
1 рад  57 ,3  571745
Радианная мера угла численно равна пути,
который проходит точка по дуге единичной
окружности, на которую опирается этот угол:
2
1; 1  2 2 
arcsin a  x ,
Угол поворота — это угол, полученный вращением луча около его
начала О от начального положения ОА до
конечного положения ОВ.
W
числа а называется такое число х из
arctg a   arctg a
arcctg a     arcctg a
Из определения аркфункции сразу следует, что:
sin arcsin a   a 
 где a  [1; 1]
cosarccos a   a 
tgarctg a   a
ctgarcctg a   a

2
6
1
а
0
–1
arcsin а
0
15
VI.
Формулы половинного аргумента (знак – по функции в левой части):

1  cos 
1. sin  
2
2

1  cos 
2. cos  
2
2

1  cos 
sin 
1  cos 
3. tg  


;
2
1  cos  1  cos 
sin 
4. Угол поворота
Полный оборот — это угол поворота, равный 2 рад (или 360).
    2n, n  Z
Угол поворота
это угол
VII.
Формулы сумм:
1.
2.
3.
4.
5.
6.

 
sin   sin   2 sin
cos
2
2
 
 
sin   sin   2 sin
cos
2
2

 
cos   cos   2 cos
cos
2
2

 


cos   cos   2 sin
sin
 2 sin
sin
2
2
2
2
sin(  )

tg   tg  
; ,    n, n  Z
cos  cos 
2
sin(  )
ctg   ctg  
; ,   n, n  Z
sin  sin 
Общий вид
углов поворота
X.
14
Универсальная тригонометрическая подстановка:


2tg
1  tg 2
2
2 ;     2n, n  Z
1. sin  
2. cos  
2 
2 
1  tg
1  tg
2
2
Некоторые дополнительные формулы:
b
1. a sin   b cos   A sin(  ), где A  a 2  b 2 ,   arctg
a






2. cos   sin   2 sin     2 cos   
4

4

Правило
«полного оборота»
t + 2
 = 0 + 360  п
M(t) = M(t + 2k)
Любые два поворота с
конечным положением
0  [0; 360)
отличаются друг от
друга на целое число
полных оборотов
Если точка М числовой
окружности
соответствует числу t,
то она соответствует и
любому числу вида
t + 2k, где k  Z
NB
Некоторые положения конечной точки угла поворота:
VIII. Формулы произведений:
1
1. sin  sin   cos(  )  cos(  ) 
2
1
2. cos  cos   cos(  )  cos(  ) 
2
1
3. sin  cos   sin(  )  sin(  ) 
2
IX.
это число

 1,57
2
0
  3,14

2
3
4
3
 4,71
2

4

5
6
0
5
4
3
2
7
4
2  6,28
2
3

2

3

7
6

6
0
4
3
3
2
5
3
11
6
7
I.
5. Определение тригонометрических функций
1. sin 2   cos 2   1
1
2. 1  tg 2  
;
cos 2 
1
3. 1  ctg 2  
;
sin 2 
Функция косинус — это функция, которая ставит в соответствие
каждому числу t абсциссу точки М(t)
координатной окружности.
Функция синус —
это функция, которая ставит в соответствие
каждому числу t ординату точки М(t)
координатной окружности.
у
Если М(t) = М(х; у),
то х = cos t, у = sin t
4. tg   ctg   1;
М(t)
II.
sin t
t
cos t
Таким образом,
Запись М(t) показывает положение точки М на координатной
окружности, а запись М(cos t; sin t) – положение той же точки на
координатной плоскости.
Функция тангенс — это частное от деления функции синус на
функцию косинус.
Поскольку деление на нуль невозможно, функции tg t и ctg t
определены не для всех значений аргумента. Тангенс определен
лишь для значений аргумента, при которых cos t  0, котангенс
определен при sin t  0:
sin t
, где
cos t
cos t
сtg t 
, где
sin t
tg t 
t

n
, n Z
2
Формулы (теоремы) сложения аргументов:
1. sin(  )  sin  cos   cos  sin 

 n, n  Z
2

 n, n  Z
2
IV.
Формулы двойного аргумента:
1
sin 2
2
2. cos 2  cos2   sin 2   1  2 sin 2   2 cos2   1
1. sin 2  2 sin  cos ,
3. tg 2 
t  k , k  Z
V.
8
  n, n  Z
Формулы приведения:
1) функция меняется на кофункцию при переходе через вертикальную
ось и не меняется при переходе через горизонтальную;
2) перед приведенной функцией ставится знак приводимой функции,
считая  углом первой четверти.

 k , k  Z
2
Тригонометрические функции — это общее название функций синус,
косинус, тангенс и котангенс.

 n, n  Z
2
III.
Функция котангенс — это частное от деления функции косинус на
функцию синус.
W

2. sin(  )  sin  cos   cos  sin 
3. cos(  )  cos  cos   sin  sin 
4. cos(  )  cos  cos   sin  sin 
tg   tg 
5. tg (  ) 
;
, ,    
1  tg  tg 
tg   tg 
6. tg (  ) 
;
, ,    
1  tg  tg 
х
М(t) = М(cos t; sin t)
NB
Основное тригонометрическое тождество и следствия из него:
2 tg 
1  tg 2
отсюда
sin  cos  
4. ctg 2 
Формулы понижения степени:
1
1. sin 2   1  cos 2 
2
1
2
2. cos   1  cos 2 
2
ctg 2  1
2ctg 
1  cos 2
1  cos 2
1  cos 2
2
4. ctg  
1  cos 2
3. tg 2  
13
Значения тригонометрических функций
некоторых углов
таблица 1
0
Error!
0
Error!
sin 
cos 
1
tg 
0
ctg 
Error!
1
2
1
3
2
1
3
—

2
3
3
2
2

2
2

1
–1
0
Error!
0
–1
0
3
—
0
—
3
3π

2
π

2
–
–1
у = sin x
   π
6 4 3 2

3π
2
3

3
3
—
0
0
синусоида
у
–2

3π
2
–

π
2
π
2
–1
у = cos x
Связь между тригонометрическими функциями
одного аргумента

3π
2
х
5π
2
2
косинусоида
у
1
таблица 2
sin 
cos 
sin  =
sin 
 1  cos 2 
cos  =
tg  =
сtg  =
–2
Выражение искомой функции через
Искомая
функция


1  sin 2 
1  sin 2 
sin 

cos 
 1  sin 2 
sin 
tg 



1  tg 
2
1
1  tg 
2
tg 
cos 
1
tg 
1  cos 
2

3π
2
–

π
2
π
2
–1

3π
2
х
5π
2
2
сtg 
tg 
1  cos 
cos 
2
х
2
1
1
1
у
Error!
1
3
2
1
3
Error!
Error!
Тригонометрический набор координат:


1
1  ctg 
2
у = tg x
тангенсоида
у = ctg x
котангенсоида
у
у
2
2
1
1
ctg 
1  ctg 2 
1
ctg 
сtg 
–

π
2
–1
–2
π
2

х

π
2
–1
π
2

3π
2
х
–2
6. Графики тригонометрических функций
12
9
7. Свойства синуса и косинуса
Область
значений
Линия синусов
у
8. Свойства тангенса и котангенса
Знаки по
четвертям
1
1
sin t
+
0
+
0
–
–1
–1
–t
–
Область
значений
Знаки по
четвертям
Четность –
нечетность
у
t
t
cos t
1
х
–1
0
1 –1
–
0
–
+
+
–
1 –1
0
cos t
1
cos(-t)
+ –
|cos t|  1
Область значений
E(cos) = [–1; 1]
нечетная функция
10
tg(-t)
+
+
–
E(tg) = (–; +)
Четность –
нечетность
+
–
Область определения



Dtg  R \   k , k  Z 
2

Область значений
ctg(-t)
0
ctg t
t
–t
ctg(–t) = –ctg t
Dctg  R \ k , k  Z
E(ctg) = (–; +)
Четность – нечетность
четная функция
нечетная функция
Периодичность
sin(x  2) = sin x
0
–
ctg t  (–; +)
Четность – нечетность
–t
tg(–t) = –tg t
+
х
cos(–t) = cos t
D(cos) = R
E(sin) = [–1; 1]
1
t
Область определения
D(sin) = R
0
0
–
Знаки по
четвертям
t
–t
–
tg t
t
0
Область
значений
–1
ctg t
+
tg t  (–; +)
Линия
котангенсов
t
+
–1
–
sin(–t) = –sin t
у
–1
х
–1
–1
–
0
t
sin(-t)
|sin t|  1
Линия косинусов
tg t
Четность –
нечетность
+
1
t
0
–
х
Знаки по
четвертям
+
+
у
t
sin t
Область
значений
Линия тангенсов
1
1
t
t
Четность –
нечетность
нечетная функция
Периодичность
cos(x  2) = cos x
tg(x  ) = tg x
ctg(x  ) = ctg x
11