Исследование риска и доходности

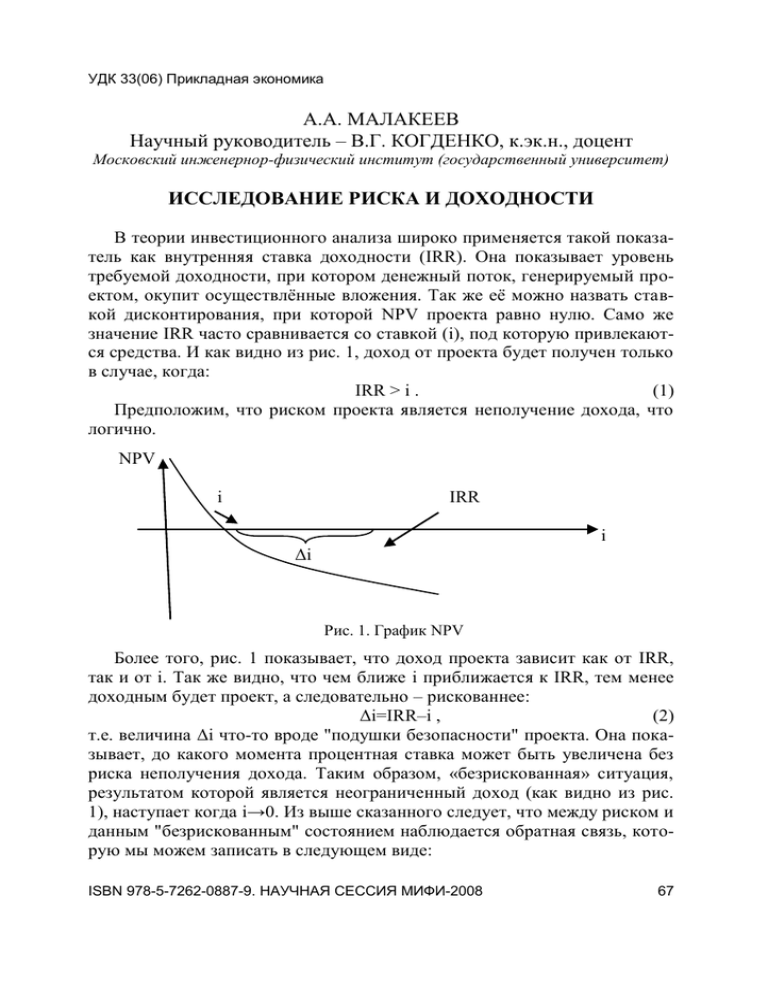
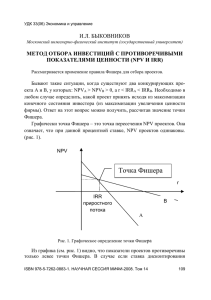
УДК 33(06) Прикладная экономика
А.А. МАЛАКЕЕВ
Научный руководитель – В.Г. КОГДЕНКО, к.эк.н., доцент
Московский инженерноp-физический институт (государственный университет)
ИССЛЕДОВАНИЕ РИСКА И ДОХОДНОСТИ
В теории инвестиционного анализа широко применяется такой показатель как внутренняя ставка доходности (IRR). Она показывает уровень
требуемой доходности, при котором денежный поток, генерируемый проектом, окупит осуществлённые вложения. Так же её можно назвать ставкой дисконтирования, при которой NPV проекта равно нулю. Само же
значение IRR часто сравнивается со ставкой (i), под которую привлекаются средства. И как видно из рис. 1, доход от проекта будет получен только
в случае, когда:
IRR > i .
(1)
Предположим, что риском проекта является неполучение дохода, что
логично.
NPV
i
IRR
i
Δi
Рис. 1. График NPV
Более того, рис. 1 показывает, что доход проекта зависит как от IRR,
так и от i. Так же видно, что чем ближе i приближается к IRR, тем менее
доходным будет проект, а следовательно – рискованнее:
Δi=IRR–i ,
(2)
т.е. величина Δi что-то вроде "подушки безопасности" проекта. Она показывает, до какого момента процентная ставка может быть увеличена без
риска неполучения дохода. Таким образом, «безрискованная» ситуация,
результатом которой является неограниченный доход (как видно из рис.
1), наступает когда i→0. Из выше сказанного следует, что между риском и
данным "безрискованным" состоянием наблюдается обратная связь, которую мы можем записать в следующем виде:
ISBN 978-5-7262-0887-9. НАУЧНАЯ СЕССИЯ МИФИ-2008
67
УДК 33(06) Прикладная экономика
r=1/(IRR–i)=1/Δi .
(3)
При этом для каждого проекта существует своё минимальное значение
риска, оно зависит от значения IRR при i = 0. Таким образом, можно сделать первый вывод: абсолютно безрискованного проекта не бывает. Чтобы r было равно нулю, IRR должно быть бесконечно большим (IRR→∞):
r =Lim1/IRR = 0.
(4)
Для стандартизации значения r мы можем переписать формулу (4) как:
r*IRR = IRR/(IRR - i).
(5)
Таким образом, полученное значение можно назвать модифицированным риском (Mr=r*IRR). Он показывает, какая доля внутренней доходности
приходится на единицу риска, или какая доля IRR работает не на погашения риска, а на получения дохода. Стандартизованной эту формулу можно
назвать потому, что проект с "нулевым" риском имеет значение Mr=1.
Единственным выявленным недостатком является то, что выведенные
коэффициенты не работают, когда процентная ставка равна внутренней
доходности так как знаменатель в этом случае обращается в нуль.
Всё выше описанное подводит нас ко второму выводу, который является центральной идей данной работы: так как доходность проекта существует только когда Δi > 0 или когда IRR > i, а минимальный риск существует, когда Δi→IRR, то получается что: риск проекта находится в обратной зависимости от дохода. Таким образом, наибольший ожидаемый доход проекта будет наибольшим при минимальном риске, а не при
его увеличении.
В конце приведём ещё одно доказательство этой связи. Предположим
мы имеем два портфеля ценных бумаг, портфели А и В. Портфель А имеет значение коэффициента β близкое к +1, а портфель В β близкое к -1.
При этом предположим, что коэффициенты описывают связь портфелей с
каким-нибудь фондовым индексом.
Таким образом, исходя, из традиционных представлений, мы имеем, что
риск портфеля В будет выше риска портфеля А (так как фондовый рынок, как правило, больший период времени находится в фазе роста). А если
так, то и ожидаемая доходность портфеля В будет выше, чем по портфелю А, так как инвесторам требуется надбавка за риск в виде премии.
На самом же деле, несмотря на большую рискованность портфеля
В, его доходность (в том числе ожидаемая) не может быть выше доходности А. Это объясняется тем, что имея отрицательную связь с движением индекса, на долгосрочном промежутке портфель В будет убыточным
(если конечно же в экономике не наблюдается рецессия). Таким образом,
прямая связь между риском и доходностью ставится под сомнение.
ISBN 978-5-7262-0887-9. НАУЧНАЯ СЕССИЯ МИФИ-2008
68
УДК 33(06) Прикладная экономика
ISBN 978-5-7262-0887-9. НАУЧНАЯ СЕССИЯ МИФИ-2008
69