На правах рукописи Специальность 05.13.15 »

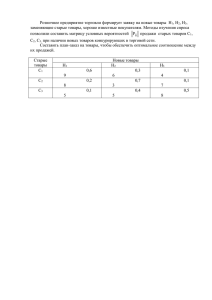
На правах рукописи
Наинг Лин Аунг
ЭФФЕКТИВНОСТЬ ТОЛЕРАНТНОЙ РАСПРЕДЕЛЕННОЙ
ВЫЧИСЛИТЕЛЬНОЙ СИСТЕМЫ ПРИ ВЫПОЛНЕНИИ ДВУХТИПНЫХ
ЗАДАЧ
Специальность 05.13.15
«Вычислительные машины и системы»
АВТОРЕФЕРАТ
диссертации на соискание ученой степени
кандидата технических наук
Москва – 2009
Работа выполнена на кафедре «Вычислительные машины, системы и сети»
Московского
авиационного
института
(государственного
технического
университета, МАИ).
Научный руководитель:
доктор технических наук, профессор
Брехов Олег Михайлович
Официальные оппоненты:
доктор технических наук, профессор
- Сюзев Владимир Васильевич
кандидат технических наук, с.н.с
- Зайко Юрий Григорьевич
Ведущая организация:
- Институт проблем передачи информации ИППИ РАН
Защита состоится « __ » декабря 2009 г. в ___ часов на заседании
диссертационного совета Д 212.125.01 в Московском авиационном институте
(государственном техническом университете, МАИ) по адресу: 125993, г. Москва,
А-80, ГСП-3, Волоколамское шоссе, д.4.
С диссертацией можно ознакомиться в библиотеке Московского авиационного
института (государственного технического университета, МАИ).
Отзывы, заверенные печатью, просьба высылать по адресу: 125993, г.Москва, А-80,
ГСП-3, Волоколамское шоссе, д.4, МАИ, Ученый совет МАИ.
Автореферат разослан «___» ноября 2009 г.
Ученый секретарь
диссертационного совета Д 212.125.01,
кандидат технических наук, доцент
А.В.Корнеенкова
2
ОБЩАЯ ХАРАКТЕРИСТИКА РАБОТЫ
Актуальность темы
Толерантная распределенная вычислительная система (ТРВС) играет
главную роль в решении многих задач в таких областях, как сеть рабочих станций
(выбор процессора для выполнения программы, единая файловая система),
роботизированный завод (роботы связаны с разными компьютерами, но действуют
как внешние устройства единого компьютера), банк с множеством филиалов,
система резервирования авиабилетов. ТРВС - совокупность независимых
компьютеров, которая представляется пользователю единым компьютером.
Производительность вычислительной системы может определяться по
отношению к различным
уровням функционирования, в частности, при
выполнении команд, программ, задач и заданий. В данной работе, имея в виду
ТРВС, производительность соотносится к уровню выполнения задач. Выполнение
задачи возможно при наступлении двух обстоятельств: 1) готовности задачи к
выполнению при возникновении для нее определенного события, например,
связанного с получением входных данных, и 2) наличии свободного ресурса,
например, вычислительного модуля (ВМ). Влияние готовности задачи к
выполнению может быть учтено при иcпользовании модели функционирования
ТРВС как системы с динамическим изменением числа задач [1]. В этом случае
каждая выполненная процессором задача приводит в состояние готовности
некоторое число задач из
максимально подлежащих выполнению. Наличие
свободного ресурса, несомненно, зависит от распределения задач по ВМ, где они
должны выполняться.
В реальных ТРВС времена выполнения задач могут значительно отличаться
так, что задание их посредством экспоненциальной функции распределения с один
и тем же параметром становится не правомочным. Кроме того, вероятности
инициации того или другого числа задач после выполнения одной или другой
задачи так же могут значительно отличаться, что требует использования
отличающихся векторов вероятности инициации задач после выполнения разных
задач.
Таким образом, при более адекватном моделировании реальных РВС
требуется использовать модели задач разного типа, когда тип задачи определяется
своим параметром экспоненциальной функции распределения и своим вектором
вероятности инициации задач после выполнения этой задачи.
В данной работе будут разработаны модели ТРВС с двухтипными
функциональными задачами.
Цель диссертационной работы
Целью диссертационной работы является оценка эффективности ТРВС при
выполнении двухтипных задач.
Поставленная
цель
определяет
следующие
основные
задачи
диссертационной работы:
1.
Определение функционирования ТРВС при выполнении двухтипных задач.
2.
Разработка интегрированной модели производительности гомокопийной
толерантной распределенной вычислительной системы (ГоТРВС) при
3
3.
4.
5.
6.
выполнении
двухтипных
задач
для
стационарного
режима
функционирования.
Разработка интегрированной модели производительности ГоТРВС при
выполнении двухтипных задач для переходного режима функционирования.
Разработка модели производительности гетерокопийной толерантной
распределенной вычислительной системы (ГеТРВС) при выполнении
двухтипных задач для стационарного режима функционирования.
Разработка модели производительности ГеТРВС при выполнении
двухтипных задач для переходного режима функционирования.
Проведение имитационного моделирования ТРВС на основе системы
моделирования GPSS для оценки предлагаемых решений.
Методы исследования
Для решения сформулированных задач использовались методы теории
графов, теории систем массового обслуживания и имитационного моделирования.
Математические модели представлены в виде компьютерных программ на языке
программирования MatLab и математических расчетов в Exсel. Имитационные
модели построены на основе системы моделирования GPSS.
На защиту выносятся следующие положения:
1.
Интегрированная модель производительности ГоТРВС при выполнении
двухтипных задач для стационарного режима функционирования.
2.
Интегрированная модель производительности ГоТРВС при выполнении
двухтипных задач для переходного режима функционирования.
3.
Модель производительности ГеТРВС при выполнении двухтипных задач для
стационарного режима функционирования.
4.
Модель производительности ГеТРВС при выполнении двухтипных задач для
переходного режима функционирования.
Научная новизна
Научная новизна работы состоит в разработке оценки эффективности
толерантной распределенной вычислительной системы при выполнении
двухтипных задач. В ходе выполнения диссертационных исследований получены
следующие новые научные результаты:
1.
Разработана интегрированная модель производительности ГоТРВС при
выполнении
двухтипных
задач
для
стационарного
режима
функционирования.
2.
Разработана интегрированная модель производительности ГоТРВС при
выполнении двухтипных задач для переходного режима функционирования.
3.
Разработана модель производительности ГеТРВС при выполнении
двухтипных задач для стационарного режима функционирования.
4.
Разработана модель производительности ГеТРВС при выполнении
двухтипных задач для переходного режима функционирования.
Достоверность полученных в диссертационой работе результатов подтверждается:
 Корретностью использования адекаватного математического аппратата;
4
 Апробацией материалов диссертации;
 Совпадением результатов аналитических и имитационных моделей.
Практическая значимость
1. Определена эффективность толерантной распределенной вычислительной
системы в зависимости от параметров выполняемых двухтипных задач.
Реализация результатов работы
Результаты диссертационной работы используются в учебном процессе
кафедры «Вычислительные машины, системы и сети» Московского авиационного
института (государственного технического университета) при изучении
дисциплины «Моделирование ЭВМ и систем».
Апробация работы
Основные положения и результаты диссертационного исследования
докладывались автором и обсуждались: на XVII международном научнотехническом семинаре (Алушта, 2008г.), на всероссийской конференции молодых
ученых и студентов «Информационные технологии в авиационной и космической
технике» (Москва, 2008г.).
Публикации
Основные материалы диссертационной работы опубликованы в 3 печатных
работах.
Структура и объем диссертации
Диссертация состоит из введения, четырёх глав, заключения,
библиографического списка из 73 наименований и приложения (включающего частей). Работа изложена на 120 страницах, содержит 31 таблиц и 23 рисунка.
СОДЕРЖАНИЕ РАБОТЫ
Во введении основные цели и задачи работы. Рассматриваются реализация
архитектур распределенной вычислительной системы (РВС). Рассматриваются
методы исследований, раскрывается новизна и практическая ценность работы.
В первой главе сформулирована постановка задачи и описание подхода к ее
решению. В дополнение к более высокому уровню вычислительной мощности,
РВС позволяет многим пользователям взаимодействовать открыто. Различные
формы распределенного вычисления учитывают различные уровни открытости.
В [1] предложена интегрированная аналитическая модель оценки индексов
производительности РВС. Модель построена на основе двух моделей: модели
оценки числа виртуальных вычислительных модулей (ВМ), учитывающей
деградацию РВС с течением времени и метод обеспечения ее толерантности, и
модели РВС как системы с динамическим изменением числа отнотипных задач,
время выполнения которых определяется в зависимости от числа BM.
В данной работе будут разработаны модели толерантной РВС с двухтипными
функциональными задачами, на основе которых будет проанализирована
5
эффективность
толерантной распределенной вычислительной системы при
выполнении двухтипных задач.
Во второй главе предлагается метод оценки эффективности гомокопийной (с
одинаковым числом копий для задач первого и второго типов) толерантной
распределенной вычислительной системы (ГоТРВС) при выполнении двухтипных
задач на основе развития, разработанной в [1]
интегрированной модели
толерантной РВС, выполняющей функциональные однотипные задачи.
Разработка модернизированной интегрированной модели предполагает
адаптацию модели числа виртуальных ВМ и разработку новой модели времени
выполнения функциональных задач в зависимости от числа виртуальных ВМ.
Первая модель учитывает деградацию РВС с течением времени и метод
обеспечения ее толерантности. Вторая модель рассматривает РВС как систему с
динамическим изменением числа задач, время выполнения которых определяется в
зависимости от числа BM. Выполнение задачи BM возможно при выполнении
двух обстоятельств: 1) готовности задачи к выполнению по получению входных
данных, и 2) наличии свободного ресурса - вычислительного модуля (ВМ).
Пусть РВС содержит n ВМ, n  1 . Функционирование РВС состоит в
выполнении двухтипных задач, при этом с целью обеспечения отказоустойчивости
одна задача любого типа для своего выполнения требует всегда d вычислительных
модулей ВМ( один виртуальный ВМ содержит d вычислительных модулей ВМ).
Без ограничения общности положим, что максимальное число задач первого
(второго) типа, требующих выполнения, равно n + h1 (n + h2), соответственно.
Выполненная задача i –го (i = 1, 2) типа по завершению инициирует задачи с
векторами вероятности  1 и  2 , соответственно,
 1   10   11   12   111   112   122  1 ,
 2   20   21   22   211   212   222   1,
где
 10
- вероятность того, что после выполнения первого типа задач будет
выполняться 0 задач,
11
- вероятность того, что после выполнения первого типа задач будет
выполняться 1 задача первого типа,
12
- вероятность того, что после выполнения первого типа задач будет
выполняться 1 задача второго типа,
111
- вероятность того, что после выполнения первого типа задач будет
выполняться 2 задачи первого типа,
112 -
вероятность того, что после выполнения первого типа задач будет
выполняться 2 задачи первого типа и второго типа,
122
- вероятность того, что после выполнения первого типа задач будет
выполняться 2 задачи второго типа,
6
 20
- вероятность того, что после выполнения второго типа задач
выполняться 0 задач,
будет
 21
- вероятность того, что после выполнения второго типа задач будет
выполняться 1 задача первого типа,
 22
- вероятность того, что после выполнения второго типа задач будет
выполняться 1 задача второго типа,
 211 -
вероятность того, что после выполнения второго типа задач будет
выполняться 2 задачи первого типа,
 212 -
вероятность того, что после выполнения второго типа задач будет
выполняться 2 задачи первого типа и второго типа,
 222 -
вероятность того, что после выполнения второго типа задач будет
выполняться 2 задачи второго типа,
каждая из которых начинает выполняться при наличии свободного ВМ.
Пусть время  B выполнения ВМ задач первого и второго типов является
случайной величиной с экспоненциальной функцией распределения с параметром
1 и  2 , соответственно.
Для оценки производительности РВС используются различные индексы
производительности. Мы получим решение для подсистемы РВС, на основании
которого определяются различные индексы производительности ВС, в частности,
среднее число задач и среднее время выполнения задач.
Имея ввиду трудность математического исследования нестационарного
режима функционирования системы, с одной стороны, и интерес к
характеристикам системы в условиях, когда система функционирует достаточно
долго, с другой стороны, будем считать, что завершение выполняемой задачи при
отсутствии в этот момент в системе других выполняемых задач обязательно
приводит к инициированию одной и более задач.
Другое условие, которое мы также примем: число существующих задач в
системе не может быть более максимального числа задач первого типа n + h1 и
максимального числа задач второго типа n + h2 .
На рис. 1 представлен фрагмент графа развития выполнения
функциональных двухтипных задач. На рис. 2 (i  n, j  n) ,рис. 3 (i  n, j  n) , рис. 4
(i  1, j  1) , рис. 5 (i  1, j  1) и рис. 6 (i  1, j  2, 2 (первого) и 1 (второго типа) задач
находятся в состоянии ожидания) представлены фрагменты перехода из состояния
(i,j) и в состояние (i,j), соответственно.
7
Рис. 1 Фрагмент графа развития выполнения функциональных двухтипных
задач
i,j-1
i+1,J-1
ij
 20
 22
i,j+1
 21
 222
i+1,j
i+2,j-1
 212
 211
j2
ij
i 1
11
10
i-1,j
12
ij
111
i-1,j+1
 112
i+1,j
122
i,j+1
Рис. 2 Фрагмент переходов из состояния (i,j)
8
i-1,j+2
i,j+1
i-1,j+1
ij
(j+1)

20
j 22
i,j-1
(j+1)21
(j-1)222
i-1,j
j 212
i-2,j+1
(j+1) 211
2
ij
1
(i+1)
10
i11
i+1,j
(i+1)
12
ij
i 112
(i-1)
111
i+1,j-1
i-1,j
(i+1)
122
i+1,j-2
i,j-1
Рис. 3 Фрагмент переходов в состояние (i,j)
10
11
 20
12
20
 22
 21
 222
21
30
 212
 211
2
11
1
11
10
01
12
11
111
02
 112
21
122
12
Рис. 4 Фрагмент переходов из состояния (1,1)
9
03
12
02
2 212
22 21
2 2 20
01
11
111  2 22
1 112
21 10
21 12
21
20
10
Рис. 5 Фрагмент переходов в состояние (1,1)
Рис. 6 Фрагмент переходов в состояние (1+2,2+1)
Ниже представлен фрагмент конечно – разностных уравнений для состояния
(i,j) при i  n и j  n .
10
Pij (t  t )  Pij (t )(e i1t .e  j2t )  Pij (t )((1  e i1t ).e  j2t ). 11  Pij (t )(e i1t .(1  e i2t .). 22 
 Pi 1, j (t )((1  e (i 1) 1t ).e  j2t . 10 )  Pi , j 1 (t )(e i1t .(1  e ( j 1) 2t ). 20 ) 
 Pi 1, j (t )((1  e (i 1) 1t ).e  j2t ). 111)  Pi , j 1 (t )(e i1t ).(1  e ( j 1) 1t ). 222 ) 
 Pi 1, j 1 (t )((1  e (i 1) 1t ).e ( j 1) 2t ). 12 )  Pi 1, j 1 (t )(e (i 1) 1t .(1  e ( j 1) 2t ). 21 ) 
 Pi 1, j 2 (t )((1  e (i 1) 1t ).e ( j 2) 2t ). 122 )  Pi 2, j 1 (t )(e (i 2) 1t .(1  e ( j 1) 2t ). 211) 
 Pi , j 1 (t )((1  e i1t ).e ( j 1) 2t ). 112 )  Pi 1, j (t )(e (i 1) 1t .(1  e  j2t ).). 212 );
Pij (t  t )  Pij (t )(1  (i1  j 2 )t  o(t ))  Pij (t )((i1 t  o(t )). 11 )  Pij (t )(( j 2 t  o(t )). 22 ) 
 Pi 1, j (t )(((i  1) 1 t  o(t )). 10 )  Pi , j 1 (t )((( j  1)  2 t  o(t )). 20 )  Pi 1, j (t )((( i  1) 1 t  o(t )). 111) 
 Pi , j 1 (t )((( j  1)  2 t  o(t )). 222 )  Pi 1, j 1 (t )((( i  1) 1 t  o(t )). 12 )  Pi 1, j 1 (t )((( j  1)  2 t  o(t )). 21 ) 
 Pi 1, j 2 (t )(((i  1) 1 t  o(t )). 122 )  Pi 2, j 1 (t )((( j  1)  2 t  o(t )). 211)  Pi , j 1 (t )((i1t  o(t )). 112 ) 
 Pi 1, j (t )(( j 2 t  o(t )). 212 );
 Pij (t )( (i1  j 2 )t  o(t ))  Pij (t )(i1 t ). 11  Pij (t )( j 2 t ). 22 



  Pi 1, j (t )((i  1) 1 t ). 10 )  Pi , j 1 (t )(( j  1)  2 t ). 20 )  Pi 1, j (t )((i  1) 1 t ). 111)  


( Pij (t  t )  Pij (t )) / t    Pi, j 1 (t )(( j  1)  2 t ). 222 )  Pi 1, j 1 (t )((i  1) 1 t ). 12 )  Pi 1, j 1 (t )(( j  1)  2 t ). 21 )   / t


  Pi 1, j  2 (t )((i  1) 1 t ). 122 )  Pi  2, j 1 (t )(( j  1)  2 t ). 211)  Pi, j 1 (t )(i1 t. 112 ) 

  P (t )( j t ). )  o(t )

2
212
 i 1, j

На основе конечно – разностных уравнений получим систему
дифференциальных и систему обыкновенных уравнений, соответственно, для
переходного и стационарного процесса поведения распределенной ВС.
p (t )
Обозначим i , j - вероятность того, что в момент времени t система
находится в состоянии (i,j), т.е. имеет i инициированных задач первого типа и j
инициированных задач второго типа, p n  i , n  j (t ) , i  1, h1 , j  1, h2 - стационарная
вероятность того, что активны n задач первого типа и n задач второго типа, а i
(первого) и j (второго типа) задач находятся в состоянии ожидания,
p (i )  k , ( n  i )  l (t ) , k  1, h1 , l  1, h2 - стационарная вероятность того, что активны i задач
первого типа и (n-i) задач второго типа, а k (первого) и l (второго типа) задач
находятся в состоянии ожидания.Не уменьшая общности далее положим:
1  k2 , k  1, 1  k , 2  1;
В частном случае при 2  i  j  n  1 , cистема дифференциальных
уравнений для определения вероятностей
pi , j ( t )
11
имеет вид:
Pij  (t )  (ik  j  ik 11  j 22 ) Pij (t )  (i  1)k 10 Pi 1, j (t ) 
 ( j  1) 20 Pi , j 1 (t )  (i  1)k 111Pi 1, j (t )  ( j  1) 222Pi , j 1 (t )  (i  1)k 12 Pi 1, j 1 (t ) 
 ( j  1) 21Pi 1, j 1 (t )  (i  1)k 122Pi 1, j 2 (t )  ( j  1) 211Pi 2, j 1 (t )  (i )k 112Pi , j 1 (t ) 
 ( j ) 212Pi 1, j (t ),2  i  j  n  1;
Для случая, когда число ВМ n=3, система дифференциальных уравнений для
определения вероятностей
pi , j ( t )
в соответствии с графом имеет вид:
1 2 222
01
2  2 20
 1 12
2 2 222
02
 1 122
3  2 20
 1 12
110
3  2  222
03
3  2 20
 1 122  1 12
3 2 212
 1 122 3  2 212
3  2 21
3  2  222
0+1,3
110
110
3 2 212
0,3+1
3  2 20
3 2 211
3  2 21
3  2  222
0+2,3
3  2 20
0+1,3+1
110
3  2 212
0+2,3+1
3 2 211
3  2 212
3  2 21
3 
0+3,3 3   2 222 0+3,3+1
2 20
3 2 212
2  2 21
3 2 212
3  2 21
3 2 211
32 ( 21  211)
3  2  222
0+4,3
3  2 212
0+4,3+1
3 2 ( 20   21   211 )
 2 21
1 2 212
10
1 1 112
1 2 20
11
3  2 21
3  2 21
3  2 21
2  2 222
1,2+1
22 20
2  2 212
1 2 222
22 20
12
112
1 103 2 211
2  2 212
22 21
1+1,2
1 10
2  2 212
112
21
2+1,1
2,1+1
2+1,1+1
2  2 211
1 10
2  2 222
112
1 10
1+1,2+2
1 10
2  2 212
2  2 222
22 20  
1 12
2  2 211
1+3,2+12
1,2+2
2  2 212
22 21
1+2,2+1
2  2 212
22(21 211)
2  2 222
2 2 ( 20   21   211 )
20
1 10
2  2 222
22 21
1+1,2+1 2 
2 20
2  2 212
22 20  
1 12
2  2 211
1+3,2
1 10
2  2 222
22 21
1+2,2
112
2  2 212
22 20
2  2 211
1 10
2  2 212
2  2 222
22 20
1+2,2+2
1 10
2 
22(21 211) 2 212
2  2 222

2 ( 20
  21   211 )
1+3,2+2
2,1+2
2,1+3
2+1,1+2
2+1,1+3
2+2,1
2+2,1+1
2+2,1+2
2+2,1+3
30
3,0+1
3,0+2
3,0+3
3,0+4
3+1,0
3+1,0+1
3+1,0+2
3+1,0+3
3+1,0+4
Рис. 7 Граф переходов, n=3
12
Для изучения поведения вычислительной системы в стационарном случае
получена система обыкновенных уравнений. Обозначим pi, j  lim ..t  Pi, j (t ) вероятность того, что система имеет i инициированных задач первого типа и j
инициированных задач второго типа, p n i , n  j  lim t  Pn i, n  j (t ) , i  1, h1 , j  1, h2 стационарная вероятность того, что активны n задач первого типа и n задач второго
типа, а i (первого) и j (второго типа) задач находятся в состоянии ожидания,
p(i )  k ,( n i ) l  lim t  Pi , j (t ) , k  1, h1 , l  1, h2 - стационарная вероятность того, что
активны i задач первого типа и (n-i) задач второго типа, а k (первого) и l (второго
типа) задач находятся в состоянии ожидания.
В частном случае при 2  i  j  n  1 , система обыкновенных уравнений
для определения вероятностей pi, j  lim ..t  Pi, j (t ) имеет вид:
(ik (1   11)  j (1   22 )) Pij  (i  1)k 10 Pi1, j  ( j  1) 20 Pi , j 1  (i  1)k 111Pi1, j 
 ( j  1) 222Pi , j 1  (i  1)k 12 Pi1, j 1  ( j  1) 21Pi1, j 1  (i  1)k 122Pi1, j 2 
 ( j  1) 211Pi2, j 1  (i)k 112Pi , j 1  ( j ) 212Pi1, j ,2  i  j  n  1;
Для оценки производительности РВС используются различные индексы
производительности. Здесь на основе полученного решения для вероятностей
определяются среднее число задач и среднее время выполнения задач.
Среднее число задач при неограниченном числе вычислительных модулей
равно
1
C=
1
1
1
 1
2
1
1( 11   12 )  2( 111   112   122) 
1
1
2
 1
2
1( 21   22 )  2( 211   212   222) ;
Перепишем это выражение, используя меньшее число параметров:
1
C=
1
1
1
 1
2
2  2 10  ( 11   12 ) 
1
1
1
2
 1
2
2  2 20 )  ( 21   22 );
Отсюда следует, что число задач в условиях неограниченного числа
вычислительных модулей зависит от вероятности отсутствия генерации задач  10 и
 20 и вероятностей генерации двух задач  1 (2)  111   112   122 и  2 (2)   211   212   222
или одной задачи  1 (1)   11   12 и  2 (1)   21   22 .
В условиях ограниченного числа вычислительных модулей,среднее число
задач С является нижней границей числа выполняемых задач.
Среднее число задач при ограниченном числе вычислительных блоков
равно
для задач 1-го типа:
n  2n i 1
n 1
i 0 j 1
l 0
n l  h2 l  h1
C1    jPji   (n  l ) 
i 0
 Pn l  j ,l i ;
j 0
для задач 2-го типа:
n 2 n i 1
n 1
i 0 j 1
l 0
n l  h1 l  h2
C2    jPij   (n  l ) 
i 0
 Pl i ,nl  j ;
j 0
13
для задач 1-го и 2-го типов (суммарно):
n 1n i 1
n 1n i 1
n 1n i 1
i 0 j 0
i 0 j 0
i 0 j 0
C12    (i  j ) Pij  n(1    Pij )  n    (n  (i  j )) Pij ;
Среднее время решения задач:
для задач 1-го типа:
T cp1 
1 C1
;
1 ncp
для задач 2-го типа:
T cp2 
1 C2
;
 2 ncp
Для всех экспериментов примем значение С=1. Рассмотрим ряд случаев.
В частном случае при числе вычислительных модулей n=3, h1 =1, h2 =1, где n + h1 максимальное число задач первого типа, n+ h2 -максимальное число задач второго
типа, имеем следующий набор состояний, (таблица 1):
Таблица 1
01
02
03
2,1+1
2+1,1
+1
2+2,1
+1
1,2+1
1+1,2
+1
1+2,2
+1
1+3,2
+1
2,1+2
2+1,1
+2
2+2,1
+2
0,3+1
0+1,3
+1
0+2,3
+1
0+3,3
+1
0+4,3
+1
1,2+2
1+1,2
+2
1+2,2
+2
1+3,2
+2
2,1+3
2+1,1
+3
2+2,1
+3
3,0+2
3,0+3
3,0+4
3+1,0
+2
3+1,0
+3
3+1,0
+4
0+1,3
0+2,3
0+3,3
0+4,3
10
11
12
1+1,2
1+2,2
1+3,2
20
21
2+1,
1
2+2,
1
30
3+
1,0
3,0+
1
3+1,
0+1
Варианты набора вероятностей
1  10  11  12  111  112  122
 2   20   21   22   211   212   222
 10   11   12   111   112   122  1;  20   21   22   211   212   222  1;
представлены в Таблицах 2 и 3:
Варианты  1
1.1
1.2
1.3
 10
0.15
0.30
0.45
 11   12  11   12 
 20
0.15
0.30
0.45
111 112 122 111  112  122 
0.7
0.4
0.1
Таблица 314
Варианты  2
2.1
2.2
2.3
Таблица 2
 22   21  22   21 
0.15
0.30
0.45
 222  212  211 222   212   211 
0.7
0.4
0.1
0.15
0.30
0.45
Среднее число задач и среднее время решения задач при ограниченном
числе вычислительных блоков n=3 при k  1, 2  1 и вариантов Таблицы (2 и 3)
представлено в Таблицах 4, 5 и 6.
Таблица 4
Индексы
производительности
C1
C2
C1 + C2
C12
Tcp1
Tcp 2
Варианты  1 и  2
1.1,2.1
0.95
0.95
1.90
1.90
0.3167
0.3167
1.1,2.2
0.98
1.02
2.00
2.00
0.3267
0.34
1.1,2.3
0.998
1.082
2.080
2.080
0.3327
0.3607
Таблица 5
Индексы
производительности
C1
C2
C1 + C2
C12
Tcp1
Tcp 2
Варианты  1 и  2
1.2,2.1
1.019
0.9776
1.9966
1.9966
0.3397
0.3259
1.2,2.2
1.01
1.01
2.02
2.02
0.3367
0.3367
1.2,2.3
1.010
1.058
2.068
2.068
0.3367
0.3527
Таблица 6
Индексы
производительности
C1
C2
C1 + C2
C12
Tcp1
Tcp 2
На
рисунке
8
представлен
Варианты  1 и  2
1.3,2.1
1.0796
0.9947
2.0743
2.0743
0.3599
0.3316
1.3,2.2
1.0576
1.0094
2.067
2.067
0.3525
0.3365
1.3,2.3
1.0368
1.0368
2.0736
2.0736
0.3456
0.3456
график15поведения среднего числа задач:
Рис. 8 Среднее число задач C12 при k  1, 2  1 ,n=3 и n=5
В третьей главе предложена аналитическая модель оценки индексов
производительности гетерокопийной (с разным числом копий для задач первого и
второго типов) толерантной распределенной вычислительной системы ГеТРВС с
ограниченным числом вычислительных модулей, предназначенной для выполнения
двухтипных задач при динамическом изменении их числа. Рассматривается
переходной и стационарный режим функционирования вычислительной системы.
Пусть РВС содержит n ВМ, n  1. Функционирование ВС состоит в
выполнении двухтипных задач, при этом задача i –го (i = 1, 2) типа для своего
выполнения требует di ВМ.
Как и в главе (2) введем определения. Максимальное число задач первого
(второго) типа, требующих выполнения, равно n  h1 ( n  h2 ), соответственно.
Выполненная задача i –го (i = 1, 2) типа по завершению инициирует задачи, с
векторами вероятности  1 и  2 , соответственно.
Каждая инициированная задача начинает выполняться при наличии
свободного ВМ, иначе она становится в очередь к ВМ.
Пусть время  B выполнения ВМ задач i –го (i = 1, 2) типа является случайной
величиной с экспоненциальной функцией распределения с параметром 1 и  2 ,
соответственно.
Другое условие, которое мы также примем: число существующих задач в
системе не может быть больше максимального числа задач первого типа n  h1 и
максимального числа задач второго типа n  h2 .
При разработке аналитической модели оценки производительности
вычислительной системы с ограниченным числом вычислительных модулей,
предназначенной для выполнения двухтипных задач с динамическим изменением
их числа, рассмотрим переходной и стационарный режим функционирования.
Пусть всегда d1
> d2, не умоляя общности. Тогда для индексов i и j
справедливы неравенства:
16
n
 n 
0  i     1,0  j     1, id1  jd2  n  d1 ;
 d1 
 d2 
n
P  n  id  ,0  i    .
1
i, 

 d1 
 d2 
Обозначим m  n  id1  [
n  id1
]d 2 , в силу того, что d1
d2
> d2
,
следует
m  d 2  1 . Отсюда следует , что по завершению обработки задачи 1-го типа
освобождается d1 вычислительных модулей, поэтому они могут быть
 m  d1 
 задач 2-го типа.

m  d1
m  d2
],   [
];
Обозначим   [
d2
d1
1, если..s   
Пусть также  s ,  

0, если..s   
1, если..s   
 s ,  

0, если..s   
использованы для обработки 
 d2
В частном случае при 0  i 
 m  d1 
m  d2 
 n  i.d1 
n
,  
,   
, m  n  i.d1  
.d 2 , d1  3, d 2  2 ,
d1
 d2 
 d1 
 d2 
cистема дифференциальных уравнений для определения вероятностей pi,  n (i*d1 )  (t)

имеет вид:
d2

P
 n  ( i*d1 ) 
( i ),( 
)
 d2

 (t )  (ik  j  ik  j ) P
11
22
 n  ( i*d1 ) 
( i ),( 
)
 d2

 (i  1)k 10 P
 n  ((i 1)*d1 ) 
( i 1),( 
 ) 1
d2


(t ). 1,  (
(t )  (i )k 10 P
 n  ( i*d1 ) 
( i ) 1, ( 
)
 d2

(t ) 
n  (i * d 1 )
) 20 P  n (i*d )  (t ) 
1 ) 1
d2
i ,( 


d2

n  ((i  1) * d 1 )
n  (i * d 1 )
(
) 20 P
 1) 222 P n (i*d1 ) (t ) 
n  ((i 1)*d1 ) (t ). 1,  (i  1) k 111P
n  ( i*d1 ) (t )  (
( i 1) 1, (
)
i 1,
i,
1
d2
d2
d
d
d
2
2
2
n  (i * d 1 )
 (i  1)k 12 P n ((i )*d1 ) (t )  (
 1) 21 P n (i*d1 ) (t ). 1,  (i  1)k 122 P n (i*d1 ) (t ). 2, 
i 1,
1
i 1,
1
i 1,
2
d2
d
d
d
2
2
2
n  (i * d 1 )
n  (i * d 1 )
(
 1) 211P n (i*d1 ) (t )  (i )k 112 P n  (i*d1 ) (t )  (
) 212 P n  (i*d1 ) (t ) 
i  2,
1
i,
1
i 1,
d2
d2
d
d
d
2
 (i )k 12 P
( i ) 1,
(
n  ((i )*d1 ) (t ). 2,
1
d2
2
 (i  1)k 12 P
( i 1),(
2
(t ). 2,
n  ((i 1)*d1 )
) 1
d2
 (i  1)k 10 P
 n  ((i 1)*d1 ) 
( i 1),( 
)2
d2


(t ). 2, 
n  (i * d 1 )
) 20 P  n (i*d )  (t ). 1,  (i  1)k 122 P n (i*d1 ) (t ),
1 )
i 1,
2
d2
i ,( 

d

d2

2
n
0i
, P( 1) 1, n2 1  P1, n2 1  P 2, n2 1  P1, n2  Pn1 1,( 1) 1  Pn1 1, 1  Pn1 , 1  Pn1 1, 2  0,
d1
 m  d1 
m  d2 
 n  i.d 1 
,   
, m  n  i.d 1  
.d 2 , d 1  3, d 2  2;
 d2 
 d1 
 d2 

Среднее число задач и среднее время решения задач при ограниченном
числе вычислительных блоков n=9 при k  1,  2  0.5 и вариантов Таблицы (2 и 3)
представлено в Таблицах 7,8 и 9.
Таблица 717
Индексы
Варианты  1 и  2
производительности
1.1,2.1
1.1,2.2
1.1,2.3
C1
0.6233
0.6556
0.6756
C2
1.2846
1.4307
1.5451
C1 + C2
1.9079
2.0863
2.2207
C12
1.9079
2.0863
2.2207
Tcp1
0.2078
0.2185
0.2252
Tcp 2
0.3212
0.3577
0.3863
Таблица 8
Индексы
Варианты  1 и  2
производительности
1.2,2.1
1.2,2.2
1.2,2.3
C1
0.6917
0.6907
0.6873
C2
1.3817
1.4599
1.5357
C1 + C2
2.0734
2.1506
2.223
C12
2.0734
2.1506
2.223
Tcp1
0.2306
0.2302
0.2291
Tcp 2
0.3454
0.365
0.3839
Таблица 9
Индексы
Варианты  1 и  2
производительности
1.3,2.1
1.3,2.2
1.3,2.3
C1
0.7529
0.7321
0.7102
C2
1.459
1.493
1.537
C1 + C2
2.2119
2.2251
2.2472
C12
2.2119
2.2251
2.2472
Tcp1
0.251
0.244
0.2367
Tcp 2
0.3648
0.3733
0.3843
В четвертой главе проведена18обобщенная имитационная модель
РВС на основе системы моделирования GPSS для оценки производительности
системы и время выпонения моделирования.
При сравнении с аналитическим методом моделирования для значений
параметров: 1  1,  2  1, 10  0.30, 11  0.20, 12  0.20, 111  0.10, 112  0.10, 122  0.10;
 20  0.15, 22  0.35, 21  0.35, 222  0.05, 212  0.05, 211  0.05; подсчитано среднее число
задач при ограниченном числе вычислительных блоков: С12=1.983, в то время как в
аналитическом методе получено С12=1,9966, т. е. результаты, полученные
аналитическим методом моделирования и моделирование в среде GPSS,
практически совпадают.
При оценке производительности системы с разным количеством
вычислительных блоков получено:
Таблица 10
Модуль Время выполнения
3
83.1378
5
58.1142
7
49.5697
9
31.4671
Основные научные и практические результаты диссертационной работы
Толерантная распределенная вычислительная система (ТРВС) играет
главную роль в решении многих задач.
Производительность ТРВС может определяться по отношению к различным
уровням функционирования, в частности, при выполнении команд, программ, задач
и заданий. В данной работе, имея в виду ТРВС, производительность соотносится к
уровню выполнения задач.
Предложенная в работе аналитическая модель оценки индексов
производительности ТРВС учитывает как число вычислительных модулей (ВМ)
занятых выполнением функциональных задач в зависимости от средств
обеспечения толерантности и времени функционирования ВС, когда ВМ выходят
из строя, и модели ВС как системы с динамическим изменением числа задач,
время выполнения которых определяется в зависимости от числа BM.
Выполнение задачи возможно при наступлении двух обстоятельств: 1)
готовности задачи к выполнению при возникновении для нее определенного
события, например, связанного с получением входных данных, и 2) наличии
свободного ресурса, например, вычислительного модуля (ВМ). Влияние готовности
задачи к выполнению может
быть учтено при использовании модели
функционирования ТРВС как системы с динамическим изменением числа задач
[1]. В этом случае каждая выполненная процессором задача приводит в состояние
готовности некоторое число задач из максимально подлежащих выполнению.
Наличие свободного ресурса, несомненно, зависит от распределения задач по ВМ,
где они должны выполняться.
В реальных ТРВС времена выполнения задач могут значительно отличаться
так, что задание их посредством экспоненциальной функции распределения с один
и тем же параметром становится не правомочным. Кроме того, вероятности
инициации того или другого числа задач после выполнения одной или другой
задачи так же могут значительно19отличаться, что требует использования
отличающихся векторов вероятности инициации задач после выполнения
разных задач.
Таким образом, при более адекватном моделировании реальных РВС
требуется использовать модели задач разного типа, когда тип задачи определяется
своим параметром экспоненциальной функции распределения и своим вектором
вероятности инициации задач после выполнения этой задачи.
В работе разработаны модели ТРВС с двухтипными функциональными
задачами в условиях, когда число копий одинаково для разнотипных задач
(гомокопийная модель производительности ГоТРВС) и когда число копий различно
для разнотипных задач (гетерокопийная модель производительности ГеТРВС).
Таким образом в работе:
1.
Разработана интегрированная модель производительности ГоТРВС при
выполнении
двухтипных
задач
для
стационарного
режима
функционирования.
2.
Разработана интегрированная модель производительности ГоТРВС при
выполнении двухтипных задач для переходного режима функционирования.
3.
Разработана модель производительности ГеТРВС при выполнении
двухтипных задач для стационарного режима функционирования.
4.
Разработана модель производительности ГеТРВС при выполнении
двухтипных задач для переходного режима функционирования.
5.
Определена эффективность толерантной распределенной вычислительной
системы в зависимости от параметров выполняемых двухтипных задач.
Публикации по теме диссертации
1.
2.
3.
Брехов О. M., Наинг Лин Аунг. Оценка производительности распределенной
вычислительной среды при выполнении разнотипных задач. //Труды XVII
международного научно-технического семинара. Сентябрь 2008г., Алушта. –
Редакционно-издательский центр ГУАП, с. 189.
Наинг Лин Аунг. Производительность распределенной вычислительной
среды при выполнении разнотипных задач. //Всероссийская конференция
молодых ученых и студентов «Информационные технологии в авиационной
и космической технике-2008». 21-24 апреля 2008г.Москва. Тезисы докладов.М.:Изд-во МАИ-ПРИНТ, 2008. - 123 с.
Брехов О. M., Наинг Лин Аунг. Модель оценки индексов
производительности вычислительной сети при выполнении разнотипных
задач. //Журнал «Вестник МАИ» 2009г. Т.(16), №(3), с. 101-109.
20
Тираж 100 экз
Отпечатано в Московском авиационном институте
(государственном техническом университете)
г. Москва, А-80, ГСП-3, Волоколамское шоссе, д. 4.
http://www.mai.ru/