КВАНТИЛЬНАЯ МОДЕЛЬ ТЕНЕВОЙ ЭКОНОМИКИ Сибирского

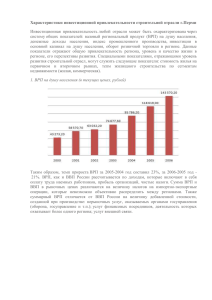
КВАНТИЛЬНАЯ МОДЕЛЬ ТЕНЕВОЙ ЭКОНОМИКИ СИБИРСКОГО
ФЕДЕРАЛЬНОГО ОКРУГА
Долгунов Я.Н., Котежеков В.С.
Науч. руководитель: доктор физ.-мат. наук, профессор Дмитриев Ю.Г.
Томский государственный университет, ТНЦ СОРАН
1. Проблема теневой экономики охватывает все сферы жизнедеятельности
общества. Теневая экономика представляет собой трудный для исследования предмет;
это феномен, в существовании которого можно не сомневаться, но невозможно точно
измерить, т.к. практически вся информация, которую удаётся получить, является
конфиденциальной и разглашению не подлежит.
В различных странах используют разные термины. Под теневой экономикой будем
понимать ненаблюдаемую экономику, включающую в себя как нелегальные виды
экономической деятельности, так и сферу деятельности, часть которой является
абсолютно легальной, но в силу нецелесообразности или несовершенства методологии
статистического наблюдения не является объектом регистрации и учета со стороны
органов государственной статистики [1].
Статистическое изучение теневой экономики актуально для разработки и
эффективной реализации стратегических управленческих решений экономического,
социального и правового характера, оно становится одним из приоритетных
направлений
совершенствования
методологии
экономического
анализа,
макроэкономических измерений.
Существует множество подходов к определению теневой и неформальной
экономики. Большинство подходов основывается на анализе ряда макроэкономических
показателей [1], или на использовании различных инструментов обработки
статистической информации [2]. Авторами предлагается новый метод оценивания
масштаба ненаблюдаемой экономики, который основан на математических моделях
растущих систем [3], т.е. систем, образовавшихся путём последовательного накопления
«вещества» [4].
2. В работе рассматривается применение квантильной модели накопления [3].
Анализу подвергается валовой региональный продукт (ВРП) по субъектам Сибирского
федерального округа за 1998 г. [5].
Предполагается, что в рамках квантильной модели структура ВРП представляет
собой совокупность стоимостных выражений производств услуг и материальных благ.
В силу неоднородности экономики Сибирского федерального округа, существует
приоритетность производства ВРП по субъектам при создании этой совокупности.
В нашей совокупности имеется n объёмов ВРП, соответствующих данным
субъектам. Однако, исходя из неполноты этой совокупности, предположим, что
существуют неучтённые объёмы ВРП, которые дополняют представленную
совокупность. Эти объёмы обуславливают значения ВРП, произведённые в неучтённых
источниках Сибирского федерального округа. Масштаб ненаблюдаемой экономики
может отражаться в неучтённых объёмах ВРП.
Пусть Qi – объем ВРП для i-го субъекта Сибирского федерального округа, i 1, n
Мы исходим из того, что Qi являются случайными величинами, тогда они
подчиняются некоторому закону распределения F(x).
Вследствие приоритетности, упорядочим данные по возрастанию.
Q (i ) - упорядоченные по возрастанию значения объёма ВРП.
Выберем в качестве F(x) класс сдвигово-масштабного семейства, и запишем
соотношение
Q  
F (Qi ) = F0  i
 , i 1, n



где  -параметр сдвига,  -параметр масштаба.
Известно, что если F - истинная функция распределения, то выполняется:
Q  
F0  i
  ui , i 1, n



где ui - равномерно распределённые в [0,1] случайные величины.
Отсюда следует, что математическое ожидание [5]
Q  
i
,
EF0  (i )
  Eu(i ) 
  
n 1


(1)
(2)
Пользуясь соотношением (2) можем записать:
 Q(i )   
  p   , где  -ошибка наблюдения, pi  i
F0 
i
i
i
  
n 1


Таким образом, значения объёмов ВРП Q(i ) удовлетворяет функции регрессии вида:
Q(i )     x(i )   *(i ) ,
(3)
где x(i )  F01  pi  - квантили заданного закона распределения уровня pi ,  *(i ) ошибка наблюдения, M  *(i )  0 .
Применяя метод наименьших квадратов (МНК) к (3), получим оценки параметров
̂ и ̂ . По этим оценкам построим регрессию вида:
Qˆ (i )  ˆ  ˆ x(i )
(4)
Среднеквадратическое отклонение (СКО) линии регрессии от исходных данных
вычисляется по формуле
2
n

ˆ
  Q(i )  Q(i ) 
 .
CKO  i 1 
(5)
n
В работе [7] было показано, что для рассмотренных сдвигово-масштабных
распределений наименьшее СКО будет достигается при логнормальном законе
распределения, поэтому все дальнейшие исследования мы будем проводить для него.
Функция логнормального закона распределения записывается в виде
F  x   (ln x) ,
где ( x) - функция распределения стандартного нормального распределения.
3. Задача оценивания неучтённых объёмов ВРП Сибирского федерального округа,
неотражённых в статистическом отчёте, будет решаться следующим образом.
Предполагается, что объёмы ВРП, связанные с теневой экономикой, дополняют
исходную совокупность до полной, состоящей из N элементов, число которых
неизвестно. В реальности нам известна только часть полной совокупности
Q(1)  Q(2) ...  Q(n) , имеющая n<N элементов. Число неизвестных элементов (N-n) и их
величины требуется оценить. Алгоритм решения этой задачи состоит в следующем.
Исключается из рассмотрения одно значение из исходной совокупности, т.е.
значение ВРП субъекта. В ходе действия алгоритма это значение должно получить
прогноз.
Последовательно увеличивается число элементов совокупности. Так как при этом
увеличивается и число уровней pi , а число исходных данных прежнее, то находится
наилучшее соответствие между новыми квантилями и исходными данными объёмов
ВРП. При увеличении совокупности на единицу сумма квадратов отклонений (СКО)
или сумма модулей ошибок (СМО) на каждом шаге будет уменьшаться. Число
элементов совокупности, при котором происходит смена сильного уменьшения СКО
или СМО на слабое, выбирается за объём полной совокупности N.. Далее по этому
соответствию квантилей и исходных данных строится регрессия (4) и прогнозируется
величины неучтённых объёмов ВРП по оставшимся квантилям. Полученные значения
можно интерпретировать как составные части ненаблюдаемой экономики.
4. Применим описанную выше модель для оценки ненаблюдаемой экономики
Сибирского федерального округа [5]. В качестве исходных данных возьмём:
T
Q  1528 1958 8159 11140 12860 20290 21370 26860 34400 42890 50420 70150

Исключим из рассмотрения одно значение из исходной совокупности Q, равное
26860. Оно представляет собой объём ВРП Омской области.
Применяя алгоритм нахождения неучтённых объёмов ВРП, получим наилучшее
соответствие исходных данных и квантилей полной совокупности, количество
элементов которого N=15. Этот факт иллюстрирует рисунок 1.
4
3
Di
2
1
1
2
3
4
5
6
i
Рисунок 1 – График зависимости среднеквадратического отклонения от числа
добавленных значений объёмов ВРП. Здесь i-количество добавленных значений
объёмов ВРП, а D-величина СКО представленной совокупности.
После этого определяются оценки параметров ̂ и ˆ при помощи МНК и строится
регрессия вида (4), отображённая на рисунке 2.
Рисунок 2 - График линии регрессии для полной совокупности данных.
Здесь Q1-прямая, аппроксимирующая исходные данные, Q2-исходные данные, TYнеучтённые объёмы ВРП, x1-квантили заданных уровней.
Неучтённые объёмы ВРП имеют следующие значения: 5572, 15858, 27961, 103767
млн. руб. Отметим, что найденный объём ВРП равный 27961 представляет собой
прогноз объёма ВРП Омской области, равного 26860.
Таким образом, значения объёмов ВРП 5572, 15858, 103767 млн. руб. представляют
собой составные части неучтённого ВРП, они и составляют масштаб теневой
экономики Сибирского федерального округа согласно квантильной модели.
Литература
1.
Рябушкин
Б.Т.,
Чурилова
Э.Ю.
Методы
оценки
теневого
и
неформального секторов экономики. М.:Финансы и статистика,2003.
2. Бокун Н.Ч. Использование многомерной выборки для измерения
неофициальной экономики // Вопросы статистики. 2008. №2. С.30-37.
3. Дмитриев Ю.Г., Устинов Ю.К. Математические модели растущих систем
// Вычислительные технологии. 2007. том 12. С.68-75.
4. Алексеев Ф.Н. Новые идеи в учении о месторождениях полезных
ископаемых. Томск: Издательство политехнического университета, 2000. 227 C.
5. Таблица [Электрон.ресурс]. Режим доступа - http://www.gks.ru/stat
свободный.
6. Гумбель Э. Статистика экстремальных значений. М: Мир, 1965. 450 C.
7. Котежеков В.С. Курсовая работа. Оценивание параметров теневой
экономики. 2007г.