Задача 1.
реклама

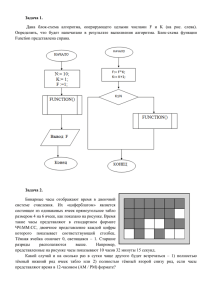
Задача 1. Дана функциональная схема. На вход схемы подаются тройки X, Y, Z в лексикографическом порядке, начиная с 000 и заканчивая 111. Последовательность выходных сигналов представляет собой двоичную запись некоторого числа F. Какой вид будет иметь F в шестнадцатеричной системе счисления? x & F(x, y, z) y 1 z & Задача 2. Бинарные часы отображают время в двоичной системе счисления. Их «циферблатом» является состоящее из одинаковых ячеек прямоугольное табло размером 4 на 6 ячеек, как показано на рисунке. Время такие часы представляют в стандартном формате ЧЧ:ММ:СС, двоичное представление каждой цифры которого показывает соответствующий столбец. Тёмная ячейка означает 0, светящаяся – 1. Старшие разряды располагаются выше. Например, представленные на рисунке часы показывают 10 часов 32 минуты 15 секунд. Какой случай и на сколько раз в сутки чаще другого будет встречаться – 1) полностью тёмный второй снизу ряд ячеек табло при 12-часовом (AM / PM) формате отображения времени или 2) таковой при 24-часовом формате? Задача 3. Представьте себе, что перед вами шахматная доска 26*26. Выберите 2 клетки таким образом, что 1) первая клетка автоматически зачеркивает все клетки этого цвета по вертикали и горизонтали; 2) одну и ту же клетку нельзя использовать два раза; 3) зачеркнутые клетки нельзя использовать. Сколько вариантов выбрать клетки? Задача 4. Хакерам, заключенным в тюрьму, была передана инструкция для побега. Но при передаче были перепутаны местами части инструкции: при правильном расположении частей инструкции хакеру из первой камеры должна попасть часть «А», хакеру из второй камеры — часть «Б» и т.д. Каждый день у заключенных, находящихся в соседних камерах, выпадает возможность обменяться частями плана, но обмениваться более, чем один раз в день слишком рискованно. (Например, если порядок частей переданной инструкции был ВГБА, то для того, чтобы собрать правильную инструкцию АБВГ потребуется 5 дней). Определить, сколько дней потребуется для того, чтобы собрать верную инструкцию, из следующей последовательности: КИЖАБ3ДЕГВ. Задача 5. Имеются три стола A, B, и C с ячейками, в которых размещаются карточки с цифрами. В самом начале все карточки расположены на столе A, требуется переместить их на стол C. Предположим, что есть робот, который может выполнять три инструкции: X) Взять самую левую карточку со стола A и положить ее в самую правую из свободных ячеек стола С. Y) Взять самую левую карточку со стола A и положить ее в самую правую из свободных ячеек стола B. Z) Взять самую левую карточку со стола B и положить ее в самую правую из свободных ячеек стола С. Пусть в ячейках стола A расположены карточки: 8,6,4,2,9,7,5,3. Требуется написать такую инструкцию для робота, при которой в ячейках стола C будет сформировано наибольшее возможное число. Например, пусть на столе A лежат карточки с числами 2, 6, 8, 9. Тогда при выполнении инструкций YYYXZZZ будут произведены следующие действия: A B C 2689 Выполнить 9 YYY 268 Выполнить X Выполнить ZZZ 268 9 9268