Дан вектор конечсного продукта произсодства, Y

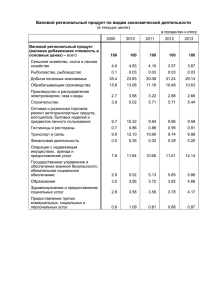
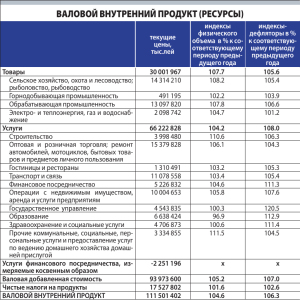
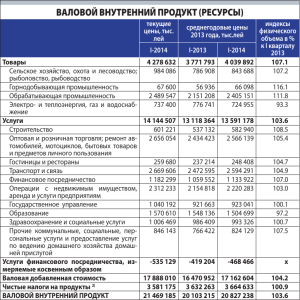
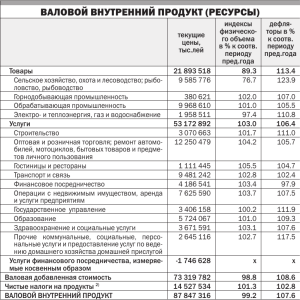
КАФЕДРА МАТЕМАТИКИ
Статична модель міжгалузевого баланса
Бердянськ 2012
I
баланса
ПОСТАНОВКА
и
анализом
Решение задач, связанных с составлением межотраслевого
производительностей
начинается
с
рассмотрения
простой
макроэкономической модели, предполагающей наличие всего двух секторов экономики:
производители и потребители. Производители представлены тремя отраслями, каждая из
которых в то же время является и потребителем производимой продукции. Анализ работы
подобного многоотраслевого производства с помощью модели "затраты-выпуск" базируется
на предположении о линейности производственных связей, т.е. предполагается, что объем
выпускаемой каждой отраслью продукции прямо пропорционален затратам на ее
производство. Как следствие, производственные связи математически могут быть
представлены в виде системы линейных уравнений.
Для составления линейной модели, соответствующей нашей задаче введем
следующие обозначения:
x 1 — валовой продукт I отрасли (строительство);
x 2 — валовой продукт II отрасли (машиностроение);
x 3 — валовой продукт III отрасли (прочие отрасли).
y 1 — конечный продукт I отрасли (строительство);
y 2 — конечный продукт II отрасли (машиностроение);
y 3 — конечный продукт III отрасли (прочие отрасли),
Сразу оговорим, что все величины, используемые для количественного анализа могут
быть представлены в натуральном (единицах продукции) и в стоимостном (денежных
единицах) виде. На первом этапе решения более уместно и даже необходимо использовать
натуральное представление.
Составив межотраслевую таблицу данного производства, дадим интерпретацию ее
элементов с учетом всего вышесказанного.
Отрасли
Потребители
хозяйства
Производители
Конечный
Валовой
1
2
3
продукт
продукт
1
x 11
x 12
x 13
y1
x1
2
x 21
x 22
x 23
y2
x2
3
x 31
x 32
x 33
y3
x3
где x ij — количество продукции отрасли і, необходимое для производства валового
продукта отрасли j. Необходимо подчеркнуть, что здесь и в дальнейшем индекс i будет
указывать на производящую отрасль, j — на потребляющую.
Строки приведенной таблицы показывают распределение выпуска каждого вида
продукции. Каждая строка характеризуется следующим балансом:
Выпуск данного
вида продукции
=
Промежуточный
спрос
+
Конечный
спрос
Этот баланс математически может быть записан как:
X

X

X



X
Y
i
i
1
i
2
in
i или
n
xi xij yi
j1
(i=1,2, …,n)
или в виде системы линейных уравнений (при n=3)
x
x
x
y
x

11
12
13
1
1

x
x
x
y2x

21
22
23
2

x
x
x
y
x
31
32
33
3
3

Далее удобно перейти к нормированным величинам. Другими словами, к количеству
потребляемой продукции, отнесенному к единице производимой продукции. Действительно,
нетрудно понять, что пока технология производства остается неизменной, так же остается
x ij
неизменным отношение x . Это легко пояснить на примере. Пусть некоторая отрасль 1
j
занимается сборкой автомобилей, закупая комплектующие у других отраслей. У отрасли 2,
производящей автомобильные шины, отрасль 1 должна закупить 4 единицы продукции для
производства единицы своей продукции. Каким бы ни был валовой выпуск 1-й отрасли x 1 ,
отношение количества комплектующих x 1 j (автомобильных шин) к валовому выпуску
x 21
 4.
x i (количеству автомобилей) будет постоянным
x1
Величина, равная данному соотношению, получила название технологического
(производственного) коэффициента.
a ij 
x ij
xj
Тогда производственный баланс отраслей хозяйства можно представить в виде
следующей таблицы:
Отрасли
Потребители
хозяйства
Производители
1
Конечный
Валовой
2
3
продукт
продукт
1
x 11 = a11 x1
a 12 x 2
a 13 x 3
y1
x1
2
a 21 x 1
a 22 x 2
a 23 x 3
y2
x2
3
a 31 x 1
a 32 x 2
a 33 x 3
y3
x3
Баланс производства на основе данной таблицы будет описываться как:
3
aijx
y


x
a
x

a
x

a
x

y

i
i
i
i
i
1
1
i
2
2
i
3
3
iили x
j
1
(i=1,2, 3)
Зависимости, представленные внутри таблицы можно выразить и с помощью системы
линейных уравнений:
a
x
a
x
a
x
y
x

11
1
12
2
13
3
1
1

a
x

a
x

a
x

y

x
211 222 233 1 2,

a
x
a
x
a
x
y
x
31
1
32
2
33
3
1
3

где каждый из производственных коэффициентов a ij показывает, какое количество
продукции отрасли i необходимо для производства единицы валовой продукции отрасли j.
Эта система балансовых линейных уравнений может быть решена матричным
методом, что является более предпочтительным ввиду более удобного способа вычислений и
возможности использования компьютерных электронных таблиц, входящих в состав
стандартного офисного программного обеспечения.
В матричном представлении приведенную систему уравнений можно записать
следующим образом:
x
x
y
a





1
1
1
11a
12a
13








x

a
a

x

y
2
21
22a
23
2
2















a
a
a
x
x
y
3 3
3 31 32 33

X  A XY
или, в более компактной форме:
Установить зависимость валового продукта от изменения величины конечного
продукта, можно, произведя следующие преобразования,
XA XY; IXAXY;
XI AY;
окончательно будем использовать это уравнение в виде:
XIA Y
1
Последнее матричное
x
y
s


1 
1 уравнение известно как
11 s
12 s
13
  
 

x
s
y
2
21 s
22 s
23
2



 уравнение Леонтьева. Введя








s
x
y
31 s
32 s
33
3
3


 
 обозначение S I  A1,
перепишем это уравнение в виде
X  S  Y , т.е.
где каждый элемент s ij есть коэффициент, выражающий потребность в выпуске
валовой продукции отрасли i для производства единицы конечного продукта отрасли j,
т.е. s ij показывает, каким должен быть выпуск валовой продукции отрасли i, чтобы отрасль j
могла произвести единицу конечного продукта при условии сохранения экономического
1
равновесия в данном многоотраслевом хозяйстве. Матрица S I  A называется муль-
типликатором Леонтьева, знание этой матрицы позволяет без труда оценить различные
варианты работы многоотраслевого хозяйства.
Здесь начинается следующий этап анализа, на котором для описания величин,
характеризующих
деятельность
многоотраслевого
хозяйства,
будем
использовать
стоимостное представление.
Составим таблицу межотраслевого баланса трехотраслевого производства и дадим
интерпретацию ее элементов с учетом новых единиц представления. Необходимо отметить,
что при переходе к стоимостным единицам становится целесообразным анализ не только
строк таблицы МБ, характеризующих производительный аспект деятельности отрасли, но и
столбцов таблицы, что позволяет количественно оценить затраты на производство и
определить доход каждой отрасли и всего хозяйства в целом.
Отрасли
Потребители
хозяйства
Конечный
Валовой
1
2
3
спрос
продукт
1
a 11 x 1
a 12 x 2
a 13 x 3
y1
x1
2
a 21 x 1
a 22 x 2
a 23 x 3
y2
x2
3
a 31 x 1
a 32 x 2
a 33 x 3
y3
x3
Чистый
Зарплата
a1x1
a 2x2
a 3x3
доход
Прибыль
d1 x 1
d2x2
d3x 3
x1
x2
x3
Производители
Валовой продукт
х
где x n — стоимость валовой продукции отрасли n;
y n — стоимость конечного продукта отрасли n;
x ij
a ij — коэффициент прямых затрат, определяемый соотношением a ij 
xj ;
x ij — затраты отрасли j на производство валового продукта, определяемые
произведением коэффициента прямых затрат на стоимость валовой продукции xij aij  xj ;
m n — чистый доход производства, определяемый как разность стоимости валового
продукта отрасли и затрат отрасли на ее выпуск
n
d
x
ajn
x

n
n
n
j
1
a n — заработная плата (доля) на единицу стоимости продукции i - той отрасли;
d n — доля прибыли на единицу стоимости продукции i - той отрасли;
x — стоимость всего совокупного продукта многоотраслевого хозяйства в целом.
При использовании стоимостных единиц, смысл элементов матричного
мультипликатора Леонтьева можно определить так:
b ij — коэффициент полных затрат отрасли на производство единицы конечного
1
продукта y i , как следствие, мультипликатор Леонтьева S I  A иногда называют
матрицей полных затрат многоотраслевого хозяйства.