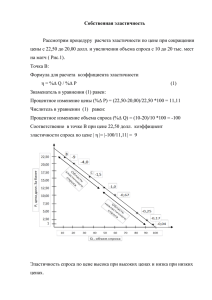
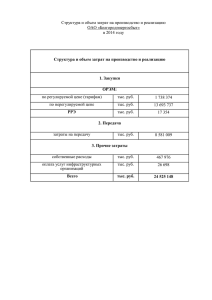
А) Рынок пассивный:
реклама

А) Рынок пассивный: Желаем продать по цене выше рыночной в два раза (не за 1000, а за 2000), извольте ждать не 1 ед. времени, а 1,5 ед. И действительно, эффект «рынка лимонов» для пассивного рынка характерен. Как видно из рисунка, снижение цены ниже рыночной не приводит к ажиотажу, а, наоборот, к постепенному снижению интенсивности спроса. Б) Рынок активный: Желаем продать по цене выше рыночной в два раза (не за 1000, а за 2000), придется ждать долго - не 1 ед. времени, а долго-долго …. Так, что при высокой эластичности спроса по цене после 1РС почти наблюдается тот эффект, о котором Вы, Василий Григорьевич, говорите. Честно говоря, мне здесь не все понятно. Но, я же говорил, что данная модель построена при допущении, что эластичность неизменна вблизи точки (Тр, tp). Думаю, что для решения задач, связанных с обоснованием ликвидационной цены и кредиторской скидки, пока не разберемся путем рыночных подтверждений с зависимостью эластичности от цены, это все вполне пригодно. Принимая во внимание значительные разбросы цен и связанные с этим неопределенности. Ваши, Василий Григорьевич, рассуждения о поведенческих мотивациях формирования ценовой эластичности, конечно же, имеют право на жизнь. Так и надо делать. Но я остаюсь при своем, что вербальные (сужденческие) умозаключения хорошо бы подкреплять данными рынка. И тогда все будет получаться замечательно! А дифференциальное уравнение dn C El (С ) , dC n при переменной в зависимости от цены С эластичности решить не проблема. Была бы ясность с видом и параметрами этой самой El(C). Ну и, наконец, о необходимости учета изменения цен в будущем, о чем говорит Сергей Абрамович. Давайте сначала как-то договоримся или определимся, не знаю прямо, с этой вот простотой. Затем будем думать, как сюда затолкать время, ну и другие факторы, разумеется. От простого к сложному. Не сразу же все объять, которое необъятное. С уважением, В. Михайлец