Задача № 3 симметричную систему ЭДС) и симметричную нагрузку Действующие значения
реклама
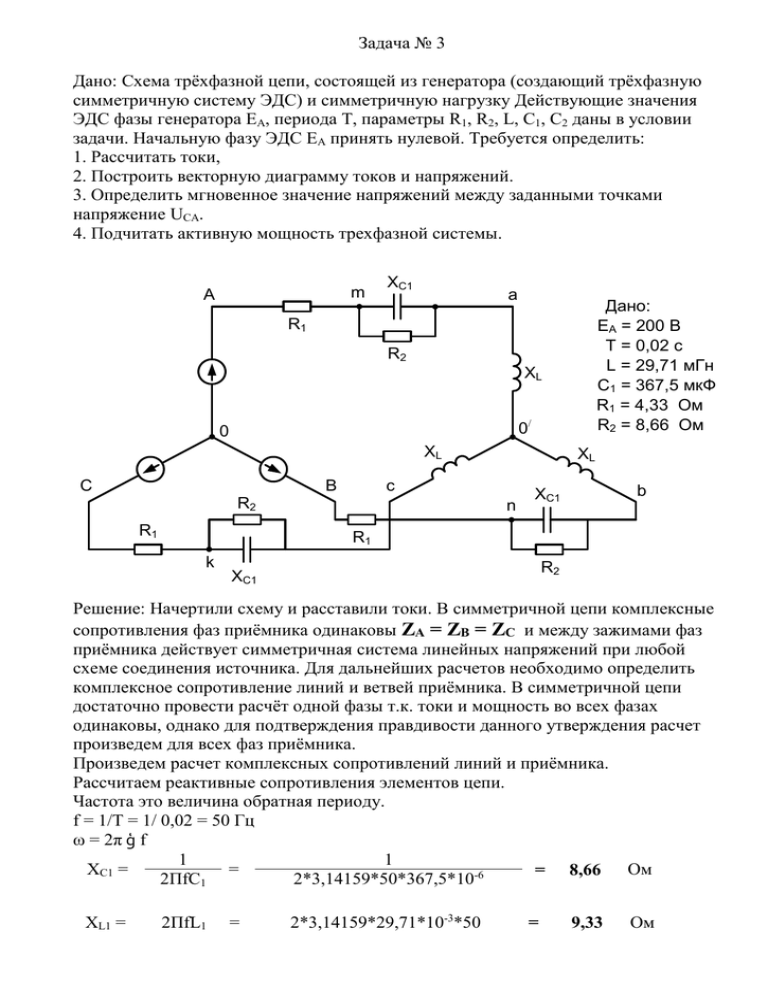
Задача № 3 Дано: Схема трёхфазной цепи, состоящей из генератора (создающий трёхфазную симметричную систему ЭДС) и симметричную нагрузку Действующие значения ЭДС фазы генератора ЕА, периода Т, параметры R1, R2, L, C1, C2 даны в условии задачи. Начальную фазу ЭДС ЕА принять нулевой. Требуется определить: 1. Рассчитать токи, 2. Построить векторную диаграмму токов и напряжений. 3. Определить мгновенное значение напряжений между заданными точками напряжение UCA. 4. Подчитать активную мощность трехфазной системы. m A ХC1 a Дано: ЕА = 200 B Т = 0,02 с L = 29,71 мГн С1 = 367,5 мкФ R1 = 4,33 Oм R2 = 8,66 Oм R1 R2 ХL 0/ 0 ХL C B c R2 R1 ХL n b ХC1 R1 k R2 ХC1 Решение: Начертили схему и расставили токи. В симметричной цепи комплексные сопротивления фаз приёмника одинаковы ZA = ZB = ZC и между зажимами фаз приёмника действует симметричная система линейных напряжений при любой схеме соединения источника. Для дальнейших расчетов необходимо определить комплексное сопротивление линий и ветвей приёмника. В симметричной цепи достаточно провести расчёт одной фазы т.к. токи и мощность во всех фазах одинаковы, однако для подтверждения правдивости данного утверждения расчет произведем для всех фаз приёмника. Произведем расчет комплексных сопротивлений линий и приёмника. Рассчитаем реактивные сопротивления элементов цепи. Частота это величина обратная периоду. f = 1/Т = 1/ 0,02 = 50 Гц ω = 2π ģ f 1 1 ХC1 = = = 8,66 Ом 2ПfC1 2*3,14159*50*367,5*10-6 ХL1 = 2ПfL1 = 2*3,14159*29,71*10-3*50 = 9,33 Ом Выразим комплексное сопротивление линии. Линия состоит из параллельно соединённых сопротивлений активного R2 и реактивного ХС1 и последовательно соединенного активного сопротивления R1 Выразим сопротивления в комплексной форме. ZR2 = 8,66 + j 0 = 8,66 * e j 0 ZXС = 0 – j 8,66 = 8,66 * e –j 90 Параллельно соединенные сопротивления определяем по следующей формуле. ZR2 · ZXС ZПЛа = ZПЛв = ZПЛс = ZR2 + ZXС ZПЛа = 8,66 * e j 0 * 8,66,0 * e –j 90 8,66 + j 0 + 0 – j 8,66 = 75 * e –j 90 8,66 – j 8,66 = 75 * e –j 90 12,24 * e –j 45 = 6,1239 * e –j 45 = 4,33 – j 4,33 Комплексное сопротивление линии определяется по следующей формуле. ZЛа = ZЛb = ZЛс = ZПЛа + ZR1 = 4,33 – j 4,33 + 4,33 + j0 = 8,66 – j 4,33 = 9,682 * e –j 26,57 Комплексное сопротивление линии имеет реактивное (ёмкостное) сопротивление. Приёмник имеет реактивное (индуктивное) сопротивление. Выразим данное сопротивление в комплексной форме ZПра = ZПрb = ZПрс = 0 + j 9,33 = 9,33 * e j 90 Рассмотрим одну фазу: источник – линия – приёмник. Два последовательных сопротивления ZЛа и ZПра преобразуем в одно сопротивление. Zа = Zb = Zс = ZЛа + ZПра = 8,66 – j 4,33 + 0 + j 9,33 = 8,66 + j 5 = 10,0 * e j 30 Так как по условию задачи нам задано действующее значение ЭДС фазы, а это означает что нам дано фазное значение фазы А Действующее значение ЭДС меньше в √2 раз его амплитудного значения. еа = √2 * Еa = √2 * 200 = 282,84 В Так как начальная фаза ЭДС ЕА равна нулю (по условию задачи) то можно записать еа = 282,84 sin (ωt – 0) Так как в трехфазной цепи протекает симметричный ток, где смещение каждой фазы друг от друга составляет 120 0, смещение фазы В от фазы А равно – 120 0, а смещение фазы С от фазы А равно – 240 0 (или на + 120 0) Для других фаз можно записать еb = 282,84 sin (ωt – 120) ес = 282,84 sin (ωt – 240) = 282,84 sin (ωt + 120) Запишем значение ЭДС фаз в комплексной форме Ėа = 282,84 * e j 0 = 282,84 + j 0 Ėb = 282,84 * e – j 120 = – 141,42 – j 244,95 Ėс = 282,84 * e j 120 = – 141,42 + j 244,95 Произведём расчет комплексного значения тока для фаз А, В и С İa = Ėа /Za = 282,84 * e j 0 /10,0 * e j 30 = 28,284 * e – j 30 = 24,49 – j 14,142 İb = Ėb /Zb = 282,84 * e – j 120/10,0 * e j 30 = 28,284 * e – j 150 = – 24,49 – j 14,142 İc = Ėс /Zc = 282,84 * e j 120/10,0 * e j 30 = 28,284 * e j 90 = 0 + j 28,284 При соединении приёмника в «звезду» фазное значение тока равно линейному. Равенство нулю суммы линейных токов является общим свойством трёхфазных трехпроводных цепей при соединении «звездой» и «треугольником» при симметричной и несимметричной нагрузке. İa + İb + İc = (24,49 – j 14,142) + (– 24,49 – j 14,142) + (0 + j 28,284) = 24,49 – 24,49 + j 28,284 – j 28,284 = 0 Произведем вычисления падения напряжения на последовательных сопротивлениях ZЛа и ZПра. Для фазы А Ů ZЛа = İa * ZЛа = 28,284 * e – j 30 * 9,682 * e –j 26,57 = 273,85 * e –j 56,57 = 150,87 – j 228,54 Ů ZПра = İa * ZПра = 28,284 * e – j 30 * 9,33 * e j 90 = 263,89 * е j 60 = 131,94 + j 228,54 Сумма падений напряжений на последовательных сопротивлениях равно ЭДС источника для одной фазы. Ėа = Ů ZЛа + Ů ZПра = 150,87 – j 228,54 + 131,94 + j 228,54 = 282,81 + j 0,0 ≈ 282,84 + j 0,0 = 282,84 * e j 0 Произведем расчет для остальных фаз Для фазы В Ů ZЛb = İb * ZЛb = 28,284 * e – j 150 * 9,682 * e –j 26,57 = 273,85 * e – j 176,57 = –273,36 – j 16,384 Ů ZПрb = İb * ZПрb = 28,284 * e – j 150 * 9,33 * e j 90 = 263,89 * е – j 60= 131,94 – j 228,54 Ėb = Ů ZЛb + Ů ZПрb = –273,36 – j 16,384 + 131,94 – j 228,54 = – 141,42 – j 244,92 ≈ 141,42 – j 244,95 = 282,84 * e – j 120 Для фазы С Ů ZЛс = İс * ZЛс = 28,284 * e j 90 * 9,682 * e –j 26,57 = 273,85 * e j 63,46 = 122,36 + j 244,99 Ů ZПрс = İс * ZПрс = 28,284 * e j 90 * 9,33 * e j 90 = 263,89 * е j 180 = – 263,89 + j 0 Ėс = Ů ZЛс + Ů ZПрс = 122,36 + j 244,99 – 263,89 + j 0 = 141,53 + j 244,99 ≈ 141,42 + j 244,95 282,84 * e j 120 3. Определим мгновенное значение напряжений между точками с и а приемника. Так как точки с и а находятся на концах приемника, а это означает, что необходимо найти линейное напряжение приемника между фазами а и с. Ůса = Ů ZПрс – Ů ZПра = (– 263,89 + j 0) – (131,94 + j 228,54) = – 395,83 – j 244,54 = 465,27 * е – j 148,29 еса = 465,27 sin (ωt – j 148,29) Активная мощность системы определяется произведением комплекса напряжения на сопряженный комплекс тока. Произведем расчет для каждой фазы системы отдельно. Запишем значения сопряженного комплекса тока для каждой фазы. (İa) = 24,49 + j 14,142 = 28,284 * e j 30 (İb) = – 24,49 + j 14,142 = 28,284 * e j 150 (İc) = 0 – j 28,284 = 28,284 * e – j 90 ŠА = UА (İА) = РА + j QA = (282,84 * e j 0)*( 28,284 * e j 30) = 7999,85 * e j 30= 6928,075 + j 3999,92 ВА ŠВ = UВ (İВ) = РВ + j QВ = (282,84 * e – j 120)*( 28,284 * e j 150) = 7999,85 * e j 30 = 6928,075 + j 3999,92 ВА ŠС = UС (İС) = РС + j QС = (282,84 * e j 120)*( 28,284 * e – j 90) = 7999,85 * e j 30 = 6928,075 + j 3999,92 ВА Активная мощность системы составляет Р = РА + РВ + РС = 6928,075 + 6928,075 + 6928,075 = 20784,225 Вт Реактивная мощность системы составляет Q = QА + QВ + QС = 3999,92 + 3999,92 + 3999,92 = 11999,77 ВАр Знак плюс указывает на индуктивный характер реактивной мощности цепи. Полная мощность трехфазной системы составляет ŠП = ŠА + ŠВ + ŠС = 6928,075 + j 3999,92 + 6928,075 + j 3999,92 + 6928,075 + j 3999,92 = 20784,225 + j 11999,77 = 23999,55 * e j 30 Векторная диаграмма Ic С ŮZЛc Ėс Ů ZПра Ů ZПрс А Ėа O ŮZЛb Ib Iа Ėb ŮZЛа Ů ZПрb Масштаб В По напряжению в 1 мм 3 В По току в 1 мм 0,333 А