ПРОЦЕССЫ ГОРЕНИЯ И ВЗРЫВА

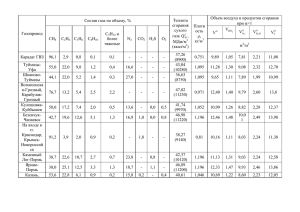
РАСЧЁТ ТЕПЛО– И МАССООБМЕНА В НИЗКОТЕМПЕРАТУРНОМ
ГАЗОГЕНЕРАТОРЕ КАССЕТНОГО ТИПА
ПРОЦЕССЫ ГОРЕНИЯ И ВЗРЫВА
УДК 519.6:536.24
РАСЧЁТ ТЕПЛО– И МАССООБМЕНА В НИЗКОТЕМПЕРАТУРНОМ
ГАЗОГЕНЕРАТОРЕ КАССЕТНОГО ТИПА
КИРИЛЛОВ В.В.
Южно-Уральский государственный университет, 454080, г.Челябинск,
проспект им. В.И. Ленина, 76
________________________________________________________________________________
АННОТАЦИЯ. В работе предложена математическая модель процессов тепло- и массообмена в
низкотемпературном твёрдотопливном газогенераторе с камерой охлаждения (НТГГ) кассетного типа.
Разработан численный метод решения уравнений математической модели на базе неявной разностной схемы.
________________________________________________________________________________________________
КЛЮЧЕВЫЕ СЛОВА: твёрдое топливо, камера охлаждения, охладитель, тепломассообмен, математическая
модель, разностная схема, численный метод.
Схема НТГГ кассетного типа представлена на рис. 1. Работа НТГГ осуществляется
следующим образом. Пиропатрон запуска 1 зажигает воспламенитель 2, воспламеняющий в
свою очередь заряд 4 в камере сгорания 3. Продукты сгорания через сопловые отверстия
газохода 5 поступают в кассеты с охладителем 7, где и протекает процесс разложения
последнего. Охлаждённый газ поступает в кольцевой канал 8 камеры охлаждения 6.
Из камеры 6 газ через фильтр, коллектор и выходной штуцер поступает к потребителю.
1––пиропатрон; 2– воспламенитель; 3–камера сгорания; 4–твёрдое топливо; 5–газоход;
6–камера охлаждения; 7–кассета с охладителем; 8–кольцевой канал
Рис. 1. Схема НТГГ с камерой охлаждения кассетного типа
1. Математическая модель НТГГ
Математическая модель камеры сгорания (КС) включает в себя уравнения рабочих
процессов в воспламенителе, переднем объёме, канальной части с шашками топлива и в
выходном объёме. Рабочие процессы в воспламенителе, переднем и выходном объёмах
камеры сгорания описываются в рамках термодинамических математических моделей,
включающих в себя уравнения баланса массы, энергии смеси газов, уравнения баланса массы
компонентов газовой смеси, уравнения теплопроводности стенок [1]. Газовую смесь в КС
можно разделить на неконденсирующиеся (НК) продукты сгорания топлива (ПСТ) и
воспламенителя (ПСВ), такие, как углекислый газ, окись углерода и т.п., воздух и водяной
пар. Предполагается, что все компоненты газовой смеси с достаточной точностью
подчиняются уравнению состояния идеального газа.
ХИМИЧЕСКАЯ ФИЗИКА И МЕЗОСКОПИЯ. 2011. Том 13, №1
5
КИРИЛЛОВ В.В.
Заряд топлива в КС состоит из цилиндрических канальных шашек, горящих по боковой
поверхности. Процессы течения продуктов сгорания в канальной части описываются
системой одномерных уравнений неразрывности, количества движения и энергии газовой
смеси, а также одномерными уравнениями баланса массы компонентов смеси.
Температурное поле в шашке топлива рассчитывается из одномерного уравнения
теплопроводности для области с движущимися границами. Распределение температуры в
стенке определяется из решения одномерного уравнения теплопроводности.
 кс S кс Gкс

 uтт П т ;
(1)

x
2

Gкс   Gкс
G2 П
 
 pкс S кс    кс кс2 экв ;
(2)

x   кс S кс
8
S

кс кс


кс S кс eкс    Gкс eкс  pкс S кс wкс    т u т hт П т  Qкс ;

x
w2
Qкс   кс Tкс  Tw, кс П w ,кс ;
eкс  cvксTкс  кс ;
2
 кс S кс g кс,п Gкс g кс,п

 u т  т П т  п,т ;

x
кс S кс g кс,в Gкс g кс,в

0;

x
кс S кс g кс,т Gкс g кс,т

 u т  т П т 1  п,т  ;

x
pкс  кс RксTкс ;
Tw, м
(3)
(4)
(5)
(6)
(7)
aм   Tw, м 
r
;
(8)

r r  r 
RTт r a т  2Tт r 1  2 y u тTт r  a тTт 


 qv rR ;
(9)

R y 2
y
r  R1  
y
;
R  R2   R1  .
R
В (1) – (9)  – плотность; G – расход; p – давление; Т – температура; S – площадь
свободного сечения; w – скорость; h – энтальпия; u – скорость горения; П – периметр; Q –
тепловой поток; g – массовая доля;  п,т – массовая доля водяного пара в продуктах сгорания
топлива; R – газовая постоянная;  – коэффициент теплоотдачи; сv – удельная теплоёмкость
при постоянном объёме; а – коэффициент температуропроводности; R1 , R2 – внутренний и
наружный радиусы шашки топлива;  – коэффициент гидравлического сопротивления;  –
время; х – продольная координата; r – радиальная координата; индексы: кс – камера
сгорания; т – топливо; п – водяной пар; в – воспламенитель; w – стенка; м – металл.
Процессы тепло– и массообмена в кассетах с охладителем описываются одномерными
уравнениями, полученными путём осреднения по ширине кассеты двумерных уравнений
движения вязкого теплопроводного газа в цилиндрических координатах. Охладитель в
кассетах находится в виде цилиндрических гранул, полученных прессованием из порошка.
Система уравнений имеет следующий вид.
i S i ' Gi
(10)

 П экв j m  П экв jc ;

r
Gi2 П эфф
Gi Gi vi
pi Si ' Si ' pi



 i
 Si 'vi jm  Si 'vi jc ;
(11)
'2

r
r
r
8S i  i
6

ХИМИЧЕСКАЯ ФИЗИКА И МЕЗОСКОПИЯ. 2011. Том 13, №1
РАСЧЁТ ТЕПЛО– И МАССООБМЕНА В НИЗКОТЕМПЕРАТУРНОМ
ГАЗОГЕНЕРАТОРЕ КАССЕТНОГО ТИПА


Q
i ei Si ' 

Gi ei  pi Si' vi   w,i  П экв jm hs  П экв jc rs ;

r
l
i Si ' g i ,п

i S i ' g i ,т

i Si ' g i ,х

dTw ,i
d




Gi g i ,п
r
Gi g i ,т
r
Gi g i ,х
(12)
 S i ' j m  х  S i ' jc ;
(13)
 0;
(14)
 Si ' jm 1   х  ;
(15)
r
 i 1 Ti-1  Tw ,i Fw, i
cм  мVw

 i Ti  Tw ,i Fw, i
cм  мVw
;.
(16)
S '  2rl .
В уравнениях (10) – (16) i – номер кассеты;  – пористость слоя гранул;  x – массовая
доля водяного пара в продуктах разложения охладителя; j m – плотность потока массы
продуктов разложения охладителя; j c – плотность потока массы конденсации водяного
пара; rs – теплота парообразования; l – ширина кассеты; П эфф –эффективный
гидравлический периметр кассеты; V – объём; индексы: х – охладитель.
Неконденсирующиеся газы в смеси подчиняются уравнению состояния идеального
газа. В процессе охлаждения продуктов сгорания водяной пар может конденсироваться как в
объёме потока, так и на стенках кассеты. В связи с этим водяной пар может находиться
близко к линии насыщения, поэтому его состояние не соответствует уравнению состояния
идеального газа и должно определяться по уравнениям [2].
Движение газовой смеси в газоходе и кольцевом канале описывается одномерными
уравнениями неразрывности, количества движения и энергии газовой смеси, а также
одномерными уравнениями баланса массы компонентов смеси в следующем виде.
Ф 

F;
(17)

x
0


G
 S 


2



w
П
(18)
Ф   G  ;    Gw  pS  ; F   
.
8 

eS 
Ge  pwS 
  П w q w 
Sg j Gg j

 0 , j=в, т, п, х.
(19)

x
Температурное поле в стенке описывается уравнение теплопроводности вида (8)
с граничными условиями третьего рода.
Начальные условия системы уравнений определяют значения температуры, расхода и
давления в начальный момент времени. Температура всех элементов одинакова и равна
некоторой начальной температуре T0 . Давление во всех точках НТГГ равно начальному p0 ,
расход равен нулю. Массовые доли продуктов сгорания воспламенителя, топлива и
продуктов разложения охладителя равны нулю.
Рассмотрим постановку граничных условий. На входе в канальную часть КС
2
,0
k кс1
k
pкс ,0   кс wкс
Rкс1Tкс1   кс

;
(20)
k кс1  1
k кс  1  кс1 
2
2
,0 ;
pкс1   pкс ,0  кс ,0wкс
g кс ,п ,0   g кс1,п  ;
g кс ,в ,0  g кс1,в  .
ХИМИЧЕСКАЯ ФИЗИКА И МЕЗОСКОПИЯ. 2011. Том 13, №1
(21)
(22)
7
КИРИЛЛОВ В.В.
В (20) – (22) k  c p cv ; индекс кс1 обозначает параметры переднего объёма КС.
На входе в газоход
pкс 2   pг ,0  pвх ;
Gкс 2  Gг ,0 ;
hкс 2   hг ,0 ;
g кс2,п   g г,п ,0 ;
g г,н ,0   g кс2,в   g кс2,т   .
(23)
В (23) индекс кс2 обозначает параметры выходного объёма КС.
На входе в кассеты из газохода поток газа разветвляется. Часть газа входит в кассету,
часть газа проходит дальше в газоход. Схема потоков представлена на рис. 2. В соответствии
со схемой
1
1
i
1
1
Рис. 2. Расчётная схема потоков в газоходе
Gг ,i 1  Gг ,i  Gi ;
g гн,i 1  g гн,i ;
hг ,i 1  hг ,i ;
pг ,i 1  pг ,i  pi
g гп,i 1  g гп,i .
(24)
(25)
Здесь Gi – расход газа в i–ю кассету; Gг ,i , Gг ,i 1 – расходы газа в газоходе до и после
точки разветвления;
hг ,i 1 , hг ,i
– энтальпия газа до и после точки разветвления;
g гп, i 1 , g гп,i , g гн,i 1 , g гн,i – массовые доли водяного пара и НК газов в газоходе до и после
точки разветвления; p г ,i , pг ,i 1 , pi – давление газа до и после точки разветвления, а также
потери давления при переходе через точку разветвления. Индекс г означает параметры
газохода. На входе в i–ю кассету
2
kг 1 

kг

k
k

k




г
г
p 0 
2k г
 p 0 
 pi 0   2  г 1
 г,i pг,i  i    i 
 i S отв
 , p   k  1 
 p 
 p 
kг  1

г,
i
г,
i
г,i
 г







Gi  
;
(26)


1
kг

 2  kг 1 2k г

p 0   2  kг 1


 г,i pг,i , i
 
  i S отв 
k

1
k

1
p
k

1
г
г
г,
i
г





hi 0  hг ,i ;
g i ,п , Rвн   g гп,i ;
(27)
g i ,т , Rвн   g гн,i ;
g i ,х , Rвн   0 .
(28)
Здесь Rвн – внутренний радиус кассеты. На выходе из кассеты
ki
2
ki 1 


k
 вых
2k i
 pк  ki   pк  ki  , pк   2  i 1

S

p
 i
отв
i i 
 p   p  k 1
ki  1
p 
i
 i 



вых
 i 
.
(29)
Gi  

1
k
i

 2  ki 1 2ki
pк  2  ki 1
 вых

i pi ,
 
  i S отв  k  1 
k

1
p
k

1
i
i
 i 
 i 

Здесь pi , pк – давление на выходе из i-й кассеты и давление в кольцевом канале
в точке слияния, соответственно; ki , i – отношение теплоёмкостей и плотность на выходе из
i-й кассеты.
8
ХИМИЧЕСКАЯ ФИЗИКА И МЕЗОСКОПИЯ. 2011. Том 13, №1
РАСЧЁТ ТЕПЛО– И МАССООБМЕНА В НИЗКОТЕМПЕРАТУРНОМ
ГАЗОГЕНЕРАТОРЕ КАССЕТНОГО ТИПА
В кольцевом канале потоки газа из кассет смешиваются с газом в канале. Схема
потоков газа изображена на рис. 3. В соответствии со схемой
1
1
1
Рис. 3. Схема потоков в кольцевом канале
Gк ,i 1  Gк ,i  Gi ;
hк ,i 1Gк ,i 1  hк ,i Gк ,i  hi Gi ;
pк ,i 1  pк ,i  pi ;
g кj,i 1Gк ,i 1  g кj,i Gк ,i  g j,i Gi , j=т,п,х.
(30)
(31)
Здесь hi , Gi , g т ,i , g х ,i , g п,i – энтальпия, расход, массовые доли НК газов ПСТ и ПСВ,
НК газов продуктов разложения охладителя, водяного пара на выходе из i–й кассеты. Индекс
к означает параметры кольцевого канала.
Расход из кольцевого канала к потребителю определяется по формулам
2
k 1 

k

k
k





k
p
p
p
2k
 2  1
 к pк  0    0   , 0  

 вых S вых
k 1
pк   pк 
pк  k  1 




Gвых  
.
(32)
1
k

p

 2  k 1 2k
 2  k 1
 к pк , 0  

  вых S вых  k  1 
k 1
pк  k  1 

Здесь к , pк – плотность и давление на выходе из кольцевого канала, p0 – давление
у потребителя.
2. Численный метод решения уравнений математической модели
Система уравнений состоит из обыкновенных дифференциальных уравнений и
уравнений в частных производных. Для численного интегрирования обыкновенных
дифференциальных уравнений применялся метод Рунге-Кутта 4-го порядка. Для решения
уравнений в частных производных применялся метод конечных разностей. Решение краевой
задачи выполнялось методом ортогональной прогонки [3]. В КС, газоходе, кассетах и
кольцевом канале строились равномерные разностные сетки.
Уравнения неразрывности, количества движения и энергии аппроксимируются
неявными разностными схемами и приводятся к векторным уравнениям вида [4]
AnYnm1  Bn1Ynm11  Cn .
(33)
Граничные условия на входе в КС преобразуются к виду
A1Y1m1  C1 .
(34)
В КС и газоходе дифференциальные уравнения аппроксимировались на разностной
сетке, конструкция которой представлена на рис. 4.
1
Рис. 4. Разностная сетка в КС и газоходе
ХИМИЧЕСКАЯ ФИЗИКА И МЕЗОСКОПИЯ. 2011. Том 13, №1
9
КИРИЛЛОВ В.В.
Узел M – последний узел КС, узел M  1 – первый узел газохода. Газоход разделён на
отрезки, количество которых равно числу кассет +один, каждый из которых содержит по
несколько узлов. Первые три условия перехода от КС к газоходу (23) в разностной
аппроксимации имеют следующий вид.
YMm1  YMm11   ,
(35)
где  – квадратная матрица 3 3 , а  – вектор размерности 3. Условия перехода в газоходе
(24) в разностной аппроксимации также могут быть представлены в виде
YNmi 1   iYNmi 11   i .
(36)
В конце газохода граничное условие записывается в виде
(37)
GN  0 .
Краевая задача для КС и газохода решается методом ортогональной прогонки. Расчёт
выполняется последовательными приближениями до тех пор, пока во всех узлах разностной
сетки значение относительной погрешности по давлению, расходу и температуре не станут
меньше заданных. Обычно величина погрешности задавалась порядка 0,1 %. После решения
краевой задачи решаются уравнения баланса массы компонентов газовой смеси по
разностным уравнениям вида
b g m1  cn
g nm1  n1 n1
,
(38)
an
в которых
(39)
a n  S mn1 h  Gnm1 ;
cn  Sg mn h  hJ nm1 .
bn1  Gnm11 ;
Здесь h,  – шаги разностной схемы по пространственной координате и времени,
соответственно. После этого определяются значения расходов на входе в кассеты
с охладителем по формулам (26).
Уравнения (10) – (12) аппроксимируются аналогично уравнениям КС и газохода и
приводятся к виду (33). Граничные условия (26), (27) преобразуются к виду (34), условие (29)
преобразуется к виду [4]
(40)
BN YNm1  C N .
где BN – матрица 1 3 , C N – скаляр. Решение уравнений кассет выполняется
последовательными приближениями, аналогично решению задачи для КС и газохода, после
чего решаются уравнения баланса массы компонентов газовой смеси. Затем рассчитываются
расходы на выходе из кассет по формулам (29).
После расчёта кассет с охладителем решаются уравнения математической модели кольцевого канала. Конструкция разностной сетки для кольцевого канала представлена на рис. 5.
G
N i+1 N i
1
N
Gi
Рис. 5. Разностная сетка в кольцевом канале
В узлах стыковки кольцевого канала с кассетами граничные условия (30) в разностной
аппроксимации преобразуются к виду (34), а условия (31) записываются следующим
образом.
g кjm,N1i Gкm,N1i  g mj,i1Gim1
m1
g кj, Ni 1 
, j = т,п,х.
(41)
Gкm, N1i 1
10
ХИМИЧЕСКАЯ ФИЗИКА И МЕЗОСКОПИЯ. 2011. Том 13, №1
РАСЧЁТ ТЕПЛО– И МАССООБМЕНА В НИЗКОТЕМПЕРАТУРНОМ
ГАЗОГЕНЕРАТОРЕ КАССЕТНОГО ТИПА
Граничное условие на выходе из кольцевого канала (32) приводится к виду (40).
Краевая задача решается ортогональной прогонкой.
На рис. 6 показано изменение температуры на выходе из НТГГ. В качестве охладителя
применялся углекислый аммоний. Подъём температуры в начальный период работы вызван
горением воспламенителя. Далее расчётное изменение температуры хорошо согласуется с
результатами эксперимента [4]. На рис. 7 показано изменение расхода газа по длине КС и
газохода в различные моменты времени. На рис. 8 показано изменение температуры по
радиусу кассеты в момент времени 0,1 с. К этому моменту распределение температуры во
всех кассетах практически одинаково.
Рис. 6. Изменение температуры на выходе из НТГГ
Рис. 7. Изменение расхода по длине КС и газохода
Рис. 8. Изменение температуры по радиусу кассеты, =0,1 c
ХИМИЧЕСКАЯ ФИЗИКА И МЕЗОСКОПИЯ. 2011. Том 13, №1
11
КИРИЛЛОВ В.В.
На рис. 9 показано изменение расхода по длине кольцевого канала в различные
моменты времени. К моменту времени 2 с устанавливается практически стационарный
режим течения.
Рис. 9. Изменение расхода по длине кольцевого канала
Расчёты выполнялись с шагом по времени, соответствующим числу Куранта,
определённым как w  c  h =20…25, где h – минимальное значение шага сетки по
пространственной координате; w и с – максимальные значения скорости потока и звука в
НТГГ, соответственно.
СПИСОК ЛИТЕРАТУРЫ
1. Липанов А.М., Бобрышев В.П., Алиев А.В. и др. Численный эксперимент в теории РДТТ. Екатеринбург :
Наука, 1994. 303 с.
2. Вукалович М.П., Ривкин С.Л., Александров А.А. Таблицы теплофизических свойств воды и водяного пара.
М. : Издательство стандартов, 1969. 408 с.
3. Кириллов В.В. Расчётно-теоретическое исследование процессов тепло- и массообмена в низкотемпературных газогенераторах // Химическая физика и мезоскопия. 2008. Т.10, №4. С.428-435.
4. Ваулин С.Д., Калинкин А.М., Ковин С.Г. Низкотемпературные газогенераторы на твёрдом топливе / под
общ. ред. А.М. Липанова. Ижевск : Изд-во ИПМ УрО РАН, 2006. 236 с.
________________________________________________________________________________________________
CALCULATION OF HEAT AND MASS TRANSFER IN THE LOW TEMPERATURE GAS GENERATOR
CARTRIDGE TYPE
Kirillov V.V.
South Ural State University, Chelyabinsk, Russia
SUMMARY. The paper proposed a mathematical model of heat and mass transfer in low-temperature solid-propellant
gas generator with a cooling chamber cartridge type. A numerical method for solving equations of mathematical models
based on an implicit difference scheme.
KEYWORDS: solid fuel, cooling chamber, cooling, heat and mass transfer, mathematical model, the difference
scheme, numerical method.
________________________________________________________________________________________________
Кириллов Валерий Владимирович, кандидат технических наук, доцент кафедры промышленной теплоэнергетики ЮУрГУ,
тел. (351)237-46-66, 8-9127741611, e-mail: [email protected]
12
ХИМИЧЕСКАЯ ФИЗИКА И МЕЗОСКОПИЯ. 2011. Том 13, №1