Лабораторная работа№5
реклама

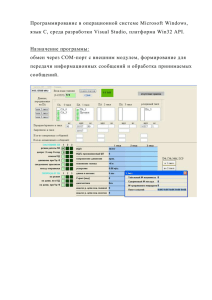
Лабораторная работа сообщений с памятью №5. Энтропия источника дискретных При передаче символов в сообщении вероятность последующего символа связанна с предыдущим символом и определяется смыслом передаваемого сообщения. В связи с этими учет взаимосвязи в последующих символах приводит к уменьшению энтропии. Неопределенность условного распределения символов H ( A / A) не может превышать энтропии их безусловного распределения H ( A) . H ( A / A) H ( A) Обозначим как P(ai / aj ) вероятность того, что источник послал символ a i поле отправки символа a j . Если символ a j принимает произвольное значение из алфавита источника дискретных сообщений, то энтропию источника можно записать как: k H ( A / A) P(aj ) H ( A / aj ) j 1 k k P(aj ) P(ai / aj ) log( P(ai / aj )) i 1 j 1 Типичный пример дискретного источника с памятью – текст, написанный на русском языке. Так, например вероятность появления буквы ‘О’ составляет 0.09, пробел встречается еще чаще, вероятность с которой он встречается в тексте составляет 0.125, в тоже время есть символы которые встречаются намного реже, так например символ ‘Ф’ встречается с вероятностью 0.002. По экспериментальным данным H ( A) 1.5 . Максимальное значение энтропии для языка с алфавитом в 32 символа составляет: дв.ед. . H ( A) max log 2 32 5 символ Таким образом, в обычном тексте содержится в 5 / 1.5 3.3 раза меньше информации, чем в хаотически набранном тексте. Избыточность текста составит: pи 1 H ( A) / H ( A) max 0.7 . Выполнение лабораторной работы Этап I Исследовать работу дискретного канала связи в программе лабораторной работы TIPSlab4.exe. Для выполнения лабораторной работы в программе необходимо перейти в пункт меню «Файл» и установить режим вывода дополнительной информации. Рис. 5.1. Иллюстрация включения режима вывода дополнительной информации После данной операции, программа будет выводить в окне ансамбля дополнительную информацию – H ( A / A) . После этого выполнение лабораторной работы аналогично выполнению предыдущей работы. Введенное сообщение преобразуется в двоичный код, после чего производится анализ ансамбля сообщений источника сообщений и кодера (приемника и декодера). Этап II Написать программу в MatLab для расчета энтропии источника дискретных сообщений с памятью. Программа реализуется на основе программы предыдущей лабораторной работы. Алгоритм программы приведен на рис. 5.2. Иллюстрация работы алгоритма показан на рис. 5.3. i= 1 H2 = 0 S i= 1 i < 256 Ëàá.ðàáîòà ¹ 4 H, Hmax, Pi sum = 0 i < 256 j= 1 j= 1 j < 256 j < 256 sum= sum + P 2(i,j) P2(i, j) > 0 P2=zero(256,256) i= 2 i <= L P2( S(i-1),S(i) ) + 1 j= j+ 1 H2= H2+P(i)* P2(i,j)*lo g2(P(i,j)) i= i+ 1 j= 1 j= j+ 1 j < 256 i= i+ 1 P2(i, j)= P (i, j)/sum j= j+ 1 Pi2=1 - H2/Hmax H2, Pi2 i= i+ 1 Рис. 5.2. Алгоритм программы вычисления информационных характеристик дискретного источника с памятью 2 A A i B A C L A B A C A Âòðîé ñèìâîë Ïåðâûé ñèìâîë A B C sum A 1 2 2 5 B 2 2 C 2 2 Рис. 5.3. Иллюстрация работы программы вычисления энтропии источника дискретных сообщений с памятью Этап III. Изучение информационных характеристик источника дискретных сообщений с памятью более чем на два элемента. Запустить программу TIPSlab5.exe. Изучить информационные характеристики дискретного источника сообщений с памятью на несколько элементов (предельное число выбирается в настройках программы), сравнить с заранее рассчитанными, для русского текста значениями энтропии с памятью на 2, 3, 4 и 5 элементов. В качестве источника сообщений Вам предлагается взять уже готовый текстовый файл, который будет преобразован к одному регистру, и в котором будут оставлены только русские символы. Экспериментально определить значение энтропии с памятью для русского текста. С этой целью компьютер загадает предложение, которое Вам изначально будет неизвестно. Вам необходимо посимвольно угадать все слова этого предложения. Если Вы не правильно угадали символ, то компьютер показывает правильный символ и пишет его в заглавном регистре. После того как будет открыто все предложение, программа по количеству правильно угаданных Вами символов рассчитает избыточность Pи сообщения и энтропию H ( A / A) русского языка полученную по экспериментальным данным. Сравнить значение со значениями полученными в первом этапе лабораторной работы, и с известными Вам из теории. Изучить влияние совместной вероятности появления символов в сообщении. Для этого Вам необходимо ввести сообщение, набор символов которого будет рассматриваться в качестве исходного набора символов для автоматической генерации сообщений. Программа позволяет ввести сообщение, показывает статистику входящих в него символов. После Вам предоставляется возможность сгенерировать сообщение из созданного набора символов на основе вероятности появления символов в русском языке, в том числе и с учетом влияния последовательности появления символов (взаимная вероятность на 2, 3, 4 и 5 символов). Пример и результаты работы программы приведены на рис. 5.4. Рис. 5.4. Изучение статистических свойств русского языка Содержание отчета Отчет по лабораторной работе должен содержать: 1. Пример сообщения и расчет энтропии, избыточности для дискретного источника сообщений с памятью. 2. Алгоритм и листинг программы расчета энтропии, избыточности для источника дискретных сообщений с памятью. 3. Результаты сравнения информационных характеристик источника дискретных сообщений с памятью и без памяти, полученных в собственной реализации и в программе лабораторной работы. 4. Таблицу значений энтропии источника дискретных сообщений с памятью на 2, 3, 4 и 5 символов. Сравнение полученной величины со справочными материалами приведенными в программе. 5. Результаты экспериментального определения энтропии русского языка, включая иллюстрацию способа получения. 6. Результаты автоматического построения предложения из заданного набора символов. Выводы по работе.