ВОПРОСЫ К ВСТУПИТЕЛЬНЫМ ИСПЫТАНИЯМ ПО

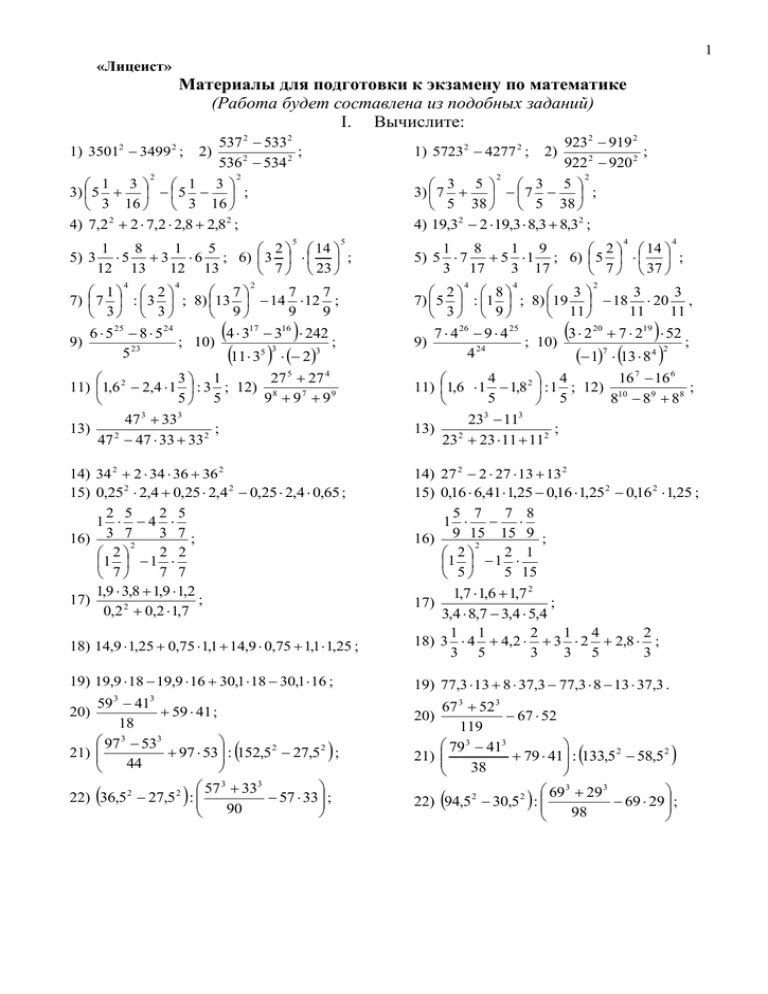
1
«Лицеист»
Материалы для подготовки к экзамену по математике
(Работа будет составлена из подобных заданий)
I. Вычислите:
537 2  5332
1) 3501  3499 ; 2)
;
536 2  534 2
2
2
 1 3  1 3
3)  5     5   ;
 3 16   3 16 
4) 7,2 2  2  7,2  2,8  2,8 2 ;
2
9232  919 2
1) 5723  4277 ; 2)
;
922 2  920 2
2
2
 3 5   3 5 
3)  7     7   ;
 5 38   5 38 
4) 19,32  2  19,3  8,3  8,32 ;
2
2
5
5
1
8
1
5
 2   14 
5) 3  5  3  6 ; 6)  3     ;
12 13
12 13
 7   23 
4
4
2
2
4
4
1
8
1 9
 2   14 
5) 5  7  5  1 ; 6)  5     ;
3 17
3 17
 7   37 
4
4
2
7
7
 1  2
 7
7)  7  :  3  ; 8) 13   14  12 ;
9
9
 3  3
 9
4  317  316  242
6  5 25  8  5 24
9)
;
10)
;
3
3
5 23
11  35   2
3
3
 2  8
 3
7)  5  : 1  ; 8) 19   18  20 ,
11
11
 3  9
 11 
3  2 20  7  219  52
7  4 26  9  4 25
9)
;
10)
;
4 24
 17  13  8 4 2
27  27
3 1

11) 1,6 2  2,4  1  : 3 ; 12) 8
5 5
9  97  99

47 3  333
13)
;
47 2  47  33  332
16 7  16 6
4

 4
11) 1,6  1  1,8 2  : 1 ; 12) 10
;
5
8  8 9  88

 5
233  113
13)
;
23 2  23  11  112
14) 34 2  2  34  36  36 2
15) 0,25 2  2,4  0,25  2,4 2  0,25  2,4  0,65 ;
2 5
2 5
1  4 
3 7;
16) 3 72
2 2
 2
1   1 
7 7
 7
1,9  3,8  1,9  1,2
17)
;
0,2 2  0,2  1,7
14) 27 2  2  27  13  13 2
15) 0,16  6,41  1,25  0,16  1,25 2  0,16 2  1,25 ;
5 7
7 8
1   
15 9 ;
16) 9 15
2
2 1
 2
1   1 
5 15
 5




5
4




18) 14,9  1,25  0,75  1,1  14,9  0,75  1,1  1,25 ;
1,7  1,6  1,7 2
;
3,4  8,7  3,4  5,4
1 1
2
1 4
2
18) 3  4  4,2   3  2  2,8  ;
3 5
3
3 5
3
19) 19,9  18  19,9  16  30,1  18  30,1  16 ;
19) 77,3  13  8  37,3  77,3  8  13  37,3 .
59 3  413
 59  41 ;
20)
18
 97 3  533

 97  53  : 152,5 2  27,5 2 ;
21) 
44




 57 3  333

 57  33  ;
22) 36,5 2  27,5 2 : 
90




17)
67 3  52 3
 67  52
119
 79 3  413

 79  41 : 133,5 2  58,5 2
21) 
38


20)


 69 3  29 3

 69  29  ;
22) 94,5 2  30,5 2 : 
98




2
II Упростите выражение и найдите его значение.
1) a  3  a  2 a  2 
2
при a = -3,5;
2) 3 p  8  4 p  6  100 p при p = -2;
2
2


1
3) 127  5c  3 25c 2  15c  9 при c =  1 ;
5
4) ax-2a-3x+6
при а = 1,5; x = 3,5;
5) 2a  b  2a 2  ab при а = - 1; b = 998;
1) х  3  х  3х  3 при х= -0,1;
4
2
2
2) 13  5m   12  4m   4m при m = ;
3
2
3) 64  4  3a  16  12a  9a 2 при а =  ;
3
2
5
4) 7by  4b  14 y  8 при b  , у =
;
28
7
5) 5ab  7b  5a 2  7 a при a = 3,7; b =-3,7
2

6)
а 2  2а
при а = -108
6  3а
6)
с 2  4с
при с = 24
12  3с
7)
3b 2  9b
при b = 3,1
b2  9
7)
x2  9
при х = 3
3x 2  x 3
8)
x6
при х = 94
2
x  12 x  36
8)

z 2  8 z  16
при z = -16
z 2  16
y 2  14 y  49
9)
при y = -4
y7
t 2  100
9) 2
при t = -8
t  20t  100
10)
15c 2  10cd
при c = -6, d = 4
8d 2  12cd
11)
c 3  27
при с = 15
c 2  3c  9
10)
11)
25 z 2  20 zt
при z = -3, t = -2
16t 2  20 zt
b 2  2b  4
1
при b =
3
3
b 8
12) Пусть x1  x2  7 , x1  x2  2 . Вычислите: x1  x22  x12  x2 ; x12  x 22 ; x12  x1  x2  x22 ;
x13  x23
13)Пусть x1  x2  5 , x1  x2  3 .Вычислите: x1  x22  x12  x2 ; x12  x 22 ; x12  x1  x2  x22 ;
x13  x23
III.
1) 7 a 2 b  14ab 2  7 ab ;
2) 4a 2  4ab  b 2 ;
3) 2a  2b  a 2  ab ;
4) m 2  mn  m  mq  nq  q ;
5) 2 3a 2  bc  a4b  3c  ;
6) 5а 3  125ab 2 ;
7) с  ас  а  bb  2a .
8) ax + 3x + 4a + 12
9) 7c2 – c – c3 + 7


Разложите на множители.
1) 9a 3b  18ab 2  9ab ;
2) 16a 2  8ab  b 2 ;
3) 3т  3п  тп  п 2 ;
4) а 2  3аb  a  aq  3bq  q ;
5) 2 a 2  3bc  a3b  4c  ;
6) 63аb 3  7 a 3 b
7) b  cb  c  aa  2c.
8) 3a + 3 + na + n
9) x3 – 6 + 2x – 3x2


3
10) 40a3 + 21bc – 56ac2 – 15a2b2
11) 30x2 + 10c – 25cx – 12x
12) 3x(a + b) + y(a + b)
13) m(x –y) –(x – y)
14) a(b – c) + 3(c – b)
15) a(x – y)2 – (x - y)
16) 9а 2  16b 2
17) 25a 2  70ab  49b 2
18) (x + 1)2 - 25
19) (y + 2)2 - 4y2
20) (6y – 7)2 –(9y + 4)2
1
8 3
21) а 3 
b
8
27
64 3 729 3
22)
c 
d
343
1000
23) a6 – 8
1
24)  x 6 
8
10) 16xy2 – 5y2z – 10z3 + 32xz2
11) 18x2z -10kxy + 20k2y – 36kxz
12) 5p(r – s) + 6q(r – s)
13) (c + 2) – (d(c + 2)
14) 7z(x – y) – 5(y – x)
15) 5(a + 3)3 – (a + 3)
16) 144а 2  25b 2
17) 9a 2  30ab  25b 2
18) (z + 10)2 - 36
19) (t – z)2 - 9t2
20) (15z + 4)2 – (3z – 2)2
125 3 216 3
21)
x 
y
512
343
1
125 3
22)
m3 
n
729
216
23) 27 + b9
1
 y6
24) 
64
IV. Сократите дробь.
x 2  5x  6
ах  ау  bx  by
а)
; б) 2
;
ax  ay  bx  by
x  4x  4
a 2  b 2  c 2  2ab
xz  3 yz
в) 2
; г) 2
;
2
2
x  3 xy
a  b  c  2ac
д)
3m  6n
;
12n  6m
е)
4x 2 y  4x3
;
12 x 2 y 2  12 xy3
a 2  3a  2
аc  bc  ad  bd
а)
; б) 2
;
ax  ay  bx  by
a  6a  5
x3  x2  x  1
s2  s
в)
;
г)
5s  5
x 4  2x 2  1
4
2nd  4 pd 4
2 p  4q
д)
; е)
16q  8 p
3nd 3  6 pd 3
y 2  144
1  5 y  25 y 2
ж)
;
з)
;
12 y  y 2
125 y 3  1
ж)
c 2  5c
4t 2  2t  1
;
з)
;
25  c 2
8t 3  1
9  6x  x 2
8t 3  125
и)
; к)
;
x3
4t 2  25
и)
16 z 2  9
5  2m
;
к)
;
4m 2  20m  25
27  64 z 3
3qp 2  27q
x6  y6
л)
;
м)
27q  p 3 q
x3  y3
л)
8тn 2  2m
y6  y3
;
м)
8mn 4  mn
y6 1
4
V. Решите уравнение.
2х  7 х  3

 4х ;
3
2
3х  1 2 х  1 х
б)


1;
7
2
14
2
2
в) 2  3х   1  4 х   5 х  15 х  1 ;
3 х  11 2 х  7

 4х ;
2
3
2 х  1 х 3х  1
б)


1;
5
15
3
2
2
в)  х  1  2 х  3  5 х  1х  1 ;
г) х 3  2 х 2  9 х  18  0 .
у 1 у  5
д)

у 1 у  3
е) 16 y  y 3  0
ж) d 3  d  0
9
81
0
з) c 2 
16
100
2
и) 5 z  3  9  0
а)
а)
г) х 3  3х 2  4 х  12  0
х
х2
д)

х5 х6
е) x 3  x  0
ж) c 3  c 2  0
4 2 16
b 
0
з)
49
121
2
и) 2 x  5  36  0
к) x 2  24 x  144  0
2x  1
1
л)
5
7 x  3 5x  1

м)
6
2
2 x  1 3 x  19

н) 3x 
5
5
o) 6x(x + 2) – 0,5(12x2 – 7x) – 31 = 0
p) m(m + 1)(m + 2)=0
r) n2(n – 3)(n – 8)=0
к) 25 x 2  60 x  36  0
11  3 x 1

л)
4
2
3x  7 6 x  4

м)
5
10
2x  3 x  6

н) 2 x 
3
3
о) 2x3 – x(x2 – 6) – 3(2x -1) – 30 = 0
p) p(p + 13)(p – 17)=0
r) q2(q – 21)(q – 105)=0
VI. Решите систему уравнений.
х  2  у
а) 
3х  2 у  9
2 х  у  15
в) 
3х  у  9
 у  2х  1
д) 
у  5  х
2 х  у  8  0
б) 
3х  4 y  7  0
х  2 у  5
г) 
2 х  у  5
 у  11  2 х
а) 
5 х  4 у  8
 х  3 у  17
в) 
2 у  х  13
4 х  2 у  6
е) 
3 х  у  7
 у  3х  7
д) 
у  7  х
3х  4 у  2  0
б) 
5 у  х  6  0
х  3 у  6
г) 
2 х  у  7
5 х  3 у  6
е) 
2 х  7 у  13
40 x  3y  -10
 3x  4 y  24
ж) 
з) 
20x - 7y  -5
5 x  3 y  40
10х  15y  -45
 5x  3y  -15
ж) 
з) 
2x - 3y  33
2x  7y  47
1
1
4 x  15 y  42
 x  y 1
и) 
к)  2
3
 6 x  25 y  32
6 x  5 y  3
1
1
 4 x  3 y  4
12 x  35 y  25
и) 
к) 
 8 x  15 y  55
4 x  3y  7
 5
5
VII. Функции и графики
1. Прямая у = kx+b проходит через точки А(1; 5) и В(- 2; - 1).
а) Найдите числа k и b и запишите уравнение прямой.
б) Принадлежит ли этой прямой точка С(64; 126).
в) Найдите точки пересечения графика данной функции с графиком функции у  х 2 .
2. Прямая у = kx+b проходит через точки А(- 1; 4) и В(- 2; 6).
а) Найдите числа k и b и запишите уравнение прямой.
б) Принадлежит ли этой прямой точка С(25; - 78).
в) Найдите точки пересечения графика данной функции с графиком функции у  х 2 .
1
3. Графики линейных функций у  2 х , у  х и у  4  х , попарно пересекаясь,
3
образуют треугольник.
а) Постройте графики данных функций.
б) Используя график, определите координаты вершин треугольника.
в) Найдите координаты точки пересечения медиан данного треугольника.
г) Какому из графиков принадлежит точка А(-1,5; 3) .
1
4. Графики линейных функций у  3 х , у  х и у  4 х  7 , попарно пересекаясь,
2
образуют треугольник.
а) Постройте графики данных функций.
б) Используя график, определите координаты вершин треугольника.
в) Найдите координату точки пересечения медиан данного треугольника.
г) Какому из графиков принадлежит точка А(3; 1,5) .
1
5. Постройте график функции у  х  3 .
2
а) Принадлежит ли графику этой функции точка А(- 2; - 4) (объяснить);
б) Найдите точки пересечения графика данной функции с графиком функции у  х 2 ;
в) Записать формулу линейной функции, график которой проходит через точку В(- 4; 0) и
1
параллелен графику функции у  х  3 .
2
6. Постройте график функции у  0,2 х  4 .
а) Принадлежит ли графику этой функции точка А(- 5; 1) (объяснить);
б) Найдите точки пересечения графика данной функции с графиком функции у  х 2 ;
в) Записать формулу линейной функции, график которой проходит через точку В( 5; 3) и
параллелен графику функции у  0,2 х  4 ..
7. Составьте уравнение прямой, проходящей через заданные точки:
1. А(2;3) и В(-1;4)
3.M(-3;-1) и N(2;5)
2.С(-6;7) и D(4;3)
4.P(6;2) и Q(-1;-3)
8. Найдите координаты точек пересечения графиков с осями координат:
1
3
а) y   x  1
б) y  x  6
3
4
в) y  1,2 x  6
г) y  1,6 x  8
9. Найдите точку пересечения прямых графическим и аналитическим методами:
а) y  3x  4 и y  x
б) y  2 x и y  0,5 x  5
1
в) y  x  3 и y   x  1
г) y  5 x  2 и y  x  4
3
6
VIII. Геометрия.
1. В треугольнике АВС АВ = ВС. На медиане BE отмечена точка М, а на
сторонах АВ и ВС — точки Р и К соответственно. (Точки Р, М и К не лежат на
одной прямой.) Известно, что <BMP=<BMK. Докажите, что:
а) углы BPM и ВКМ равны;
б) прямые РК и ВМ взаимно перпендикулярны.
2. Внутри треугольника АВС взята точка О, причем <BOC = <ВОА, АО = ОС.
а) Докажите, что углы ВАС и ВСА равны.
б) Докажите, что прямая ВО проходит через середину отрезка АС.
3. На высоте равнобедренного треугольника АВС, проведенной к основанию АС, взята точка Р,
а на сторонах АВ и ВС — точки М и К соответственно. (Точки М, Р и К не лежат на одной
прямой.) Известно, что ВМ = ВК.
а) Докажите, что углы BMP и ВКР равны.
б) Докажите, что углы КМР и РКМ равны.
4. На сторонах АВ, ВС, АС равнобедренного треугольника АВС с основанием АС отмечены
точки М, К, Р соответственно так, что <AMP = < РКС и AM = КС.
а) Докажите, что МР = РК.
б) Докажите, что прямые МК и ВР взаимно перпендикулярны.
5. На сторонах АВ, ВС, АС треугольника ABC отмечены точки Т, Р, М соответственно;
<MPC = 51°, <ABC = 52°, <АТМ = 52°.
а) Найдите угол ТМР.
б) Докажите, что прямые МР и ВТ имеют одну общую точку.
6. На прямой последовательно отложены отрезки АВ, ВС, CD. Точки Е и Р лежат по разные
стороны от этой прямой.
< ABE = <PCD =143°, <PBD = 49°, <ACE =48°.
а) Докажите, что прямые BE и PC параллельны.
б) Докажите, что прямые РВ и СЕ пересекаются.
7. Из точек А и В, лежащих по одну сторону от прямой, проведены перпендикуляры АС и BD к
этой прямой; <ВАС = 117°.
а) Найдите угол ABD.
б) Докажите, что прямые АВ и CD пересекаются.
8. На сторонах угла А, равного 43°, отмечены точки В и С, а внутри угла — точка D так, что
<ABD = 137°, <BDC = 45°.
а) Найдите угол ACD.
б) Докажите, что прямые АВ и DC имеют одну общую точку.
9. В треугольнике ABC <A = 90°, <C = 15°. На стороне АС отмечена точка D так, что <DBC =
15°.
а) Докажите, что BD = 2АВ.
б) Докажите, что ВС < 4АВ.
10. В треугольнике ABC <C = 60°. На стороне АС отмечена точка D так, что <BDC = 60°, <ABD
= 30°.
а) Докажите, что AD = ВС.
б) Докажите, что периметр треугольника ABC меньше пяти длин отрезка ВС.
11. В треугольнике АВС угол В прямой, BD — высота треугольника.
а) Докажите, что <A= <DBC.
б) Докажите, что если <A < <C, то AD>DC.
IX. Задачи
1. Бригада должна была выполнить заказ за 10 дней. Ежедневно перевыполняя норму на 27
деталей, бригада за 7 дней работы не только выполнила задание, но еще изготовила
дополнительно 54 детали. Сколько деталей в день изготовляла бригада?
7
2. Заказ по выпуску машин завод должен был выполнить за 15 дней. Но уже за два дня до
срока завод не только выполнил план, но и выпустил сверх плана еще 6 машин, так как
ежедневно выпускал по 2 машины сверх плана. Сколько машин ежедневно должен был
выпускать завод по плану?
3. Лодка шла против течения реки 4,5 ч и по течению 2,1 ч. Найти скорость лодки в стоячей
воде, если она прошла всего 52,2 км, а скорость течения реки равна 3 км/ч.
4. Лодка шла по течению реки 2,4 ч и против течения 3,2 ч. Путь, пройденный лодкой по
течению, оказался на 13,2 км длиннее пути, пройденного против течения. Найти скорость
лодки в стоячей воде, если скорость течения реки равна 3,5 км/ч.
5. Собранный виноград предполагалось уложить в ящики, по 9,2 кг в каждый. Вместо этих
ящиков взяли другие, вмещающие по 13,2 кг каждый, и тогда потребовалось на 50
ящиков меньше. Сколько килограммов винограда было уложено?
6. Расстояние между станциями А и В пассажирский поезд проходит на 45 мин. быстрее,
чем товарный. Определить расстояние между этими станциями, если известно, что
скорость движения пассажирского поезда равна 48 км/ч, а товарного – 36 км/ч.
7. Кооператив продавал рабочие брюки и куртки. Брюки стоил на 150 р. дешевле куртки.
На распродаже цена на брюки была снижена на 20%, а на куртку – на 10%, и теперь
брюки и куртку можно было купить за 645 р. Сколько стоили брюки, и сколько стоила
куртка до распродажи?
8. Один рабочий в день выпускал на 50 деталей меньше другого. Когда выработка первого
повысилась на 1% в день, а второго - на 2%, они стали вместе выпускать в день 254
детали. Сколько деталей в день выпускал каждый рабочий первоначально?
9. Туристы в первый час прошли 3 км. Если бы они продолжали двигаться с той же
скоростью, то опоздали бы к месту сбора на 40 мин, поэтому они увеличили скорость на
1
и пришли к месту сбора за 45 мин до назначенного срока. Какое расстояние прошли
3
туристы до места сбора и за какое время?
10. Первый час автомобилист ехал со скоростью 50 км/ч и рассчитал, что если он и дальше
будет ехать с той же скоростью, то опоздает в город на полчаса. Он увеличил скорость на
20% и прибыл в город вовремя. Какой путь проехал автомобилист и за какое время?
11. Некоторое число уменьшили на 15%, а затем результат увеличили на 10%. После этого
получили число, которое на 13 меньше первоначального. Найдите первоначальное число.
12. Задуманное число сначала увеличили на 12%, а затем результат уменьшили на 24%.
Полученное при этом число оказалось на186 меньше задуманного. Найдите задуманное
число.
13. Имеются две отливки стали двух сортов, одна из которых содержит 5%, а другая – 10%
никеля. Сплавив их вместе, получили отливку, содержащую 8% никеля. Найдите массу
каждой отливки до переплавки, если известно, что вторая отливка содержала никеля на
4т больше, чем первая.
14. Имеется лом стали двух сортов с содержанием 5% и 40% никеля. Сколько тонн стали
каждого сорта нужно взять, чтобы, сплавив их, получить 140т стали, в которой
содержится 30% никеля?
15. Отношение двух чисел равно 2:3, а сумма этих чисел равна 135. Найдите эти числа.
16. Отношение двух чисел равно 7:4. Найдите эти числа, если одно из них больше другого на
48.
17. Одна из сторон треугольника в 2 раза меньше другой стороны и на три сантиметра
меньше третьей. Найдите стороны треугольника, если его периметр равен 31 см.
18. В треугольнике один угол в три раза меньше другого угла и на 20°больше третьего.
Найдите углы треугольника.
3
19. Сторона АВ треугольника АВС составляет стороны ВС, а сторона АС на 2 см больше
4
ВС. Найдите стороны треугольника, если его периметр равен 24 см.
8
20. Найдите углы треугольника, если их отношение равно 2:3:4.
21. Моторная лодка за 2 часа по течению реки проплывает такое же расстояние, что и за 3
часа против течения. Найдите собственную скорость лодки, если скорость течения реки
равна 3км/ч.
22. Катер шел по течению реки 5ч, а затем против течения 3ч. Найдите собственную
скорость катера, если известно, что скорость течения реки 3км/ч, а всего пройдено 126
км.
23. Из пунктов А и В одновременно навстречу друг другу выехали два велосипедиста и
встретились через 40 мин. Скорость одного из них на 3 км/ч больше скорости другого.
Найдите скорости велосипедистов, если расстояние между пунктами А и В равно 18 км.
24. Из городов А и В, расстояние между которыми 350 км, одновременно навстречу друг
другу выехали два мотоциклиста. Через три часа после начала движения им осталось
проехать до встречи 20 км. Найдите скорости мотоциклистов, если скорость одного из
них на 10 км/ч меньше скорости другого.
25. Из пункта А в пункт В со скоростью 60 км/ч выехал мотоциклист. Через 30 мин.
навстречу ему из В выехал другой мотоциклист, скорость которого составляла 50 км/ч.
Какое время ехал второй мотоциклист до встречи с первым, если расстояние между
А и В равно 162 км?
26. Из пункта М в пункт К выехал автобус. Через полчаса из К в М со скоростью,
превышающей скорость автобуса на 18 км/ч, выехал легковой автомобиль. Через 1 час 20
мин после своего выхода он встретил автобус, причем проехал расстояние, на 3 км
большее, чем автобус. Чему равно расстояние между М и К?
27. От пристани А отошел плот. Одновременно с ним от пристани В отошла моторная лодка
вверх по течению реки, по направлению к А. Найдите собственную скорость лодки, если
лодка и плот встретились через 2 часа, а расстояние между пристанями А и В равно 16
км.
28. От пристани А вниз по течению реки отошла лодка, собственная скорость которой равна
12 км/ч, а через один час вверх по течению реки отправился катер, собственная скорость
которого равна 18 км/ч. Найдите скорость течения реки, если через три часа после
выхода лодки расстояние между лодкой и катером составляло 75 км.
29. За 3 м одной ткани и 6 м другой заплатили 900 р. Сколько стоит один метр каждой ткани,
если 9 м первой ткани стоят столько же, сколько 12 м второй?
30. За 2 кг конфет и 3 кг печенья заплатили 480 р. Сколько стоит 1 кг печенья и 1 кг конфет,
если 1,5 кг конфет дешевле 4 кг печенья на 15 р.?
31. Из пунктов А и В расстояние между которыми 360 км, одновременно навстречу друг
друга выехали два автомобиля и встретились через 2 ч 15 мин. Если бы первый
автомобиль выехал на 24 мин. раньше второго, то встреча произошла бы через 2 часа
после выезда второго автомобиля. Найдите скорость каждого автомобиля.
32. Из пунктов А и В. Расстояние между которыми30 км, навстречу друг другу
одновременно вышли два пешехода и встретились через 3 ч 45 мин. Если бы первый
вышел на 2 ч раньше второго, то встреча произошла бы через 2,5 ч после выхода второго.
Найдите скорости пешеходов.
33. Теплоход против течения реки проплывает 96 км за 4 ч, а по течению реки 90 км за 3 ч.
Найдите собственную скорость теплохода.
34. по течению реки катер проходит 28 км за 1 ч 20 мин, а против течения – 24 км за 1,5 ч.
Найдите скорость течения реки.
35. Разность двух чисел равна 52. Если первое число разделить на второе, то в частном
получится 3 и в остатке 4. Найдите эти числа.
36. Сумма цифр заданного двузначного числа равна 7. Если к каждой цифре прибавить по 2,
то получится число, меньшее удвоенного заданного числа на 3. Какое число задано?
37. Первое число составляет 25% второго. Найдите эти числа, если их сумма равна 52,2.
9
38. Первое число составляет 87% второго. Найдите эти числа, если второе число больше
первого на 3,9.
39. Первое число составляет 124% второго. Найдите эти числа, если их сумма равна 112.
X. Разное
1. Дана точка М(1,5). Найдите координаты точек L и N таких, что MN=2ML, NL=0,5.
Сколько решений имеет задача?
2. Дана точка К(-1). Найдите координаты точек P и M, таких, что PM=8 и KP=3KM
3. Постройте:
а) ∆АВС, если А(6;0), В(2;-3), С(3;2)
б) ∆ А1 В1С1 , симметричный ∆АВС относительно оси Х;
в) ∆ А2 В2С2 , симметричный ∆АВС относительно оси У;
г) ∆ А3 В3С3 , симметричный ∆АВС относительно начала координат.
4. Известны координаты двух противоположных вершин квадрата ABCD: A(2;-2), C(-2;2).
Найдите координаты двух других вершин. Сколько решений имеет задача?
5. Длина стороны квадрата ABCD равна 6, а координаты вершины А равны (-2;3). Найдите
координаты остальных вершин, зная, что сторона АВ квадрата параллельна оси ординат
и что начало координат лежит внутри квадрата.
6. Квадрат со стороной 8 расположен так, что центр его находится в начале координат, а
стороны параллельны осям координат. Определите координаты вершин квадрата.
1
3
7. На графике линейной функции y  x  2 найдите точку, абсцисса и ордината которой
2
4
– противоположные числа.
3
1
8. На графике линейной функции y   x  3 найдите точку, абсцисса и ордината
4
2
которой – одинаковые числа.
9. Для двух линейных функций y  k1 x  b1 и y  k 2 x  b2 подберите такие коэффициенты
k1 , k 2 , b1 , b2 , чтобы их графики пересекались в первом координатном угле, и одна из
функций была бы убывающей, а вторая возрастающей.
10. Для двух линейных функций y  k1 x  b1 и y  k 2 x  b2 подберите такие коэффициенты
k1 , k 2 , b1 , b2 , чтобы их графики пересекались во втором координатном угле, и обе
функции были бы убывающими.
 3x  2 4
 4 y  3  15

11. Решите систему уравнений: 
5x  y  1
 3 y  2
 4x  5
5x  2 y  1

12. Решите систему уравнений: 
3  2x  1
1  2 y 5
13. Решите уравнение:
x   x   1
а)
x   x  x 
x  : x   1
б)
x  : x
8 4
15 4
45 2
5 4
5 9
4 4
5
40 2
17
а)
x17  x 23
 243
x   x  x 
x   x   x  512
б)
x : x 
8 3
5 2
130
2 3
5
4 7
25 4
10
2 x 5  2 x 3  2  3
4 x 3  8 x 4
3
г) 3x 3  24 и 3 x   27
5 x 7  5 x 4  25  100
в)
в)
д) 2 х5  1
г) 5 x 5  1215 и 5 x   100000
д) 5 х 3  1
х
25x 
2 4
 125 x 2
5
х
1
7
е)    1
е)    1
3
9
3 х4
 243
ж) 3
ж) 2 45 х  512
5
3
1
з) х 9  х 9  1 х 9  1
з) 2,05 х 7  3,07 х 7  1,03х 7  0,01
7
14
2
14. Представьте число 8000 в виде произведения степеней простых чисел
15. Представьте число 50625 в виде произведения степеней простых чисел
16. Представьте в виде квадрата или куба некоторого одночлена:
2
7
1
а) 2 х 4 у z 8
а) 3 a 6 d 4 c 8
9
16
9 6
б) 0,027m n
б) 0,008u 15v 3
17. Пусть a  3x 2  4 x  8 , b  2 x 2  7 x  12 , c  5 x 2  3 x  27 . По данному ниже условию
составьте выражение и преобразуйте его в многочлен стандартного вида, записанный по
степеням убывания переменной х:
а) 2а - 3с - 4в;
б) 7ах – 12хb + 15хс-13
в) 72ха – 4b + 3хс + 4
г) 0,1х2а + 0,5хс – 0,63b – 17
2
2
18. Пусть х = 3а + 4; у = 12а – 13; z = a – a + 1; k = 5a3; l = 12a2; m = 4a. По данному ниже
условию составьте выражение и преобразуйте его в многочлен стандартного вида,
записанный по степеням убывания переменной х:
а) 2x + ky - lz;
б) lx –3my;
в) kx + ly –mz;
г) mx – lz + 4kx - 14
19. Докажите, что значение выражения:
а) 176+175 кратно 18;
б) 428+427 кратно 43;
17
15
в) 3 +3 кратно 30;
г) 223+220 кратно 72.
20. Докажите, что значение выражения:
а) 87 – 218 кратно 28;
б) 97+312 кратно 90;
в) 106+57 кратно 23;
г) 64 – 28 кратно 13.