РЕШЕНИЯ ЗАДАЧ 9 КЛАССА
реклама
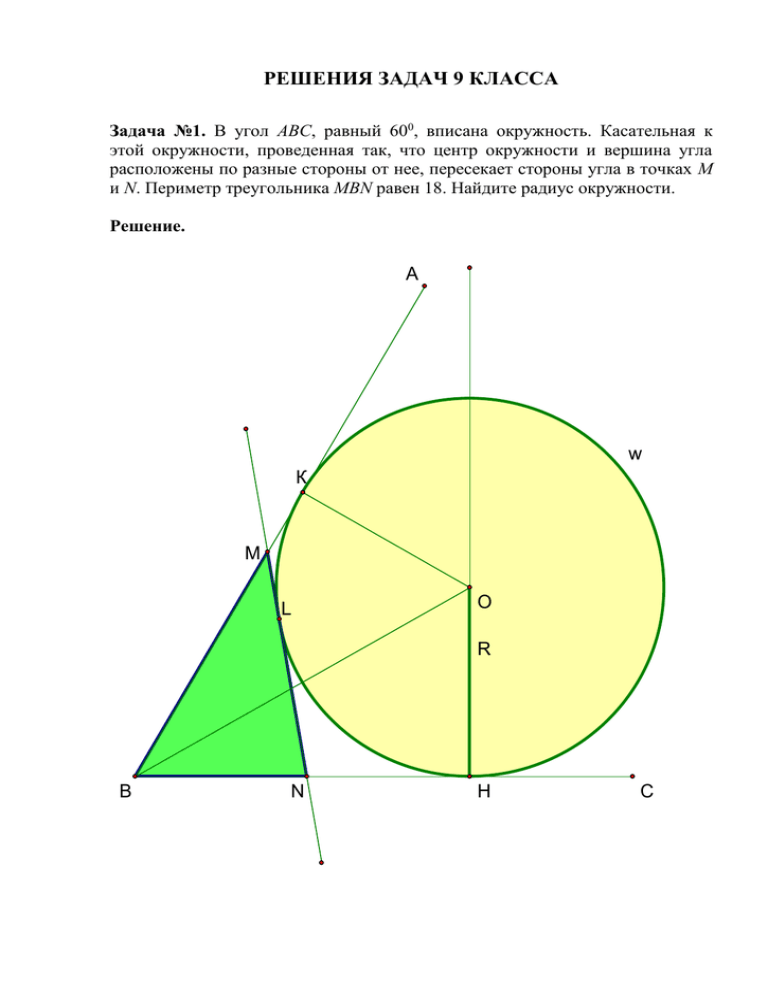
РЕШЕНИЯ ЗАДАЧ 9 КЛАССА Задача №1. В угол АВС, равный 600, вписана окружность. Касательная к этой окружности, проведенная так, что центр окружности и вершина угла расположены по разные стороны от нее, пересекает стороны угла в точках М и N. Периметр треугольника МВN равен 18. Найдите радиус окружности. Решение. A w К M L O R B N H C 1. Пусть K и H – точки касания данной окружности и сторон данного угла, а L – точка касания окружности и стороны MN треугольника MBN, тогда MK=ML, LN=HN, т.к. отрезки касательных, проведенных из одной точки к окружности, равны. PMPN BM ( ML LN ) NB ( BM MK ) ( HN NB ) BK BH 18 , 2. т.к. BK=BH, то BH=9. 3. Точка O – центр окружности, вписанной в угол ABC, равноудалена от его сторон и, следовательно, принадлежит биссектрисе этого угла. В таком 1 случае OBH ABC 30 0 . 2 4. OBH : H 90 0 , B 30 0 BO=2OH=2r, BO2 BH 2 OH 2 , 4r 2 81 r 2 3r 2 81 r 2 27 r 3 3 . Ответ: r 3 3 . Задача№2. Докажите, что сумма диаметров окружностей, одна из которых вписана в прямоугольный треугольник, а другая описана около него, равна сумме его катетов. Доказательство. w A N R b O O1 L c r w1 C K a B 1. Так как О – центр окружности, описанной около прямоугольного треугольника, – середина его гипотенузы, то AB=2R, где R – радиус описанной окружности. 2. Пусть L, K и N – точки касания окружности, вписанной в треугольник, и его сторон, тогда BN=BK, AN=AL, CK=CL (отрезки касательных, проведенных из одной точки к окружности, равны между собою) и, следовательно, AL+BK= AL+BN =2R. 3. Пусть O1 – центр окружности вписанной в ABC . Четырехугольник LO1 KC – прямоугольник с равными смежными сторонами ( O1 L O1 K r ). Следовательно, CL CK r , где r – радиус вписанной в ABC окружности. 4. AC BC ( AL BK ) (CL CK ) 2R 2r . Задача№3. Два параллелограмма расположены так, что каждая сторона одного из них содержит по одной вершине другого. Докажите, что центры этих параллелограммов совпадают. Доказательство. L A \ D K O \ В N С M Решение: 1. Рассмотрим два желтых треугольника АКL и CMN. AKL=CMN = как углы с соответственно параллельными сторонами (AK CM, KL MN). Аналогично, равны углы при вершинах L и N. Таким образом, желтые треугольники равны по стороне (KL=MN) и двум прилежащим углам и . 2. Аналогично доказывается равенство другой пары треугольников BNK = DLM. Из равенства этих треугольников следует совпадение длин их сторон BN=DL. 3. Рассмотрим зеленый четырехугольник BLDN. Две его противоположные стороны BN и DN равны и параллельны. Следовательно, BLDN - параллелограмм. Но тогда его диагонали BD и LN точкой пересечения О делятся пополам. 4. Известно, что середина любой диагонали параллелограмма является его центром. Но тогда точка О, как середина синей диагонали BD синего параллелограмма ABCD - его центр. Аналогично, точка О, как середина зеленой диагонали LN зеленого параллелограмма KLMN также является его центром. 5. Итак, центр О синего параллелограмма АВСD совпадает с центром О вписанного в него зеленого параллелограмма KLMN. Задача№4. Четырехугольник ABCD вписан в окружность, центр которой принадлежит диагонали АС четырехугольника. Докажите, что проекции противоположных сторон четырехугольника на его диагональ BD равны между собою. Доказательство. B k _ P A M O Q l F / D 1. Пусть BP и DQ – проекции сторон AB и CD четырехугольника ABCD на его диагональ BD. 2. ABC ADC 90 0 (вписаны в окружность, опираются на диаметр) 3. Рассмотрим ABC и CAD : 1 P D 90 0 , B C AmD 2 BP AB AB DC ABP CAD BP .(1) DC AC AC 4. Рассмотрим CDQ и CBA: Q B 90 0 , 1 DQ DC AB DC D A BnC CDQCAB DQ .(2) 2 AB AC AC Сравнивая (1) и (2), делаем вывод: BP=DQ. Задача№5. В прямоугольнике АВСD сторона АВ в три раза меньше стороны ВС. Точки Р и Q принадлежат стороне ВС и при этом ВР=PQ=QC. Докажите, что сумма углов АРВ, AQB и АСВ равна прямому углу. Доказательство. A1 B P1 P A D1 β Q β γ C D 1. Очевидно, что APB 450 . 2. Докажем, что AQB ACB 450 . a) Четырехугольник симметричен четырехугольнику BA1 D1C BADC относительно BC. б) ÐÐ1 A1D1, P1 A1D1. PP1C : ABQ в) Рассмотрим и B P 90 0 , AB PP1 a , BQ PC 2a ABQ PP1C PCP1 AQB . г) AP1C : AP1 P1C a 2 4a 2 a 5 , AC a 2 9a 2 a 10 AC 2 AP12 P1C 2 AP1C 90 0 (теорема, обратная теореме Пифагора) Так как AP1 P1C , то ACP1 450 . д) 450 , 45 0 90 0 APB AQB ACB . Задача№6. В треугольнике АВС точка О – центр вписанной окружности, O1 – пересечение биссектрис внешних углов при вершинах В и С. Докажите, что окружность, описанная около треугольника АВС, делит отрезок ОО1 пополам. Доказательство. w2 A w O2 O E + B _ \ w1 C M _ K O1 L Пусть М – пересечение окружности, описанной около треугольника АВС, и отрезка ОО1. 1.О – центр окружности, вписанной в ABC , О - пересечение биссектрис ABC , то есть BAO CAO , ACO BCO . 2. СО1 – биссектриса BCK , а значит О1 равноудалена от сторон BC и CK этого угла. ВО1 – биссектриса CBL , значит О1 равноудалена от сторон BC и BL этого угла. B таком случае О1 равноудалена от сторон L A ,K следовательно принадлежит биссектрисе АО этого угла. Таким образом, точки А, О и О1 – точки одной прямой. 1 1 3. OCO1 ACB BCK 180 0 90 0 . 2 2 4. COM - внешний угол AOC . COM . 5. BCM BAM ( вписаны в окружность, опираются на дугу BM), тогда OCM . 6. OCM : COM OCM MO MC . 7. OCO1 : C 90 0 , O OCM , тогда MO1C 90 0 ( ) , MCO1 90 0 ( ) MO1C O1CM CM MO1 . 8. OM CM , MO1 CM OM MO1 , то есть М – середина ОО1.

