БАЛАНСИРОВКА ЗАРГУЗКИ МАРШРУТИЗАТОРОВ В СЕТЯХ, УПРАВЛЯЕМЫХ ПРОТОКОЛОМ RIP

БАЛАНСИРОВКА ЗАРГУЗКИ МАРШРУТИЗАТОРОВ В СЕТЯХ, УПРАВЛЯЕМЫХ
ПРОТОКОЛОМ RIP
И.И. Труб
Сургутский государственный университет, г.Сургут
Введение
В протоколах маршрутизации дистанционно-векторного типа [3, 4] каждый маршрутизатор периодически
и широковещательно рассылает по сети вектор, компонентами которого являются расстояния от данного
маршрутизатора до всех известных ему сетей. Под расстоянием обычно понимается число шагов. При получении
вектора от соседа маршрутизатор наращивает расстояние до указанных в векторе сетей на расстояние до данного
соседа. Получив вектор от соседнего, каждый маршрутизатор
добавляет к нему информацию об известных ему других сетях, о
которых он узнал непосредственно или из аналогичных
объявлений других маршрутизаторов, а затем снова рассылает
новое значение вектора по сети. В конце концов, каждый
маршрутизатор узнает информацию обо всех имеющихся в
интерсети сетях и о расстоянии до них через соседей. Хорошо
известный и простой в реализации протокол динамической
маршрутизации RIP[6], хотя и вытеснен к настоящему времени в
крупных сетях протоколами состояния канала (OSPF), все же
остается в действии для сетей малого и среднего размера.
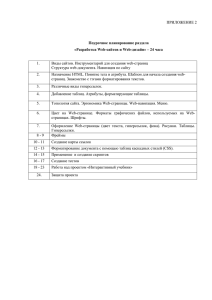
Рис. 1. Пример топологического графа сети.
Поэтому он по-прежнему является объектом изучения
Вершины оответствуют маршрутизаторам,
специалистов, и работы, посвященные связанным с ним
ребра – отдельным сетям.
проблемам, продолжают появляться. Проблемы эти хорошо
известны специалистам – зацикливание, гонки, счет до
бесконечности [1], синхронизация обмена служебными сообщениями[5]. В работе рассматривается еще одна
содержательная задача, которая до настоящего времени не нашла отражения в литературе. Речь идет об
инициализации динамических маршрутных таблиц в маршрутизаторах (узлах) после включения питания и
подсоединения в общую сеть. Эта задача возникла на практике при расширении локальной сети Сургутского
государственного университета и связанном с ним переходе со статической маршрутизации на динамическую.
Проблема заключается в том, что алгоритм формирования маршрутных таблиц не является
детерминированным при одновременном включении всех сетевых интерфейсов всех узлов, и является тем более
случайным, чем выше избыточная связность графа сети. При этом нагрузка на узлы может оказаться сильно
неравномерной. Предлагаемый алгоритм позволяет значительно повысить вероятность формирования таблиц,
обеспечивающих распределение нагрузки, близкое к оптимальному. Слово "близкое" употреблено здесь, потому
что, как будет далее показано, при определенных условиях гарантировать оптимальный результат в принципе
невозможно без ручного редактирования таблиц системным администратором. Рассмотрим простой пример. Для
сети, изображенной на рис.1, протокол RIP может сформировать следующие, абсолютно корректные с точки зрения
спецификации протокола, таблицы.
Для M1
Для M2
Для M3
Для M4
S12 1 S23 1 S23 1 S14 1 S14 1 S12 1 S34 1 S34 1 S24 2 M2
S24 1 S24 2 M2
S24 1 S23 2 M2
S14 2 M4
S12 2 M2
S12 2 M2
S34 2 M4
S34 2 M4
S14 2 M4
S23 2 M2
Из них видно, что вполне возможным является такое распределение, когда маршрутизаторы 1 и 3 не
выполняют никакой работы по перенаправлению трафика, т.е. фактически не нужны, между тем как 2 и 4
перегружены. Это не может считаться удовлетворительным результатом, а ведь его вероятность при
одновременном включении весьма высока , т.к., например, невозможно предсказать, какой из маршрутизаторов –
М4 или М1 раньше даст знать о себе М2. Для того, чтобы обеспечить равномерное, насколько это возможно,
распределение нагрузки, необходимо включать сетевые интерфейсы не одновременно, а один за другим с
некоторым интервалом времени. Делать это можно программно, например, в UNIX-системах с помощью команды
ifconfig.
3
Формализация
Представим всю сеть в виде неориентированного графа, в котором каждый узел соответствует
маршрутизатору, ребра – обслуживаемым этими маршрутизаторами сетям. Каждое ребро, инцидентное некоторому
узлу, соответствует его отдельному сетевому интерфейсу, т.е. сети, трафик которой он может маршрутизировать.
На самом деле в одну сеть могут входить не два, а больше маршрутизаторов, таким образом, лучшим
представлением будет гиперграф [2]. Однако, гиперграфовое представление лишь сделает более громоздкими
обозначения, практически не влияя на решение задачи. Для характеристики загрузки узла введем понятие индекса
узла, который определяет, сколько перенаправлений сетевого трафика он производит. Ясно, что индекс может
варьировать в некоторых пределах. Дадим точные определения этих пределов. Пусть X(A)={X1, X2,:, Xn} –
множество узлов, инцидентных узлу A. Верхним индексом Itop(A) назовем число число всех упорядоченных
паросочетаний множества X, которое равно n(n-1). Это максимальное число переключений трафика, которое может
быть возложено на узел A. Обозначим теперь Xtop(A) множество, обладающее следующими свойствами:
1. элементами Xtop(A) являются все возможные упорядоченные пары {Xi, Xj} вершин, каждая из которых входит
в X(A);
2. не существует вершины Y не равно A, инцидентной одновременно Xi и Xj;
3. вершины Xi и Xj не смежны.
Мощность множества Xtop(A) назовем нижним индексом Ibot(A) узла A. Он задает обязательный минимум
переключений, которые должен выполнять узел A. Индексом I(A) узла A (Ibot(A)<=I(A)<=Itop(A)) назовем
реальное число перенаправлений, которые выполняет узел согласно установившимся таблицам маршрутизации.
Иными словами, I(A) – это суммарное количество вхождений узла A в третьем столбце таблиц всех узлов. Заметим,
что Itop и Ibot – статические характеристики, определяемые только топологией сети, а I – динамическая. Например,
для сети на рис. 1 нижние и верхние индексы равны: для M1 – 0 и 2, для М2 – 2 и 6, для М3 – 0 и 2, для М4 – 2 и 6.
В качестве основного показателя распределения нагрузки примем множество индексов I всех узлов сети после
установления таблиц. Задачу поставим следующим образом: при каком порядке включения интерфейсов разность R
между наибольшим и наименьшим элементами множества I будет минимальной? Минимальная разность означает
наиболее равномерное распределение маршрутной нагрузки. Например, для представленных для рис.1 таблиц,
I={0, 6, 0, 4}, R=6, что не является оптимальным значением.
Алгоритм.
При формировании последовательности включения интерфейсов будем исходить из значений верхнего и
нижнего индексов не узлов, а их интерфейсов, определения которых введем по аналогии. Верхним индексом
Itop(A_B) интерфейса A_B узла A, где B – узел, смежный с A, назовем максимальное количество перенаправлений
трафика в одну и другую сторону, проходящих через этот интерфейс. Равен верхний индекс 2*(n-1). Нижним
индексом Ibot(A_B) интерфейса A_B узла A назовем количество элементов (пар) множества Xtop(A), в которые
входит вершина B. Предлагаемый ниже полиномиальный алгоритм включения является эвристическим, т.к.
алгоритм с гарантированным достижением оптимальности, если и возможен, носит переборный характер. Отметим,
что статичная последовательность включений, определенная только по графу сети, не может дать
удовлетворительного результата. Это связано с тем, что после включения очередного интерфейса и модификации
таблиц маршрутизации индексы не включенных пока интерфейсов меняются, а именно – может уменьшиться
верхний индекс, т.к. часть необязательной работы может оказаться назначенной другим интерфейсам а значит,
оставшейся к назначению работы будет меньше. Это изменение следует учесть при выборе следующего
интерфейса. Поэтому последовательность, близкую к оптимальной, нужно строить путем динамического
пошагового пересчета таблиц и индексов:
1. Формируем список верхних и нижних индексов интерфейсов, которым соответствуют оконечности ребер графа
сети.
2. Упорядочиваем интерфейсы по возрастанию разности верхнего и нижнего индексов.
3. Интерфейсы с одинаковой разностью индексов упорядочиваем по возрастанию среднего (нижнего, верхнего)
индекса.
4. Первый интерфейс вычеркиваем из упорядоченной последовательности и заносим в итоговую, определяющую
порядок включения.
5. Меняем таблицы маршрутизации в каждом узле. Алгоритмы этих изменений соответствуют описанию
протокола RIP.
6. Пересчитываем верхние индексы невычеркнутых интерфейсов и переходим к п.1.
Если невычеркнутых интерфейсов больше нет – оптимальная последовательность построена.
4
Приведем теперь алгоритм, детализирующий пункт 6, а именно – процесс пересчета верхних индексов
невключенных интерфейсов. После выполнения пункта 5 в таблицах маршрутизации выделяем новые записи вида:
Mi:
Sjk
2
Sj
Для каждой такой записи выполняем следующее:
6а) Если узлы i и k не являются смежными, не делать ничего – альтернативного пути длины 2 из узла i в
сеть jk не существует. Иначе – перейти к пункту 6б.
6б) Для тех из интерфейсов ki и kj, которые являются невычеркнутыми (невключенными), уменьшить
значение текущего верхнего индекса на единицу – переключение с интерфейса ki на kj маршрутизатор K
осуществлять не будет.
Предложенный алгоритм был протестирован с удовлетворительными результатами на множестве примеров
путем имитационного моделирования и в локальной сети СурГУ. Результаты тестов не могут быть приведены здесь
ввиду ограниченного объема данной публикации.
ЛИТЕРАТУРА:
1.
2.
3.
4.
5.
6.
Кульгин М. Технологии корпоративных сетей. – СПб, "Питер",
2000.
Лекции по теории графов (В.А.Емеличев и др.) – М.: Наука, 1990.
Олифер В.Г., Олифер Н.А. Компьютерные сети. – СПб, "Питер", 2000.
Cеменов Ю.А. Протоколы и ресурсы Internet. – М.: Радио и связь, 1996.
Floyd S., Jacobson V. The Synchronization of Protocol Routing Messages – IEEE/ACM, Transactions on Networking,
2(2), April, 1994.
Hedrick C. Routing Information Protocol / RFC 1058, June, 1988.
5