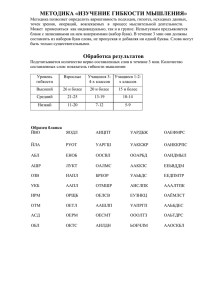
ÐŸÐ°Ñ€Ð°Ð¼ÐµÑ‚Ñ€Ð¸Ñ‡ÐµÑ ÐºÐ¸Ð¹ механичеÑ
реклама
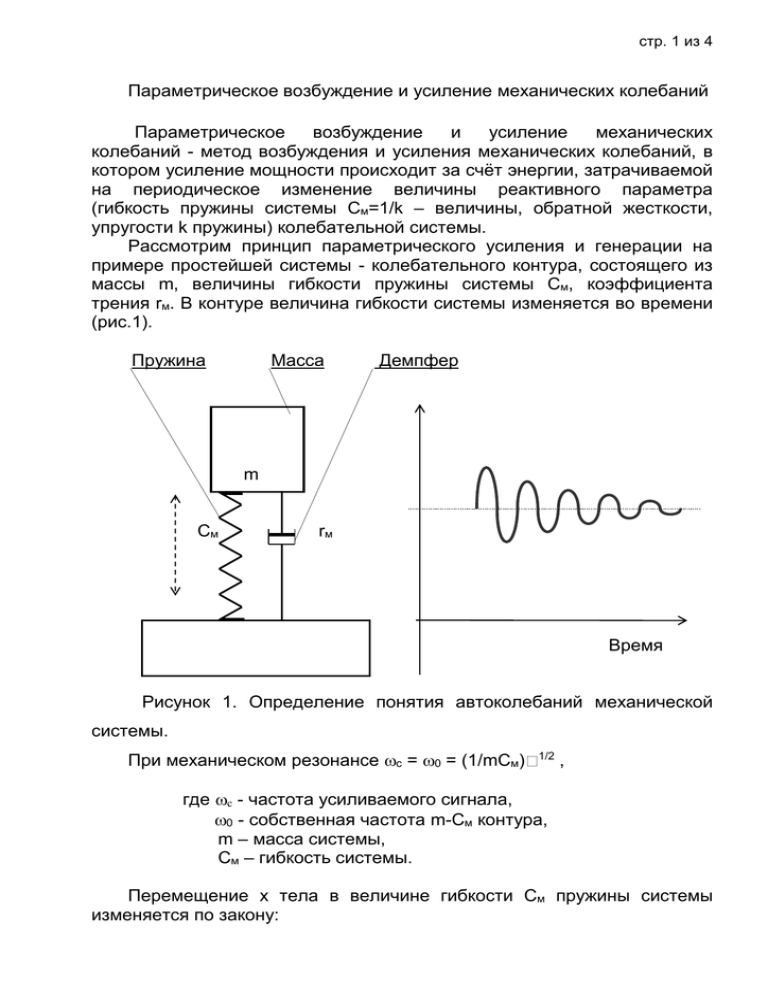
стр. 1 из 4 Параметрическое возбуждение и усиление механических колебаний Параметрическое возбуждение и усиление механических колебаний - метод возбуждения и усиления механических колебаний, в котором усиление мощности происходит за счёт энергии, затрачиваемой на периодическое изменение величины реактивного параметра (гибкость пружины системы См=1/k – величины, обратной жесткости, упругости k пружины) колебательной системы. Рассмотрим принцип параметрического усиления и генерации на примере простейшей системы - колебательного контура, состоящего из массы m, величины гибкости пружины системы См, коэффициента трения rм. В контуре величина гибкости системы изменяется во времени (рис.1). Пружина Масса Демпфер m См rм Время Рисунок 1. Определение понятия автоколебаний механической системы. При механическом резонансе с = 0= (1/mCм) 1/2 , где с - частота усиливаемого сигнала, 0 - собственная частота m-Cм контура, m – масса системы, См – гибкость системы. Перемещение x тела в величине гибкости См пружины системы изменяется по закону: стр. 2 из 4 x = x0 * sin с t = Cм * D * A0 sin с t (1) Здесь x – начальное смещение тела от состояния равновесия, м A0 - амплитуда сигнала, м; D = 1/rм (m/Cм)1/2 = f0/f - добротность механического контура. Потенциальная энергия П, запасаемая в пружины системы, равна: величине гибкости П = (x2 / 2 * См) = (x20 / 4 * См) * (1- cos с t). (2) Из (2) видно, что потенциальная энергия П изменяется с частотой, равной удвоенной частоте сигнала (силы). Если в момент, когда x = x0, величина гибкости пружины системы См скачком изменить на См (например, изменить расстояние между точками объекта), то перемещение x не успеет измениться, а энергия П изменится на величину (если См/См << 1): П = - П * См/См. (3) Рисунок 3. Графики накачки и усиления сигнала в параметрическом механическом усилителе. Отсюда следует, что результирующее увеличение энергии в контуре при периодическом изменении См максимально, если уменьшать величину гибкости пружины системы в моменты, когда Cм максимально, а возвращать величину гибкости пружины системы при x = 0. Это означает, что если изменять См с частотой н = 2 с и с определённой фазой, то устройство (фактически это колебания по горизонтали), стр. 3 из 4 изменяющее См, как бы «накачивает энергию» в контур дважды за период колебаний. Если, наоборот, увеличивать гибкость системы См в моменты минимальных значений x, то колебания в контуре будут ослабляться. В более общем виде условие эффективной накачки имеет вид: н = 2 c / n, где n = 1, 2, 3… и т.д. При n = 1 См изменяется каждые четверть периода сигнала (Тс / 4), при больших n - через время, равное nТc / 2. Простейший одноконтурный механический усилитель обычно представляет собой колебательную систему, где величина гибкости пружины системы См изменяется в результате воздействия гармонической силы от генератора накачки на объект, величина гибкости системы которого зависит от величины приложенной к нему силы. Коэффициент усиления параметрического механического усилителя по мощности приближённо равен: Кус = 1 / [(1 – (m/2) * D)] где m = (См макс - См мин)/(См макс + См мин) называется глубиной изменения величины гибкости пружины системы. При [(m/2) * D] 1 коэффициент усиления неограниченно растет, при [(m/2) * D] > 1 система превращается в параметрический генератор. Основной недостаток одноконтурного параметрического усилителя - зависимость Кус от соотношения между фазами усиливаемого сигнала и сигнала накачки. Этого недостатка нет у параметрических усилителей, содержащих два контура и больше. В двухконтурном параметрическом усилителе частота и фаза колебаний во втором («холостом») контуре автоматически устанавливаются так, чтобы удовлетворить условиям эффективной накачки энергии. Если холостой контур настроен на частоту х = н - с, то энергия накачки расходуется на усиление колебаний в обоих контурах. В этом случае: К ~ [1 – m/2 * (Dc * Dх)1/2 ] -1. При [m/2 * (Dc * Dх)1/2] 1 усилитель превращается в генератор. Такой усилитель называется регенеративным. При х = н + с, вся энергия накачки и энергия, накопленная в сигнальном контуре, переходят в энергию колебаний суммарной частоты н + с,. Такой параметрический усилитель называется нерегенеративным усилителемпреобразова-телем. Он устойчив при любой массе m тела и имеет широкую полосу пропускания, но обладает малым Кус. Литература стр. 4 из 4 Мандельштам Л. И., Полное собрание трудов, т. 2, М.- Л. 1947. Эткин В. С., Гершензон Е. М., Параметрические системы СВЧ на полупроводниковых диодах, М., 1964. Регенеративные полупроводниковые параметрические усилители (некоторые вопросы теории и расчета), М., 1965. Каплан А. Е., Кравцов Ю. А., Рылов В. А., Параметрические генераторы и делители частоты, М., 1966. Лопухин В. М., Рошаль А. С., Электроннолучевые параметрические усилители, М., 1968.