Математическое ожидание дискретной случайной величины
advertisement
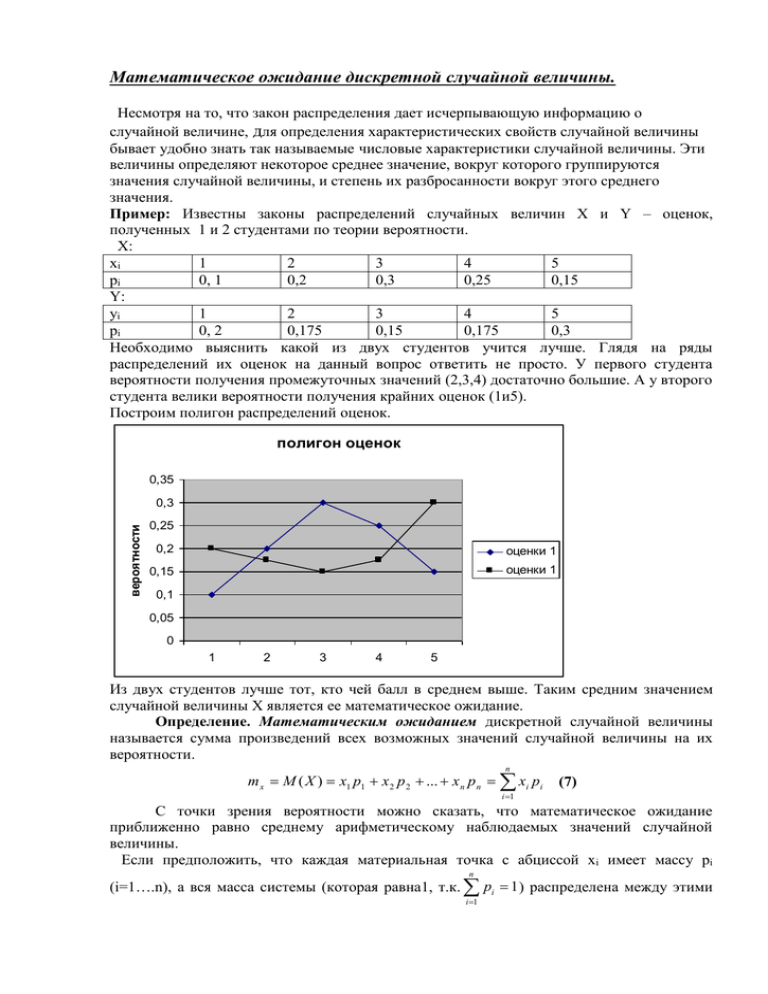
Математическое ожидание дискретной случайной величины. Несмотря на то, что закон распределения дает исчерпывающую информацию о случайной величине, для определения характеристических свойств случайной величины бывает удобно знать так называемые числовые характеристики случайной величины. Эти величины определяют некоторое среднее значение, вокруг которого группируются значения случайной величины, и степень их разбросанности вокруг этого среднего значения. Пример: Известны законы распределений случайных величин Х и Y – оценок, полученных 1 и 2 студентами по теории вероятности. Х: xi 1 2 3 4 5 pi 0, 1 0,2 0,3 0,25 0,15 Y: yi 1 2 3 4 5 pi 0, 2 0,175 0,15 0,175 0,3 Необходимо выяснить какой из двух студентов учится лучше. Глядя на ряды распределений их оценок на данный вопрос ответить не просто. У первого студента вероятности получения промежуточных значений (2,3,4) достаточно большие. А у второго студента велики вероятности получения крайних оценок (1и5). Построим полигон распределений оценок. полигон оценок 0,35 вероятности 0,3 0,25 0,2 оценки 1 0,15 оценки 1 0,1 0,05 0 1 2 3 4 5 Из двух студентов лучше тот, кто чей балл в среднем выше. Таким средним значением случайной величины Х является ее математическое ожидание. Определение. Математическим ожиданием дискретной случайной величины называется сумма произведений всех возможных значений случайной величины на их вероятности. n m x M ( X ) x1 p1 x 2 p 2 ... x n p n xi pi (7) i 1 С точки зрения вероятности можно сказать, что математическое ожидание приближенно равно среднему арифметическому наблюдаемых значений случайной величины. Если предположить, что каждая материальная точка с абциссой хi имеет массу рi n (i=1….n), а вся масса системы (которая равна1, т.к. pi 1 ) распределена между этими i 1 точками, то математическое ожидание представляет абциссу центра масс системы материальных точек. Пример: вычислить М(Х) и М(Y) в задаче о студентах. Решение: По формуле M ( X ) x1 p1 x2 p2 ... xn pn 1 0,1 2 0,2 3 0,3 4 0,25 5 0,15 3,15. M (Y ) y1 p1 y2 p2 ... yn pn 1 0,2 2 0,175 3 0,15 4 0,175 5 0,3 2,65. Т.е. второй студент учится в среднем хуже первого. Свойства математического ожидания. 1) Математическое ожидание постоянной величины равно самой постоянной. М (С ) С (8) Доказательство: Постоянную величину С можно рассматривать как случайную величину, принимающую свое единственное значение С с вероятностью равной 1. Поэтому М(С)=С 1 =1. ▄ 2) Постоянный множитель можно выносить за знак математического ожидания. M (Cx) CM ( x) (9) Доказательство: Случайная величина СХ принимает свои значения Схi с вероятностями рi (i=1…n). n n i 1 i 1 Отсюда M (CX ) (Cxi ) pi C xi pi CM ( X ) . ▄ 3) Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий. M ( XY ) M ( X ) M (Y ) (10) Доказательство: так как величины pij=Р P( X xi ) P(Y y j ) pi p j . Поэтому и X n m независимы, n то m Ì ( ÕY ) xi y j pij xi y j pi p j i 1 j 1 n Y i 1 j 1 m xi pi y j p j M ( X )M (Y ) .▄ i 1 j 1 Это свойство справедливо для произвольного числа случайных величин. 4) Математическое ожидание суммы двух случайных величин равно сумме математических ожиданий слагаемых. M ( X Y ) M ( X ) M (Y ) (11) Это свойство также справедливо для произвольного числа случайных величин. Пример: Известно, что М(Х)=5, М(Y)=2. Найти математическое ожидание случайной величины Z=6X-2Y+9-XY. Решение: М(Z)=6М(Х)-2М(Y)+9-M(X)M(Y)=30-4+9-10=25. Дисперсия дискретной случайной величины. Математическое ожидание не может в достаточной мере охарактеризовать случайную величину. Определение: Дисперсией (рассеиванием) дискретной случайной величины называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания. D( X ) M X M ( X ) . 2 (12) Механическая интерпретация дисперсии заключается в том, что дисперсия представляет собой момент инерции распределения масс относительно центра масс (математического ожидания). Чем меньше дисперсия, тем меньший разброс имеют значения случайной величины относительно математического ожидания. Дисперсия имеет размерность квадрата случайной величины, что не всегда удобною Поэтому в качестве показания рассеивания используют также случайную величину D(X ) . Определение: Средним квадратическим отклонением (стандартным отклонением или стандартом) ( Õ ) дискретной случайной величины Х называется арифметическое значение корня квадратного из ее дисперсии: ( Õ ) = D(X ) . (13) Пример: 1.Дан ряд распределения случайной величины Х. xi 2 4 6 7 pi 0,4 0,3 0,1 0,2 Найти математическое ожидание , дисперсию и среднее квадратическое отклонение случайной величины случайной величины Х. Решение: mx M ( X ) x1 p1 x2 p2 ... xn pn 2 0,4 4 0,3 6 0,1 7 0,2 4 . Выпишем возможные значения для квадрата отклонения случайной величины Х. x1 M ( X )2 (2 4) 2 4 x2 M ( X )2 (4 4) 2 0 x3 M ( X )2 (6 4)2 4 x6 M ( X )2 (7 4)2 9 Тогда Õ M (X ) 2 4 0 4 pi 0,4 0,3 0,1 Дисперсия равна D( X ) 4 0,4 0 0,3 4 0,1 9 0,2 3,8 . 9 0,2 Среднее квадратическое отклонение ( Õ ) = 3,8 1,949 . Как показывает практика, этот способ вычисления дисперсии не очень удобен, потому что при большом количестве значений случайной величины приводит к очень громоздким вычислениям. Поэтому применяется другой способ вычисления дисперсии. Вычисление дисперсии. Теорема. Дисперсия равна разности между математическим ожиданием квадрата случайной величины Х и квадратом ее математического ожидания. 2 D( X ) M ( X 2 ) M ( X ) . (14) Доказательство. Так как математическое ожидание М(Х) математического ожидания М2(Х) – величины постоянные, можно записать: и квадрат D( X ) M X M ( X ) M X 2 2 XM ( X ) M 2 ( X ) 2 M ( X 2 ) 2M ( X )M ( X ) M 2 ( X ) M ( X 2 ) M 2 ( X ). что и требовалось доказать. ▄ Пример: Применим эту формулу для нашего примера: xi 2 4 xi2 4 16 pi 0,4 0,3 6 36 0,1 7 49 0,2 M ( X 2 ) 4 0,4 16 0,3 36 0,1 49 0,2 19,8 D( X ) 19,8 4 3,8 . 2 Свойства дисперсии. 1) Дисперсия постоянной величины равна нулю. D(C ) 0 . (15) Доказательство: D(Ñ ) M Ñ M (Ñ ) M (Ñ Ñ ) 2 Ì (0) 0. ▄ 2) Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат. (16) D(CX ) C 2 D( X ) . Доказательство: 2 D(ÑÕ ) M ÑÕ M (ÑÕ ) M (ÑÕ ÑÌ ( Õ )) 2 Ñ 2 Ì ( Õ M ( X )) 2 C 2 D( X ). ▄ 2 3) Дисперсия суммы двух независимых случайных величин равна сумме дисперсий этих величин. D( X Y ) D( X ) D(Y ) (17) 4) Дисперсия разности двух независимых случайных величин равна сумме дисперсий этих величин. D( X Y ) D( X ) D(Y ) (18). Справедливость этого равенства вытекает из свойства 2. Замечание: обратите внимание, что дисперсия как суммы, так и разности двух независимых случайных величин равна сумме дисперсий этих величин. Пример: Известно, что D(Х)=5, D(Y)=2. Найти математическое ожидание случайной величины Z=6X-2Y+9. Решение: D(Z)=62 D(Х)-22 D(Y)+0=180-8=172. ▄ Математическое ожидание, дисперсия, среднее квадратическое отклонение и другие числа, призванные в сжатой форме выразить наиболее существенные черты распределения называются числовыми характеристиками случайной величины. В теории вероятности эти числовые характеристики играют очень большую роль. Часто вероятностные задачи решают, оперируя только числовыми характеристиками, отставляя в стороне законы распределения случайных величин. Упражнение: дать интерпретацию математического ожидания, дисперсии, среднего квадратического отклонения в анализе меткости стрелка. Если, например, известны распределения Х попаданий в 1,2,3,….10 какого то стрелка за определенный промежуток времени.






