Конечные автоматы

Тема 3: Конечные автоматы
Альтернативный способ определения формальных языков - это их
описание при помощи различных автоматов.
Для регулярных грамматиках допускается описание при помощи
конечных автоматов. Также этот класс грамматик можно описать с
помощью
аналитических
выражений,
называемыми
регулярными
выражениями.
Существуют различные варианты задания конечного автомата.
А) Конечный автомат (КА) можно определить как обьект состоящий из
пяти параметров КА = (Σ , Q, q0, F, δ), где:

Σ - допустимый входной алфавит автомата - конечное множество.

Q ={q0, q1 ,…, qn} - используется для обозначения множества
состояний автомата. Это тоже конечное множество.

q0Q - начальное состояние автомата. В любом конечном автомате
существует только одно начальное состояние.

FQ - используется для обозначения множества конечных или
финальных состояний автомата.

δ :QΣ→p(Q) - функция, определяющая переходы автомата (p(Q) –
подмножества Q).
К примеру следующая конструкция δ(q, a)={q1, q2, …qn} означает что
автомат находящийся в состоянии q, через символ a может перейти в
любое из состояний q1−qn .
Действия автомата просты: принять символы со входной ленты,
передвигая устройство чтения из определённой позиции qi в состояние
qj. Цель - принять слово, написанное на входной ленте.
Работа начинается с состояния q0, считывая по одному символу
входной строки.
Считанный символ переводит автомат в новое состояние из Q в
соответствии с функцией переходов δ. Если по завершении считывания
входного
слова,
автомат
оказывается
в
одном
из
допускающих
состояний из F, то слово принимается. В этом случае говорят, что
данное слово принадлежит языку данного автомата. В противном
случае, слово «отвергается» автоматом.
Пример: Дан КА=(Σ ,Q, q0, δ, F), Σ={0,1}, Q={q0, q1, q2}, F={q2}
δ: δ(q0, 0)={q0}, δ(q0, 1)={q0, q1}, δ(q1, 1)={q2},
δ(q2, 1)={q2}, δ(q2, 0)={q2}.
B) Диаграмма состояний (или иногда граф переходов) - графическое
представление
множества
состояний
автомата
и
функции
его
переходов. Представляет собой нагруженный однонаправленный граф,
вершины которого это состояния КА, ребра - переходы из одного
состояния
в
другое,
а
нагрузка это
символы,
при
которых
осуществляется данный переход. Если переход из состояния q1 в q2
может
быть
осуществлен
при
появлении
одного
из
нескольких
символов, то над дугой диаграммы должны быть надписаны все они.
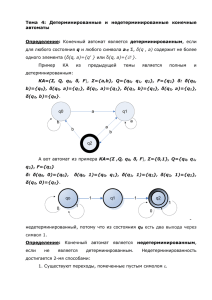
Для примера из п.А) граф переходов будет:
qo
1
q1
1
q2
q2
1
0
1
0
В графе переходов, все финальные состояния обозначаются двойными
окружностями. Промежуточные - просто окружностью.
C) Таблица переходов — табличное представление функции δ. В этой
таблице каждой строке соответствует одно состояние, а столбцу - один
допустимый входной символ. В ячейке на пересечении строки и столбца
записывается действие, которое должен выполнить автомат, если в
ситуации, когда он находился в данном состоянии на входе он получил
данный символ алфавита.
0
1
q0
q0
q0, q1
q1

q2
q2
q2
q2
КА приведенный как пример распозноет следующие слова: 11,
10011001, 00011111, ... Все слова которые имеют по середине 11, а перед
ними сколько угодно цифр 0 и/или 1, и после них тоже самое.
Примеры неправильных слов для данного автомата: 101, 10100, ...
Для автомата можно определить язык (множество слов) в алфавите
Σ,
который
он
представляет/распознает.
Язык,
распознаваемый
конечным автоматом, обозначают L(KA). Данный язык состоит только из
успешных путей, т. е. их распознание начинается из q 0 и завершают
распознание в одном состоянии из F. В данном случае говорится что
конечный автомат KA распознаёт язык L(KA).
Язык L называется автоматным если существует конечный автомат,
распознающий этот язык.
Замечание: Выше было сказано что необходимо в КА чтобы было только
одно начальное состояние. Это утверждение было сделано на основе
следующей леммы:
Лемма: Каждый автоматный язык распознаётся некоторым конечным
автоматом, содержащим только переходы с метками длины единица и
имеющим ровно одно начальное состояние.
Определение: Конфигурацией конечного автомата называется любая
упорядоченная пара (q, x), qQ, xΣ*, x - слово. Конфигурация
представляет
собой
«мгновенное
описание».
Если
представить
что
исходное слово, принадлежность которого рассматриваемому языку надо
проверить, дано в «некотором входном потоке», то в конфигурации (q, x)
слово x это та часть исходного слова, которая пока осталась во входном
потоке, а q текущее состояние автомата. Начальная конфигурация КА это
пара (q0, x).
Конечный
автомат
переходит
из
конфигурации
(q1,
x1 )
в
конфигурацию (qn, xn), если существуют q2, q3, …, qn−1 и x2 ,…, xn−1, так
же существуют переходы: (qi, xi)
(qi+1 , xi+ 1), где i=2, n−1.
Данный переход обозначается (q1, x1)
(qn, xn).
Слово x принадлежит L(KA) только тогда когда существует переход
(q0,x)
(qn,), где qn это одно из конечных состояний. То есть,
множество всех допустимых слов КА составляет L(KA). Или, L(KA)=x /
x Σ*, (q0,x)
(qn,)
Для предыдущего примера КА=(Σ ,Q, q0, δ, F), Σ={0,1}, Q={q0, q1,
q2}, F={q2}
δ: δ(q0, 0)={q0}, δ(q0, 1)={q0, q1}, δ(q1, 1)={q2}, δ(q2, 1)={q2},
δ(q2, 0)={q2}.
qo
1
q1
1
q2
q2
1
1
0
0
Проведем через автомат слово 11. Получается
(q0,11)
1
(q1,1)
11
(q2, ).
А если попытаемся провести через автомат, к примеру слово 101,
получается: (q0,101)
1
(q0,01)
10
(q0, 1)
101
(q1, ) - q1 – это не
финальное состояние, значит данное слово не принадлежит L(KA).
Или, то же слово можно провести через автомат и так: (q0,101)
(q1,01)
10
1
тупик, нет перехода из состояния q1 через 0.
Определение: Автомат называется полным, если его функция перехода
тотальна, т. е. определена на всех парах (q, a) , где qQ, aΣ.
Пример: Следующий КА полный КА=(Σ ,Q, q0, δ, F), Σ={a,b}, Q={q0, q1,
q2}, F={q2} δ: δ(q0, b)={q0}, δ(q0, a)={q1}, δ(q1, a)={q1},
δ(q1, b)={q2}, δ(q2, a)={q1}, δ(q2, b)={q0}.
q0
a
q1
a
b
a
b
b
q2