Факультативное занятие в 11 классе по теме: "Фигуры и тела

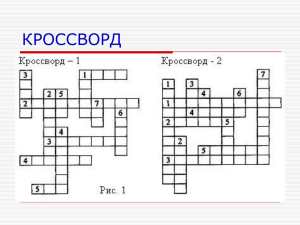
Факультативное занятие в 11 классе по теме: "Фигуры и тела
вращения" с использованием ИКТ.
Выполнил студент группы ФМ-53 Ченцов К.В.
“Предмет математики настолько серьёзен,
что надо не упускать возможности
сделать его немного занимательным”.
Б.Паскаль.
Цели урока:
1) образовательная
-
научить
применять
знания
при
решении
нестандартных задач, видеть в них простые составляющие;
2) развивающая — развитие логического и конструктивного мышления,
самостоятельной способности учащихся.
3) воспитательная – развить аккуратность при
математическую грамотность учащихся, устойчивый
познанию и изучению математики; показать целостность
окружающего мира, взаимосвязь изучаемых предметов,
разделов математики, красоту математики;
построении,
интерес к
и гармонию
взаимосвязь
Тип урока: комбинированный.
 Аппаратные
ресурсы:
компьютеры
с
локальной
сетью,
мультимедийный проектор, экран.
 Программные ресурсы: ИИСС Геометрическое конструирование на
плоскости и пространстве (НФПК).
План – конспект занятия.
I Актуализация знаний.
Игровой момент перед занятием: разгадывание двух кроссвордов
“Тела и фигуры вращения” по группам. Можно завершить в конце
занятия, используя новые знания.
“ Тела и фигуры вращения”
Вопросы к кроссворду – 1
По горизонтали. 1. Фигура на плоскости, все точки которой расположены не
далее данного расстояния от одной точки. 2. Прямая, при вращении которой
вокруг оси образуется боковая поверхность цилиндра, конуса. 3. Тело, полученное
вращением прямоугольника вокруг одной из его сторон. 4. Угол между высотой и
плоскостью основания конуса. 5. Тело, полученное вращением круга вокруг оси,
лежащей в плоскости круга и не пересекающей его.
По вертикали. 1. Тело, полученное вращением прямоугольного треугольника
вокруг одного из его катетов. 2. Плоская фигура, при вращении которой
образуется усечённый конус. 3. Тело вращения, являющееся верхней частью
архитектурного сооружения. 4. Отрезок, соединяющий две точки сферы и
проходящий через центр шара. 5. Тело, полученное вращением полукруга вокруг
его диаметра. 6. Фигура, полученная вращением полуокружности вокруг её
диаметра. 7. Тело вращения, об устойчивости движения которого написана
известная работа великой русской женщины – математика.
Вопросы к кроссворду – 2
По горизонтали. 1. Фигура, полученная вращением параболы вокруг её оси.
2. Отрезок, соединяющий центр сферы с любой её точкой. 3. Круг, являющийся
элементом конуса, плоскость которого перпендикулярна оси конуса. 4.
Музыкальный инструмент, часть которого напоминает Псевдосферу Лобачевского.
5. Отрезок, соединяющий две точки окружности.
По вертикали. 1. Фигура, полученная вращением гиперболы вокруг её оси. 2.
Перпендикуляр, опущенный из вершины конуса на плоскость основания. 3. Тело,
полученное вращением круга вокруг оси, лежащей в плоскости круга и не
пересекающей его. 4. Тело, полученное вращением полукруга вокруг его
диаметра. 5. . Фигура, полученная вращением полуокружности вокруг её
диаметра. 6. Тело вращения, принцип движения которого описала великая
русская женщина-математик. 7. Фигура, полученная вращением эллипса вокруг её
оси.
Эмоциональный настрой.
Великий Омар Хайям – математик, поэт, философ. Он призывает быть
хозяевами своей судьбы. Слушаем отрывок из его произведения:
Ты скажешь, эта жизнь – одно мгновенье.
Её цени, в ней черпай вдохновенье.
Как проведёшь её, так и пройдёт.
Не забывай: она – твоё творенье.
II Формирование новых знаний и способов действия.
Учитель включает проектор и показывает детям с чем они будут работать на
уроке, как устроена данная программа
Конструктор предназначен для построения любых тел и поверхностей вращения.
Позволяет получить тело или поверхность путем вращения произвольной ломаной вокруг
заданной оси.
Полученное тело можно перемещать и поворачивать в пространстве, а вершины и звенья
ломаной в любой момент изменять.
Построение ломаной происходит в левой части
рабочего окна щелчками левой и правой кнопок
мыши:



щелчок левой кнопкой мыши на любом
звене ломаной добавляет новую вершину;
щелчок правой кнопкой мыши на любой
вершине удаляет вершину;
чтобы переместить любую вершину
ломаной достаточно зацепить ее левой
кнопкой мыши и, не отпуская кнопки,
перетащить на новое место.
Обратите внимание, что любые изменения
ломаной сразу отражаются на полученной
поверхности вращения.
Вращение построенной ломаной происходит
вокруг вертикальной оси Oy с помощью
специального "движка", задающего угол вращения.
Для изменения угла нужно зацепиться левой
кнопокой мыши за специальный "рычаг" и
повернуть его на нужный угол.
Текущее значение угла в градусах выводится в
строке статуса.
В правой части окна появляется поверхность или
тело, полученное в результате вращения ломаной.
Его можно перемещать и поворачивать в
пространстве:


левая кнопка мыши - зацепить за фон или
тело и перемещать его, не отпуская кнопки;
правая кнопка мыши - зацепить за фон или
тело и вращать его, не отпуская кнопки.
Включает и отключает режим, в котором вершины ломаной
"прилипают" к узлам целочисленной координатной сетки.
Увеличивает масштаб
Уменьшает масштаб
Позволяет выбрать один из шести основных видов
полученного тела: спереди, сзади, слева, справа, сверху, снизу.
Позволяет изменить настройки окна с изображением
трехмерного тела вращения:




рисовать или нет каркас;
закрашивать или нет полученную поверхность;
показывать или нет ось вращения;
изменить степень детализации изображения;

изменить использованные в изображении цвета.
Возвращает исходное задание
Позволяет открыть любой файл *.rot
Позволяет сохранить тело вращения в файле *.rot
Обращение к классу: «Сейчас вы разобьётесь по парам и займете место за
компьютером.
Далее
запустите
программу
«Геометрическое
конструирование». Щелкните по разделу Круглые тела. И последовательно
знакомясь с представленными моделями, выполняйте предложенные
упражнения и задачи. Если будут возникать затруднения обращайтесь ко
мне».
Также можно предложить учащимся на выбор построить такие
тела как: шахматные фигуры, стеклянная и глиняная посуда,
космические корабли, ракеты - всё, что нас окружает и может быть
получено путем вращения всего лишь одной кривой.
Сообщение о башне для радиостанции в Москве на
Шаболовке, построенной по проекту замечательного русского
инженера, почётного академика В. Г. Шухова. Она состоит из частей гиперболоидов вращения. Причём, каждый из них изготовлен из
прямолинейных металлических стержней, соединяющих соседние
окружности (рис.8, 9).
Задание на дом: сочинить вопросы о телах вращения, стихи или
кроссворды.