Вопрос 9. Новая теория инвестиций. Роль различных издержек регулирования капитала.

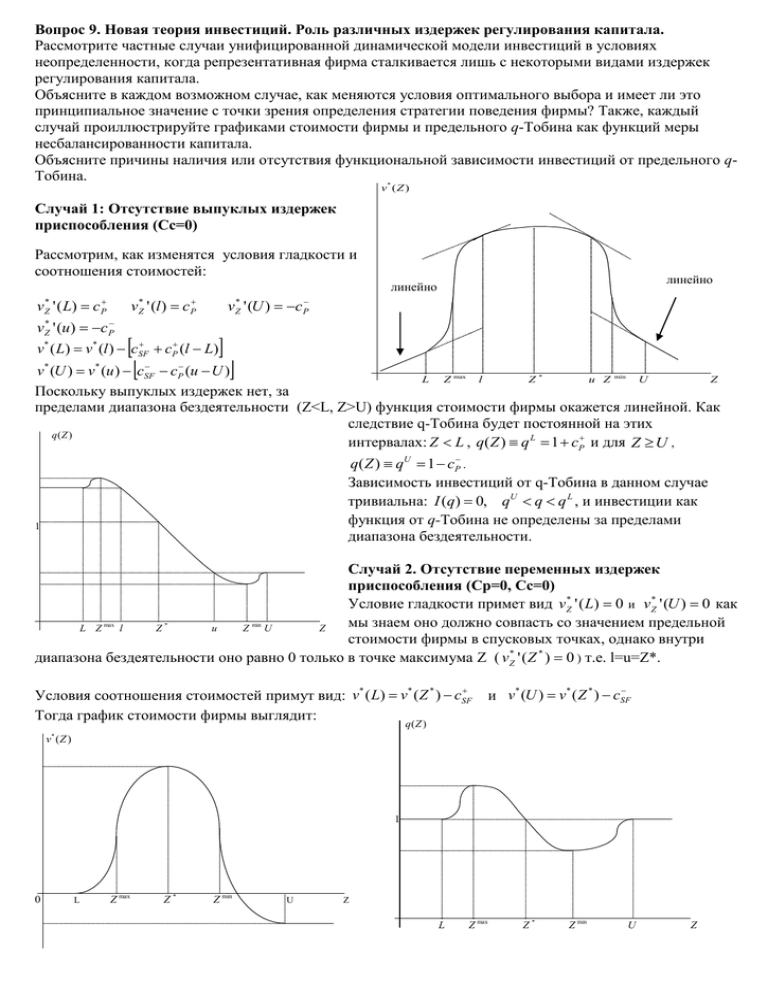
Вопрос 9. Новая теория инвестиций. Роль различных издержек регулирования капитала.
Рассмотрите частные случаи унифицированной динамической модели инвестиций в условиях
неопределенности, когда репрезентативная фирма сталкивается лишь с некоторыми видами издержек
регулирования капитала.
Объясните в каждом возможном случае, как меняются условия оптимального выбора и имеет ли это
принципиальное значение с точки зрения определения стратегии поведения фирмы? Также, каждый
случай проиллюстрируйте графиками стоимости фирмы и предельного q-Тобина как функций меры
несбалансированности капитала.
Объясните причины наличия или отсутствия функциональной зависимости инвестиций от предельного qТобина.
v* ( Z )
Случай 1: Отсутствие выпуклых издержек
приспособления (Сс=0)
Рассмотрим, как изменятся условия гладкости и
соотношения стоимостей:
линейно
линейно
vZ* ' ( L)  c P
vZ* ' (l )  c P
vZ* ' (U )  c P
vZ* ' (u)  c P

v* ( L)  v* (l )  cSF
 cP (l  L)





v* (U )  v* (u )  cSF
 cP (u  U )
L Z max l
Z*
u Z min U
Z
Поскольку выпуклых издержек нет, за
пределами диапазона бездеятельности (Z<L, Z>U) функция стоимости фирмы окажется линейной. Как
следствие q-Тобина будет постоянной на этих
q(Z )
интервалах: Z  L , q( Z )  q L  1  cP и для Z  U ,
q( Z )  qU  1  cP .
Зависимость инвестиций от q-Тобина в данном случае
тривиальна: I (q)  0, qU  q  q L , и инвестиции как
функция от q-Тобина не определены за пределами
диапазона бездеятельности.
1
Случай 2. Отсутствие переменных издержек
приспособления (Сp=0, Cc=0)
Условие гладкости примет вид v Z* ' ( L)  0 и vZ* ' (U )  0 как
мы знаем оно должно совпасть со значением предельной
L Z
l
Z
u
Z U
Z
стоимости фирмы в спусковых точках, однако внутри
диапазона бездеятельности оно равно 0 только в точке максимума Z ( v Z* ' ( Z * )  0 ) т.е. l=u=Z*.
max
*
min

Условия соотношения стоимостей примут вид: v* ( L)  v* ( Z * )  cSF
Тогда график стоимости фирмы выглядит:

и v* (U )  v* ( Z * )  cSF
q(Z )
v* ( Z )
1
0
L
Z max
Z*
Z min
U
Z
L
Z max
Z*
Z min
U
Z
Единственное, что можно сказать о зависимости инвестиций от предельного q-Тобина, это то, что в
промежутке от q( Z min ) до q( Z max ) , за исключением единичного значения, мы имеем однозначно
определенные нулевые инвестиции. В единице и других значениях предельного q-Тобина инвестиции не
определены.
Данный случай демонстрирует экстремальный пример сконцентрированных инвестиций – либо фирма не
инвестирует вовсе, либо инвестирует мгновенно и (возможно) много. (в точках L и U)
Случай 3. Отсутствие постоянных издержек приспособления (Сf=0)
Хотя постоянных издержек нет, наличие линейных переменных издержек приспособления означает, что
даже если принятие решений об инвестициях и не связано ни с какими фиксированными потерями,
существуют отличные от нуля предельные издержки. Значит предельный выигрыш от (бесконечно малых)
инвестиций должен покрывать эти предельные потери. Это означает, что диапазон бездеятельности и в
этом случае будет существовать. Только теперь границы диапазона, точки L и U будут служить не
спусковыми точками, а т.н. «отражательными барьерами» (reflecting barriers).
Условия гладкости принимают вид: vZ* ' ( L)  c P и vZ* ' (U )  c P .
При Z  L мы имеем vZ* ' ( L)  c P , для Z  U имеет место v Z* ' (U )  c P - это значит, что фирма
осуществляет инвестиции за пределами диапазона бездеятельности т.к. выгоды больше издержек и не
осуществляет внутри.
q(Z )
v* ( Z )
1
Z*
L
U
Z
L
Z*
U
Z
Инвестиции отрицательны и убывают со снижением q-Тобина для q  qU , равны нулю в диапазоне
qU  q  q L , и положительны и возрастают с ростом q-Тобина для q  q L .
I (q )
qU
1
qL
q
Случай 4. Отсутствие постоянных и выпуклых
издержек приспособления (Сf=0 Cc=0)
Случай качественно совпадает с предыдущим, однако изза отсутствия выпуклых издержек за пределами
диапазона бездеятельности функция стоимости фирмы
будет линейной. Аналогично q-Тобина будет
постоянной на следующих интервалах: для Z  L ,
q( Z )  q L  1  cP и для Z  U , q( Z )  qU  1  cP .
Зависимость инвестиций от qТобина является такой же
тривиальной, как и в случае
отсутствия только выпуклых
издержек приспособления,
рассмотренном выше: инвестиции
как функция от q-Тобина не
определены за пределами диапазона
бездеятельности, и только для
qU  q  q L мы имеем однозначную
характеристику I (q )  0 .
v* ( Z )
линейно
линейно
q(Z )
L
Z*
Z
U
Случай 5. Отсутствие постоянных и линейных
издержек приспособления. (Сf=0 Cp=0)
1
Фирма имеет дело только с «хорошо определенными»
выпуклыми издержками приспособления – все совпадает
с базовой неоклассической моделью инвестиций в
условиях определенности.
L
Z*
U
В качестве выводов из рассмотренных частных случаев ответьте на следующие вопросы.
В чем состоит природа отличий нечастых и сконцентрированных инвестиций?
И первые, и вторые определяются наличием диапазона бездеятельности, создающим для фирмы стимулы
отложить положительные или отрицательные инвестиции. Однако, нечастые инвестиции могут быть
предельно малыми, в случае когда диапазон бездеятельности определяется отражательными барьерами, с
другой стороны, когда диапазон бездеятельности представлен спусковыми точками и содержит целевые
точки, фирма заинтересована осуществлять лишь большие по объему инвестиции или дизинвестиции.
Что определяет существование стимула отложить инвестиции (существование диапазона
бездеятельности)?
Однозначно, за это не отвечают («хорошо определенные») выпуклые издержки приспособления.
Неверным было бы и утверждение, что решающую роль здесь играют постоянные издержки
приспособления. Рассмотренные выше примеры продемонстрировали нам, что диапазон бездеятельности
может появляться как в случае существования, так и в случае отсутствия постоянных издержек. Мы
можем сделать вывод, что как постоянные, так и линейные переменные издержки могут создавать стимул
откладывать инвестиции. Различие будет состоять только в том, что одни лишь линейные издержки
приспособления могут создать диапазон бездеятельности, построенный по принципу отражательного
барьера. Таким образом, наличие только переменных издержек приспособления не может объяснить
наблюдаемые в реальности сконцентрированные инвестиции. Для того чтобы последние имели место,
необходим диапазон бездеятельности со спусковыми и целевыми точками, т.е. необходимо наличие
постоянных издержек приспособления. Следует заметить, что наличие постоянных издержек создает
технологию приспособления с возрастающей отдачей от масштаба. И действительно, несложно понять,
что возрастающая отдача от масштаба в технологии приспособления – необходимая предпосылка для
существования сконцентрированных инвестиций.
В чем причина возможного нарушения «привычной» взаимосвязи инвестиций и предельного q-Тобина?
Наличие постоянных и (или) линейных издержек приспособления создает диапазон бездеятельности,
который может быть определен как в терминах меры несбалансированности капитала, так и в терминах
Z
предельного q-Тобина, и в котором инвестиции являются нулевыми. В отсутствии постоянных и
линейных издержек приспособления (т.е. в отсутствии диапазона бездеятельности) инвестиции равны
нулю только для одного значения предельного q-Тобина. За пределами диапазона бездеятельности
предельное q-Тобина будет принимать различные значения, и инвестиции будут функционально завесить
от предельного q-Тобина только в том случае, когда фирма имеет помимо прочих «хорошо
определенные» выпуклые издержки приспособления. Правда даже в этом случае, наличие постоянных
издержек приспособления может привести к возникновению интервалов справа и слева от диапазона
бездеятельности, где функциональная зависимость инвестиций от предельного q-Тобина не определена.
Какую роль играет фактор неопределенности в новой теории инвестиций?
Как рост неопределенности отразится на стимуле отложить инвестиции и на процессе накопления
капитала?
Изначально мы вводили стохастический процесс x(t), оказывающей воздействие на прибыль фирмы и, как
следствие, на желаемый запас капитала в каждый момент времени. В конечном итоге, неопределенность,
с которой сталкивалась фирма в нашем анализе, заключалась в стохастической динамике меры
несбалансированности капитала, т.е. в характеристике ее вариации.
Может ли рост неопределенности привести к появлению стимула отложить (положительные или
отрицательные) инвестиции? Нет. Как отмечалось выше, стимул отложить инвестиции просто означает
наличие диапазона бездеятельности. Но сам диапазон бездеятельности возникает вследствие
существования определенных издержек приспособления. И если, например, фирма оперирует только с
выпуклыми издержками приспособления, то даже в условиях неопределенности у нее не будет диапазона
бездеятельности и стимула откладывать инвестиции.
Может ли рост неопределенности усилить стимул отложить инвестиции? Да, если этот стимул
мог существовать и до этого, то есть если фирма имеет диапазон бездеятельности. Мы не рассматривали
формальное аналитическое решение модели, но интуитивно должно быть ясно, что большей вариации
стохастического процесса динамики меры несбалансированности капитала должен соответствовать более
широкий диапазон бездеятельности. А значит более сильным будет и стимул откладывать как
положительные, так и отрицательные инвестиции.
Можно ли утверждать, что в условиях большей неопределенности репрезентативная фирма
будет накапливать меньше капитала (например, из соображений предосторожности)? Однозначно
ответить на данный вопрос нельзя. В определенном смысле данный вопрос просто является
некорректным. И очевидно почему. Рост характеристики неопределенности в модели расширяет диапазон
бездеятельности и тем самым усиливает стимул откладывать как положительные, так и отрицательные
инвестиции. Другими словами, в «хорошие времена» фирма может иметь «слишком» низкий запас
капитала, т.к. существует более сильный стимул отложить положительные инвестиции, пока мера
несбалансированности капитала не приблизилась к
(отдалившейся) левой границе диапазона
бездеятельности. С другой стороны, в «плохие времена» фирма будет иметь «слишком» высокий запас
капитала по схожей причине. Так что правильным (и корректно сформулированным) утверждением
может быть следующее: рост неопределенности может привести к тому, что у фирмы будет наблюдаться
тенденция накапливать (иметь) «слишком» мало капитала в «хорошие времена», когда внешние факторы
увеличивают прибыль фирмы и требуют увеличить запас капитала, и напротив, в «плохие времена», когда
внешние факторы снижают прибыль и требуют снизить запас капитала, фирма будет часто
характеризоваться «слишком» высоким запасом капитала.
Имеет ли какое-нибудь отношение фактор неопределенности к возникновению проблемы полной
необратимости инвестиций? Нет, что очевидно из выше проведенных рассуждений.