Когда между катодом и анодом создается задерживающая

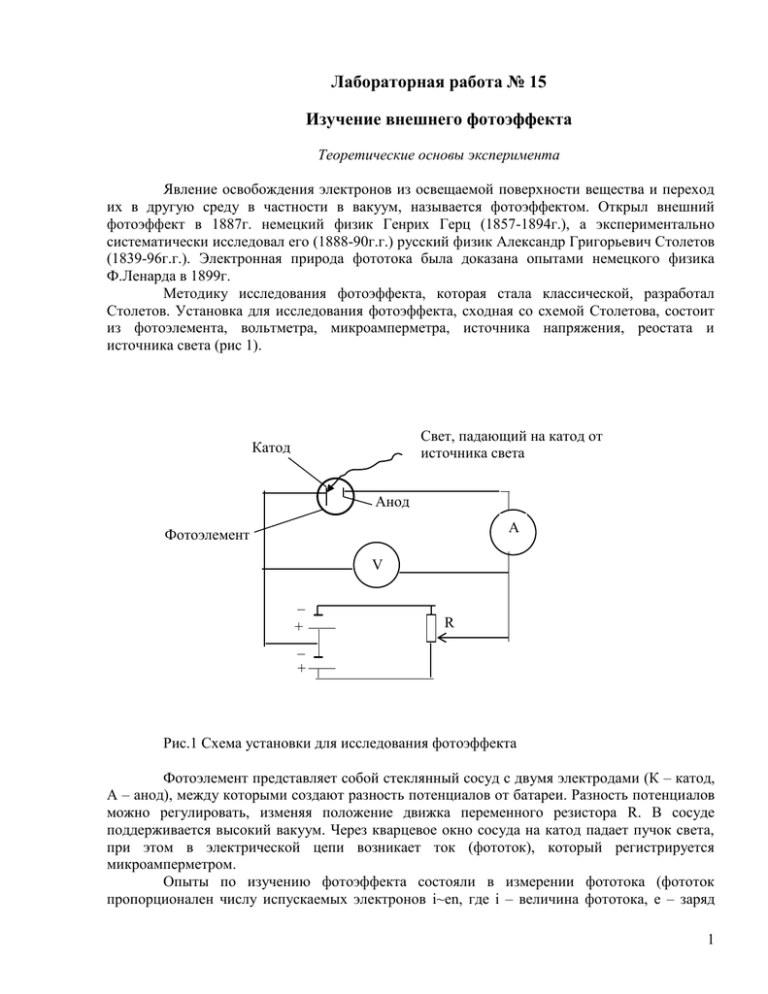
Лабораторная работа № 15
Изучение внешнего фотоэффекта
Теоретические основы эксперимента
Явление освобождения электронов из освещаемой поверхности вещества и переход
их в другую среду в частности в вакуум, называется фотоэффектом. Открыл внешний
фотоэффект в 1887г. немецкий физик Генрих Герц (1857-1894г.), а экспериментально
систематически исследовал его (1888-90г.г.) русский физик Александр Григорьевич Столетов
(1839-96г.г.). Электронная природа фототока была доказана опытами немецкого физика
Ф.Ленарда в 1899г.
Методику исследования фотоэффекта, которая стала классической, разработал
Столетов. Установка для исследования фотоэффекта, сходная со схемой Столетова, состоит
из фотоэлемента, вольтметра, микроамперметра, источника напряжения, реостата и
источника света (рис 1).
Свет, падающий на катод от
источника света
Катод
Анод
A
Фотоэлемент
V
_
+
_
+
R
Рис.1 Схема установки для исследования фотоэффекта
Фотоэлемент представляет собой стеклянный сосуд с двумя электродами (К – катод,
А – анод), между которыми создают разность потенциалов от батареи. Разность потенциалов
можно регулировать, изменяя положение движка переменного резистора R. В сосуде
поддерживается высокий вакуум. Через кварцевое окно сосуда на катод падает пучок света,
при этом в электрической цепи возникает ток (фототок), который регистрируется
микроамперметром.
Опыты по изучению фотоэффекта состояли в измерении фототока (фототок
пропорционален числу испускаемых электронов i~en, где i – величина фототока, e – заряд
1
электрона, n – число электронов) в зависимости от приложенной между анодом и катодом
разности потенциалов и изучения зависимости энергий электронов от интенсивности и
частоты падающего света. Разность потенциалов измерялась вольтметром.
Перечислим по порядку эксперименты, которые позволили выявить сущность
явления фотоэффекта.
1-ый эксперимент: катод фотоэлемента освещался светом постоянной интенсивности
и определенной частоты, а испускаемые электроны подвергались действию либо
ускоряющего, либо задерживающего электрического поля. Опыт показывает (рис.2), что при
нулевой разности потенциалов имеется поток электронов от катода к аноду. Увеличение
положительного потенциала на аноде (которое достигается передвижением ползунка
реостата вниз), ведет к увеличению фототока, так как возрастает ускоряющая сила,
действующая на электроны в электрическом поле. При определенной разности потенциалов
между анодом и катодом фототок достигает максимальной величины, называемой током
насыщения. Наоборот, задерживающее электрическое поле, когда положительный потенциал
больше у катода, чем у анода (при движении ползунка реостата вверх от центра), мешает
движению электронов от освещаемой поверхности к аноду. Фототок уменьшается и при
некоторой величине разности потенциалов, получившим название задерживающая разность
потенциалов, становится равным нулю.
.
I
0
Uзад
U
Рис.2 Зависимость фототока от разности потенциалов
Когда между катодом и анодом создается задерживающая разность потенциалов будут
задержаны даже электроны обладающие максимальной кинетической энергией, т. е.
mV 2
(1)
2
(где m – масса электрона, e – заряд электрона), фототок в цепи анода обратится в
нуль. Поэтому задерживающая разность потенциалов характеризует максимальную
кинетическую энергию, которую может иметь вылетевший под действием света электрон.
Проводя 2-ой эксперимент, будем изменять интенсивность L падающего света,
приближая источник света к фотоэлементу и, поддерживая частоту света постоянной.
eUзад=
2
Электрический
ток
L3=3L1
L2=2L1
L1
0
Разность потенциалов
U= -Uзад
Рис.3 Кривые фототока для трех значений интенсивности света L при постоянной
частоте  света
Опыт показал (рис.3), что сила тока насыщения прямо пропорциональна
интенсивности падающего света Iнас~ L .
Прямая пропорциональность силы фототока насыщения интенсивности света
свидетельствует, что число электронов, выбиваемых из катода в единицу времени,
пропорционально плотности светового потока или интенсивности света.
Замечательной особенностью результата (рис.3) является то, что задерживающая
разность потенциалов остается величиной постоянной независимо от интенсивности света.
В 3-ем эксперименте изменяли частоту падающего света при неизменной
интенсивности. На рис.4 представлены вольтамперные характеристики, полученные для
никеля. Кривые относятся к случаям освещения никелевого шарика светом трех различных
частот. Для всех трех кривых ток насыщения достигается при одной и той же разности
потенциалов U=+0,8 В. Эта величина представляет собой контактную разность потенциалов
между никелевым катодом и серебряным анодом. Вычитая эту величину (0,8В) из всех
показаний вольтметра, можно получить истинные значения задерживающих потенциалов.
Аналогичные кривые были получены для Al, Zn, Sn, Cd, Pb, Cu, Pt и Ag.
I
ν3>ν2>ν1
3
2
1
0
0,8
U,В
Рис.4 Кривые фототока для трех значений частоты света ν при постоянной
интенсивности света L, полученные для никелевого шарика (катода).
3
4-ый эксперимент (осуществленный американским физиком Робертом Милликеном
в 1916г.) заключался в установлении зависимости задерживающей разности потенциалов, а,
следовательно, и кинетической энергии вылетающих электронов от частоты падающего
света. Проведенные измерения показали (рис.5), что такая зависимость строго линейна
Uзад

0

кр
A
e
в ых
Рис.5 Зависимость задерживающей разности потенциалов Uзад от частоты света ν
С ростом частоты света ν задерживающая разность потенциалов (а значит и
максимальная энергия вылетевшего электрона) линейно возрастает. Результаты для разных
материалов катода приведены на рис.6.
Uзад
-U1
0

-U2
-U3
Рис.6. Зависимость Uзад от ν для трех катодов с различными значениями работы
выхода
Из рис.6 видно, что наклон прямых не зависит от вещества катода.
Таким образом, экспериментальные закономерности, выраженные графиками на
рис. 3-6, можно сформулировать в виде законов внешнего фотоэффекта:
при фиксированной частоте излучения число электронов, выбитых из катода в
единицу времени прямо пропорционально интенсивности света (плотности светового
потока энергии) (см. рис.3);
4
максимальная энергия фотоэлектронов не зависит от интенсивности светового
потока (см.рис.4 и (1) и линейно зависит от частоты света, падающего на катод
(см.рис.5);
для каждого металла существует красная граница фотоэффекта, то есть
минимальная частота света кр, при которой еще возможен фотоэффект (при
кр
фотоэффект невозможен).
Было предпринято также изучение времени запаздывания появления фототока
относительно начала облучения катода световым потоком. Какого-либо запаздывания
обнаружить не удалось.
В то время, когда был открыт фотоэффект, были изучены явления интерференции,
дифракции, поляризации света, которые хорошо объяснялись с помощью представления о
свете, как электромагнитной волне. Поэтому вначале были предприняты попытки объяснения
фотоэффекта с волновой точки зрения. Качественное объяснение на первый взгляд не
представляет трудностей.
Но, прежде всего, вспомним, определения электромагнитной волны и интенсивности
света, поскольку эти понятия использовались без точного определения.
Электромагнитная волна – это распространяющиеся в пространстве с конечной
скоростью (со скоростью света в вакууме -c) взаимосвязанные между собой переменные
электрическое и магнитное поля. В электромагнитной волне колеблются два вектора –
напряженности электрического E и напряженности H
магнитного полей. При
распространении электромагнитных волн происходит перенос энергии. Движение энергии в
электромагнитной волне изображается при помощи вектора S , который называется вектором
потока энергии. Впервые определение его было введено Джоном Пойнтингом (1852-1914г.г.).
Вектор S определяется как
c
E H
4
Модуль S равен интенсивности излучения (плотности потока энергии излучения),
который определяется как энергия, переносимая излучением в единицу времени через
единицу площади.
Интенсивность света пропорциональна квадрату амплитуды световой волны
S 
L  0  E2  c
(Как показывает опыт, мощность магнитного поля очень мала, поэтому
интенсивность света определяется через характеристику E – напряженности электрического
поля).
Возвращаясь к объяснению явления фотоэффекта с представления о свете, как волне,
можно представить, что падающая электромагнитная волна вызывает вынужденные
электромагнитные колебания электронов в металле; при резонансе между собственным
периодом колебания электрона и периодом падающей волны амплитуда колебаний электрона
становится настолько большой, что он может вырваться за пределы поверхности металла.
Чем больше интенсивность падающего света, тем большей кинетической энергией должен
был бы обладать электрон, покидающий металл, как бы заимствуя энергию у падающей
волны. На самом деле многочисленные опыты показали, что энергия фотоэлектронов
абсолютно не зависит от интенсивности света: повышение интенсивности увеличивает лишь
число фотоэлектронов, но не их скорость и, следовательно, энергию. В результате даже очень
5
слабый источник света может вызвать испускание электронов, обладающих большой
энергией, если частота света достаточно высока. Вместе с тем свет низкой частоты никогда
не вызывает испускания электронов, каким бы мощным ни был его источник. Эти результаты
никак не согласуются с теорией Максвелла, так как в соответствии с ней свет, или вектор
напряженности электрического поля передаёт свою энергию благодаря силе, действующей на
заряженный электрон со стороны электрического поля. Если источник слабый, то и вектор
напряженности электрического поля, распределенный по всему пространству, тоже будет
слабым. Для выбивания энергичного электрона такому слабому электрическому полю
потребуется много времени. На опыте же наблюдается практически мгновенное испускание
фотоэлектронов, как только свет, независимо от его интенсивности, попадает на катод.
Для объяснения явления фотоэффекта – освобождения электронов из вещества под
действием излучения, Альберт Эйнштейн в 1905г. предложил для своего времени
принципиально новую модель света и его взаимодействия с веществом. Эйнштейн
теоретически ввел понятие фотона (частицу света, которую называют также квантом света) и
рассматривал взаимодействие отдельного фотона с отдельным электроном.
Каждый фотон имеет энергию и импульс. Энергия фотона, соответствующая свету
частотой ν, равна
Е  h ,
(2)
импульс фотона равен
h
(3)
c
где h – постоянная Планка.
Фотон, столкнувшись с электроном в металле, передает ему свою энергию Е  h .
Если эта энергия достаточно велика, то электрон может преодолеть силы удерживающие его
в металле и выйти из металла.
Рассмотрим условия, в которых находятся электроны в металле. Согласно
классическим представлениям, в металле имеются свободные электроны, которые могут
обладать любыми значениями энергии. С точки зрения квантовой теории энергия электронов
в металле квантуется. Энергетический спектр электронов в металле имеет зонную структуру.
Каждая зона состоит из близко расположенных уровней. В основном, невозбужденном
состоянии атома суммарная энергия электронов имеет минимально возможное значение.
Поэтому, казалось бы, все электроны должны находиться на самом низком уровне. Однако
электроны подчиняются принципу Паули, который гласит, что в изолированной системе два
или более тождественных электрона не могут находиться в одинаковом состоянии. Если
представить себе вначале только решетку положительных ионов, внутрь которой вносятся
один за другим электроны при абсолютном нуле температуры (при этом энергия кристалла
должна быть минимальна), то первый электрон расположится на самом нижнем уровне,
второй электрон уже не сможет поместиться на этом уровне и должен будет расположиться
на следующем, более высоком и так далее. Потенциальных состояний в квантовой системе
(атоме, молекуле, кристалле) очень велико, наиболее высокие уровни будут от электронов
свободны. Самый верхний из этих уровней при абсолютном нуле образует резкую границу
между заполненными и незаполненными уровнями. Этот верхний уровень ЕФерми называется
границей Ферми и определяет максимальную энергию, которую может иметь электрон.
p
6
На рис. 7 представлены энергетические соотношения для электронов в зоне
проводимости металла.
Потенциа
льная
энергии
электрон
ов
Е
Металл
Max энергия
электронов внутри
металла
Вакуум
Е0
Авых
Еферми
Min энергия
электронов внутри
металла
Рис.7 Энергетические соотношения для электронов в зоне проводимости металла
По оси ординат отложены значения потенциальной энергии (уровни энергий)
электронов. Электроны в металле оказываются в электрическом поле кристаллической
решетки как бы заключенными в потенциальной яме, вырваться за пределы которой
самостоятельно они не могут. Эта яма на рис.7 представлена в виде жирной линии,
показывающей потенциальный барьер или значение потенциальной энергии Е 0, которой
обладают электроны внутри металла, определяет потенциальную энергию покоящегося
электрона вне металла (в вакууме). Очевидно, для освобождения электрона из металла ему
нужно сообщить энергию, по крайней мере, равную разности между глубиной потенциальной
ямы Е0 и энергией критического уровня Ферми ЕФерми(рис.7). Эта разность
Aвых  Е0  ЕФерм и
есть работа выхода электрона из металла Авых.
При фотоэффекте в процессе передачи электрону энергии фотона естественно
соблюдается закон сохранения энергии, который можно записать в виде:
mV 2
h  Aвых 
,
(4)
2
mV 2
где
- максимальная кинетическая энергия электрона непосредственно после
2
преодоления сил, удерживающих его в объеме металла, и выхода за пределы объема;
Авых – работа выхода (работа, совершенная электроном для преодоления сил,
удерживающих его в объеме металла).
7
Соотношение (4) называется уравнением Эйнштейна для фотоэффекта.
Уравнения (2),(3) и (4) полностью объясняют все особенности фотоэффекта.
Согласно квантовой теории света легко представить, что интенсивность света прямо
пропорциональна числу фотонов и энергии каждого из них. Каждый фотон поглощается
целиком только одним электроном. Поэтому число вырванных светом фотоэлектронов, а
стало быть, и фототок насыщения пропорционален числу фотонов, то есть интенсивности
света (первый закон фотоэффекта).
Следует отметить, что при фотоэффекте покинуть поверхность металла могут только
те электроны, которые обладают энергией близкой или равной энергии, соответствующей
уровню Ферми. Электроны, имеющие энергию, меньшую, чем ЕФерми, вообще не
испускаются.
Кинетическая энергия фотоэлектронов по уравнению (4) зависит только от энергии
фотона, выбившего электрон из катода, и не зависит от интенсивности падающего света
(второй закон фотоэффекта).
Из (4) также видно, что при энергии падающего фотона, меньшей работы выхода
электрона из металла фотоэффект невозможен. Этим объясняется наличие красной границы в
фотоэффекте (третий закон фотоэффекта).
Граничная частота νкр измеряется экспериментально, а работа выхода вычисляется с
помощью уравнения (4) при Vmax=0
А  h
вых
кр
(5)
или из графика рис.5, где отрезок, отсекаемый от оси потенциала (Uзад), дает
А
е
в ых
.
Работа выхода различна для различных металлов и составляет обычно несколько
электрон-вольт. Порог фотоэффекта для металлов с малой работой выхода (щелочные
металлы) лежит в видимой области спектра, а для металлов с большой работой выхода
(Ag,Ni,Pt) – в ультрафиолетовой области. Например, для Na красной границе соответствует
частота излучения или длина волны
c
ch
max 

 0,68 мкм
 кр Aвых
Такая длина волны находится в красном диапазоне видимого спектра, чем и
объясняется название красной границы.
Время запаздывания при фотоэффекте на основании изложенных представлений
равно времени движения электронов до поверхности металла после столкновения с фотоном,
то есть чрезвычайно мало и находится в согласии с экспериментом. Если бы фотоэффект
объяснялся постепенной «раскачкой» электронов электрическим полем волны, то время
запаздывания было бы чрезвычайно большим.
Р.Э.Милликен (1858-1953) провел (1914-1916) тщательные измерения фотоэффекта и
с большой точностью подтвердил справедливость уравнения (2). Уравнение (1) с учетом (4) и
(5) записываеися в виде
h
   кр ,
e
где е  1,6  10 19 Кл - элементарный заряд.
U зад 
8
Именно эта линейная зависимость U зад
от ν, показанная на рис.5, явилась
предметом исследований Милликена и использовалась им для определения h 
e U зад
   кр
.
Постоянную Планка можно определить по углу наклона  экспериментальной
прямой зависимости Uзад() (рис.5)
Было получено наиболее точное для того времени значение постоянной Планка
h  6,56  10 34 Дж  с
Важнейшее значение фотоэффекта в том, что его открытие и исследование стали
экспериментальным основанием квантовой теории.
На явлении фотоэффекта основано действие фотоэлементов, которые получили
большое распространение в технике. К ним относятся вакуумные фотоэлементы, практически
не обладающие инерционностью, и газонаполненные фотоэлементы, обладающие большой
инерционностью и большой чувствительностью. На рис. 8 показан внешний вид и схема
фотоэлемента, состоящего из стеклянной или кварцевой колбы, внутренняя часть которой
покрыта слоем светочувствительного металла -катод (используют щелочные металлы,
имеющие малую работу выхода Cs, Na, Zn, Ag, Pt).
Катод
Стеклянная колба
Анод
Цоколь
Рис.8 Внешний вид фотоэлемента.
Воздух из колбы тщательно удален. Внутри колбы имеется металлическое кольцо
(или сетка) - анод. Как от светочувствительного слоя, так и от кольца наружу сделаны
выводы, с помощью которых фотоэлемент присоединяется к батарее так, чтобы
металлический слой был катодом, а кольцо анодом. Свет, попадая на катод, выбивает из него
электроны, которые летят к аноду. В цепи идет фототок, обнаруживаемый
микроамперметром.
Чувствительность вакуумных фотоэлементов невелика, то есть ток в цепи
вакуумного фотоэлемента мал. Для усиления тока (повышения чувствительности) в колбу
вводят разреженный газ. В газонаполненных фотоэлементах электроны, вырываемые светом
из катода, при достаточном напряжении между катодом и анодом приобретают такую
скорость, что оказываются в состоянии ионизировать частицы газа, заполняющего
фотоэлемент; возникает ударная ионизация. Образовавшиеся при этом новые электроны, в
свою очередь, приходят в движение и ионизируют нейтральные частицы газа; в результате к
аноду устремляется все возрастающая лавина электронов, фототок значительно
увеличивается, чувствительность фотоэлемента растет.
9
Для образования носителей зарядов в газонаполненном фотоэлементе давление газа
должно быть таким, чтобы длина свободного пробега электрона в газе должна быть
достаточной, чтобы ионизировать молекулу газа. Действительно, в постоянном
электрическом поле напряженностью Е электрон, пройдя расстояние d, приобретет энергию
W=edE, которая зависит от расстояния d (при постоянных Е и е). Если атомов газа много (то
есть давление газа велико), то расстояние d между молекулами газа мало и электрон не
успеет при своем движении от катода к аноду приобрести достаточную для ионизации
энергию. Таким образом, при большом давлении хотя и наблюдается рост числа
столкновений электронов с молекулами газа, однако это не ведет к увеличению фототока.
Основное техническое применение фотоэлементы находят в фототелеграфии
(передачи изображения на расстояние по проводам), в телевидении и в звуковом кино. Кроме
того, фотоэлементы широко применяются в фотореле, с помощью которого автоматически
приводят в действие самые разнообразные механизмы.
Экспериментальная часть
Описание установки
A
УИП
ФЭ
V
Рис.9 Схема экспериментальной установки по изучению внешнего фотоэффекта
На рис 9. представлена схема экспериментальной установки по изучению внешнего
фотоэффекта. Вакуумный и газонаполненный фотоэлементы укреплены на подставке. Их
переключение осуществляется тумблером, находящимся на верхней крышке кожуха, который
прикрывает фотоэлементы. Электрическая лампа (осветитель) может передвигаться по
оптической скамье. Расстояние между осветителем и фотоэлементами измеряется с помощью
10
линейки. Последовательно с каждым фотоэлементом включены универсальный источник
питания УИП-1 и амперметр. Напряжение измеряется с помощью вольтметра.
Вопросы для допуска к работе
1. Какие элементы входят в состав установки? Каково их назначение?
2. Чему равна цена деления шкалы вольтметра и амперметра?
Примечание. Чтобы определить цену деления шкалы измерительного прибора, нужно
посмотреть на какой предел измерения физической величины установлен переключатель
диапазона измерения. Затем этот предел разделить на общее количество делений шкалы
прибора. Полученный результат от деления и будет равен цене деления. Например, если
переключатель диапазона измерений напряжения установлен на цифре 300В, а общее
количество делений на шкале вольтметра равно 30, то цена деления вольтметра будет равна
300В : 30 = 10В.
3. Как следует выполнять упражнение 1? До каких пор нужно увеличивать напряжение
между анодом и катодом при выполнении упражнения 1?
4. Как осуществляется переключение фотоэлементов с вакуумного на газонаполненный?
5. В чем отличие выполнения упражнения 2 от упражнения 1?
Практическая часть работы
Упражнение 1. Проверка закона Столетова.
1. Установить источник света на некотором расстоянии r1 от фотоэлементов и
включить его. Записать значение r1.
2. Включить вакуумный фотоэлемент тумблером на крышке корпуса
фотоэлементов.
3. С помощью ручки потенциометра изменять напряжение на зажимах
фотоэлемента с шагом 5В, записывать каждый раз значения силы тока по
показаниям микроамперметра. Если ток продолжает увеличиваться после того,
как стрелка вольтметра дошла до конца шкалы, нужно переключить указатель
диапазона изменения напряжения на другое значение, чтобы
изменять
напряжение с шагом 10В, также каждый раз записывая значение силы тока.
Изменять напряжение до тех пор, пока величина тока не будет оставаться
постоянной 3-4 раза.
4. Результаты измерений записать в таблицу №1.
5. Изменить расстояние от источника света до фотоэлемента в 2 раза, передвинув
осветитель вдоль скамьи.
6. Повторить действия п.п. 3,4 для расстояния r2. Записать значение r2.
7. Построить графики зависимости i от U для r1 и r2 на одной координатной
плоскости, откладывая по оси абсцисс величину напряжения, а по оси ординат
величину тока.
8. Сделать вывод о зависимости iнас от величины светового потока.
11
Таблица №1
r2(см)
r1(см)
U(В)
I(А)
U(В)
i(А)
1.
Упражнение2.Снятие вольтамперной характеристики газонаполненного
фотоэлемента.
Установить осветитель на определенном расстоянии r от фотоэлемента и
включить его.
Включить тумблером газонаполненный фотоэлемент.
Повторить измерения п.п. 3,4 упражнения 1(только для одного расстояния),
изменяя напряжение от 0 сразу с шагом 10В. (обратить внимание на то, что ток
насыщения в случае газонаполненного фотоэлемента не наблюдается).
Построить график зависимости i от U для данного расстояния r.
Сравнить вольтамперные характеристики вакуумного и газонаполненного
фотоэлементов.
2.
3.
4.
5.
Упражнение 3.Изучение зависимости фототока от освещенности поверхности катода
вакуумного фотоэлемента.
1.
Установить осветитель на возможно большом расстоянии r от фотоэлемента и
включить его.
2.
Включить тумблером вакуумный фотоэлемент.
3.
Вращая ручку источника питания УИП установить определенное значение
напряжения U, например, 50В.
4.
Записать величину силы тока i по показанию микроамперметра.
5.
Результаты измерений записать в таблицу №2.
6.
Приближая осветитель каждый раз на 10 см к фотоэлементу, записывать
значения силы тока по показанию амперметра и расстояния в таблицу №2
7.
Построить график зависимости фототока i от освещенности поверхности
фотокатода (освещенность E ~ 1/r2).
Таблица№2
U (В)
r(см)
1/r2
i(А)
12
Контрольные вопросы
1.
Что называется фотоэффектом?
2.
Рассказать об устройстве фотоэлемента, принципе его действия. Объяснить ход
кривых, полученных в результате выполнения упражнения 1. Какой ток называется током
насыщения и почему? Как по полученным результатам можно проверить выполнение
закона Столетова? Сформулировать первый закон фотоэффекта.
3.
Объяснить ход кривых упражнения 2. Что происходит при наполнении
фотоэлемента газом? Объяснить механизм ионизации газа.
4.
Какой из фотоэлементов обладает наибольшей чувствительностью и почему?
5.
Объяснить ход кривых в упражнении 3.
6.
Сформулировать второй и третий законы фотоэффекта.
7.
Что называется красной границей фотоэффекта?
8.
Какое уравнение называется уравнением Эйнштейна? Как называется величина
h в этом уравнении? Как по экспериментальным данным можно определить работу
выхода для данного металла?
9.
Какие затруднения возникли при объяснении фотоэффекта с позиций волновой
теории света?
10. Где применяется фотоэффект?
Список литературы
1. Бутиков Е.И. “Оптика”, М.,”Высшая школа”,1986г.
2. Матвеев А.Н. “Атомная физика”, М.,”Высшая школа”,1989г.
3. Шпольский Э.В. “Атомная физика” Л.,Гос.изд-во технико-теоретической лит-ры,
1950г.
4. Спроул Р. “Современная физика”, М. ГИФМЛ, 1961г.
5. Купер Л. “Физика для всех. Современная физика”, М. Изд-во Мир, 1974г.
13
САМАРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
Кафедра общей и теоретической физики
ОПТИКА
Лабораторная работа №15
Изучение внешнего фотоэффекта
14