На правах рукописи Ко Ко Зо
реклама

На правах рукописи
Ко Ко Зо
ПРОЦЕССЫ РЕГУЛИРОВАНИЯ ТЯГОВОГО ЭЛЕКТРОДВИГАТЕЛЯ
ПРИ ПИТАНИИ ОТ ИМПУЛЬСНОГО ПРЕОБРАЗОВАТЕЛЯ
Специальность 05.09.03 – Электротехнические комплексы и системы
АВТОРЕФЕРАТ
диссертации на соискание учёной степени
кандидата технических наук
Москва 2010
Работа выполнена в Государственном образовательном учреждении
высшего профессионального образования «Московский государственный
университет путей сообщения» (МИИТ) на кафедре «Электрическая тяга»
Научный руководитель
– доктор технических наук, профессор
Феоктистов Валерий Павлович
(МИИТ)
Официальные оппоненты – доктор технических наук, профессор
Сидоренко Валентина Геннадьевна (МИИТ)
– кандидат технических наук,
Чернов Олег Евгеньевич (ОАО «РЖД»)
Ведущее предприятие
– ВИНИТИ РАН
Защита диссертации состоится « 03 » июня
2010 г. в 1500 час. на
заседании диссертационного совета Д 218.005.02 в Московском
государственном университете путей сообщения (МИИТ) по адресу: 127994,
г.Москва, ул. Образцова, д. 9, стр.9, аудитория 4210 .
С диссертацией можно ознакомиться в библиотеке унирвеситета.
Автореферат разослан « 29 »
апреля
2010 г.
Отзывы на автореферат в двух экземплярах, заверенные гербовой печатью
учреждения, просим направлять по адресу диссертационного совета
университета.
Учёный секретарь диссертационного совета Д 218.005.02
доктор технических наук, ст. науч. сотрудник
2
Н.Н. Сидорова
ОБЩАЯ ХАРАКТЕРИСТИКА РАБОТЫ
Актуальность работы заключается в необходимости разработки
комплексной методики расчета и моделирования систем импульсного
безреостатного регулирования тяговых электродвигателей ТЭД. Эта задача
особенно актуальна при выполнении системы управления и регулирования
соответствующего тягового электропривода на базе цифрового принципа
регулирования. Несмотря на достаточно хорошую проработанность цифровых и
импульсных систем в классической теоретической технической литературе
необходимо уточнение соответствующей теории конкретно применительно к
тяговым электроприводам с импульсным регулированием.
Целью работы является уточнение закономерностей электромагнитных
процессов, возникающих в тяговом электроприводе вследствие дискретности
импульсного преобразователя при постоянной рабочей частоте и из-за
особенностей микропроцессоров и дискретности цифрового регулятора. Целью
данного исследования является разработка рекомендаций по исключению
мешающего влияния тока ТЭД автоколебаний на системы железнодорожной
автоматики.
Методика исследований включает решение дифференциальных
уравнений электромагнитных процессов с их последующей алгебраизацией и
сведением к системе линейных уравнений. Для исследования квазислучайных
автоколебаний использован метод фазовой плоскости с линеаризацией фазовых
траекторий системы в пределах промежутков между линиями переключения
регулятора.
Научная новизна работы. Уточнен метод расчета частотных и
амплитудных параметров квазистационарных автоколебаний тока тягового
электродвигателя в замкнутом контуре регулирования с обратной связью по
отклонению, а также уточнена методика их поэтапного расчета. Выделены
стационарная и случайная составляющие периода и амплитуды автоколебаний
при компьютерном моделировании процесса регулирования с использованием
метода фазовой плоскости.
В результате поэтапного расчета этих
автоколебаний уточнены условия и причины их возникновения, а также
рекомендованы возможности обеспечения электромагнитной совместимости
тягового электропривода с системами ж.-д. автоматики.
Пратическая ценность исследования состоит в том, что уточнены
статистические распределения параметров квазипериодических автоколебаний
тока тяговых электродвигателей, что может быть использовано при анализе и
обеспечении электромагнитной совместимости тягового электропривода с
устройствами железнодорожной автоматики.
Достоверность полученных результатов подверждается корректностью
использования классических методов расчета импульсных нелинейных систем
3
и совпадением теоретических результатов с обобщенными результатами
компьютерного моделирования в переделах расхождения, допустимого в
инженерных расчетах .
Апробация работы. Основные положения работы докладывались на
научно-технических конференциях «Безопасность движения поездов»,
проводимых в Московском государственном университете путей сообщения
(МИИТ) в 2007-2009 гг.
Публикации. По теме диссертационной работы имеется 5 публикаций, из
них одна публикация в издании, рекомендуемом ВАК.
Объем работы. Диссертационная работа состоит из введения, пяти глав и
общих выводов по результатам работы, списка используемой литературы,
содержит 114 страниц текста, 36 рисунков, 4 таблиц.
СОДЕРЖАНИЕ РАБОТЫ
Во введении обоснована актуальность проблемы безреостатного
регулирования тяговых электродвигателей мотор-вагонного электроподвижного
состава постоянного тока. Приведены соответствующие данные по
энергозатратам и потерям электроэнергии (табл. 1). Даны ссылки на ранее
выполненные исследования и на конкретные научные практические разработки
по городскому и пригородному электротранспорту, с питанием от контактной
сети постоянного тока.
Таблица 1 – Обобщенные данные по параметрам движения и затратам энергии
пригородного и городского электротранспорта в Москве
Вид
электрического
транспорта
Среднее
расстояние
между
остановками, км
Удельные
энергозатраты,
Вт-ч/т-км
Доля пусковых и
тормозных
потерь
электроэнергии,
%
Пригородные
электропоезда
5,4
28
24
Метро
1,5
41
33
Трамвай,
Троллейбус
0,36
72
39
4
Первая глава содержит аналитический обзор по тяговым электроприводам
электропоездов постоянного тока. Возможности современной электронной
преобразовательной техники позволяют перейти на бесколлекторные двигатели,
что отражено в табл. 2. Однако с учетом того, что весь эксплуатируемый парк
электропоездов имеет ТЭД постоянного тока последовательного возбуждении,
обоснована целесообразность варианта 1.2 с модернизацией экспуатируемых
электропоездов с реостатным регулированием (вариант 1.1). Системы
безреостатного импульсного регулирования достаточно хорошо отработаны.
Имеется возможность использовать силовые транзисторы IGBT, что позволит
повысить рабочую частоту преобразователя до 2-3 кГц.
Таблица 2 – Мотор-вагонный ЭПС постоянного тока
Классификация мотор-вагонного ЭПС
2.2. Однозвенной
преобразователь АИН(ШИП)
2.1. Двухзвенной
преобразователь ШИП+АИН
1.2. Импульсное
регулирование ТЭД
1.1. Реостатный пуск
ТЭД
1. ЭПС с коллекторными
2. ЭПС с
ТЭД
бесколлекторными ТЭД
Для обоснования математической модели с целью последующего расчета
электромагнитных процессов импульсного регулирования рассмотрена схема
замещения ТЭД. Для этого проанализированы классические схемы замещения
электродвигателя постоянного тока, которые предложили д.т.н. Жиц М.З. и
д.т.н. Ранькис И.Я. Первая из них наиболее приспособлена для расчета
переходных процессов. Вторая разработана и детально исследована для
квазистационарного установившегося процесса импульсного регулирования. В
своей монографии д.т.н. Ранькис И.Я. (по этой монографии он защитил
докторскую диссертацию) делает вывод, что при высоких частотах импульсного
регулирования целесообразно упростить классическую схему замещения ТЭД с
учетом размагничивающего эффекта вихревых токов. И рекомендует сделать
5
это
путем
соответствующего
снижения
индуктивности
основного
намагничивающего контура. Это справедливо для стабилизированной рабочей
частоты – отклонения не более
±1%, что обеспечивается кварцевым
генератором импульсов в ситеме управления преобразователя.
Силовая часть тягового электропривода с импульсным преобразователем
хорошо вписывается в типовую двухконтурную систему автоматического
регулирования ТЭД (рис. 1, а). Здесь импульсный преобразователь представлен
звеном ИЭ, а ТЭД условно разделен на электрическую и электромеханическую
компоненты ТД1-ТД2. Алгоритм регулирования тока и скорости поезда в этой
системе показан на рис. 1,б. Пример расчета переходных процессов
регулирования тока приведен на рис. 1, в для ТЭД типа УРТ-110 при разных
значениях коэффициента усиления звена УЭ; переходной режим соответствует
этапу 1-2 по рис. 1, б. Материал главы 1 посвящен классическому подходу к
анализу непрерывных систем авторегулирования.
а)
U
Iм
ЭC1
Vз
ΔV
ЭC2
ЗТ
Iз
Инэ
ΔI
IЗ*
γ
УЭ
ИЭ
Uн
ТД1
I
V
ΣW
ТЭД
I
ТД2
F
V
М
OC1
OC2
V
е
б)
в)
I, A
ΔV∞
VЗ=21м/с
i=2,5‰
200
Vз
ΔVe
2
150
1
е
15
100
20
32 25
40
50
k=60
0
Iтр
I0
Iз
t, c
I
0
5
10
15
20
25
30
Рис. 1. Двухконтурная система авторегулирования
На этой основе в диссертации сформулирована задача уточнения
классической методики применительно к дискретности импульсного
преобразователя, работающего со стабилизированной частотой, и к
6
особенностям цифрового регулятора, в частности малоразрядного бортового
микропроцессора.
Вторая глава посвящена расчету электромагнитных процессов в системе
импульсного регулирования ТЭД. При этом показано, что изменение тока в
контуре регулирования в течение каждого из характерных промежутков
импульсного цикла преобразователя (ВКЛ. – ВЫКЛ.) подчиняется
экспоненциальному закону в функции времени. На этой основе выполнены
расчетные модели в диссертациях д. т. н. Некрасова В.И. и к.т. н. Чаусова О. Г.
Но для высоких частот импульсного преобразователя (400 Гц и выше), когда
пульсации тока нагрузки ТЭД не превышают 7%, то для инженерных расчетов
можно принять допущение о линейности изменения тока в функции времени в
течение каждого характерного интервала в период импульсного регулирования
(допущение №1). Исходная расчетная схема дана на рис. 2, а; указанное выше
допущение 1 показано на рис. 2, б.
В результате решения алгебраизированной системы по табл. 3 при
введении допущения №2 (е ≈ Е) имеем выражения для амплитуды пульсаций и
среднего значения тока
U
(1)
I k (1 k )
lf
I
Uk E
r
(2)
Из условия экстремума для (1), которое имеет вид
d (I ) U
(1 2k ) 0
dk
lf
(3)
получаем выражение для максимума пульсаций тока
I max
U UT
4lf
4l
(4)
Относительная пульсация тока ТЭД по отношению к его среднему
значению в процентах равна.
I 100UT
(5)
I * 100
k (1 k ), %
I
Il
Абсолютные и относительные значения пульсаций тока для двигателя УРТ110 во всем диапазоне регулирования k представлены на рис. 2, в.
Лимитирующим является режим с ΔI= ΔImax, что имеет место при k = 0,5.
Поэтому все расчеты для условий коммутации на коллекторе ТЭД и для
пульсационных потерь в ТЭД следует вести для данного режима. В гл. 2
рассчитана пульсационная компонента процесса импульсного регулирования,
которая имеет строго постоянную частоту. Но в сочетании с цифровым
регулятором эта картина качественно меняется. В работах процессоров Ту Ю,
Зайцева А. В., Колоколова Ю. В., Феоктистова В. П. и Жусубалиева Г. А.
7
показано, что при наличии цифрового регулятора возникает ряд явлений,
которые можно отнести к теории бифуркационных процессов. Именно в этом
направлении развито исследование в последующих главах диссертации.
Соответствующий эффект проявляется прежде всего в появлении
квазислучайных автоколебаний тока в обмотках ТЭД и соответственно в
рельсовых цепях.
а)
б)
ИП
i
+
i
I
ИП ВЫКЛ. ИП ВКЛ.
i
I
\
r
f, k
U
ИП ВКЛ.
l
ОД
kT
е
T
(1- k)T
t
в)
ΔI, A
ΔI*
ΔI*, %
14
25
ΔI
20
12
10
8
15
6
10
4
5
2
0
0,5
1
k
Рис. 2. Система импульсного регулирования (а), допущения (б)
и зависимости (в) пульсаций
Третья глава посвящена анализу структуры цифровых регуляторов для
тяговых электроприводов и обоснованию метода расчета квазистационарных
процессов при цифровом управлении импульсным преобразователем. Цифровой
регулятор должен соответствовать классической схеме, характерной для
8
электроприводов со стабилизацией основных параметров, т. е по классическому
принципу пропорциально-интегрального регулятора, что соответствует
внутреннему контуру регулирования с обратной связью ОС1 (рис. 1, а).
Практическая реализация этого контура целесообразна на базе малоразрядного
бортового микропроцессора МП (рис. 3) с выходным регистром Вых. Рг и с
входным элементом сравнения ЭС. В цепи обратной связи ОС включены
чувствительный элемент ЧЭ и дискриминатор уровня ДУ с зоной
нечувствительности ± δ, который выполняет функции аналого-цифрового
преобразователя АЦП. Современные микропроцессоры позволяют реализовать в
одном функциональном блоке микропроцессора все указанные выше элементы,
обеспечивая стабилизацию тока объекта регулирования ОР (ТЭД).
Рассмотрены и проанализированы также и другие варианты возможных
структур цифровых регуляторов с регулированием как по отклонению, так
дополнительно и по возмущению. С учетом этого предложена обобщенная
математическая модель, позволяющая учесть дискретность импульсного
преобразователя со стабилизованной частотой f=1/T и дискретность цифрового
регулятора. При этом выделены этапы развития этой модели (табл. 4), что
позволило уточнить ряд малоисследованных эффектов, в частности условия
возникновения и параметры квазислучайных автоколебаний. Эффект от
дискретности импульсного преобразователя рассмотрен ранее (см. рис. 2). Далее
методом наложения (принцип аддитивности) рассмотрено влияние системы
цифрового регулирования. При этом предварительно сформулировано условие,
согласно которому для решения задачи этапа 4 пульсации тока от импульсного
преобразователя пренебрежимо малы (ΔI ≈ 0). Отдельно нужно отметить, что
пульсации от ИП исследованы на этапе 3.
Это позволяет на этапе 4 выделить и исследовать только
квазистационарные автоколебания, возникающие из-за задержки управляющего
сигнала в регуляторе. Амплитудно-временные параметры этих автоколебаний
рассчитаны на основе классического метода фазовой плоскости в сочетании с
методом статистического моделирования. В целях приближения расчетной
методики к практике инженерных расчетов целесообразно линеаризовать
фазовые
характеристики
ОР
на
базе
2-точечного
приближения.
Соответствующая ошибка незначительно из-за малой величины зоны
нечувствительности релейных элементов в регуляторе.
9
Микропроцессор
Iз
ЗЭ
ИЗв
Вых. Рг
ДУ
ЧЭ
m
i
ОР
i*
Рис. 3. Характерная структура цифрового регулятора для тягового привода с
использованием микропроцессора
Таблица 4 – Этапы исследования автоколебаний при цифровом регулировании
импульсного преобразователя для ТЭД
1
Формирование условия наличия или отсутствия
автоколебаний
2
Расчет параметров автоколебаний (амплитуда и
частота для идеального регулятора (τ = 0))
Расчет параметров автоколебаний с учетом
дискретноти силовой части импульсного
преобразователя ИП (f; k)
3
Параметры автоколебаний при учете неидеальности
цифрового регулятора (τ > 0)
4
p
0
5
τmax τ
лог.нормальное
нормальное
равномерное
p
p
0
τmin τmax τ
0
Совместный учет случайных факторов влияния
от ИП и цифрового регулятора
10
τ
В соответствии с этим фазовые траектории ТЭД при цифровом
регулировании для его схемы замещения, содержащей активное сопротивление
R, эквивалентную индуктивность L* и противо-ЭДС e=cnФ , для каждого
значения выходного двоичного кода m (рис. 3) микропроцессора могут быть
записаны как
dI U kmax kmin
R cn
(6)
yт
ту ,
dtт L
2N 1
LI
L
Причем для дальнейшего анализа использована аппроксимация кривой
намагничивания двигателя. Поскольку рассматриваются автоколебательные
процессы с небольшими пульсациями тока, то фазовые траектории могут быть в
окрестности точек их пересечения с осью абсцисс (ось тока) заменены
касательными к реальным фазовым траекториям. Из этого допущения при уm=0
получаем возможность перейти к линеаризированным фазовым траекториям, т.
е. имеем прямые
d dI m
(7)
Yт ( I m0 I )
dI m0 dt
Их положения рассмотрены по отношению к вертикальным линиям
переключения в системе авторегулирования
i I з ;
i I з ;
(8)
они полностью определяют квазистационарный режим функционирования всей
системы. Таким образом, положение фазовых траекторий определяется
разрядностью цифровой системы и параметрами тягового двигателя, а также
уставкой I3 и зоной нечувствительности 2 дискриминатора уровня ДУ на рис.
3. Следовательно, параметры автоколебательного режима в конечном итоге
зависят от особенностей выполнения цифрового регулятора и от параметров
объекта регулирования. Для упрощения решения задачи ее целесообразно
разбить на этапы, решаемые последовательно, и показанны в табл. 4.
Условия возникновения автоколебаний могут быть сформулированы
следующим образом: если в промежутке между линиями переключения всегда
имеется хотя бы одна точка пересечения фазовой траектории с осью абсцисс,
как показано на рис. 4, а, то автоколебаний нет. При этом система работает с
рассогласованием (статической ошибкой) i, равномерно распределенной в
интервале от – до +.
11
а)
yт-1
yт
-δ
di
dt
б)
yт-1
yт+1 yт+2
δ
0
yт+1
di
dt
(i-Iз)
-δ
0
δ
(i-Iз)
г)
в)
yт
yт
1
1,0
0,5
p(N′y)
p(N y)
p(1)
p(2)
p(3)
2
p(1)
1
0
-δ
δ (i-Iз)
0
yт+1
p(3)
p(2)
p(0)
p(4)
2δ/Δ
2
3
4
2
3
4
д)
p(N′y)
1,0
p(N y)
p(0)
4
0,5
p(1)
3
0
Δ/2δ
1
Рис. 4. Автоколебания в тяговом электроприводе с цифровым регулятором:
а) автоколебания невозможны ; б) автоколебания возможны; в) фазовый потрет
автоколебаний; г, д) вероятностные зависимости для условий появления
автоколебаний
Таким образом, условие работы системы без автоколебаний может быть
сформулировано как
I т0 (iт0 i( ту 1) ) 2
(9)
В противном случае, т.е. при Δim0 > 2δ, возможно два варианта в
зависимости от взаимного положения фазовых траекторий и линий
переключения. Если между линиями переключения окажется одна точка im0
(рис. 4, б), то система работает без автоколебаний с рассогласованием
( I з iт0 )
(10)
Если при изменении каких-либо параметров тягового электропривода (n, I3,
U и т.д.) точка im0 выйдет за пределы промежутка между линиями переключения
12
(рис. 4, в), то квазистационарный режим системы будет характеризоваться
устойчивыми автоколебаниями с фазовым портретом ромб 1234. Он включает в
себя отрезки двух соседних фазовых траекторий, а также пересекающие их и
заключенные между ними отрезки линий переключения. Таким образом,
необходимое и достаточное условие автоколебаний может быть
сформулировано как отсутствие точек пересечения фазовых траекторий с осью
абсцисс в промежутке между линиями переключения.
Эти понятия могут быть уточнены за счет введения в рассмотрение
количества возможных состояний устойчивого равновесия системы Ny, которое
равно числу точек пересечения фазовых траекторий с осью абсцисс в
промежутке между соседними линиями переключения. Из сформулированных
выше условий и геометрических соотношений на фазовой плоскости следует,
что
(11)
N y 2 (im ) 2 (im ) 1 ,
где – символ дизъюнкции;
{ } – целое число после отбрасываниея дробной части у выражения в скобках.
Это выражение имеет вероятностный характер, поскольку возможны два
количественных показателя, характеризующих число состояний устойчивого
равновесного состояния системы, отличающиеся друг от друга на единицу. Эти
показатели условно обозначим
(12)
N y 2 (im ) ; N y N y 1
Вероятность того, что будем иметь Ny состояний равновесия, равна
p( N y ) 1 2 (im ) 2 (im ) ,
(13)
а вероятность наличия Ny состояний равна
p( N y ) 2 (im ) 2 (im ) ,
(14)
причем эти соотношения более наглядно представлены в виде графиков на рис.
4, г, где в качестве аргумента взято соотношение 2/im0. Если в качестве
аргумента принять обратное соотношение, то соответствующие графики будут
иметь не линейный, а экспоненциальный характер (рис. 4, д).
В случае автоколебаний (фазовый портрет которых определяется ромбом
1234 на рис. 4, в.) их параметры (этап 2) существенно зависят от ориентации
указанного ромба по отношению к оси абсцисс, а точнее от смещения по
вертикали его геометрического центра 0. При этом период автоколебаний Т
зависит от взаимного положения фазовых траекторий Ym и Ym+1 и линий
переключения по формуле
13
T ln
(Imoi I з )(I moi 1 I з )
(Imoi I з )(Imoi1 I з )
Соответственно
Tmin ln
(15)
1 (2 I m 0 )
1 (2 I m 0 )
(16)
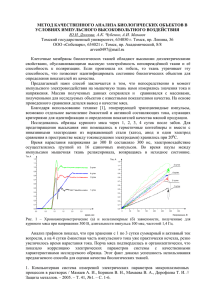
Эта зависимость Т(Y) показана на рис. 5, a, б, в и имеет характерную
параболическую форму с двумя асимптотами.
б)
а)
yт+1
ΔY
0,75 0,5
Т,с
(i-Iз)
0,6
0
yт
0,4
2
0 ,5
T0
Т
0,2
-ΔYmin
0
ΔY
TAmin
ΔYmax
0
0,25
0,50
1,00
0,75
г)
в)
p(T)
1
p
1
0
Tmin
T∞
д)
p(f)
2
T0
f
0
fmax
Рис. 5. Частотные характеристики автоколебаний в тяговом электроприводе с
двигателями УРТ-110 и с идеальным цифровым регулятором
14
Таким образом, в случае идеального цифрового регулятора ( = 0)
амплитуда автоколебаний равна
А=2, а период также определяется
детерминированной зависимостью (15). Однако, эта зависимость является
детерминированной только для заданного положения фазовых траекторий и
линий переключения. Поскольку в произвольный момент времени взаимная
ориентация фазовых траекторий и линий переключения может быть любой, то
смещение Y может рассматриваться как случайная величина с равномерным
распределением.
Поэтому даже при идеальном цифровом регуляторе функционирование
системы в целом описывается вероятностными соотношениями двух видов: 1)
вероятность появления или отсутствия автоколебаний; 2) временные и
амплитудные параметры этих автоколебаний (рис 5, г, д,).
В четвертой главе показано, что автоколебательный режим целесообразно
описать на основе вероятностно-статистических методов. Если через p(1)
обозначить вероятность наличия автоколебаний, а через p(0) – вероятность
стационарного режима без автоколебаний, причем p(1)=1–p(0), то
соответствующие зависимости имеют вид, как показано на рис. 4, д, в функции
отношения расстояния Δ между фазовыми траекториями к расстоянию 2δ между
линиями переключения. Если в качестве аргумента взять обратную величину
2δ/Δ , то эти зависимости будут линейными. Аналогичным образом
вероятностные соотношения могут быть использованы и для оценки периода
автоколебаний. Если геометрический центр ромбического фазового портрета
находится на оси абсцисс, то период автоколебаний равен Tmin < T < Tmin + 2/fги а,
соответствующее статическое распределение для периодов получатся
равномерным (рис. 6, а) в пределах < T < Tmin + 2/fги.
В общем же случае для обеих рассматриваемых систем фазовый портрет
может быть произвольно ориентирован по высоте относительно оси абсцисс,
что соответствует равномерному распределению вероятностей дл периода Tmin <
T < ∞ (рис. 6, б)
Если взять частоту автоколебаний, т. е. f =1/T,то ее максимальные значения
будут однозначно определяться параметром системы 2δ/Δ (рис. 6, в), а
распределение ее значений в пределах 0 < f < fmax режима является также
амплитуда А изменения тока двигателя. Практическое использование
рассмотренной методики сводится к тому, что в процессе проектирования
цифровой системы управления для тяговых электроприводов определяем
граничные значения параметров автоколебательного режима и соответствующие
им вероятностные распределения. Далее проводим проверку рассчитанных
параметров по отношению к границам зон запрещенных частот. Это связано с
функционированием устройств железнодорожной автоматики и связи, а также с
15
явлением резонанса во входных фильтрах преобразователей. Такая проверка
цифровой системы должна проводиться обязательно на стадии ее
проектирования. Эти расчеты выполнены для цифровой системы управления
импульсного преобразователя ТИП-1320/3 ТЭД типа УРТ-110. В процессе
расчетов параметры системы подобраны так, чтобы частоты автоколебаний не
превышали 19 Гц. Расчетные значения частот, амплитуд и вероятностных
характеристик совпали с опытными значениями, которые были зафиксированы
при поездных испытаниях преобразователя.
а)
p(T)
T
0
Tmin
б)
Tmin
2
f
в)
f
p(T)
0
0
г)
p(A)
p(1)
∞
Tmin
1
д)
p(A)
p(1)
1-p(1)
1 p (1)
2
0
2δ
2
A
0
2δ
A
2δ+2Δ
Рис. 6. Вероятностные характеристики цифровой системы автоматического
регулирования:
а, б – для периода Т; в – для частоты f; г, д – для амплитуды А
16
Выше рассмотрен процесс дискретного (цифрового) регулирования тока с
изображением на фазовой плоскости только гладкой составляющей
регулируемой величины, т.е. без учета пульсаций на рабочей частоте
импульсного
преобразователя.
При
учете
импульсного
характера
исполнительного элемента результирующий фазовый портрет существенно
меняется. Однако, если для гладкой составляющей приходится рассматривать
довольно много фазовых траекторий, количество которых соответствует числу
позиций выходного регистра или счетчика в цифровом регуляторе, то с учетом
пульсирующей составляющей независимо от цифрового регулятора
изображающая точка может находиться только на одной из двух траекторий.
Изображающая точка при этом перемещается по фазовым траекториям, которые
описываются уравнениями соответственно для включенного и выключенного
состояний исполнительного элемента
y1 1 L U E (i ) Ri ;
(17)
y0 1 L E (i ) Ri ,
а моменты перехода с одной траектории на другую и обратно определяются
значением коэффициента заполнения k, задаваемым цифровым регулятором, а
также рабочей частотой f импульсного преобразователя. Фазовый портрет
представляет собой прямоуголные петли, причем среднее за период пульсации
смещение изображающей точки в направлении оси абсцисс соответствует ее
смещению по параллелограмму 1234.
Из-за того, что моменты переключения задающего генератора и
импульсного преобразователя и моменты изменения кода в цифровом
регуляторе не могут быть синхронизированы между собой, имеет место
“расплывание” фазового портрета для гладкой составляющей, как показано
штриховкой. В целях упрощения расчетной процедуры целесообразно оценить
возможное увеличение амплитуды и периода колебаний статистическим
методом. В частности, период автоколебаний в данном случае получается в
соответствии с выражением
T* = T+t1 + t2,
(18)
где t1, t2 – случайные задержки изменения коэффициента заполнения,
которые при несинхронизированных сигналах в цифровом регуляторе и
импульсном прерывателе можно принять равномерно распределенным в
интервале времени 01/, где – рабочая частота импульсного прерывателя.
Амплитуда гладкой составляющей, т.е. средних за период регулирования
значений тока, при этом также может увеличиваться, достигая значения
A*=A+ΔI1+ΔI2, где I1, I2 – случайные изменения тока, соответствующие
дискретности изменения коэффициента заполнения k =1/(2N–1), где N –
количество разрядов выходного регистра или счетчика.
17
При этом условии предельное значение указанных случайных
составляющих можно оценить как T1max T2max kYm.
Практические расчеты цифровых регуляторов тяговых электроприводов
показывают, что деформация фазового портрета, построенного для гладкой
составляющей, из-за импульсного характера работы исполнительного элемента
может составлять около 4-8 % от соответствующих значений, полученных для
идеального регулирования. Детальные исследования указанной деформации
фазового портрета выполнены методом статистического компьютерного
моделирования. В результате установлено, что случайные величины t1, t2, I1,
I2, действительно подчиняются равномерному распределению с указанными
выше граничными значениями. На основании этого при практических расчетах
целесообразно пользоваться приведенными упрощенными формулами для
расчета деформации (расплывания) фазового портрета.
Одно из принципиальных отличий цифровых регуляторов от классических
регуляторов аналогового типа связано с наличием задержки τ сигнала в
цифровом управляющем элементе. В простейших цифровых регуляторах эта
задержка объясняется тем, что задающий генератор импульсов переключает
счетчик номера позиции лишь в дискретные моменты времени, а не сразу при
появлении рассогласовании I > . Указанная задержка может быть
исключена, но это усложняет регулятор. В микропроцессорных системах
причиной задержки является программная обработка сигнала, а также процесс
преобразования входных сигналов в цифровую форму при приеме информации
с аналоговых или частотных датчиков. Как показали статистические
исследования, указанная задержка может рассматриваться как случайная
величина., описываемая распределением вероятностей р(), которое обычно
является равномерным, нормальным или логарифмическим нормальным.
Равномерное распределение (рис. 8, а) имеет место в простейших
цифровых регуляторах. Нормальное распределение (рис. 8, б) характерно для
более сложных систем, в том числе для систем с программной обработкой
информации при наличии условных переходов и циклов или же в случае
зависимости длительности выполняемых арифметических и логических
операций от значений от числа разрядов операндов. Логарифмическое
нормальное распределение (рис. 8, в) наблюдается при достаточно сложных
программах управления со значительным числом условных переходов и циклов,
а также в многопрограммных управляющих компьютерах.
Рассматриваемая задержка не оказывает влияния на условия
возникновения
автоколебаний
и
на
вероятностные
зависимости,
характеризующие возможное число состояний устойчивого равновесия
системы. Остаются справедливыми и выражения для расчета вероятности
нахождения системы в состоянии, определяемом количеством положений
18
равновесия Ny и Ny. Влияние задержки проявляется лишь в случае
возникновения автоколебаний и сказывается на изменении их амплитудновременных параметров.
Наличие случайной задержки > 0 приводит к тому, что автоколебания в
цифровой системе регулирования становятся непериодическими (рис. 8), а
точнее в большинстве практически важных случаев они могут быть отнесены к
классу почти периодических колебаний. Это позволяет рассматривать их как
комбинацию рассмотренной в разделе 3 регулярной составляющей с периодом Т
и амплитудой А = 2 и случайной составляющей, которая является функцией .
При этом чисто периодическая составляющая обычно является превалирующей
и составляет до 85-95 % амплитуды автоколебаний. Несмотря на то, что
рассматриваемый автоколебательный процесс становится апериодическим, для
его математического описания целесообразно воспользоваться терминологией
периодических процессов. В соответствии с этим будем рассматривать
амплитуду и период автоколебаний, интерпретируя их как случайные величины,
которые могут быть описаны распределениями вероятностей.
а)
б)
в)
p
p
p
τ
τ
0
τmax τ
0
τ τmax τ
0
b
B
τ
τ
г)
I(t)
I0
b
b
B
b
c
c
c
Iэ
t
d
I′0
d
a
a
D
D
Рис. 8. Характерные распределения случайной задержки τ (а, б, в) и зависящие
от нее непериодические автоколебания (г)
19
Указанные регулярную (чисто периодическую) и случайную составляющие
квазистационарного процесса с автоколебаниями удобно представить на
фазовой плоскости (рис. 9). При этом фазовый портрет 1234 идеализированного
цифрового регулятора расширяется за счет того, что линии переключения 23 и
14 смещаются от центра фазового портрета по горизонтали. Конкретная
реализация фазового портрета за период колебания представлена как 1'2'3'4', а
предельное положение фазового портрета обозначено 1"2"3"4". Фазовый
портрет может занимать любое положение в промежутке между 1234 и 1"2"3"4";
зона возможных положений фазового портрета заштрихована на рис. 9.
Временные и амплитудные параметры, характеризующие случайное
положение фазового портрета 1234, могут быть определены из указанного выше
положения о композиции детерминированного чисто периодического колебания
с периодом Т и амплитудой А и случайного колебания, которое появляется из-за
наличия задержки > 0. При этом период результирующего случайного
колебания 1'2'3'4' равен
T =T+2+3+4+1,
(19)
где 2, 4 – реализация случайной величины , которые соответствуют задержкам
переключения системы с траектории Ym+1 на Ym, т.е. по линии 2'3', и наоборот – с
траектории Ym на Ym+1, т.е. по линии 4'1';
3, 1 – функции реализации 2 и 4 соответственно, равные времени
движения изображающей точки в промежутках 3'3 и 1'1.
С учетом сделанного ранее допущения о линейности фазовых траекторий
вблизи оси абсцисс можно представить функции 3 и 1 следующим образом
I 0,m ( I з )
1
ln
,
ym 0 I 0,m ( I з A2 )
(20)
I 0,m1 ( I з )
1
ln
,
ym 0 I 0,m1 ( I з A4 )
(21)
3
1
где A2, A4 – изменения тока тягового двигателя в результате задержки
переключения системы в точках 2' и 4', определяемые, в свою очередь, через
задержки 2 и 4 как
A2 =(Im+1,0–Iз–)(1–e–2Ym+1,0),
(22)
A4 =(Iз+–Imo)(1–e–4Ym0).
(23)
Аналогичным образом, используя метод композиции, т.е. наложение чисто
периодического и случайного режимов, можно представить амплитуду
результирующего
почти
периодического
колебания
как
сумму
детерминированной и случайной составляющих
A=A+A2+A4,
(24)
20
где А = 2 – амплитуда автоколебаний, соответствующая идеальному фазовому
портрету 1234, т.е. при = 0.
В ряде практических задач достаточно знать лишь предельные положения
фазового портрета 1234 и 1"2"3"4". Параметры первого из них определяются
выражениями для идеального цифрового регулятора, а параметры второго –
выражениями для Т ' и А' при подстановке в них вместо его предельного
значения max. Его определяют как граничные оценки распределения р( ) при
доверительной вероятности 0.95 или 0.99.
1
Y
1′ 1
d(i iз )
dt
2
ΔA4
2′
2
′
ΔA4
δ
-δ
(i-Iз)
ΔI2′
0
ΔI 2
4
4′ 4
3
A
A′
A
3′ 3
Рис. 9. Фазовой портрет случайных автоколебаний
Указанным образом получаем формулы для оценки предельных значений
периода Т" и амплитуды А" почти периодических автоколебаний ТЭД
T = T+2max+3(max)+1(max),
(26)
A = 2+Im0(1–e–maxYm0).
(27)
Следовательно, почти периодические автоколебания 1(t) могут быть
охарактеризованы случайными величинами Т' и А'. Последние описываются
21
условными распределениями вероятностей рyy (Т') и рyy (А'). Если не
фиксировать параметр Y, то получим условные распределения р y (Т') и рy (А'),
которые являются композицией каждого из указанных выше распределений р yy
(Т ') и рyy (А') с равномерным распределением р(Y). Распределение р(Y)
соответствует возможному интервалу изменения Y от нуля до Ymax=Im0Ym0.
Конкретный вид исходных условных распределений рyy(Т') и рyy(А') зависит
от распределения р(). Однако, распределение рyy(Т') обычно бывает усеченным
нормальным или логарифмическим нормальным, а распределение р yy(А') –
усеченным нормальным. Параметры всех указанных распределений могут быть
определены методом композиции распределений или же методом
статистических испытаний путем компьютерного моделирования. Однако,
применение метода композиции распределений затруднительно из-за сложности
исходных выражений, а метод статистических испытаний при использовании
его в стандартном виде требует значительных затрат времени, поскольку
исследуемый процесс характеризуется тремя степенями свободы. Для
исключения указанного затруднения разработана методика комбинированного
типа, которая предполагает совместное использование методов композиции и
статистического моделирования. Однако, во многих практически важных
случаях вполне достаточно бывает предельных оценок временных и
амплитудных параметров почти периодических автоколебаний. Эта задача
решается на основе выражений для Т" и А" при подстановке в них
соответствующих параметров тягового электропривода, зависящих от режима
его работы, т.е. от заданного тока Iз и от частоты вращения n.
В пятой главе представлена оценка экономической эффективности
выполненной разработки. Итоговые данные по энергосбережению могут быть
оценены так: от безреостатного пуска 7,9 %, от рекуперации 11,2 %. Эти
результаты могут быть экстраполированы на проектируемый метрополитен г.
Янгона (Союз Мьянма).
ЗАКЛЮЧЕНИЕ
1. Анализ систем импульсного регулирования при проектировании
электрооборудования для перспективных электропоездов постоянного тока
следует выполнять комплексно с учетом взаимодействия силового импульсного
преобразователя, тяговых двигателей и системы автоматики. Рекомендована
структура электрических силовых цепей электропоезда с минимальным
временем использования импульсного преобразователя при пуске двигателей –
только в области до выхода на естественную характеристику. После этого
должен работать контур автоматического ограничения скорости.
22
2. Система автоматического регулирования движения электропоезда с
импульсными преобразователями должна выполняться как 2-контурная система
подчиненного регулирования со стабилизацией тока во внутренних
параллельных контурах, количество которых равно числу импульсных
преобразователей, и с ограничением скорости поезда на заданном уровне во
внешнем контуре.
3. Процессы
импульсного
регулирования
тяговых
двигателей,
характеризующиеся сравнительно небольшим диапазоном пульсаций тока (610%), могут быть рассчитаны на основе предложенных в работе моделей
тягового двигателя, импульсного преобразователя
и автоматического
регулятора с обратной связями. Указанная модель при ряде обоснованных в
диссертации
допущений
позволяет
выполнить
совместной
расчет
электромагнитных и механических процессов в системе. Комплексный расчет
систем регулирования режимов работы электропоездов должен проводиться с
учетом импульсного характера функционирования исполнительного элемента и
нелинейностей тягового двигателя и регулятора (в понятие нелинейности
входит дискретность). Соответствующая методика разработана на базе метода
фазовой плоскости, реализуемого в графической и численно-аналитической
форме.
4. Перспективные системы регулирования тяговых электроприводов
целесообразно выполнять на цифровом принципе и учитывать специфические
для цифровых систем эффекты – наличие нескольких состояний устойчивого
равновесия в системе регулирования (бифуркация) и возникновение
непериодических колебаний. Предложенная в работе методика статистического
моделирования процессов цифрового регулирования разделена на 5 этапов и
дополнена в целях экономии машинного времени ЭВМ методом композиции
вероятностных распределений, описывающих частотно-амплитудные параметры
непериодических колебаний тягового тока. В результате получены обобщенные
распределения усеченного нормального вида, которые характеризуют
функционирование цифрового регулятора во всем диапазоне возможных
нагрузок и скоростей тягового электропривода. Эти данные могут быть учтены
при оценке мещающего влияния электропоезда на железнодорожную
автоматику.
5. Комплексная методика поэтапного анализа процессов цифрового
регулирования тягового электропривода с учетом бифуркаций и
непериодических автоколебаний может быть рекомендована для использования
при обосновании технических условий и технических требований для
электрооборудования вагонов метрополитена г. Янгона (Мьянма).
23
Основные положения диссертации опубликованы в следующих работах:
1. Ко Ко Зо. Анализ электромагнитных процессов импульсного
регулирования тягового электродвигателя постоянного тока //
Труды 5-й научно-практической конференции «Безопасность
движения поездов». – М.: МИИТ, 2008. – с. 108-109.
2. Ко Ко Зо. Квазипериодические автоколебания в системе цифрового
регулирования электроприводов с двигателями постоянного тока.
Вестник МИИТа, 2008, вып. 19, – с. 51-56.
3. Ко Ко Зо. Обеспечение безопасной эксплуатации импульсных
преобразователей в электрической тяге постоянного тока // Труды
9-й научно-практической конференции «Безопасность движения
поездов». – М.: МИИТ, 2008. – с. V-2.
4. Ко Ко Зо. Обеспечение электробезопасности силового
оборудования для электропоездов// Труды 8-й научно-практической
конференции «Безопасность движения поездов», в 2.т, т.1. – М.:
МИИТ, 2007. – с. V-43.
5. Ко Ко Зо. Расчет процессов импульсного регулирования тягового
электродвигателя
постоянного
тока.
–
Электроника
и
электрооборудование транспорта, 2008, № 1, – с. 8-9.
Ко Ко Зо
ПРОЦЕССЫ РЕГУЛИРОВАНИЯ ТЯГОВОГО ЭЛЕКТРОДВИГАТЕЛЯ
ПРИ ПИТАНИИ ОТ ИМПУЛЬСНОГО ПРЕОБРАЗОВАТЕЛЯ
Специальность 05.09.03 –
Электротехнические комплексы и системы
Подписано к печати 26.04.10.
Объем 1,5 п.л.
Печать офсетная.
Формаг 60×80 1/16
Заказ № 287
Тираж 80 экз.
Бумага для множительного аппарата.
Типография МИИТ 127994, г. Москва, ул. Образцова, д. 9, стр. 9
24