Рабочая программа - Чувашский государственный университет

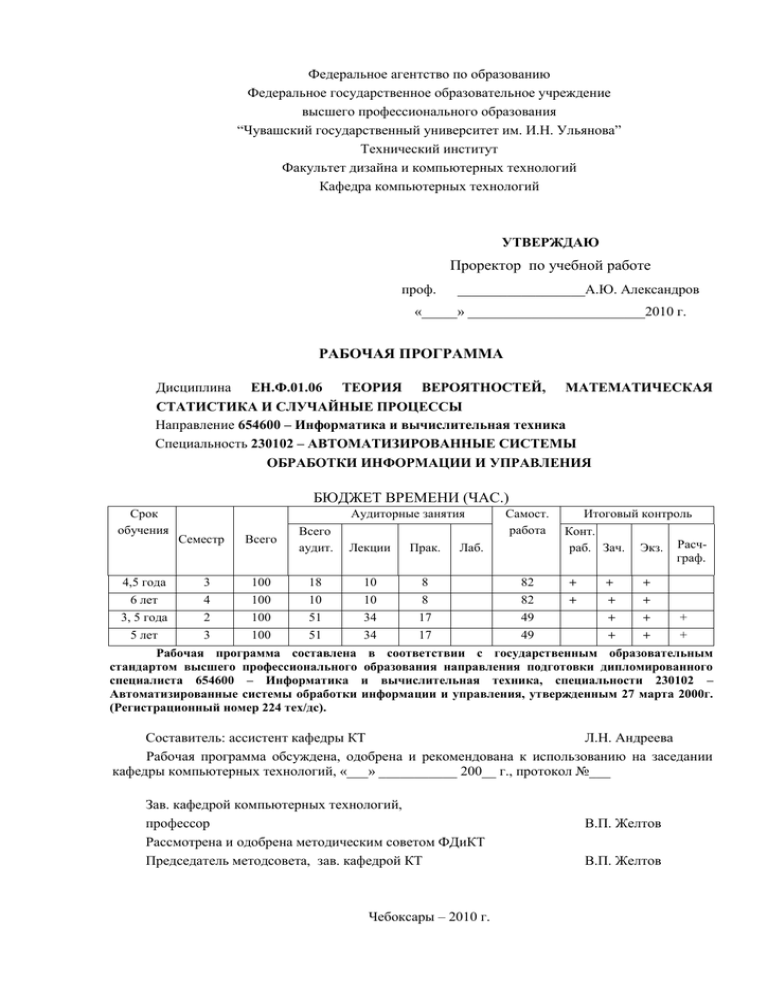
Федеральное агентство по образованию
Федеральное государственное образовательное учреждение
высшего профессионального образования
“Чувашский государственный университет им. И.Н. Ульянова”
Технический институт
Факультет дизайна и компьютерных технологий
Кафедра компьютерных технологий
УТВЕРЖДАЮ
Проректор по учебной работе
проф.
__________________А.Ю. Александров
«_____» _________________________2010 г.
РАБОЧАЯ ПРОГРАММА
Дисциплина ЕН.Ф.01.06 ТЕОРИЯ ВЕРОЯТНОСТЕЙ, МАТЕМАТИЧЕСКАЯ
СТАТИСТИКА И СЛУЧАЙНЫЕ ПРОЦЕССЫ
Направление 654600 – Информатика и вычислительная техника
Специальность 230102 – АВТОМАТИЗИРОВАННЫЕ СИСТЕМЫ
ОБРАБОТКИ ИНФОРМАЦИИ И УПРАВЛЕНИЯ
БЮДЖЕТ ВРЕМЕНИ (ЧАС.)
Срок
обучения
4,5 года
6 лет
3, 5 года
5 лет
Аудиторные занятия
Семестр
3
4
2
3
Всего
Всего
аудит.
Лекции
Прак.
100
100
100
100
18
10
51
51
10
10
34
34
8
8
17
17
Рабочая программа составлена
стандартом высшего профессионального
специалиста 654600 – Информатика
Автоматизированные системы обработки
(Регистрационный номер 224 тех/дс).
Самост.
работа
Лаб.
82
82
49
49
Итоговый контроль
Конт.
раб. Зач. Экз. Расчграф.
+
+
+
+
+
+
+
+
+
+
+
+
в соответствии с государственным образовательным
образования направления подготовки дипломированного
и вычислительная техника, специальности 230102 –
информации и управления, утвержденным 27 марта 2000г.
Составитель: ассистент кафедры КТ
Л.Н. Андреева
Рабочая программа обсуждена, одобрена и рекомендована к использованию на заседании
кафедры компьютерных технологий, «___» ___________ 200__ г., протокол №___
Зав. кафедрой компьютерных технологий,
профессор
Рассмотрена и одобрена методическим советом ФДиКТ
Председатель методсовета, зав. кафедрой КТ
Чебоксары – 2010 г.
В.П. Желтов
В.П. Желтов
1. ЦЕЛИ И ЗАДАЧИ ИЗУЧЕНИЯ ДИСЦИПЛИНЫ
Цель дисциплины - изучить основные понятия и закономерности теории
вероятностей, математической статистики и случайных процессов. Способствовать
формированию у студентов научного мировоззрения и системного мышления. Развить
логическое мышление студентов, привить потребность теоретического осмысления и
обоснования различных явлений.
Задачи дисциплины:
- изучение случайной величины, ее функции распределении, математическое ожидание
и дисперсии;
- изучение распределение монотонной функции от случайной величины;
- изучение системы случайных величин, условные плотности, зависимости и
независимости случайных величин, корреляционного момента;
- изучение закона больших чисел и центральной предельной теоремы;
- изучение критерии статических характеристик случайных процессов;
- изучение стационарных случайных процессов;
- изучение методов статистических испытаний;
2. УМЕНИЕ И НАВЫКИ
Студент должен:
 иметь представление о случайных событиях, случайных величинах, системах
случайных величин, способах их задания, об основных распределениях случайных
величин, о случайных процессах, о методах систематизации и обработки статистических
данных.
 знать и уметь использовать понятия и методы теории вероятностей и
математической статистики в своей профессиональной деятельности.
 владеть: основными приемами вычисления вероятностей случайных событий,
случайных величин и систем случайных величин.
 иметь опыт: практических расчетов вероятностей случайных событий, случайных
величин и систем случайных величин, числовых характеристик, статистических оценок
параметров распределения.
3. СОДЕРЖАНИЕ ДИСЦИПЛИНЫ
Тема 1. Предмет теории вероятностей. Примеры теоретико-вероятностных задач.
Виды случайных событий. Случайные события как подмножества множества простейших
исходов. Основные понятия алгебры событий.
Тема 2. Классическая вероятностная схема. Свойства вероятности. Статистическая и
геометрические вероятности. Основные формулы комбинаторики.
Теорема сложения вероятностей несовместных событий. Полная группа событий.
Противоположные события.
Тема 3. Теорема умножения вероятностей. Вероятность появления хотя бы одного
события. Теорема сложения вероятностей совместных событий. Система гипотез.
Формула полной вероятности. Формулы Байеса.
Тема 4. Определение, примеры, виды, способы задания случайных величин. Закон
распределения вероятностей дискретной случайной величины. Функция распределения
вероятностей и ее свойства. Плотность распределения вероятностей непрерывной
случайной величины и ее свойства.
Тема 5. Числовые характеристики случайных величин: математическое ожидание,
дисперсия, среднее квадратическое отклонение, - и их свойства. Начальные и центральные
моменты. Асимметрия. Эксцесс.
Тема 6. Основные распределения дискретных случайных величин: биномиальное
распределение,
распределение
Пуассона,
геометрическое
и
гипергеометрическое
распределения, - и их характеристики. Локальная и интегральная теоремы МуавраЛапласа.
Тема 7. Основные распределения непрерывных случайных величин: равномерное,
показательное, нормальное, - и их характеристики. Влияние параметров нормального
распределения на форму нормальной кривой. Вероятность попадания нормальной
случайной величины в заданный интервал. Вычисление вероятности заданного
отклонения. Правило трех сигм.
Тема 8. Понятие о системе нескольких случайных величин. Закон распределения
вероятностей дискретной двумерной случайной величины. Функция распределения
двумерной случайной величины и ее свойства.
Тема 9. Плотность распределения вероятностей двумерной непрерывной случайной
величины и её свойства. Функция и плотность распределения n-мерной случайной
величины. Условные законы распределения составляющих системы случайных величин.
Условные функция и плотность распределения.
Тема 10. Числовые характеристики системы двух случайных величин. Зависимые и
независимые случайные величины. Числовые характеристики зависимости (ковариация,
коэффициент корреляции).
Тема 11. Двумерное нормальное распределение. Вероятность попадания в эллипс
равной вероятности. Общий случай n-мерного нормального распределения. Функции от
нормально распределенных случайных величин. Распределения "хи-квадрат", Стьюдента,
Снедекора-Фишера. Полиномиальное распределение.
Тема 12. Одинаково распределенные взаимно независимые случайные величины.
Неравенство Чебышева. Теорема Чебышева. Закон больших чисел. Теорема Чебышева и
её частные случаи. Центральная предельная теорема.
Тема 13. Понятие о случайном процессе. Случайный процесс с дискретным и с
непрерывным временем, с дискретными и непрерывными значениями. Примеры.
Марковский случайный процесс. Вероятности состояний и переходные вероятности.
Понятие однородного марковского процесса.
Тема 14. Цепи Маркова. Матрица вероятностей переходов. Однородная цепь
Маркова. Предельные вероятности состояний.
Тема 15. Марковский процесс с дискретными состояниями и непрерывным
временем. Уравнения Колмогорова.
Тема 16. Поток событий. Простейший поток и его свойства. Нестационарный
пуассоновский поток. Время обслуживания.
Тема
17.
Задачи
математической
статистики.
Генеральная
и
выборочная
совокупности. Выборки. Способы отбора. Статистическое распределение выборки.
Эмпирическая функция распределения. Полигон и гистограмма.
Тема 18. Статистические оценки параметров распределения. Несмещенные,
эффективные и состоятельные оценки. Генеральная и выборочная средние. Групповая и
выборочная средние. Отклонение от общей средней и его свойство.
Тема 19. Генеральная и выборочная дисперсии. Формула для вычисления дисперсии.
Групповая, внутригрупповая, межгрупповая и общая дисперсии. Сложение дисперсий.
4. ПРАКТИЧЕСКИЕ ЗАНЯТИЯ
1. Классическая вероятностная схема. Теоремы сложения и умножения вероятностей.
2. Формула полной вероятности. Формулы Байеса.
3 Способы задания и числовые характеристики случайных величин.
4. Основные распределения случайных величин.
5. Система двух случайных величин. Функция и плотность распределения. Числовые
характеристики зависимости.
6. Двумерное нормальное распределение. Предельные теоремы.
7. Цепи Маркова.
8. Марковский процесс с дискретными состояниями и непрерывным временем.
9. Статистические оценки параметров распределения.
5. ЗАЧЕТНЫЕ И ЭКЗАМЕНАЦИОННЫЕ ВОПРОСЫ
1. Случайные события.
2. Алгебра событий.
3. Классическое определение вероятности.
4. Геометрическая вероятность.
5 Сложение и умножение вероятностей.
6 Форма полной вероятности.
7 Формула Байеса
7 Формула Бернулли.
9 Формулы локальной и интегральной теоремы Лапласа.
10. Дискретные, случайные непрерывные величины.
11. Закон, функции распределения.
12. Числовые характеристики.
13- Биноминальные распределения.
14.Распределение. Пуассона.
15. Показательное распределение.
16. Номинальные распределения.
17. Закон больших чисел.
18. Закон больших чисел и центральная предельная теорема
19.Точечные и интегральные оценки случайных величин.
20. Системы случайных величин.
21.Условные плотности.
22. Зависимость и независимость случайных величин. Корреляционный момент
23.Элементы математической статистики.
24.Выборочный метод.
25 Точечные оценки неизвестных параметров распределения по выборке.
26. Понятие о доверительных интервалах
27. Понятие о статической проверке гипотез и критериях согласия к их применению к
обработке результатов эксперимента.
28. Критерии проверки гипотез.
29 Статистические характеристики случайных процессов.
30. Стационарный случайный процесс.
31. Метод статистических испытаний.
ЛИТЕРАТУРА
1. Вентцель Е.С.Теория вероятностей: Учебник для вузов. – 7-е изд. – М.: Высш. шк.,
2001. – 575 с.
2. Гмурман В. Е. Теория вероятностей и математическая статистика: Учеб. пособие.
(ГРИФ) – М.: Высш. шк., 2004. – 479 с.
3. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической
статистики: Учебное пособие.- М.: Высш. Шк., 2001. – 400 c.
4. Гнеденко Б.В. Курс теории вероятностей: Учебник. – изд-е 6-е, перераб, и доп. – М.:
Наука, 1988.- 448 с.
5. Горелова Г.В. Теория вероятностей и математическая статистика в примерах и задачах
с применением Excel: Учеб. пособие для вузов / Г.В. Горелова, И А. Кацко. - 2-е изд.
испр., и доп. - Ростов н/Д: Феникс, 2002. – 398 с.
6. Ефимов А.Е. Сборник задач по математике для вузов. Учебное пособие для втузов. – 3е изд. перераб. и доп. – М.: Издательство Физико-математической литературы, 2004. –
432 с.
7. Колемаев А.В., Теория вероятностей и математическая статистика. – М.: Высшая
школа, 1991. – 400 с.
8. Кремер Н.Ш. Теория вероятностей и математическая статистика. Учебник. (ГРИФ).
М.: ЮНИТИ-ДАНА, 2004. -573 с.