Тема II «Преобразование алгебраических выражений» 1. Многочлены 2.

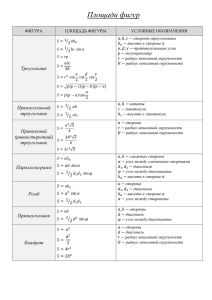
Тема II «Преобразование алгебраических выражений»
1. Многочлены.
Для любых a, b и c верны равенства:
2. Арифметическая прогрессия
(a1 – первый член; d – разность; n – число членов; an – n-й член; Sn – сумма n
первых членов):
3. Геометрическая прогрессия
(b1 – первый член; q – знаменатель; n – число членов; bn – n-й член; Sn –
сумма n первых членов, S – сумма бесконечной геом. прогрессии):
Соотношения между тригонометрическими функциями одного и того же аргумента
(здесь и в дальнейшем запись n є Z означает, что n – любое целое число)
Формулы преобразования произведения в сумму:
Формулы сложения:
Формула приведения для преобразования выражений вида
а) перед приведенной функцией ставиться тот знак, который имеет исходная функция;
б) функция меняется на «кофункцию», если n нечетно; функция не меняется, если n четно.
(Кофункциями синуса, косинуса, тангенса и котангенса называются соответственно
косинус, синус, котангенс и тангенс.) Например:
Формулы двойного аргумента:
Формулы тройного аргумента:
Формулы половинного аргумента:
(для функций sin и cos – формулы понижения степени)
Формулы кубов:
Формулы нахождения угла:
Формулы преобразования суммы в произведение:
ТАБЛИЦА ЗНАЧЕНИЙ
Произвольный треугольник:
Центр описанной окружности – точка пересечения серединных перпендикуляров. Центр
вписанной окружности – точка пересечения биссектрис. (a,b,c – стороны:
противолежащие им углы; p – полупериметр; R – радиус описанной окружности; r –
радиус вписанной окружности; S – площадь; ha – высота, проведенная к стороне a):
2. Прямоугольный треугольник: Центр описанной окружности совпадает с центром
гипотенузы. (a,b – катеты; c – гипотенуза; ac, bc – проекции катетов на гипотенузу):
3. Равносторонний треугольник: Медиана = биссектрисе. OR = Or.
2. Прямоугольный треугольник:
Центр описанной окружности совпадает с центром гипотенузы. (a,b – катеты; c –
гипотенуза; ac, bc – проекции катетов на гипотенузу):
3. Равносторонний треугольник:
Медиана = биссектрисе. OR = Or.
4. Произвольный выпуклый четырехугольник
(d1 и d2 – диагонали;
– угол между ними; S - площадь):
5. Параллелограмм
(a и b – смежные стороны;
– угол между ними; ha – высота, проведенная к стороне a):
6. Ромб:
В любой ромб можно вписать окружность.
7. Прямоугольник:
Около любого прямоугольника можно описать окружность.
8. Квадрат
(d – диагональ):
9. Трапеция
(a и b – основания; h – расстояние между ними; l – средняя линия):
10. Описанный многоугольник
(p – полупериметр; r – радиус вписанной окружности):
S = pr.
11. Правильный многоугольник
(an – сторона правильного n-угольника; R – радиус описанной окружности; r – радиус
вписанной окружности):
12. Окружность, круг
(r - радиус; C – длина окружности; S – площадь круга):
13. Сектор
(l – длина дуги, ограничивающей сектор;
радианная мера центрального угла):
- градусная мера центрального угла;
-