Построение графика квадратичной функции

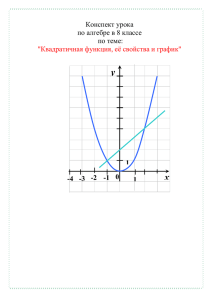
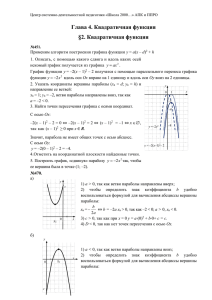
Построение графика квадратичной функции
Цели: повторить понятие квадратичной функции;
повторить алгоритм построения параболы сдвигами;
закрепить умение определять свойства квадратичной функции по графику.
Образовательные:
совершенствовать знания по следующим направлениям:
-нахождение вершины квадратичной функции;
-построение графика квадратичной функции;
-графическое решение квадратных уравнений.
Воспитательные:
воспитывать аккуратность при построении чертежей и работе на доске,
умение работать в группе.
Развивающие:
развивать вычислительные навыки и пространственное мышление учащихся, мыслительные
операции.
Ход урока.
1Организационный момент.
Учитель знакомит с целями урока, рассказывает план урока. Учащиеся в
тетрадях записывают тему урока, подписывают листочки с тестами.
2АКТУАЛИЗАЦИЯ. Устная работа. (Обобщение, пространственное мышление).
-Какая функция называется квадратичной? (Функция вида у=ах2+bх+с
называется квадратичной).
-По каким точкам строиться график функции у = x2 ?
-Выясните вверх или вниз направлены ветви параболы? (Анализ)
у=4х2-5х+1
у=-3х2+6х-4
у=12х -5 х2-1
у= 7+8х+9х2
-Не выполняя построения графика функции у=-3х2 -6х+1, ответьте на вопросы:
(синтез)
-Какая прямая служит осью параболы? (х0=-1)
-Каковы координаты вершины параболы? (-1;4)
-Чему равно наименьшее и наибольшее значение функции? (унаибольшее=4;
унаименьшее не существует).
-Как построить графики следующих функций:у = (х – 3)^2 + 3 у = (х + 3)^2 – 9
у = (5 + x)^2 + 4 у = х^2 + 2 у = (х – 7)^2.
3 Изучение темы.
ИЗУЧЕНИЕ АЛГОРИТМА ПОСТРОЕНИЯ ГРАФИКА КВАДРАТИЧНОЙ ФУНКЦИИ
ЗАДАЧА 1.построить график функции y = x2+x-2 и записать свойства данной
функции.
Алгоритм построения:
1Ветви параболы идут вверх.
2.x0 = -b/2a=-0,5, y0 = (-0,5)2-0,5-2 = -2,25, вершина (-0,5; -2,25). За единицу удобно
взять 2 клетки. Отмечаем ось симметрии параболы.
3.Точки пересечения с осью Оx: y=0, x2+x-2=0, x1=-2, x2=1, точки (-2;0) и (1;0). С
осью Оy: x=0, y=-2, точка (0;-2). Отмечаем точку, симметричную точке (0;-2),
относительно оси параболы: (-1;2)
4.Дополнительные точки: x=2, y=22+2-2=4, точка (2;4). Отмечаем точку,
симметричную точке (2;4), относительно оси параболы: (-3;4). Соединяем точки
плавной кривой.
Проблемные вопросы:
Какие значения принимает х (область определения функции)?
Какие значения принимает функция (множество значений функции)?
Назовите промежутки, на которых функция принимает положительные
(отрицательные) значения?
4.
Укажите промежутки возрастания (убывания) функции.
5.
Укажите наибольшее (наименьшее) значения функции.
1.
2.
3.
Свойства:
1.x – любое действительное число
2.y ³-2,25,
3..y>0 при x<-2, x>1; y=0 при x=-2 и x=1; y<0 при –2<x<1
4.возрастает при x ³-0,5, убывает при x £-0,5
5.ymin=-2,25 при x=-0,5.
Здания по вариантам:
№ п/п
1
2
3
4
5
6
Функция
y = x2-2x-8
y = -x2+4x+5
y= -x2+2x+8
y=x2-4x+7
y=-x2-6x-8
y=-x2-2x+3
Вершина
(1;-9)
(2;9)
(1; 9)
(2;3)
(-3; 1)
(-1;4)
Нули функции
x1=4, x2=-2
x1=5; x2=-1
x1=4 x2=-2
нет
x1=-2; x2=-4
x1=-3; x2=1
ИТОГ
Ход урока.
Тест 1.
Установите соответствие между квадратичной функцией и координатами
вершины.
Вариант 1.
Вариант 2.
2
у=3х -12х+10
(-4;-6)
у=х2+6х+8
(-1;6)
2
2
у=-х +4х+5
(2;-2)
у=-2х +8х-5
(2;3)
2
2
у=х +8х+10
(2;9)
у=-4х -8х+2
(-3;-1)
Весь класс выполняет этот тест на заготовленных карточках, двое
работают на створках доски. Затем проводят стрелки на интерактивной
доске, класс проверяет это задание. (Сравнение).
Задание 1. Постройте график функции: у= -х2+2х+3. Найдите наибольшее
и наименьшее значение функции на отрезке [0;2], на полуинтервале (1;3].
(Анализ)
у
1
Решение.
х0= -
b
2
1
=
2а  2
у0=-1+2+3=4
(1;4) – вершина параболы.
[0;2] : унаибольшее=4 (при х=1);
унаименьшее =3 (при х=0 и х=2).
(1;3] : унаибольшее=не существует
унаименьшее =0 (при х=3).
Задание 2. Найдите значение коэффициента с и постройте график
функции у=х2-6х+с, если известно, что наименьшее значение функции равно
1.
(Перенос знаний в новую ситуацию)
Решение.
х0= -
b
6
= 3
2а 2
9-18+с=1;
с=10.
Итак, задана функция
у=х2-6х+10.
у0=9-18+10=1.
(3;1) – вершина параболы.
Ответ: с=10.
Самостоятельная работа. (Аналогия, сравнение)
Вариант 1
Вариант2.
№ 1. Постройте график функции
№ 1. Постройте график
2
функции у=3х +6х+1.
у=2х2+4х+1. Найдите наибольшее и
Найдите
наибольшее
и
наименьшее значение
наименьшее значение функции на
функции на отрезке [-1;-2].
отрезке [-3;0].
Ответ: унаибольшее=7 (при х=-3);
Ответ: унаибольшее=1 (при х=-2);
унаименьшее =-1 (при х=-1).
унаименьшее =--2 (при х=1).
Вариант 1.
На рисунках представлены графики квадратичных функций. Заполнить таблицу.
1
2
у
у
-1
1
0
Вершина
возрастает
убывает
х
-1 0 1
-1
3
4
у
2
у
х
0
-2
5
-1
1
х
0
у
х
-1
1
1
0
х
Нули
функции
ось
симметрии
Наибольшее
и
наименьшее
значение.
№ п/п
1
2
Функция
y = x2-2x-8
y = -x2+4x+5
Вершина
Нули функции
Вариант2.
На рисунках представлены графики квадратичных функций. Заполнить таблицу.
1
2
у
-1 0 1
-1
Вершина
возрастает
убывает
Нули
функции
ось
симметрии
Наибольшее
и
наименьшее
значение.
№ п/п
1
2
3
у
2
х
-1
0
4
у
у
х
0
5
-1
1
1
0
х
у
х
-1
1
1
0
-2
Функция
y= -x2+2x+8
y=x2-4x+7
Вершина
Нули функции
Формулирует возможные настроения учащихся.
Если вам понравился урок и вы чувствуете, что тему поняли, то выбираете смайлик счастья.
Если урок понравился, но не всё ещё понятно, то смайлик печали.
Если и урок не понравился, и всё не понятно, то плачущий смайлик
х