Линденбаум М.Д., Маннанов Р.В. МЕТОДЫ СТАТИСТИЧЕСКОГО
реклама
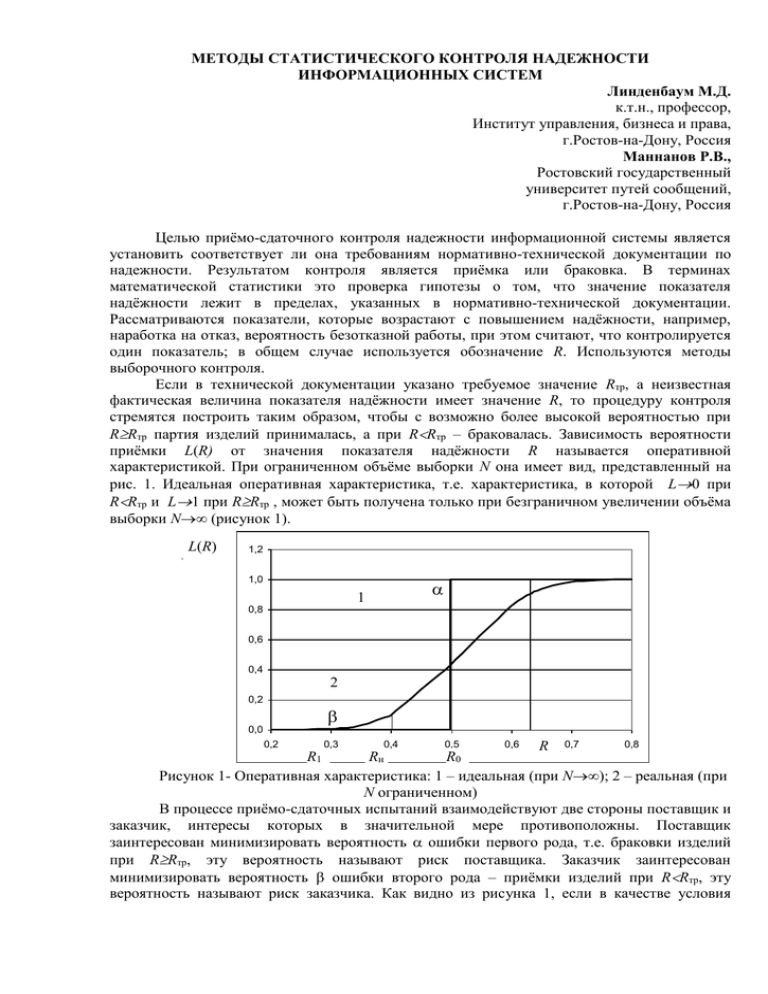
МЕТОДЫ СТАТИСТИЧЕСКОГО КОНТРОЛЯ НАДЕЖНОСТИ ИНФОРМАЦИОННЫХ СИСТЕМ Линденбаум М.Д. к.т.н., профессор, Институт управления, бизнеса и права, г.Ростов-на-Дону, Россия Маннанов Р.В., Ростовский государственный университет путей сообщений, г.Ростов-на-Дону, Россия Целью приёмо-сдаточного контроля надежности информационной системы является установить соответствует ли она требованиям нормативно-технической документации по надежности. Результатом контроля является приёмка или браковка. В терминах математической статистики это проверка гипотезы о том, что значение показателя надёжности лежит в пределах, указанных в нормативно-технической документации. Рассматриваются показатели, которые возрастают с повышением надёжности, например, наработка на отказ, вероятность безотказной работы, при этом считают, что контролируется один показатель; в общем случае используется обозначение R. Используются методы выборочного контроля. Если в технической документации указано требуемое значение Rтр, а неизвестная фактическая величина показателя надёжности имеет значение R, то процедуру контроля стремятся построить таким образом, чтобы с возможно более высокой вероятностью при RRтр партия изделий принималась, а при RRтр – браковалась. Зависимость вероятности приёмки L(R) от значения показателя надёжности R называется оперативной характеристикой. При ограниченном объёме выборки N она имеет вид, представленный на рис. 1. Идеальная оперативная характеристика, т.е. характеристика, в которой L0 при RRтр и L1 при RRтр , может быть получена только при безграничном увеличении объёма выборки N (рисунок 1). L(R) 1,2 ) 1,0 1 0,8 0,6 0,4 2 0,2 0,0 0,2 0,3 0,4 0,5 0,6 0,8 R 0,7 R1 Rн R0 Рисунок 1- Оперативная характеристика: 1 – идеальная (при N); 2 – реальная (при N ограниченном) В процессе приёмо-сдаточных испытаний взаимодействуют две стороны поставщик и заказчик, интересы которых в значительной мере противоположны. Поставщик заинтересован минимизировать вероятность ошибки первого рода, т.е. браковки изделий при RRтр, эту вероятность называют риск поставщика. Заказчик заинтересован минимизировать вероятность ошибки второго рода – приёмки изделий при RRтр, эту вероятность называют риск заказчика. Как видно из рисунка 1, если в качестве условия браковки и условия приёмки принять одно и то же значение Rтр, то, так как в любой точке оперативной характеристики +=1, одновременно оба риска минимизировать невозможно. Чтобы минимизировать оба риска возникает, необходимость установить два дополнительных уровня надёжности: приёмочный R1 и браковочный R0, которые устраивали бы и заказчика, и поставщика (R1RтрR0). Стороны договариваются о том, что заказчик принимает изделие по приёмочному уровню, а риск – это вероятность принять изделие при R=R1 или с ещё более низкой надёжностью; поставщик стремится представить на испытания изделия с показателем надёжности не ниже браковочного уровня, а риск – это вероятность того, что и при R=R0 или с ещё более высокой надёжности изделие всё же будет забраковано. Величины R1, R0, и являются предметом договоренности и устанавливаются в зависимости от затрат поставщика на повышение надёжности выше нормативной величины Rтр и от последствий недостаточной надёжности в эксплуатации у заказчика. Если эти затраты у поставщика и последствия у заказчика сопоставимы, то из условий паритета интересов принимают = и RТР R0 R1 . Организация приёмо-сдаточных испытаний включает три этапа: планирование, проведение и анализ полученных результатов. Две точки R1, и R0, 1- полностью задают оперативную характеристику и позволяют спланировать испытания. В результате планирования определяется объём испытаний V, а также правила браковки и приёмки. Следует иметь в виду, что при назначении уровней надёжности (R1, R0) и рисков (, ), необходимо учитывать реальные материальные и технические возможности: имеющееся число испытываемых изделий N, допустимое время испытаний T и другие. Приемо-сдаточные испытания бывают трех видов: 1. Однократная выборка. 2. Двукратная выборка. 3. Последовательный контроль. Наиболее часто используется метод однократной выборки. Метод однократной выборки сводится к организации испытаний в объёме V с фиксацией некоторого набора результатов x1, x2,…, xn. По окончании наблюдений вычисляется некоторая функция результатов наблюдений Х*(x1, x2,…, xn), область определения которой разделена на две непересекающиеся области Х1 и Х2. На основе полученных результатов принимается решение: если Х* попадает в область Х1, изделие принимается, если в область Х2 – бракуется. Наиболее просто задача решается при экспоненциальном законе распределения наработки на отказ. Для сложных информационных систем можно считать поток отказов простейшим, т.е. время между отказами подчиняется экспоненциальному закону распределения. В этом случае для выбора плана испытаний несущественны абсолютные значения уровней T0=R0 и T1=R1, а важно лишь их отношение = T0/T1 и риски и . При = и TТР T0 T1 , откуда T0 TTP , T1 TTP / , план испытаний полностью задаётся двумя величинами – и =. Для некоторого упрощения контрольной процедуры приёмкубраковку принято проводить не по уровню контролируемого показателя – наработке на отказ, а по числу возникших отказов, которые однозначно связаны. Для оценки параметров экспоненциального закона распределения достаточной статистикой являются суммарная наработка всех изделий t и число отказов r. План включает пару величин: предельную суммарную наработку tmax и браковочное число отказов rбр. Контроль прекращается, как только будет достигнуто одно из этих значений. Если первым достигается r=rбр при ttmax, то изделие бракуется, если первым достигается t=tmax при rrбр, то изделие принимается. На рисунке 2 представлена процедура испытаний при однократной выборке. Поскольку число отказов величина дискретная, при заданных значениях , и отношении =T0/T1 соответствующее точное решение тоже дискретно (1) T0 / T1 12 ,2 rбр / 2 ,2 rбр , t max / T0 1 / 2 2 ,2 rбр . (2) Существуют таблицы значений rбр и tmax/ T0 для планов приёмо-сдаточных испытаний методов однократной выборки при заданных значений = T0/T1 и рисков = 0,05 и 0,1 [1]. Метод однократной выборки позволяет спланировать испытания и при успешном их протекании по результатам уточнить риск заказчика. Недостаток этого метода состоит в том, что объем и время испытаний не зависит от фактической надежности системы. Только в случае браковки испытания могут завершиться существенно раньше по достижению rбр, но этот случай не представляет практический интерес. r Область браковки rбр Область приёмки 0 tmax t Рисунок 2- Процедура испытаний при однократной выборке Метод последовательных испытаний, разработанный Вальдом, позволяет сократить объем и время испытаний. В процессе испытаний фиксируются наработки и отказы изделий. Планирование состоит в том, что по заданным рискам и рассчитываются границы двух областей: браковки и приёмки. При этом в случае успешного или наоборот неблагоприятного протекания испытаний можно завершить их существенно раньше, сэкономить время и затраты на испытания. Правда, при последовательном контроле объём и время испытаний становятся случайными и зависят от соотношения гипотетического, положенного в основу планирования испытаний, и неизвестного фактического значений показателя надёжности. Если эти величины окажутся близкими, время испытаний может возрастать практически неограниченно. В связи с этим используют усечённый последовательный контроль, что приводит к некоторому возрастанию рисков и по сравнению с точным методом Вальда. Однако на практике этим широко пользуются, так как усечённый последовательный контроль позволяет в среднем уменьшить объём и время испытаний. При экспоненциальном законе распределения в процессе испытаний фиксируются только суммарная наработка по всем образцам t и суммарное число отказов r. Отказавшие элементы системы восстанавливаются. Планирование состоит в построении границ браковки и приёмки в координатах t/Т0 и rбр. Положение границ не зависит от абсолютных значений Т0 и Т1, а полностью определяется их отношением = T0/T1. В ходе испытаний строится ступенчатый график зависимости числа отказов от суммарной наработки, и в момент каждого очередного отказа принимается одно из трёх решений: - приёмка, если функция rбр(t) находится в области приёмки; - браковка, если функция rбр(t) находится в области браковки; - продолжение испытаний, если функция rбр(t) находится в промежуточной области. Границы областей приёмки и браковки представляют собой параллельные полубесконечные прямые линии: граница области приёмки r=r0+bt/T0, (3) граница области браковки r=b(t/T0 – t0/T0), (4) T0 / T1 1 ln[( 1 ) / ] t ln[ /( 1 )] где b , r0 , . ln( T0 / T1 ) T0 T0 / T1 1 ln( T0 / T1 ) Если =, то r=bt/T0 r0, где r0=bt/T0. Следует заметить, что наклон прямых b во всех случаях не зависит от рисков и определяется только отношением Т0/Т1. Для усечения процедуры контроля ограничивают число отказов и суммарную наработку значениями rус и tус, причём по достижении rус при t tус изделие бракуется, а по достижении tус при r rус изделие принимается. Значения параметров усечения rус и tус рассчитывают по rбр и tmax для однократной выборки. Увеличение rус и tус снижает риски, но может приводить к затягиванию испытаний, уменьшение – в среднем несколько сокращает время испытаний, но увеличивает риски заказчика и поставщика. Необходимо иметь в виду, что в данном методе решение должно приниматься только в момент очередного отказа, т.е. нельзя принимать решение сразу, как только произойдёт пересечение границы приёмки. Требуется продолжать испытание, по крайней мере, до очередного отказа, так как при этом траектория результатов может вернуться в зону продолжения контроля, и далее процесс может пойти как угодно. Вместе с тем, очередной отказ может произойти через большой промежуток времени, что существенно увеличит время испытаний. Процедура испытаний при последовательном контроле представлена на рисунке 3. r rус Область браковки Продолжение испытаний r0 Область приёмки 0 t/T0 tус t Рисунок 3 - Процедура испытаний при последовательном контроле Как уже выше говорилось, последовательный контроль позволяет завершить испытания раньше, чем в случае однократной выборки. Представляет большой практический интерес как уменьшение объема испытаний при увеличении фактической надежности системы. Эта задача не имеет аналитического решения, поэтому мы использовали метод статистических испытаний. Время между отказами, распределенное по экспоненциальному закону моделируется методом обратной функции по формуле t=–ln(1–r)T , (5) где r – случайная величина, распределенная по равномерному закону распределения в интервале [0;1]; T – наработка на отказ. Простейший поток отказов моделируется как последовательность экспоненциально распределенных случайных величин. Было проведено 1500 испытаний в пределах изменения фактической наработки на отказ Тф относительно к нормативной наработке Ттр в пределах от 1 до 1,875 с шагом 0,0625. уменьшение объема испытаний тоже измерялось в относительных единицах по отношению к объему испытаний для однократной выборки. На рисунке 4. приведена зависимость =tср/ tодн от относительной наработки = Тф/Ттр. tср/ tодн 1,2 1 0,8 0,6 0,4 0,2 0 1 1,2 1,4 Т /Т 1,6ф тр 1,8 2 Рисунок 4- Зависимость уменьшения объема испытаний от увеличения наработки на отказ; tср – средняя суммарная наработка при последовательном контроле; tодн –суммарная наработка при однократной выборке Полученная в результате моделирования зависимость =f() имеет сравнительно большой случайный разброс, поэтому было произведено сглаживание зависимости в рассматриваемых пределах методом наименьших квадратов. Полученная линейная зависимость =1,145–0,208 также представлена на рисунке 4. Как видно из рисунка, в пределах реального изменения надежности последовательный контроль позволяет уменьшить объем испытаний на 20 – 25% ЛИТЕРАТУРА 1. Линденбаум М.Д., Ульяницкий Е.М. Надежность информационных систем: Учебник для вузов ж.-д. транспорта. – М.: ГОУ «Учебно-методический центр по образованию на железнодорожном транспорте», 2007. – 318 с.