Формулы для длины окружности и её дуг
реклама
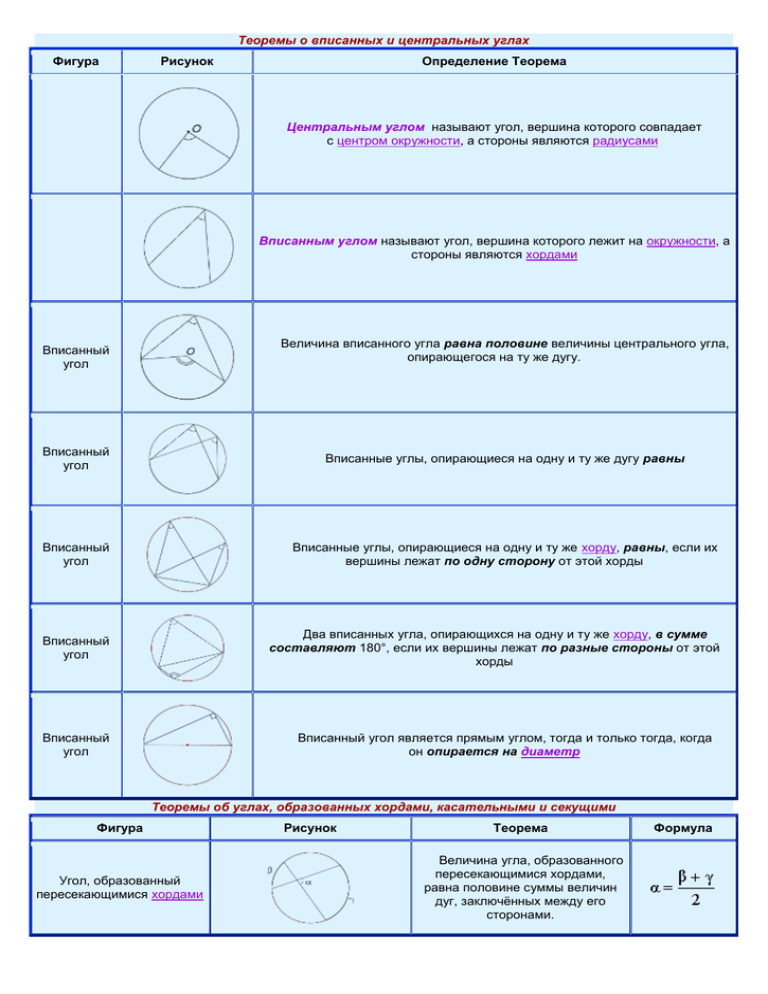
Теоремы о вписанных и центральных углах Фигура Рисунок Определение Теорема Центральным углом называют угол, вершина которого совпадает с центром окружности, а стороны являются радиусами Вписанным углом называют угол, вершина которого лежит на окружности, а стороны являются хордами Величина вписанного угла равна половине величины центрального угла, опирающегося на ту же дугу. Вписанный угол Вписанный угол Вписанные углы, опирающиеся на одну и ту же дугу равны Вписанный угол Вписанные углы, опирающиеся на одну и ту же хорду, равны, если их вершины лежат по одну сторону от этой хорды Вписанный угол Два вписанных угла, опирающихся на одну и ту же хорду, в сумме составляют 180°, если их вершины лежат по разные стороны от этой хорды Вписанный угол Вписанный угол является прямым углом, тогда и только тогда, когда он опирается на диаметр Теоремы об углах, образованных хордами, касательными и секущими Фигура Угол, образованный пересекающимися хордами Рисунок Теорема Величина угла, образованного пересекающимися хордами, равна половине суммы величин дуг, заключённых между его сторонами. Формула Угол, образованный секущими, которые пересекаются вне круга Величина угла, образованного секущими, пересекающимися вне круга, равна половине разности величин дуг, заключённых между его сторонами Угол, образованныйкасательной ихордой, проходящей через точку касания Величина угла, образованного касательной и хордой, проходящей через точку касания, равна половине величины дуги, заключённой между его сторонами Угол, образованный касательной и секущей Величина угла, образованного касательной и секущей, равна половине разности величин дуг, заключённых между его сторонами Угол, образованный двумя касательными к окружности Величина угла, образованного двумя касательными к окружности, равна половине разности величин дуг, заключённых между его сторонами Свойства хорд и дуг окружности Фигура Рисунок Свойство Диаметр, перпендикулярный к хорде Диаметр, перпендикулярный к хорде, делит эту хорду и стягиваемые ею две дуги пополам. Диаметр, проходящий через середину хорды Диаметр, проходящий через середину хорды, перпендикулярен к этой хорде и делит стягиваемые ею две дуги пополам. Равные хорды Если хорды равны, то они находятся на одном и том же расстоянии от центра окружности. Хорды, равноудалённые от центра окружности Если хорды равноудалены (находятся на одном и том же расстоянии) от центра окружности, то они равны. Две хорды разной длины Большая из двух хорд расположена ближе к центру окружности. Равные дуги У равных дуг равны и хорды. Теоремы о длинах хорд, касательных и секущих Фигура Пересекающиеся хорды Рисунок Теорема Произведения длин отрезков, на которые разбита каждая из хорд, равны: Если к окружности из одной точки проведены две касательных, то длины отрезков касательных от этой точки до точек касания с окружностью равны. AB = AC Касательные, проведённые к окружности из одной точки Касательная и секущая, проведённые к окружности из одной точки Справедливо равенство Секущие, проведённые из одной точки вне круга Справедливо равенство: Формулы для площади круга и его частей Числовая характеристика Рисунок Площадь круга Формула , где R – радиус круга, D – диаметр круга , если величина угла α выражена в радианах Площадь сектора , если величина угла α выражена в градусах , если величина угла α выражена в радианах Площадь сегмента , если величина угла α выражена в градусах Формулы для длины окружности и её дуг Числовая характеристика Длина окружности Рисунок Формула C = 2πR = π D, где R – радиус круга, D – диаметр круга L(α) = αR, если величина угла α выражена в радианах Длина дуги , если величина угла α выражена в градусах Свойства описанного и вписанного четырёхугольников. Числовая характеристика Рисунок Свойство Если четырёхугольник описан около окружности, то суммы длин его противоположных сторон равны. Если четырёхугольник вписан в окружность, то суммы величин его противоположных углов равны 180°. Теорема Птолемея. Произведение диагоналей вписанного четырёхугольника равно сумме произведений противоположных сторон. . Если координаты вектора заданы, его длина находится по формуле Скалярным произведением векторов называется произведение длин векторов на косинус угла между ними. . А вот так скалярное произведение выражается через координаты векторов Из формулы для скалярного произведения можно найти угол между векторами: и :