Система уравнений Максвелла

№
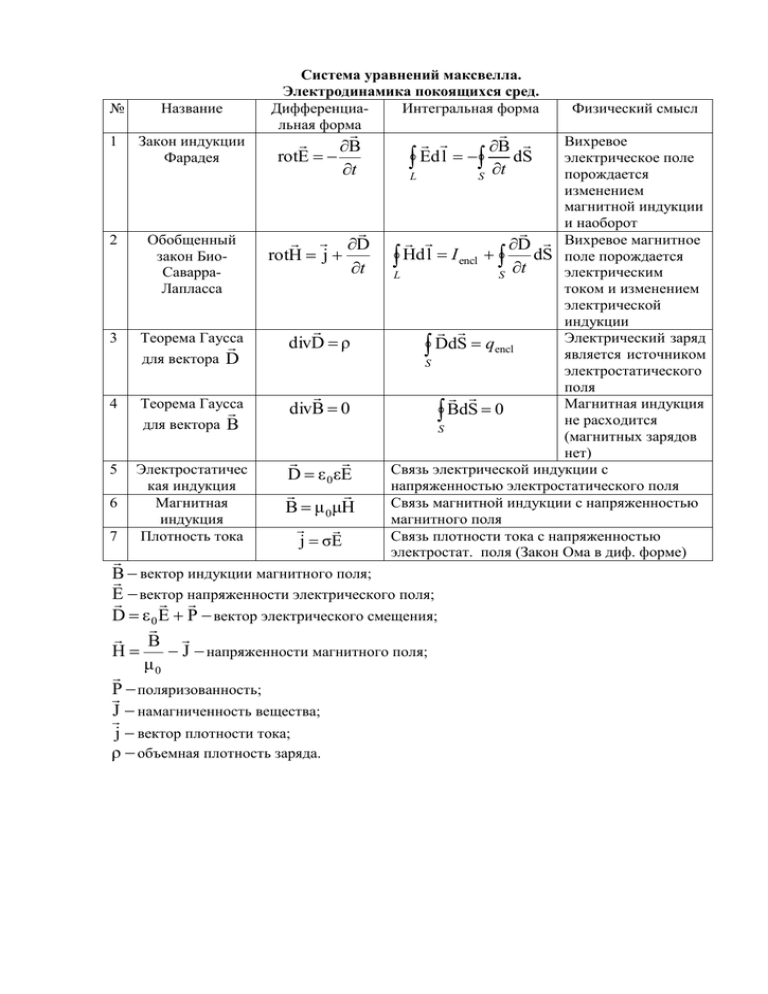
Название
1
Закон индукции
Фарадея
2
Обобщенный
закон БиоСаварраЛапласса
3
Теорема Гаусса

для вектора D
4
Теорема Гаусса

для вектора B
5
Электростатичес
кая индукция
Магнитная
индукция
Плотность тока
6
7
Система уравнений максвелла.
Электродинамика покоящихся сред.
ДифференциаИнтегральная форма
льная форма


B
rotE  
t

  D
rotH  j 
t

divD  ρ

divB  0


D  ε 0 εE


B  μ 0μH


j  σE

 
B 
 Ed l   t dS
L
S
Вихревое
электрическое поле
порождается
изменением
магнитной индукции
и наоборот

 
D  Вихревое магнитное
Hd l  I encl 
dS поле порождается
t
электрическим
L
S
током и изменением
электрической
индукции
 
Электрический заряд
DdS  qencl
является источником
S
электростатического
поля
 
Магнитная индукция
BdS  0
не расходится
S
(магнитных зарядов
нет)
Связь электрической индукции с
напряженностью электростатического поля
Связь магнитной индукции с напряженностью
магнитного поля
Связь плотности тока с напряженностью
электростат. поля (Закон Ома в диф. форме)




B
  вектор индукции магнитного поля;
электрического поля;
E  вектор
 напряженности

D  ε 0 E  P  вектор электрического смещения;

 B 
H
 J  напряженности магнитного поля;
μ0

P
  поляризованность;
J  намагниченность вещества;
j  вектор плотности тока;
ρ  объемная плотность заряда.
Физический смысл
