Взаимодействие конического штампа с неоднородным основанием А.В. Чмшкян
реклама
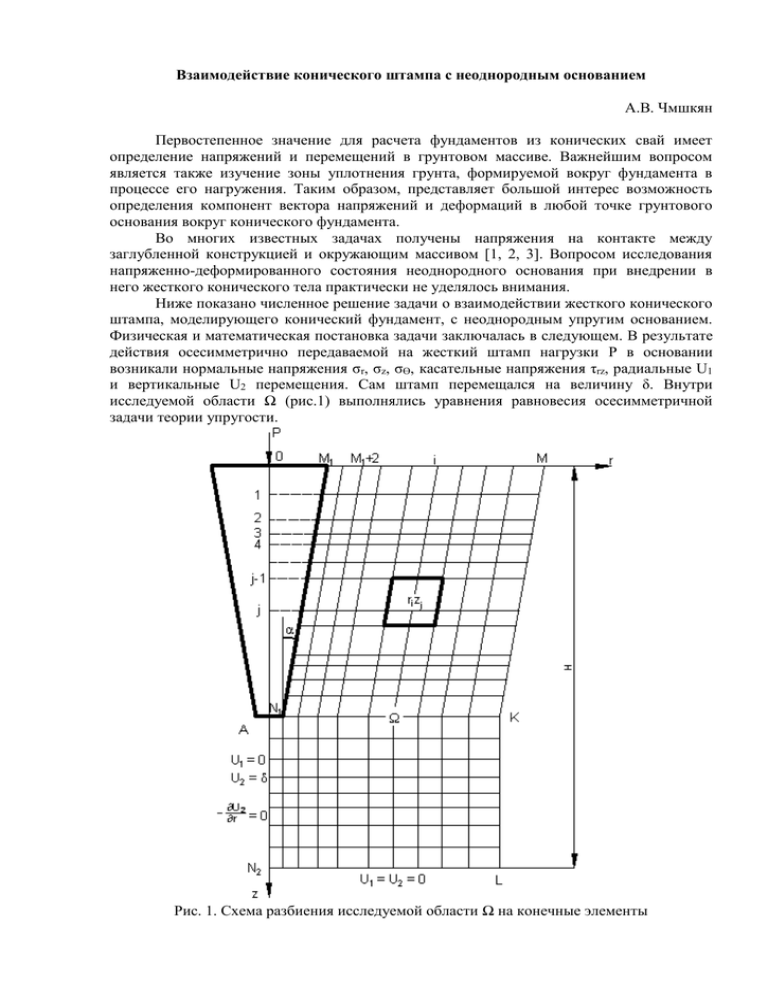
Взаимодействие конического штампа с неоднородным основанием А.В. Чмшкян Первостепенное значение для расчета фундаментов из конических свай имеет определение напряжений и перемещений в грунтовом массиве. Важнейшим вопросом является также изучение зоны уплотнения грунта, формируемой вокруг фундамента в процессе его нагружения. Таким образом, представляет большой интерес возможность определения компонент вектора напряжений и деформаций в любой точке грунтового основания вокруг конического фундамента. Во многих известных задачах получены напряжения на контакте между заглубленной конструкцией и окружающим массивом [1, 2, 3]. Вопросом исследования напряженно-деформированного состояния неоднородного основания при внедрении в него жесткого конического тела практически не уделялось внимания. Ниже показано численное решение задачи о взаимодействии жесткого конического штампа, моделирующего конический фундамент, с неоднородным упругим основанием. Физическая и математическая постановка задачи заключалась в следующем. В результате действия осесимметрично передаваемой на жесткий штамп нагрузки P в основании возникали нормальные напряжения σr, σz, σӨ, касательные напряжения τrz, радиальные U1 и вертикальные U2 перемещения. Сам штамп перемещался на величину δ. Внутри исследуемой области Ω (рис.1) выполнялись уравнения равновесия осесимметричной задачи теории упругости. Рис. 1. Схема разбиения исследуемой области Ω на конечные элементы На контуре граничные условия принимались следующими: σz = τrz = 0, при z = 0, r > R, то есть на поверхности вне штампа напряжения отсутствуют. По мере удаления в глубину и в стороны от штампа перемещения затухают U1 = U2 = 0, при z = H⋃(r,z) ∊ LKM. Так как грунт предполагается жестко скрепленным со сваей, то на ее боковой поверхности выполняются условия: U1 = 0, U2 = δ, при (r, z) ∊ ABM1. Под штампом вдоль оси Z выполняются условия симметрии: 𝜕𝑈 U1 = 0, 𝜕𝑟2 = 0, при r = 0. Решение проводилось в цилиндрической системе координат r, Ө, z методом конечных элементов (МКЭ) [4, 5]. Для построения решения исследуемая область была разбита на элементы в виде параллелограммов и прямоугольников (см. рис. 1). Неизвестными параметрами являлись радиальные U1 и вертикальные U2 перемещения узлов rizj, при пробегании индексами i и j всех значений i = 0, 1, 2, … , M1, … , M; j = 0, 1, 2, … , N1, … , N2. Внутри каждого элемента задано полилинейное распределение функций UK, K = 1, 2: UK = aKr + bKz + cKrz + dK, где aK, bK, cK, dK – постоянные коэффициенты, выраженные через перемещения (ℋ) соответствующих узлов на элементах ∆𝑖𝑗 , ℋ = 1, 2, 3, 4. Окончательно перемещения UK, (ℋ) K = 1, 2 на всем параллелограмме ∆𝑖𝑗 = ⋃4ℋ=1 ∆𝑖𝑗 представлены в виде 1 𝑈𝐾 = ∑ UK,i+m,j+n 𝜑𝑖+𝑚,𝑗+𝑛 (r, z) 𝜑𝑖+𝑛 (𝑧), 𝑚,𝑛=−1 где φi,j(r,z) и φj(z) – кусочно-полилинейные координатные функции. В силу принципа Лагранжа решение свелось к вариационной задаче о нахождении минимума функционала энергии J(𝑈1 , 𝑈2 ) = ∫ (𝜎𝑟 ε𝑟 + 𝜎𝜃 ε𝜃 + 𝜎𝑧 ε𝑧 + 𝜏𝑟𝑧 𝛾𝑟𝑧 )𝑟𝑑𝑠. Ω Входящие в функционал напряжения и деформации определялись из геометрических и физических уравнений теории упругости. В результате минимизации была получена система алгебраических уравнений для определения радиальных и вертикальных перемещений узловых точек области Ω. Решение системы проводилось методом верхней релаксации Un+1 = Un - τAUn, n где U – вектор столбец узловых перемещений; A – матрица коэффициентов; AUn – система алгебраических уравнений МКЭ; τ – итерационный параметр. По найденным перемещениям определялись компоненты вектора напряжений в узловых точках Ω и на контакте конического штампа с основанием. В результате интегрирования напряжений по поверхности штампа определялась сила, действующая на него. Для решения системы уравнений и вычисления напряжений составлена программа для ЭВМ. С помощью этой программы определены поля напряжений и перемещений в грунтовом основании конического фундамента при различных его геометрических параметрах и характеристиках окружающего грунта. Установлено, что изменение угла сбега образующих конического фундамента от 2º до 15º при постоянном его перемещении приводит к увеличению вертикальных напряжений, действующих на боковую поверхность на 20-25%. Изменение модуля общей деформации естественного грунта при постоянных значениях модулей в пределах уплотненной зоны практически не влияет на величину нагрузки, воспринимаемой фундаментом. Увеличение коэффициента Пуассона от 0,25 до 0, 4 незначительно (до 5%) влияет на напряженное состояние основания конического фундамента. Метод решения задачи позволил учесть неоднородность грунтового массива, которая обусловлена формированием уплотненной зоны в процессе погружения фундамента [6]. Так, при увеличении максимальной ширины зоны уплотнения с 2,0 до 2,5 D нагрузка, действующая на фундамент, возрастает в 1,3-1,5 раза, а изменение значений модулей общей деформации грунта внутри уплотненной зоны в 1,5 раза приводит к изменению нагрузки на фундамент на 25-30%. Литература 1. Златин А.Н., Уфлянд Я.С. Осесимметричная контактная задача о вдавливании упругого цилиндра в упругий слой. – Прикладная математика и механика, 40, 1976, №1. с. 79-84. 2. Ковнеристов Г.Б., Шишов О.В.Исследование распределения контактных напряжений для заглубленных штампов. – В кн.: Сопротивление материалов и теория сооружений. 1977, вып. 30, с. 44-47. 3. Стаин В.М. Напряжения в грунте в окрестности осесимметрично нагруженного жесткого фундамента. – В кн.: Труды Фрунзенского политехнического института. 1972, вып. 53, с. 29-33. 4. Ухов С.Б. Расчет сооружений и оснований методом конечных элементов. –М.: Издво МИСИ, 1973. -118с. 5. Винокуров Е.В. Итерационный метод расчета оснований и фундаментов с помощью ЭВМ. –Минск: Наука и техника, 1972. -246с. 6. Логутин В.В., Чмшкян А.В. О формировании зоны уплотнения вокруг конической сваи. – В кн.: Перспективные разработки проектирования и комплексное строительство сельскохозяйственных объектов на Северном Кавказе. – Ростов-наДону, 1984. с. 27-32.



