Уравнение Максвелла, оптическая часть спектра

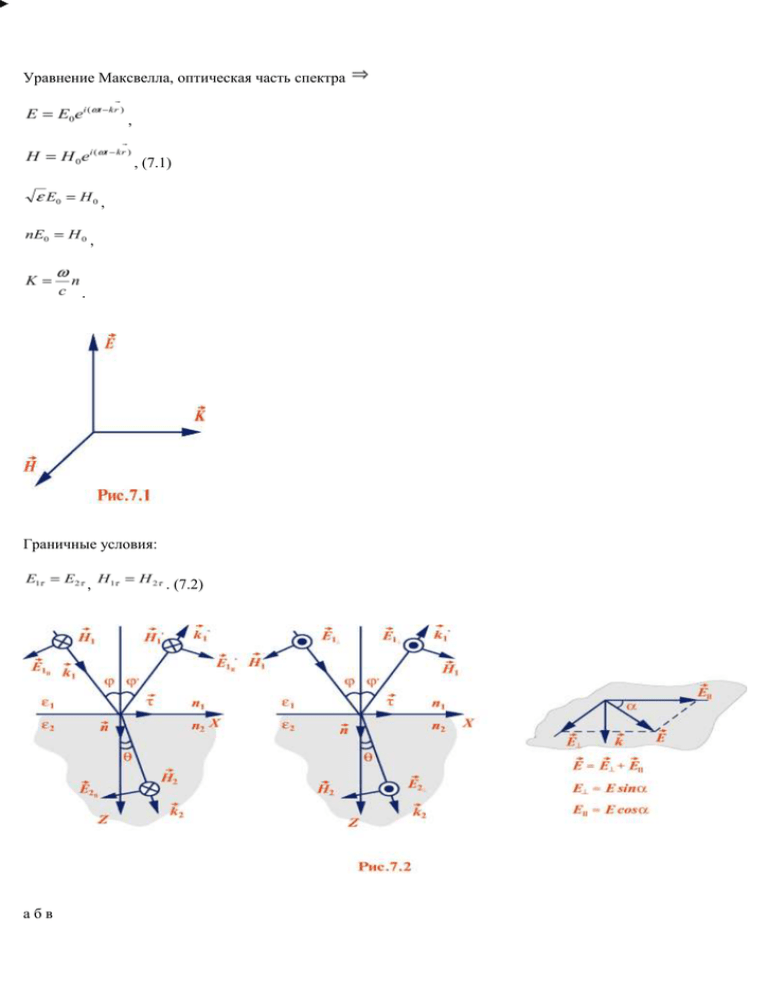
Уравнение Максвелла, оптическая часть спектра
,
, (7.1)
,
,
.
Граничные условия:
,
абв
. (7.2)
На
границе (плоскость ХY):
, (7.3)
,
.
Кинематические следствия:
1)
,
2)
;
, (7.4)
плоскости
.
Плоскость падения – плоскость образованная нормалью к границе раздела сред (ось
лучом (вектор ).
.
(7.5)
а) Пусть
, тогда (7.4)
Но
. (7.6)
. (7.7)
Отраженный и переломленный лучи лежат в плоскости падения.
б) Пусть
,тогда (7.4)
. (7.8)
; (7.9)
) и падающим
2.
. (7.10)
Закон преломления Снеллиуса.
, (7.11)
где
,
и
,
,
– соответственно фазовые скорости света в 1-ой и 2-ой среде.
,
,
. (7.12)
,
,
. (7.13)
Плоскую волну, вектор
которой произвольно ориентирован относительно плоскости падения (именно –
составляет угол с плоскостью падения) можно разложить на сумму волн, у одной из которых
напряженность электрического поля лежит в плоскости падения, а у другой перпендикулярно ей. Изучив
поведения этих волн при отражении и преломлении прямым применением принципа суперпозиции с
учетом аддитивности плотности потока энергии, получим все характеристики волны с произвольной
ориентировкой напряженности электрического поля.
Рис 7.2а, (7.2), (7.3)
(7.14)
def:
def:
рис. 7.2б, (7.2),(7.3)
, (7.15)
. (7.16)
(7.17)
def:
. (7.18)
def:
. (7.19)
- коэффициенты Френеля
def:
Замечание. Полученные соотношения (7.15),(7.16),(7.18),(7.19) и рис 7.4 соответствуют случаю
выбранному направлению векторов
и
на Рис. 7.2.
Отрицательные значения коэффициента
падения
направление векторов
рис. 7.2 направлению.
и
и
и
означают, что при соответствующих значениях угла
принимают направление противоположное показанному на
Следствие
1. При отражении от оптически более плотной среды (
(
и
) и углах падения (
) фаза обеих
) компонент электрического вектора противоположна фазе падающего (скачок фазы
совпадает с фазой падающей волны при
), и
. В частности, это имеет место и при нормальном падении
(
). Явление потери полуволны ( Δφ = π ) при отражении от оптически более плотной среды (
имеет важное значение в интерференционных установках.
2. При больших углах падения (
) и отражения от более плотной среды
и
противоположны по знаку, а
и
совпадают по фазе. Наоборот, при больших углах и (
и
и
противоположны по знаку.
совпадают по фазе, а
3. Преломленная волна во всех случаях (
фазу падающей волны.
4. При
5. При
(нормальное падение)
6. Особый случай:
и
,
) и при любых углах
,
(скользящее падение)
сдвиг фазы компонентов
случае.
падения
и
)
)
сохраняет без изменений
. (7.20)
, то есть происходит полное отражение света. При этом
определяется согласно пункту 2. Очевидно, что
,
в этом
, (7.21) что видно непосредственно из (7.15). Угол
, при котором обращается в нуль коэффициент Френеля
, называется углом Брюстера:
.
Отсюда
, (7.22)
При угле падения
:
, (7.23)
где n – относительный показатель преломления
, (7.24)
Примеры: стекло с
,
вода с
.
7. При падении света под углом Брюстера независимо от направления электрического вектора
отраженный пучок имеет направление колебаний только перпендикулярные плоскости падения. Иначе:
независимо от поляризации падающего пучка под углом Брюстера отраженный пучок поляризован
перпендикулярно плоскости падения.
8. Из формул Френеля следует, что компоненты
угла Брюстера (
и
совпадают по фазе, пока угол падения меньше
), и становиться противоположным по фазе, когда
при угле Брюстера происходит скачок фазы колебаний
на

Энергетические соотношения на границе раздела сред
Граница – плоскость
:
.
. Таким образом
, где
,
,
;
,
. (7.25.)
(7.26)
,
(7.27)
(7.28)
,
, (7.29)
.
Закон сохранения энергии:
Падающий на поверхность
поверхность
поток энергии
равен сумме потоков энергии отраженной и прошедшей через
,
. (7.30)
Введем коэффициенты отражения и прохождения:
(7.31)
и
Аналогично получим:
(7.32)
Напомним, что индекс
означает, что оба коэффициента
и
следует относить к падающей на
поверхность линейно поляризованной электромагнитной волне, при этом вектор
плоскостью падения угол .
составляет с
Для того, чтобы получить аналогичные соотношения для неполяризованной волны, достаточно полученные
выражения усреднить по всевозможным значениям в интервале
, т.е.
,
(7.33)
Упражнение: Проверить, что
, для этого достаточно убедиться, что
и
.
Неполяризованная волна после отражения становится частично поляризованной. Вычислим степень
поляризации отраженной волны:
(7.34)
Если отражается линейно поляризованная волна, то отраженная компонента остается линейно
поляризованной, однако вектор
составляет угол
с плоскостью падения, где
нетрудно вычислить:
(7.35)
Аналогичные соотношения нетрудно получить для преломленной компоненты.
Естественный и поляризованный свет.
Волна, в которой направление колебаний электрического вектора
каким-либо образом, называется поляризованной.
(а, значит, и
) упорядочено
Если колебания вектора
происходят в одной плоскости, проходящей через волновой вектор
, то говорят
о плоско-поляризованной волне (синоним – линейная поляризация). Плоскость, в которой колеблется вектор,
называют плоскостью поляризации. Если вектор
(а, значит, и
) вращается в плоскости,
перпендикулярной волновому вектору
с некоторой циклической частотой
, при этом конец вектора
описывает эллиптическую траекторию в каждой точке волновой поверхности (фронта) волны, то такую волну
называют эллиптически-поляризованной. Как частный случай, поляризованной по кругу (циркулярнополяризованной), если вектор
описывает окружность.
Вращение по эллипсу (кругу) может происходить в двух направлениях – в зависимости от направления
вращения вектора
различают правую и левую эллиптические (круговые) поляризации. Если наблюдатель
смотрит навстречу распространения волны, и вектор
при этом вращается по часовой стрелке (правый
винт), то поляризацию называют правой, в противном случае – левой.
Из рассмотренных видов поляризации – эллиптическая поляризация – наиболее общий вид поляризации
волны. Линейная поляризация и круговая могут рассматриваться как частный случай эллиптической.
Волну эллиптической поляризации можно разложить на две взаимно перпендикулярные линейнополяризованные волны с взаимно ортогональными плоскостями поляризации – разложить на два
ортогональных орта, совершающих гармонические колебания с постоянным сдвигом фазы (т.е. когерентные
друг другу). В зависимости от значений сдвига фазы
между колебаниями и соотношения между
амплитудами этих колебаний возникают разные виды эллиптических поляризаций (вспомним фигуры
Лиссажу в теории колебаний). При сдвиге фазы
,
получаем линейно-поляризованный свет.
Круговая поляризация возникает при сдвиге фаз
и равенстве амплитуд ортогональных колебаний.
Если же фазы хаотически меняются во времени – получаем некогерентное сложение ортогональных
колебаний одинаковой частоты. Такой свет носит название неполяризованного или естественного (см.
условное изображение на рис.7.8.в). Именно такой свет излучают естественные тепловые источники, в
которых громадное число некоррелированных, находящихся в хаотическом тепловом взаимодействии, атомов
излучают волновые цуги со случайными направлениями электрического вектора
, с фазой хаотически
меняющейся в каждом процессе излучения. Резюмируя вышесказанное, можно дать точное определение
естественного света.
Статистическая смесь плоско-поляризованных волн различных направлений вектора
, задаваемых
множеством разных углов
в плоскости фронта волны, при этом все направления вектора
равновероятны
.
Поляризаторы.
Как получить из естественного света плоско-поляризованный? Для этого существуют специальные
оптические приспособления – поляризаторы. Эти приборы свободно пропускают колебания, параллельные
плоскости, называемой плоскостью пропускания поляризатора. Колебания же, ортогональные этой плоскости,
задерживаются полностью.
Частично-поляризованный свет.
Частично-поляризованный свет можно представить в виде суперпозиции двух некогерентных плоскополяризованных волн с взаимно ортогональными плоскостями поляризации, но разными по
интенсивности, при этом
.
Частично–поляризованный свет можно интерпретировать как смесь в некоторой пропорции естественной
компоненты и плоско-поляризованной. На рис. 7.9 вертикальные колебания соответствуют максимальной
интенсивности
, горизонтальные – минимальной
. В качестве характеристики степени
поляризованности частично–поляризованного света вводится величина, называемая степенью поляризации
, которая определяется равенством:
. (7.34)
Очевидные соотношения:
,
– для естественного света, (7.35)
– для плоско-поляризованного света.
Замечание: Соотношения ( 7.34 ), (7.35) применимы только к смешанным состояниям и как предельный
случай к линейно-поляризованному свету. Эллиптическая поляризация как когерентная смесь не относится к
сфере применимости этих соотношений.
^ Закон Малюса. Пусть на поляризатор падает линейно-поляризованный свет, вектор
которого составляет
угол с плоскостью пропускания
. Вектор
направлен перпендикулярно плоскости поляризатора.
Поляризатор пропускает только ту составляющую вектора
, т.е.
, которая параллельна плоскости пропускания
. Поэтому интенсивность прошедшего света:
, (7.36)
где
– интенсивность падающего линейно-поляризованного света.
При этом прошедший пучок будет иметь поляризацию, т.е. вектор
пропускания поляризатора
.
, направленную вдоль плоскости
Поляризация света при прохождении через границу двух диэлектриков.
Формулы Френеля дают возможность рассчитать амплитуду каждой из компонент
и
в отраженном и в
проходящем свете, поэтому они содержат полное решение задачи о степени поляризации отраженного и
преломленного света.
Если свет естественный, то
. Для отраженного света, однако
, поэтому отраженный свет
становится частично-поляризованным. Так как
, то электрический вектор, перпендикулярный к
плоскости падения имеет большую амплитуду. При этом степень поляризации:
. (7.37)
Если
, то
;
и
, т.е. отраженный свет полностью поляризован, причем вектор
поляризации Ē1 перпендикулярен к плоскости падения. Коэффициенты Френеля
'
нуль и
, т.е.
и
и
не обращаются в
. Это означает, что имеет место частичная поляризация, причем
преимущество имеют колебания в плоскости падения. Если
.
При n=1,5 (воздух – стекло) → Р=
Вывод: проходящий свет частично поляризован (
.
)
Замечание.
При прохождении стеклянной плоскопараллельной пластинки на второй поверхности степень поляризации
еще увеличится на 0,08.