Выпуклая оболочка

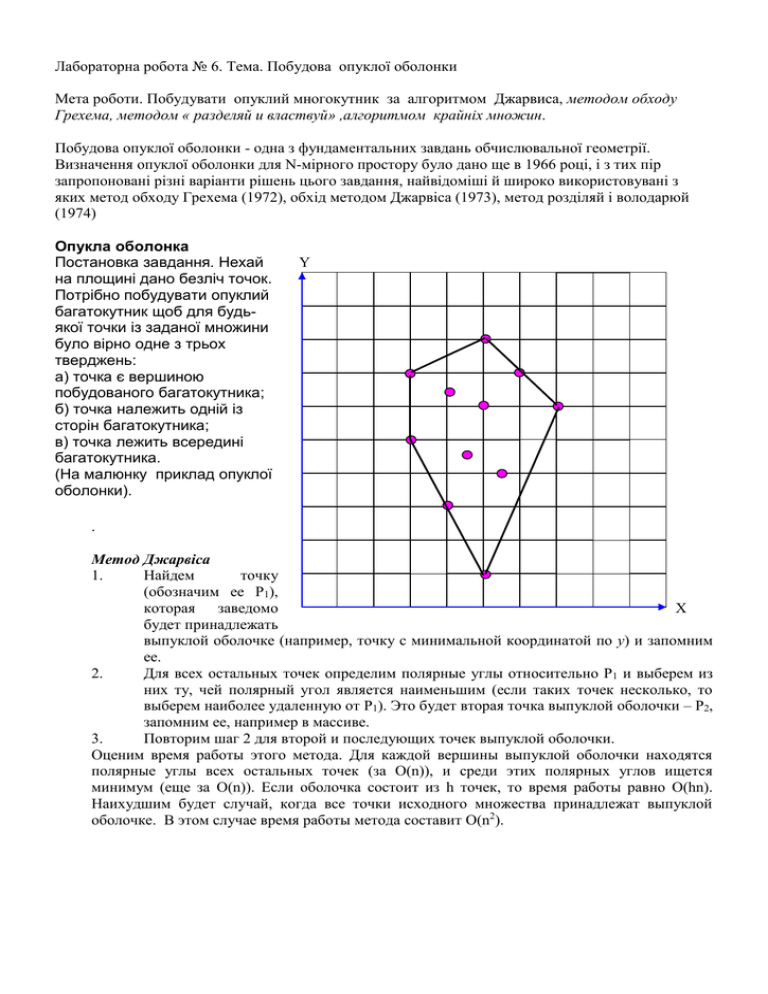
Лабораторна робота № 6. Тема. Побудова опуклої оболонки
Мета роботи. Побудувати опуклий многокутник за алгоритмом Джарвиса, методом обходу
Грехема, методом « разделяй и властвуй» ,алгоритмом крайніх множин.
Побудова опуклої оболонки - одна з фундаментальних завдань обчислювальної геометрії.
Визначення опуклої оболонки для N-мірного простору було дано ще в 1966 році, і з тих пір
запропоновані різні варіанти рішень цього завдання, найвідоміші й широко використовувані з
яких метод обходу Грехема (1972), обхід методом Джарвіса (1973), метод розділяй і володарюй
(1974)
Опукла оболонка
Постановка завдання. Нехай
на площині дано безліч точок.
Потрібно побудувати опуклий
багатокутник щоб для будьякої точки із заданої множини
було вірно одне з трьох
тверджень:
а) точка є вершиною
побудованого багатокутника;
б) точка належить одній із
сторін багатокутника;
в) точка лежить всередині
багатокутника.
(На малюнку приклад опуклої
оболонки).
Y
.
Метод Джарвіса
1.
Найдем
точку
(обозначим ее P1),
которая заведомо
X
будет принадлежать
выпуклой оболочке (например, точку с минимальной координатой по y) и запомним
ее.
2.
Для всех остальных точек определим полярные углы относительно P1 и выберем из
них ту, чей полярный угол является наименьшим (если таких точек несколько, то
выберем наиболее удаленную от P1). Это будет вторая точка выпуклой оболочки – P2,
запомним ее, например в массиве.
3.
Повторим шаг 2 для второй и последующих точек выпуклой оболочки.
Оценим время работы этого метода. Для каждой вершины выпуклой оболочки находятся
полярные углы всех остальных точек (за O(n)), и среди этих полярных углов ищется
минимум (еще за O(n)). Если оболочка состоит из h точек, то время работы равно O(hn).
Наихудшим будет случай, когда все точки исходного множества принадлежат выпуклой
оболочке. В этом случае время работы метода составит O(n2).
Зачастую в большинстве олимпиадных задач ставится дополнительное условие: «никакие
три точки» из множества не
лежат на одной прямой. В этом Y
случае сравнение по расстоянию
(и что самое главное, вычисление
этого расстояния) можно не
делать.
Также
необходимо
обратить внимание учащихся на
возможность
«вырожденного
случая», когда в исходном
наборе всего одна или две точки,
P3
или все точки исходного набора
лежат на одной прямой. В таких
частных случаях построение
выпуклой оболочки попросту
невозможно, что требует, с
P2
другой
стороны,
особой
аккуратности
при
формулировании задач, чтобы
учащиеся не тратили время на
P1
обработку частных случаев,
которые не предусматривались
автором данной задачи.
X
Метод Грэхема
1.
Найдем точку (назовем ее P1), заведомо принадлежащую выпуклой оболочке
(например, точку с минимальной координатой по y).
2.
Отсортируем все остальные точки по возрастанию
6
полярного угла относительно P1, в случае равенства
4
полярных углов – по возрастанию расстояния до нее
5
(полученный порядок обхода точек показан на рисунке;
красным цветом показан
луч, от
которого
3
отсчитываются полярные углы).
7
3.
Для всех отсортированных точек выполним обход
2
Грэхема. Пусть уже построена некоторая часть
P1
выпуклой оболочки. Тогда:
a. если на следующем шаге поворот делается против
часовой стрелки (что можно выяснить с помощью
свойства векторного произведения), то следующая
6
точка включается в оболочку (например, если первая
4
и вторая точки включены в выпуклую оболочку, и
5
рассматривается третья, то на этом этапе она должна
быть также включена, так как поворот от 2-й к 3-й
3
делается против часовой стрелки; синим цветом на
7
рисунке показаны стороны, которые принадлежат
2
выпуклой оболочке на данном шаге);
P1
b. если в следующем шаге поворота не делается, то
последняя добавленная точка исключается из выпуклой оболочки и добавляется
новая (так, при рассмотрении точки 4 необходимо исключить из оболочки точку 3,
и поставить новую точку вместо нее).
4.
c. если на следующем шаге делается поворот по
часовой стрелке, то последняя (или даже несколько)
6
точек исключается из выпуклой оболочки и вместо
4
5
них добавляется новая (так, при рассмотрении точки
6 оказывается, что от точки 5 к ней делается поворот
3
по часовой стрелке; в этом случае точка 5
исключается из выпуклой оболочки; фиолетовым
7
2
цветом показаны исключенные отрезки).
Процесс продолжается, пока все точки не будут
P1
обработаны. Также необходимо проверить поворот от
последней точке к P1 и при необходимости исключить несколько точек в конце
оболочки.
Алгоритм крайних множеств.
Все обозначенные алгоритмы поддаются машинной реализации, однако изначально
не могли учитывать её особенности и их эффективность значительно падает с
увеличением количества точек. Алгоритм построения выпуклой оболочки для
множества точек плоскости, в котором используются специфические преимущества
реализации алгоритма на машинных языках, благодаря чему достигается более
высокая эффективность его применения для обсчёта множеств, характеризующихся
высокими мощностями – алгоритм крайних множеств.
Постановка задачи. Пусть на плоскости задано множество n точек,
определяющихся массивами декартовых координат. Необходимо найти точки,
принадлежащие выпуклой оболочке для данного множества точек.
Шаг 1. Массив с координатами точек сортируется по оси абсцисс и ординат
рекуррентным методом быстрой сортировки [2].
Шаг 2. После сортировки известны координаты крайних по оси абсцисс точек
(точки с наименьшей и наибольшей абсциссой). Сортировка по оси ординат
обеспечивает определение наивысшей и наинизшей точек при заданном значении x.
При передвижении слева направо по абсциссам заданных точек определяются
наивысшая и наинизшая точки, образующие два множества: «верхнее» и «нижнее».
Если при очередном значении x имеется только одна точка, она считается
принадлежащей обоим множествам. Таким образом, полученные множества будут
упорядоченными по значениям абсцисс (рис. 1).
Рис. 1. Выделение верхнего и нижнего
подмножеств.
Рис. 2. Удаление лишних точек из
подмножеств.
Рис. 3. Устранение заломов, искомая выпуклая оболочка.
5.
6.
7.
Шаг 3. Действия над «верхним» и «нижним» множествами идентичны, поэтому
рассмотрим операции над «верхним» множеством. При перемещении по оси абсцисс
от первой точки массива до наивысшей отбрасываются точки, ордината которых
меньше ординаты предыдущей точки (выполняются простейшие операции
сравнения). Аналогично производится перемещение от последней точки до
наивысшей (рис. 2). Иногда этих операций уже достаточно для получения контура
выпуклого многоугольника.
Шаг 4. Ликвидация «заломов». Проверяется, находится ли средняя точка из трёх
подряд идущих точек «выше» прямой, образованной двумя другими точками (для
«нижнего» множества – «ниже»): на данной прямой находится точка с абсциссой,
равной абсциссе средней точки; если её ордината меньше (для «нижнего» множества
– больше) ординаты средней точки, то точка исключается. Таким образом, получаем
верхнюю и нижнюю части выпуклого многоугольника (рис. 3). Осталось их
соединить.
Последний шаг можно было применить сразу после второго, но на четвёртом шаге
происходит больший расход процессорного времени (операция расчёта координаты
точки, лежащей на прямой, и операция сравнения), чем на третьем шаге (только
операция сравнения). Поэтому «быстрый» отсев точек на третьем шаге значительно
ускоряет заключительную проверку на выпуклость.