11-1 - RTU DF

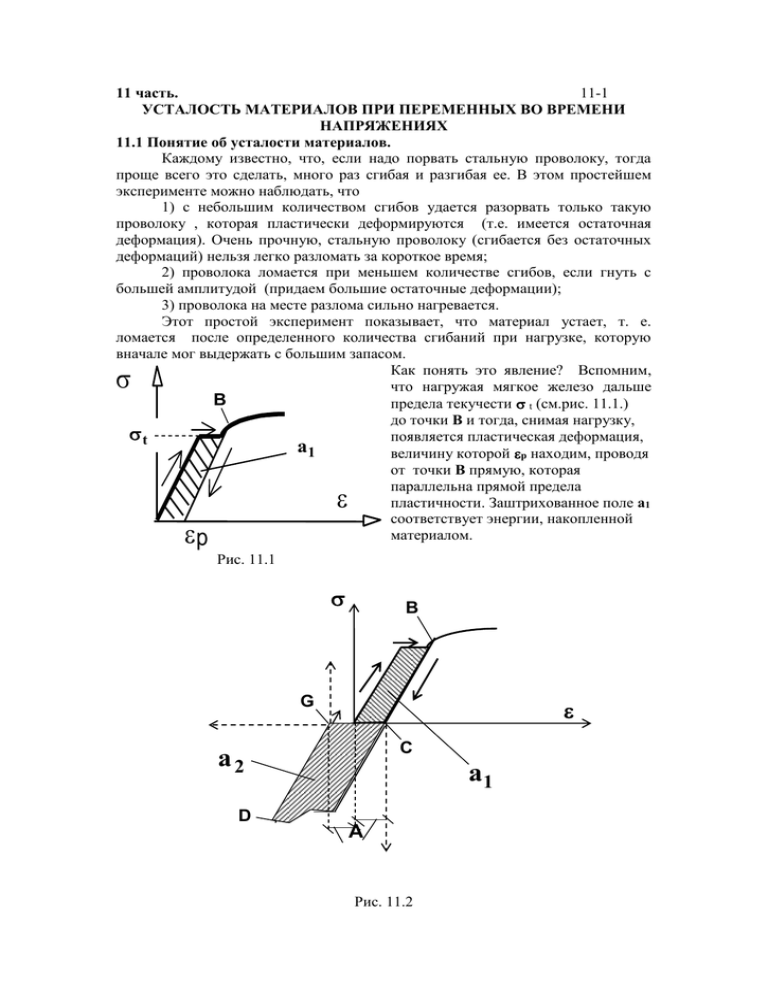
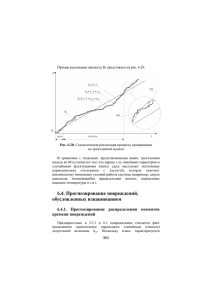
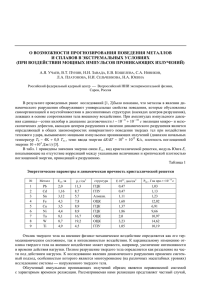
11 часть.
11-1
УСТАЛОСТЬ МАТЕРИАЛОВ ПРИ ПЕРЕМЕННЫХ ВО ВРЕМЕНИ
НАПРЯЖЕНИЯХ
11.1 Понятие об усталости материалов.
Каждому известно, что, если надо порвать стальную проволоку, тогда
проще всего это сделать, много раз сгибая и разгибая ее. В этом простейшем
эксперименте можно наблюдать, что
1) с небольшим количеством сгибов удается разорвать только такую
проволоку , которая пластически деформируются (т.е. имеется остаточная
деформация). Очень прочную, стальную проволоку (сгибается без остаточных
деформаций) нельзя легко разломать за короткое время;
2) проволока ломается при меньшем количестве сгибов, если гнуть с
большей амплитудой (придаем большие остаточные деформации);
3) проволока на месте разлома сильно нагревается.
Этот простой эксперимент показывает, что материал устает, т. е.
ломается после определенного количества сгибаний при нагрузке, которую
вначале мог выдержать с большим запасом.
Как понять это явление? Вспомним,
что нагружая мягкое железо дальше
B
предела текучести  t (см.рис. 11.1.)
до точки В и тогда, снимая нагрузку,
t
появляется пластическая деформация,
a1
величину которой p находим, проводя
от точки В прямую, которая
параллельна прямой предела
пластичности. Заштрихованное поле a1
соответствует энергии, накопленной
материалом.


p
Рис. 11.1

B
G

C
a2
D
a1
A
Рис. 11.2
11-2
Так как на осях отложены не перемещение и сила (которая дает энергию всему
образцу), а  (сила на единицу площади) и  (см на см), тогда мы получаем
энергию, которая накапливается на один см3
kN cm Ncm
.

(
)
2
3
cm
cm
cm
Если проволоку сгибают в обе стороны с одинаковой амплитудой А, (см.
рис. 11.2, заштрихованная площадь показываетнакопленную энергию
материала). тогда рассеяние энергии еще больше. В точке С помещаем как бы
повернутую диаграмму  . В точке D значение A со знаком минус. В точке G
опять помещаем новую диаграмму  и т.д. Видно, что площадь между
точками С и D и G, которую отсекает кривая, намного больше односторонней
нагрузки и разгрузки. А это значит что можно передать больше энергии
материалу.Всю внесенную энергию получим суммируя все составляющие
энергии
r n
a   ar
r 1
Где остается энергия в материале? Мы уже наблюдали, что материал
нагревается, часть энергии в виде тепла выделяется в атмосферу, а большая
часть энергии используется для преобразования структуры материала, т. е. для
его разрушения. Для пластичного материала происходит сдвиг кристаллов и
постепенное разрушение связей.
Похожая картина наблюдается тогда, когда нагружаем хрупкий материал
или пластичный на границе пластичности. Очень точно выполняя кривую
нагрузки и разгрузки (с точностью   10-10), видно, что в этих пределах
образуется небольшая кривая (с точностью  10-10) , которую мы не учитывали,
потому что нам не требовалась столь высокая точность при расчетах. Понятно,
что столь малым площадям петли соответствуют очень маленькие энергии в
цикле. Чтобы собрать достаточную энергию для разрушения, надо большое
число циклов n.
Переменные напряжения во времени больше всего наблюдаются при изгибе,
например, на железнодорожных рельсах, в межэтажных покрытиях под
колеблющимися приборами, и т. д. Ось колесной пары R, которая нагружена
весом Q, показана на рис. 11.3. В нижней точке оси A существуют напряжения
растяжения. При повороте оси на 900, точка A оказывается в положении 1 (см.
рис.11.3b)и там напряжений растяжения нет. При повороте оси еще на 90 0,
точка A оказывается в положении 2, где действуют напряжения сжатия.Это
означает, что в каждой точке поверхности колесной пары напряжения меняются
во времени, что показано на рис. 11.d. Как видим, этот процесс такой же, как и
когда мы сгибаем проволоку, чтобы сломать ее напополам.
11-3
2
Q
R
1
A
Рис. 11.3 a

Рис.11.3b
A
B
A
1
t
2
Рис.11.3c
Рис.11.3d
Ось колесной пары или любой другой стержень и балка, которые
нагружены переменной во времени нагрузкой, начинают разрушаться с
микротрещины на поверхности. Она является концентратором напряжений. На
кромке микротрещины возникают очень большие напряжения, и трещина
расширяется немного дальше. В последующем цикле еще дальше и т.д.
Локально в этом месте материал разрушается быстрее, и микротрещина
становится трещиной. Такой рост трещины продолжается до тех пор, пока
остальной еще неразрушенный материал (зона A рис.11.3c) может
воспринимать нагрузку статически, т.е. нагружаться один раз. Когда
неразрушенное сечение становится достаточно мало, чтобы воспринять
статическую нагрузку, деталь ломается.
Место усталостного излома является очень характерным. В свежем месте
разлома видна зернистая структура материала (зона A), а грани трещины в
циклическом процессе стерлись и блестят, как отполированная поверхность
(зона B), поэтому усталостный излом можно легко отличить от излома при
слишком большой статической нагрузке.
11.2 Кривая Велера.
Так как в эксперименте усталости влияние косвенных факторов очень
большое (больше чем при проверке растяжения определяя B ), то на каждую
точку эксперимента надо брать минимум 6...10 одинаковых образцов с
одинаковой нагрузкой.
Серию экспериментов проводят так. Первую экспериментальную точку
(для 6...10 образцов) получают, нагружая так, чтобы амплитудное значение 1
было немного меньше B (рис. 11.4).

1
2
-1
n1 n2
10
7
n
11-4
Нагружают так долго, пока образец
ломается, и фиксируют соответствующее
количество циклов n1. Так как скорость
нагружения не влияет на усталость, а
только количество энергии, т.е., число
циклов, это тоже фиксируем.
В следующей экспериментальной точке еще
уменьшаем 2 и находим n2 и т. д.
Рис.11.4
Так поступаем до тех пор, пока достигаем напряжение, при котором образец не
разрушается. Обычно считают, что граница достигнута если образец выдержал
107 циклов. Ей соответствующую амплитуду напряжения называют пределом
долговечности и обозначают -1, а всю полученную кривую кривой Велера.
Чтобы понять, как важно знать предел долговечности -1,
охарактеризуем ее таким экспериментальным соотношением для стали
-1  (0,4 ...0,6 ) B
11.3 Влияние разных факторов на предел долговечности.
Детали от экспериментальных образцов отличаются как по величине, так
и по форме и по механической обработке. Все эти факторы очень влияют на
предел долговечности -1. В практических расчетах для этой цели вводят
дополнительные коэффициенты и предел долговечности элемента конструкции
-1e получают, деля предел долговечности r на разные коэффициенты ek, т. е.
e1 
 1
emek e v
Значения коэффициентов ek можно найти в специальной литературе, но
здесь мы рассмотрим только причины их возникновения.
11.3.1 Масштабный коэффициент.
Чем больше деталь, тем больше вероятность, что в какой-то точке будет
малая прочность. Изготавливая маленькие образцы из большого образца, только
в одном из них будет эта малая прочность, а в остальных она будет больше.
Вместе с тем долговечность маленьких образцов будет больше, чем у большого
(см.рис.11.5). У длинного образца в слабом месте предельным усталостным
напряжением будет  B . Предположим , что мы разделили этот длинный
стержень на n частей и каждую часть проверим на растяжение. У каждого
r
отдельного r-го образца будет свой  B . И только у одного образца (в котором
находится слабое место) это напряжение совпадет с длинным образцом  B .
11-5
У остальных будет больше. Обрабатывая математически результат
экспериментов с маленькими образцами, получаем
1 n
 B    rB Tā kā  rB   B tad dabīgi, ka  B   B
n r 1
Зная вероятность дефектов, масштабный коэффициент em можно
определить и теоретически, но, так как распределение дефектов является
экспериментальным, то масштабный коэффициент обычно табулирован по
результатам экспериментов.
L
B
em
r
1
L
Рис.11.5
11.3.2 Коэффициент концентрации напряжений.
Гипотеза плоских сечений и вместе с тем, найденные в предыдущих
разделах, распределения напряжений подходят только для гладких, длинных
стержней с постоянной площадью поперечного сечения на достаточном
расстоянии от мест крепления. Если эти условия не выполняются, то надо
использовать более сложную теорию - теорию непрерывной среды. Так на рис.
11.6 показано распределение напряжений для стержня с отверстием по гипотезе
11-6
F
ek 
 max

r

ek
max
1
r
F
Рис.11.6a
Рис.11.6b
плоских сечений (в части стержня, где нет отверстия) и фактическое
распределение напряжений в поперечном сечении, где находится отверстие.
Видно, что фактические напряжения в месте их концентрации могут быть
намного больше тех, которые находим по формулам теории стержней. Поэтому
надо напряжение , определенное по теории стержня, сравнивать с
коэффициентом концентрации напряжений e k и тогда сравнивать с пределом
долговечности т. е.
ek   1
На рис.11.6b показана ось зубчатых колес с постепенным изменением диаметра.
На графике показан коэффициент концентрации напряжений e k в зависимости
от радиуса закругления r места сопряжения.
Следует заметить что, вычисляя коэффициенты концентрации напряжений с
помощью моделей непрерывной среды, расчет часто упрощают, принимая, что
материал остается пластичным до самого момента разрушения. Это бывает
оправдано для хрупких материалов.
2
2


1



A
Рис.11.7

11-7
Для пластических материалов (см.рис.11.7) за пределом текучести при том же 
(той же амплитуде сгибания А)фактическое напряжение (точка 1 рис. 11.7)
меньше, чем то, которое найдено, принимая, что материал пластичен до
разрушения (точка 2).
11.3.3 Влияние обработки поверхности.
При механической обработке поверхностей (фрезеровании, точении,
шлифовке) режущий инструмент отрывает часть материала и в материале
остается ямка, которая может стать началом трещины, которая может стать
началом трещины. Это и является локальным концентратором напряжений.
Масштаб этого дефекта слишком маленький, чтобы его рассчитать даже с
помощью точных моделей и компьютерных программ. Поэтому в наше время
влияние обработки поверхности можем определить только экспериментально.
Для оценки этого дефекта отметим только то, что после шлифования,
обрабатывая деталь с помощью струи чугунных шариков, предел долговечности
можно увеличить многократно.
На рис.11.8 показано, как струей шариков обрабатываются неровности
поверхности.
ev
1
h
Рис. 11.8
В правой части рисунка показана зависимость коэффициента обработки
поверхности от высоты неровности поверхности h.
Вопросы для проверки:
1). Что такое усталость материала?
2). Почему материал разрушается от многократного сгибания?
3). Как в пластичном материале накапливается энергия и на что она
расходуется?
4). Кривая Веллера
5). Как можно отличить усталостное разрушение от простого разрушения под
нагрузкой?
6). Что такое предел долговечности (усталостной прочности)?
7). Как учитывается влияние различных факторов на предел усталостной
прочности?
8). Что такое масштабный коэффициент?
9). Что такое коэффициент концентрации напряжений?
10). Почему считается, что закаленная сталь хуже воспринимает переменные
во времени нагрузки?
11). Как обработка поверхности влияет на предел долговечности?