Сечения многогранников , проходящее через середины 1. Изобразите сечение единичного куба ребер

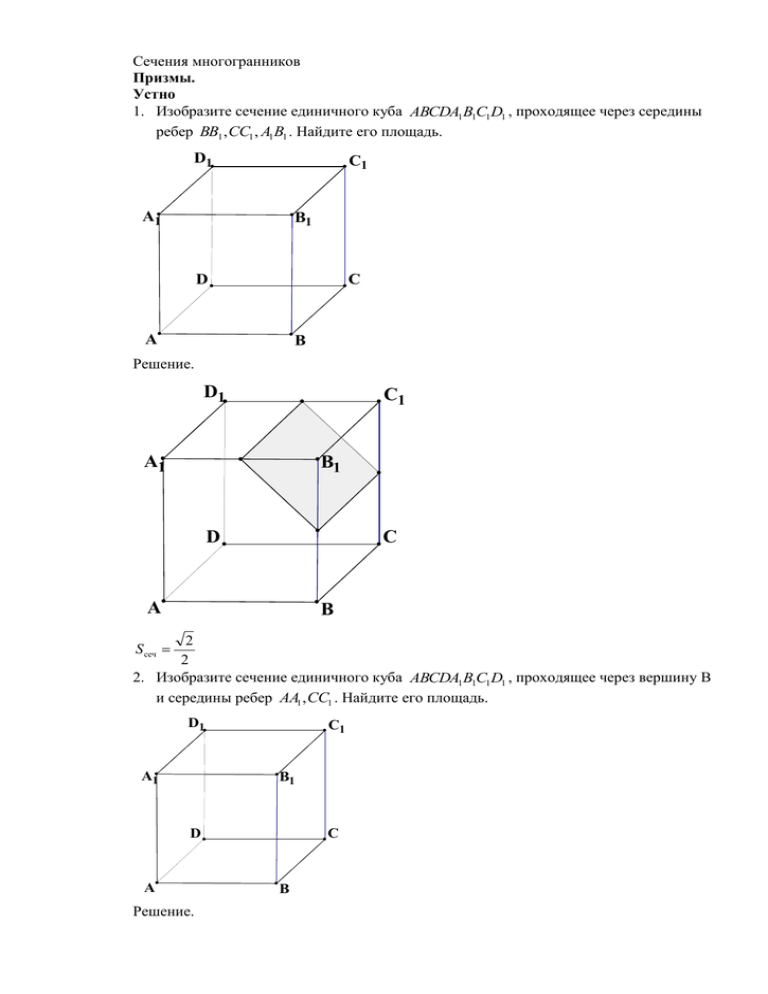
Сечения многогранников
Призмы.
Устно
1. Изобразите сечение единичного куба ABCDA1 B1C1 D1 , проходящее через середины
ребер BB1 , CC1 , A1 B1 . Найдите его площадь.
D1
C1
A1
B1
D
C
A
B
Решение.
D1
C1
A1
B1
D
C
A
B
2
2
2. Изобразите сечение единичного куба ABCDA1 B1C1 D1 , проходящее через вершину B
и середины ребер AA1 ,CC1 . Найдите его площадь.
S сеч 
D1
A1
C1
B1
D
A
Решение.
C
B
D1
C1
A1
B1
D
C
A
B
d1  d 2
Почему можно использовать эту формулу? Объясните.
2
d1  2 ; d 2  3 , почему?
S сеч 
6
2
3. Изобразите сечение единичного куба ABCDA1 B1C1 D1 , проходящее через вершины
A1 , B и середину ребра CC1 . Найдите его площадь.
S сеч 
D1
A1
C1
B1
D
A
C
B
Решение.
D1
A1
M
C1
B1
D
A
N
C
B
Объясните, почему искомое сечение A1MNB - равнобедренная трапеция?
Как найти площадь равнобедренной трапеции?
1
Объясните, почему ответ 1 .
8
Операционно-познавательная часть.
Знакомство с критериями.
Содержание критерия
Обоснованно получен верный ответ
Решение содержит обоснованный переход к планиметрической
задаче, но получен неверный ответ или решение не закончено, или
при правильном ответе решение недостаточно обоснованно
Решение не соответствует ни одному из критериев, перечисленных
выше
Максимальный балл
Баллы
2
1
0
2
1. ( МИОО 2013 г.) В правильной треугольной призме ABCA1 B1C1 стороны основания
равны 6, боковые ребра равны 4. Найдите площадь сечения, проходящего через
вершины A, B и середину ребра A1C1 .
C1
M
N
A1
B1
C
A
H
B
Решение.
M - середина ребра A1C1 , N - середина ребра B1C1 .
MNA1 B1AB .
AMNB - искомое сечение, равнобедренная трапеция.
AB  6, MN  3 .
AM  4 2  32  5 .
2
91
3
Высота трапеции MH  5    
.
2
2
2
S AMNB 
MN  AB
9 91 9 91
 MH  

.
2
2 2
4
2. Точка E – середина ребра AA1 куба ABCDA1B1C1D1. Найти площадь сечения куба
плоскостью C1DE, если ребра куба равны 2.
Решение.
D1
M
A1
P
C1
B1
E
C
D
A
B
Искомое сечение – равнобедренная трапеция EMC1D. Объясните почему?
E
2
M
5
5
D
C1
2
2
2 2
1
3

2
2
1
3
9
S сеч   3 2 
  4,5 .
2
2 2
3. (В.А. Смирнов) Изобразите сечение правильной шестиугольной призмы
ABCDEFA1 B1C1 D1 E1 F1 , проходящее через вершины A, C, D1 . Найдите его площадь.
h  5
E1
D1
F1
C1
A1
B1
E
D
F
C
A
Решение.
B
E1
D1
F1
C1
A1
B1
E
D
F
C
A
B
ACD1 F1 - искомое сечение. Объясните почему?
ACD1 F1 - прямоугольник. Объясните почему?
Sсеч  6 .
4. (ЕГЭ,
сибирь,
2013)
В
правильной
четырехугольной
призме
ABCDA1 B1C1 D1 сторона основания равна 20, боковое ребро AA1  7 . Точка
M принадлежит ребру A1 D1 и делит его в отношении 2:3, считая от вершины D1 .
Найдите площадь сечения этой призмы плоскостью, проходящей через точки B, D, M .
D1
C1
A1
B1
D
C
A
B
Решение.
M
D1
C1
N
A1
B1
D
A
C
B
MNBD
DMNB - равнобедренная трапеция. Почему?
3
BD  20 2 , MN  BD , MN  12 2
5
BN  7 2  82  113
 
2
h  113  4 2  9
1
S сеч  20 2  12 2  9  16 2  9  144 2
2
5. Изобразите сечение многогранника, изображенного на рисунке, все двугранные углы
которого прямые, проходящее через вершины A, C и A2 . Найдите его площадь.


D2
1
C2
2
1
B2
A2
2
A1
D
A
D1
B1
C1
C
B
2
Решение.
D2
1
C2
2
A2
S=3 2
1
B2
2
A1
D
A
2
D1
B1
C1
C
B
Домашнее задание.
1. Изобразите сечение единичного куба ABCDA1 B1C1 D1 , проходящее через вершину D1
и середины ребер AB, BC . Найдите его площадь.
D1
A1
C1
B1
D
A
Решение.
C
B
D1
C1
A1
B1
K
D
C
L
N
A
B
M
P
Ответ:
7 17
24
2. Дан куб ABCDA1B1C1D1. Через точки A,B1 и середину ребра CC1 проведена
секущая плоскость. Найдите площадь полной поверхности куба, если S сеч  36 .
Решение.
D1
A1
C1
K
B1
P
D
C
N
A
B
Пусть сторона куба x . Тогда S пол  6x 2 .
Сечение – равнобедренная трапеция AB1KN/
x
2
N
K
5x
2
A
h
5
B1
2x
4
x 2
5 2 1 2
3
x  x 
x
4
8
2 2
1 3 2
3
S сеч  
x
x  36 ; x 2  32
2 2
2 2
S пол  6  32  192
3. В прямоугольном параллелепипеде ABCDA1 B1C1 D1 известны ребра AB  8 ,
AD  7 , AA1  5 . Точка W принадлежит ребру DD1 и делит его в отношении 1:4,
считая от вершины D . Найдите площадь сечения этого параллелепипеда плоскостью,
проходящей через точки C,W , A1 .
D1
C1
A1
B1
D
C
A
B
Решение.
D1
C1
A1
B1
K
W
D
A
C
B
A1 K  82  12  65 ; WC  65
KC  A1W  7 2  4 2  65
4. Изобразите сечение многогранника, изображенного на рисунке, все двугранные
углы которого прямые, проходящее через вершины A, B и C1 . Найдите его
площадь.
D1
4
A3
A1
D3 1
C1
C3
B3
4
A
3
B1
D
2
C
C2
D2
1 A2 B2
1
B
Решение.
D1
A1
S=10 2
4
4
A3
D3 1
B1
D
2
A
B2
2
1
C1
C3
B3
D2
A
3
C
C2
1
B
Пирамиды.
Устно
1.В правильной треугольной пирамиде SABC ребра BA и BC разделены точками K и
L соответственно, в отношении 2:1, считая от вершины B (см. рисунок) Найдите угол
между плоскостью основания ABC и плоскостью сечения SKL . Ответ выразите в
градусах. Ответ: 90
S
C
A
L
K
B
2.Изобразите сечение единичного тетраэдра ABCD , проходящее через середины ребер
AD, BD и BC . Найдите его площадь.
D
C
A
B
Решение.
D
M
N
C
A
P
L
B
Объясните, почему MNLP - прямоугольник? S сеч  0,25
3. Найдите площадь треугольника, вершинами которого являются вершины
S , B, D правильной четырехугольной пирамиды SABCD с ребрами, равными 1.
S
D
C
A
B
Решение.
S
D
C
A
B
SDB - искомое сечение.
2
DB  2 , h 
2
1
2
S сеч   2 
 0,5
2
2
4. Изобразите сечение правильной четырехугольной пирамиды SABCD , проходящее
через вершины A, B и середину ребра SC . Все ребра пирамиды равны 1. Найдите его
площадь.
S
D
A
Решение.
C
B
S
M
N
D
C
A
B
ABMN - искомое сечение, так как MNCDAB .
ABMN - равнобедренная трапеция.
1
AB  1, MN  .
2
2
3
AM 
; h
2
 3   1 2
11


 2    4   4 .


1  1  11 3 11
S сеч  1   

2 2 4
16
Операционно-познавательная часть.
1. (ЕГЭ 2013 г.) В правильной четырехугольной пирамиде MABCD с вершиной
M стороны основания равны 6, а боковые ребра равны 12. Найдите площадь сечения
пирамиды плоскостью, проходящей через точку C и середину ребра MA параллельно
прямой BD .
Решение.
M
E
G
P
D
F
A
O
C
B
Пусть точка E - середина ребра MA . Отрезок CE пересекает плоскость MBD в точке
P . В треугольнике MAC точка P является точкой пересечения медиан, следовательно,
MP : PO  2 :1 . Отрезок FG параллелен BD и проходит через точку P (точка
F принадлежит ребру MB , G ребру MD ).
CE  FG
Четырехугольник CFEG - искомое сечение. CE  FG . S CFEG 
.
2
CE - медиана треугольника MAC .
2 AC 2  2MC 2  MA 2
CE 
2
 
2
2  6 2  2 12 2  12 2
2  72  144
CE 

6 2
2
2
2
2
FG  BD , FG   6 2  4 2 .
3
3
6 2 4 2
S CFEG 
 24 .
2
2. В правильной четырехугольной пирамиде SABCD с основанием ABCD проведено
сечение через середины ребер AB и BC и вершину S . Найдите площадь этого
сечения, если боковое ребро пирамиды равно 5, а сторона основания равна 4.
Решение.
S
D
C
P
A
K
M
B
Искомое сечение – треугольник SKM .
1
1
KM  AC   4 2  2 2 .
2
2
Проведем в треугольнике SKM высоту
1
KP  KM  2 .
2
SP , где
P - середина
KM . Значит,
Из прямоугольного треугольника SKA находим SK  SA2  AK 2  25  4  21 .
Из прямоугольного треугольника SPK находим SP  SK 2  KP 2  21  2  19 .
1
1
Тогда S SKM  KM  SP   2 2  19  38 .
2
2
3. В правильной треугольной пирамиде DАВС с вершиной D высота равна 3, а боковые
ребра равны 6. Найдите площадь сечения этой пирамиды плоскостью, проходящей через
середины сторон АВ и АС параллельно прямой DА.
D
P
K
N
A
C
M
B
Решение.
Почему MKPN - искомое сечение?
1. AB=9
9
2. MN 
2
3. MK  3
27
4. S сеч 
Объясните каждый этап решения.
2
Домашнее задание.
1. В правильной четырехугольной пирамиде SABCD с вершиной S известны ребра
AB  1, SD  2. Точка M - середина ребра SC . Найдите площадь сечения этой
15 2
.
32
2. В правильной треугольной пирамиде SABC с основанием ABC проведено сечение
через середины ребер AB и BC и вершину S . Найдите площадь этого сечения,
если боковое ребро пирамиды равно 7, а сторона основания равна 8. Ответ: 2 29 .
3. В правильной треугольной пирамиде SABC с основанием ABC сторона основания
равна 8, а угол ASB  36 0 . На ребре SC взята точка M так, что AM - биссектриса
угла SAC . Найти площадь сечения пирамиды, проходящей через точки A, M , B .
пирамиды, проходящего через точки M , A, D. Ответ:
Подсказка: сечение – равносторонний треугольник. Ответ: 16 3 .
Тела вращения.
Устно
1. В цилиндрический сосуд налили 3000 см3 воды. Уровень воды при этом достиг высоты
20 см. В жидкость полностью погрузили деталь. При этом уровень жидкости в сосуде
поднялся на 3 см. Чему равен объем детали? Ответ выразите в кубических сантиметрах.
( V  S осн h ; S осн  150 ) Vдет  150  3  450 .
2.Цилиндр и конус имеют общее основание и общую высоту. Вычислите объем цилиндра,
если объем конуса равен 20. (60)
3. Объем конуса равен 32. Через середину высоты параллельно основанию конуса
проведено сечение, которое является основанием меньшего конуса с той же вершиной.
Найдите объем меньшего конуса. (4)
4.В сосуд, имеющий форму конуса, налили 30 мл жидкости до половины высоты сосуда.
Сколько миллилитров жидкости нужно долить в сосуд, чтобы заполнить его доверху?
(210)
Операционно-познавательная часть
1. Плоскость α пересекает два шара, имеющих общий центр. Площадь сечения меньшего
шара этой плоскостью равна 7. Плоскость β, параллельная плоскости α, касается меньшего
шара, а площадь сечения этой плоскостью большего шара равна 5. Найдите площадь
сечения большего шара плоскостью α.
Решение.
O1
A
B
O
C
O2
O1 A  r1 ; O2C  r2
r12  7 ; r2 2  5 . O1 B  ?
Заметим, что OO2  OA , а OC  OB .
Тогда по теореме Пифагора в OO1 A, OO1 B, OO2C получаем
O1 B 2  OB 2  OO1  OC 2  (OO2  r1 )  r2  r1
2
2
2
2
2
Sсеч  O1 B 2  r2  r1  5  7  12
2. Две параллельные плоскости, расстояние между которыми 2, пересекают шар. Одна из
плоскостей проходит через центр шара.
Отношение площадей сечений шара этими плоскостями равно 0,84. Найдите радиус шара
Решение.
OO1  2
2
O1
2
O
2
A
r
r
O1 A2
 0,84
r 2
O1 A2  0,84r 2
O1 A2  r 2  4
0,84r 2  r 2  4
0,16r 2  4
r 2  25
r 5
3. Радиус основания конуса равен 8, а его высота равна 15. Плоскость сечения содержит
вершину конуса и хорду основания, длина которой равна 14.
Найдите расстояние от центра основания конуса до плоскости сечения.
Решение.
B
H
O
A
OA  8, AB  14
Значит, AH  7 . Тогда OH  82  7 2  15 .
C
h
H
O
По условию, OC  15 .
OH  15 . Тогда HC  152  15  15 16  4 15
15
4 15  h  15 15 ; h  - искомое расстояние.
4
4. В правильную шестиугольную пирамиду, боковое ребро которой равно 5 , а высота
равна 1, вписана сфера. (Сфера касается всех граней пирамиды). Найдите площадь этой
сферы
5. Высота цилиндра равна 5, а радиус основания 10. Найдите площадь сечения цилиндра
плоскостью, проходящей параллельно оси цилиндра на расстоянии 6 от нее.
Решение.
O
10
10
6
A
B
H
Сечение цилиндра плоскостью, проходящей параллельно его оси – прямоугольник.
Расстояние от оси цилиндра до плоскости сечения равно высоте OH треугольника OAB .
OA  OB  10, OH  6
AB  2 AH  2 OA 2  OH 2  16 .
S сеч  16  5  80
6.В прямом круговом цилиндре, осевое сечение которого квадрат со стороной 12, хорда
CD , равная 6 3 , перпендикулярна диаметру AB . Найти площадь сечения цилиндра
плоскостью CDA1 , если AA1 образующая цилиндра.
Решение.
Если осевое сечение квадрат, значит AA1  12 и диаметр окружности основания
цилиндра AB равен 12. R  AO  OC  6 .
D
H
A
O
C
CH  3 3
 
OH  6 2  3 3
Тогда AH  3
2
 36  27  3
A1 H  12 2  32  3 17
1
S CDA1  CD  A1 H  9 51
2
Домашнее задание.
B
1.Радиус основания конуса равен 6, а высота конуса равна 8. В конусе проведено сечение
плоскостью, проходящей через вершину конуса. Площадь сечения равна 25 3 . Найдите
8
угол между плоскостью основания и плоскостью сечения. Ответ: arccos
.
5 3
2. Высота цилиндра равна 3, а радиус основания равен 13. Площадь сечения цилиндра
плоскостью, проходящей параллельно оси цилиндра, равна 72. Найдите расстояние от
плоскости сечения до центра основания цилиндра. Ответ: 5
3. Две параллельные плоскости, находящиеся на расстоянии 8 друг от друга, пересекают
шар. Получившиеся сечения одинаковы, и площадь каждого из них равна 9  . Найдите
площадь поверхности шара. Ответ: 20  .
Самостоятельная работа
1. Дан куб ABCDA1 B1C1 D1 . Через точки A, B1 и точку K ребра CC1 такую, что
CK : KC1  2 :1проведена секущая плоскость. Найдите площадь полной
поверхности куба, если площадь сечения равна 54.
2. В правильной четырехугольной пирамиде SABCD с вершиной S все ребра равны
1. Точка M - середина ребра SC. Найдите площадь сечения этой пирамиды,
3 11
проходящего через точки M , A и D . Ответ:
16
3. В правильной треугольной пирамиде SABC с основанием ABC проведено сечение
через середины ребер AB и BC и вершину S . Найдите площадь этого сечения,
если боковое ребро пирамиды равно 10, а сторона основания равна 12. Ответ:
3 55 .
4. В правильной треугольной призме ABCA1 B1C1 стороны основания равны 6,
боковые ребра равны 4. Изобразите сечение, проходящее через вершины A, B и
9
91
середину ребра A1C1 . Найдите его площадь. Ответ:
4
5. Через середину высоты правильной четырехугольной пирамиды проведено
сечение, перпендикулярное боковому ребру. Найдите площадь этого сечения, если
длина бокового ребра равна 4, а угол между боковыми ребрами, лежащими в одной
грани равен 600. (тренировочный вариант 31)
6. В прямоугольном параллелепипеде ABCDA1 B1C1 D1 AB  BC  10 2 , AA1  2 7 .
Сечение параллелепипеда проходит через точки B и D и образует с плоскостью
7
. Найдите площадь сечения. Ответ: 112
ABC угол   arctg
3
7. В правильной шестиугольной призме ABCDEFA1 B1C1 D1 E1 F1 все ребра равны
2.Найдите площадь сечения, проходящего через вершины A, D и C1 . Ответ: 3 7 .
8. В правильной четырехугольной пирамиде SABCD с основанием ABCD проведено
сечение через середины ребер AB и BC и вершину S . Найдите расстояние от
плоскости этого сечения до середины высоты пирамиды, если все ребра пирамиды
2
равны 8. Ответ: 2 .
3
9. Радиус основания конуса равен 12, а высота конуса равна 5. В конусе проведено
сечение плоскостью, проходящей через вершину конуса и взаимно
перпендикулярные образующие. Найдите расстояние от плоскости сечения до
5 119
центра основания конуса. Ответ:
.
13
10.