Таблица соответствия содержания учебника с привязкой к ГОС и
реклама
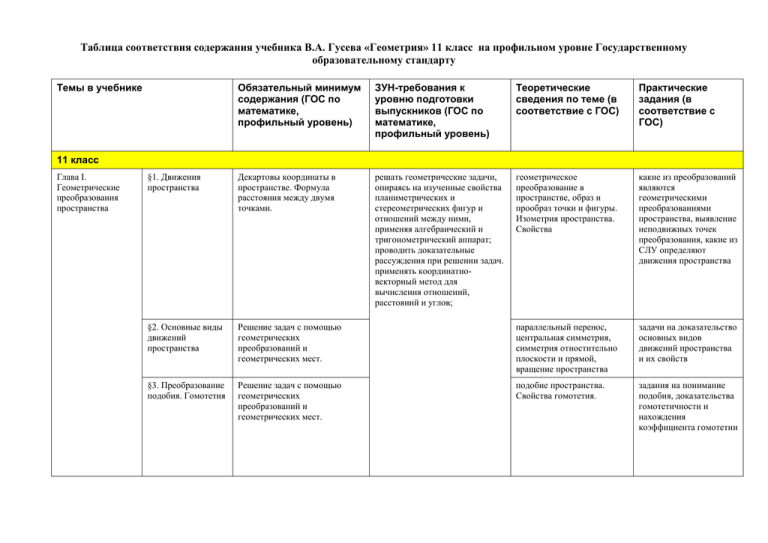
Таблица соответствия содержания учебника В.А. Гусева «Геометрия» 11 класс на профильном уровне Государственному образовательному стандарту Темы в учебнике Обязательный минимум содержания (ГОС по математике, профильный уровень) ЗУН-требования к уровню подготовки выпускников (ГОС по математике, профильный уровень) Теоретические сведения по теме (в соответствие с ГОС) Практические задания (в соответствие с ГОС) §1. Движения пространства Декартовы координаты в пространстве. Формула расстояния между двумя точками. решать геометрические задачи, опираясь на изученные свойства планиметрических и стереометрических фигур и отношений между ними, применяя алгебраический и тригонометрический аппарат; проводить доказательные рассуждения при решении задач. применять координатновекторный метод для вычисления отношений, расстояний и углов; геометрическое преобразование в пространстве, образ и прообраз точки и фигуры. Изометрия пространства. Свойства какие из преобразований являются геометрическими преобразованиями пространства, выявление неподвижных точек преобразования, какие из СЛУ определяют движения пространства §2. Основные виды движений пространства Решение задач с помощью геометрических преобразований и геометрических мест. параллельный перенос, центральная симметрия, симметрия отностительно плоскости и прямой, вращение пространства задачи на доказательство основных видов движений пространства и их свойств §3. Преобразование подобия. Гомотетия Решение задач с помощью геометрических преобразований и геометрических мест. подобие пространства. Свойства гомотетия. задания на понимание подобия, доказательства гомотетичности и нахождения коэффициента гомотетии 11 класс Глава I. Геометрические преобразования пространства Глава II. Многогранники Глава III. Поверхности и тела вращения §4. Общие сведения о многогранниках Вершины, ребра, грани многогранника. Развертка. Многогранные углы. Выпуклые многогранники. Представление о правильных многогранниках (тетраэдр, куб, октаэдр, додекаэдр и икосаэдр). Теорема Эйлера. §5. Изображение многогранников на плоскости и построения на изображениях Изображение пространственных фигур. Сечения многогранников. Построение сечений. Параллельное проектирование. §6. Призмы и пирамиды Призма, ее основания, боковые ребра, высота, боковая поверхность. Прямая и наклонная призма. Правильная призма. Параллелепипед. Куб. Пирамида, ее основание, боковые ребра, высота, боковая поверхность. Треугольная пирамида. Правильная пирамида. Усеченная пирамида. §7. Цилиндрическая поверхность. Цилиндр Цилиндр. Основание, высота, боковая поверхность, образующая, развертка. Осевые сечения и сечения параллельные основанию. Цилиндрические поверхности. Формулы площади поверхности цилиндра понятие и определение многогранника, понятия вершин, ребер и граней, определение выпуклого многогранника, определение призмы, параллелепипеда, пирамиды,, правильные многогранники. Теорема Эйлера. задания на доказательство свойств многогранников и правильных многогранников соотносить трехмерные объекты с их описаниями, чертежами, изображениями; изображать геометрические тела, выполнять чертеж по условию задачи; • строить сечения многогранников демонстрационые примерыизображение пространственных фигур на плоскости, построение сечений задания на построение сечений вычислять углы в пространственных конфигурациях, решать геометрические задачи, опираясь на изученные свойства планиметрических и стереометрических фигур и отношений между ними, применяя алгебраический и тригонометрический аппарат; проводить доказательные рассуждения при решении задач, доказывать основные теоремы курса;строить сечения многогранников и изображать сечения тел вращения основные свойства призмы, параллелипипеда, пирамиды, определение ортогонального сечения призмы, площадь поверхности многогранника, призмы и пирамиды задания на нахождение площади полной и боковой поверхностей прямая круговая цилиндрическая поверхность и прямой круговой цилиндр, площадь поверхности цилиндра задачи с опорой на изученные свойства цилиндра, его сечений. задачи на развертку боковой поверхности цилиндра §8. Коническая поверхность. Конус конус. Усеченный конус. Основание, высота, боковая поверхность, образующая, развертка. Осевые сечения и сечения параллельные основанию, конические поверхности. Эллипс, гипербола, парабола как сечения конуса. Формулы площади поверхности конуса. Формулы площади сферы. прямая круговая коническая поверхность, сечения конической поверхности, §9. Сфера, описанная около многогранника сфера, описанная около многогранника. определение сферы, описанной около многогранника. Необходимое и достаточное условие описания сферы около пирамиды. единственность такой сферы §10. Сфера, вписанная в многогранник Сфера, вписанная в многогранник, определение сферы, вписанной во многогранник. Теорема о единстсвенности вписанной сферы в тетраэдр. Прямой круговой конус. развертка боковой поверхности конуса. Пирамида, вписанная в конус. Площадь боковой поверхности конуса задания по теме Конусплощадь сечения, плоскости и оси симметрии, площадь боковой поверхности Глава IV. Объемы геометрических тел §11. Сфера и шар Шар и сфера, их сечения. Уравнения сферы. Касательная плоскость к сфере. Формулы площади сферы. §12. Объем призмы Понятие об объеме тела. Формулы объема куба, параллелепипеда, призмы. §13. Объем пирамиды Формулы объема пирамиды вычислять объемы и площади поверхностей пространственных тел и их простейших комбинаций. • вычисления длин, площадей и объемов реальных объектов при решении практических задач, используя при необходимости справочники и вычислительные устройства. сфера как поверхность вращения, оси сферической поверхности, взаимное расположение плоскости и сферы, касательная плоскость к сфере, взаимное расположение прямой и сферы, площадь сферической поверхности, шар, уравнение сферы, уравнение плоскости, касательной к сфере задания на нахождение геометрического места касательных к шару, центров сфер, сечения шара, взаимное расположение шара и конуса определение объема геометрического тела, разбиение n-угольной призмы на треугольные, достраивание треугольной призмы до параллелипипеда, объем прямоугольного параллелепипеда, объемы произвольного параллелепипеда и призмы задания на вычисление объема параллелепипеда сведение задачи о нахождении объема nугольной пирамиды к задаче о нахождении объема треугольной пирамиды, объем пирамиды, объем многогранника. Равновеликость и равносоставленность. задания на вычисление объемов многогранников Глава V. О симметрии многогранников §14. Объемы цилиндра, конуса и шара Формулы объема цилиндра, конуса, шара §15. Метод сечений в вычислении объемов тел Отношение объемов подобных тел. §16. О понятии "симметрия" Понятие о симметрии в пространстве (центральная, осевая, зеркальная). понятие "симметрия", плоскостная симметрия и осевые вращения, осевые и центральные симметрии, поворотные симметрии §17. О подсчете симметрий призм и пирамид Симметрии в кубе, в параллелепипеде, в призме и пирамиде. симметрия в треугольной правильной призме, правильном параллелепипеде, четырехугольной пирамиде, виды и число симметрий тетраэдра строить сечения многогранников и изображать сечения тел вращения объем цилиндра, объем конуса, объем тел вращения, объем шара нахождение объемов цилиндра, конуса, усеченного конуса, шара принцип Кавальери, формула Симпсона, примеры использования для вычисления объемов тел задания на доказательство формулы для вычисления объема шарового сегмента