Может ли произойти покрытие Юпитера Луной во время затмения Луны?... Переменная звезда
реклама
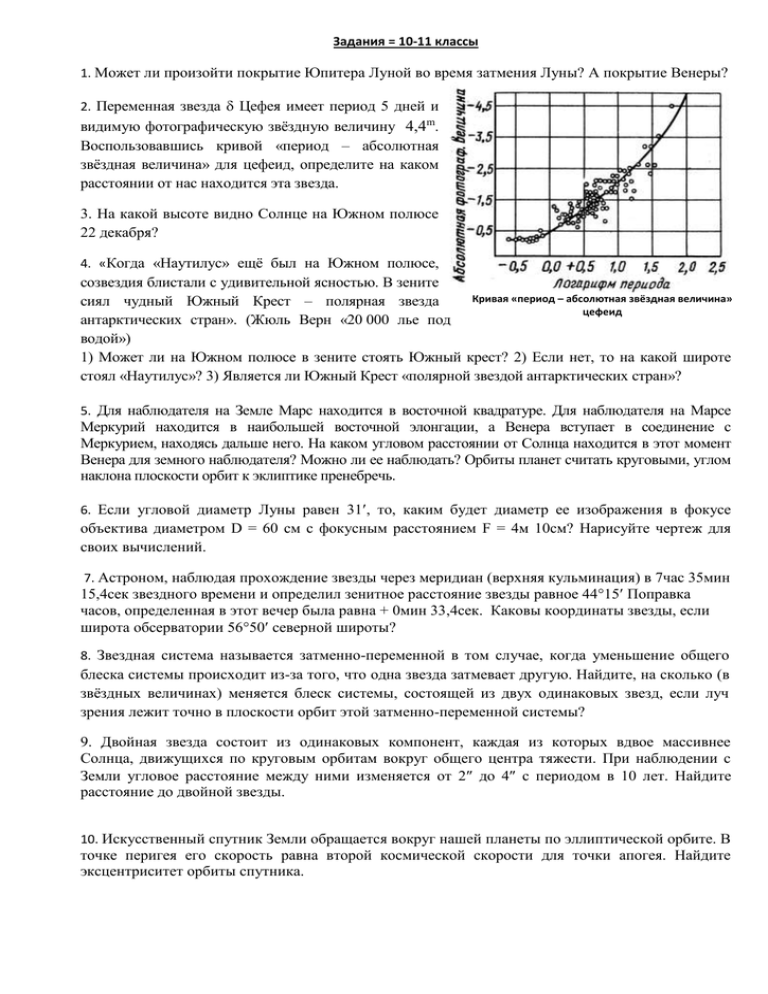
Задания = 10-11 классы 1. Может ли произойти покрытие Юпитера Луной во время затмения Луны? А покрытие Венеры? 2. Переменная звезда Цефея имеет период 5 дней и видимую фотографическую звёздную величину 4,4m. Воспользовавшись кривой «период – абсолютная звёздная величина» для цефеид, определите на каком расстоянии от нас находится эта звезда. 3. На какой высоте видно Солнце на Южном полюсе 22 декабря? 4. «Когда «Наутилус» ещё был на Южном полюсе, созвездия блистали с удивительной ясностью. В зените Кривая «период – абсолютная звёздная величина» сиял чудный Южный Крест – полярная звезда цефеид антарктических стран». (Жюль Верн «20 000 лье под водой») 1) Может ли на Южном полюсе в зените стоять Южный крест? 2) Если нет, то на какой широте стоял «Наутилус»? 3) Является ли Южный Крест «полярной звездой антарктических стран»? 5. Для наблюдателя на Земле Марс находится в восточной квадратуре. Для наблюдателя на Марсе Меркурий находится в наибольшей восточной элонгации, а Венера вступает в соединение с Меркурием, находясь дальше него. На каком угловом расстоянии от Солнца находится в этот момент Венера для земного наблюдателя? Можно ли ее наблюдать? Орбиты планет считать круговыми, углом наклона плоскости орбит к эклиптике пренебречь. 6. Если угловой диаметр Луны равен 31, то, каким будет диаметр ее изображения в фокусе объектива диаметром D = 60 см с фокусным расстоянием F = 4м 10см? Нарисуйте чертеж для своих вычислений. 7. Астроном, наблюдая прохождение звезды через меридиан (верхняя кульминация) в 7час 35мин 15,4сек звездного времени и определил зенитное расстояние звезды равное 4415 Поправка часов, определенная в этот вечер была равна + 0мин 33,4сек. Каковы координаты звезды, если широта обсерватории 5650 северной широты? 8. Звездная система называется затменно-переменной в том случае, когда уменьшение общего блеска системы происходит из-за того, что одна звезда затмевает другую. Найдите, на сколько (в звёздных величинах) меняется блеск системы, состоящей из двух одинаковых звезд, если луч зрения лежит точно в плоскости орбит этой затменно-переменной системы? 9. Двойная звезда состоит из одинаковых компонент, каждая из которых вдвое массивнее Солнца, движущихся по круговым орбитам вокруг общего центра тяжести. При наблюдении с Земли угловое расстояние между ними изменяется от 2 до 4 с периодом в 10 лет. Найдите расстояние до двойной звезды. 10. Искусственный спутник Земли обращается вокруг нашей планеты по эллиптической орбите. В точке перигея его скорость равна второй космической скорости для точки апогея. Найдите эксцентриситет орбиты спутника. Решения = 10-11 классы 1. Во время лунного затмения Луна находится напротив Солнца, поэтому покрытия Луной Венеры, которая отходит от Солнца не дальше 47 произойти не может. Покрытие Юпитера Луной может произойти (если Юпитер в противостоянии). 2. Воспользовавшись кривой, находим, что для цефеиды с периодом 5 суток (lg5=0,699) абсолютная звёздная величина составляет M-1,5m. M=m+5-5lgr. Расстояние (в парсеках): 3. 22 декабря – день зимнего солнцестояния (в южном полушарии в это время лето), склонение Солнца в этот день по модулю равно углу наклона эклиптики к небесному экватору 23,5 (само склонение солнца =-23,5). Поскольку на Южном полюсе небесный экватор совпадает с горизонтом и все светила движутся параллельно горизонту, высота Солнца в этот день составит 23,5. 4. 1) Южный Крест на Южном полюсе не может быть в зените, т.к. склонения звёзд этого созвездия близки к -60. 2) «Наутилус» находился не на южном полюсе Земли, а около 60 южной широты – именно там Южный Крест кульминирует около зенита. 3) Южный Крест не может быть «полярной звездой антарктических стран». Это не звезда, а созвездие, занимающее на небе область с 55 до 64 южного склонения. Южный полюс мира лежит в созвездии Октанта, близ звезды Октанта (пятой величины). Октанта и есть южная полярная звезда. 5. Пусть r1, r2, r3, r4 – радиусы орбит соответственно Меркурия, Венеры, Земли и Марса (их можно взять в справочнике в а.е.), – угол Марс-СолнцеЗемля. Тогда r3 48о.9. r4 arccos Венера Пусть – угол Марс-Солнце-Меркурий. Тогда Ме рк ур ий r arccos 1 75o.3. r4 Пусть – угол Меркурий-Солнце-Венера. Тогда r1 57 o.6. r2 r4 360 o 178o.1. Пусть – угол Венера-Солнце-Земля. Тогда r2 r3 , o sin sin 180 r2 sin tg . r3 r 2 cos r1 arccos Теперь, из теоремы синусов можно определить угол Солнце-Земля-Венера: r2 Марс r3 Земля Отсюда получаем значение , равное 48. Очевидно, что Венера настолько близка к Солнцу, что ее наблюдения невозможны. 6. Диаметр изображения Луны легко вычислить, если правильно нарисовать чертеж, на котором изобразить ход лучей света, распространяющегося от крайних точек лунного диска. Из центра объектива (схематически – линзы) идут (немного отклоняясь от оптической оси) две прямые, угол между которыми 31 (лучи, проходящие через центр линзы, не преломляются). Эти прямые пересекают фокальную плоскость, расположенную на расстоянии 4100 мм в точках, расстояние между которыми и есть диаметр изображения Луны в фокусе объектива. Теперь его легко найти из чертежа: d = F, только нужно выразить в радианах: d = 31 4100 мм / 3438 37 мм. Заметим, что диаметр объектива (60 см) никакой роли не играет: размер изображения от него не зависит. 7. В задаче нужно определить экваториальные координаты звезды и . 1) Определение прямого восхождения . Известно, что звездное время s = + t . В момент верхней кульминации часовой угол t = 0h, следовательно s = . Если показание часов в момент верхней кульминации SТ и поправка часов uТ, то s = ST + uT = , следовательно, прямое восхождение = 7h 35m48,8s. 2) Для определения склонения было измерено зенитное расстояние z = 44 15. z 90 - , следовательно, верхняя кульминация происходит к югу от зенита. h = 90 - + . h = 90 - z, следовательно = - z = 56 20 - 44 15 = 12 05. 8. Световой поток во время затмения изменяется точно в 2 раза. По формуле Погсона Е1Е2 = 2.5m = 2; m 0,4 = lg2. m = lg20,4 0,75m 9. Перейдем для простоты в систему отсчета, связанную с одной из звезд. В этом случае вторая Земля обращается вокруг нее по круговой траектории. Так как расстояние между звездами постоянно, видимое угловое расстояние между ними может изменяться только из-за эффекта проекции, связанного с тем, что мы наблюдаем систему под некоторым углом. Как видно из рисунка, когда угловое расстояние между звездами достигает 4'' максимума (4), прямая, соединяющая их, перпендикулярна направлению на Звезда 2 Звезда 1 Землю. Но это происходит дважды за орбитальный период звезд T, составляющий, таким образом, 20 лет. Если выразить суммарную массу звезд M в массах Солнца (она будет равна 4), то расстояние между звездами, выраженное в астрономических единицах, составляет a (T 2 M )1 3 11.7. Расстояние в 11.7 а.е. видно с Земли под углом 4, следовательно, двойная звезда находится в 2.9 пк от нас. 10. Обозначим большую полуось орбиты спутника через a, а ее эксцентриситет через e. Скорость спутника в точке перигея составляет vP GM 1 e . a 1 e Здесь M – масса Земли. В то же время эта скорость равна второй космической скорости на апогейном расстоянии спутника, равном a(1+e): vP Из данных формул мы получаем уравнение 2GM . a (1 e) 1e 2 , 1e 1e которое можно переписать в виде e 2 4e 1 0. Уравнение имеет два решения: e 2 5. Физический смысл имеет только решение со знаком «+». Эксцентриситет орбиты спутника равен 0.236.