Произвольный треугольник
реклама
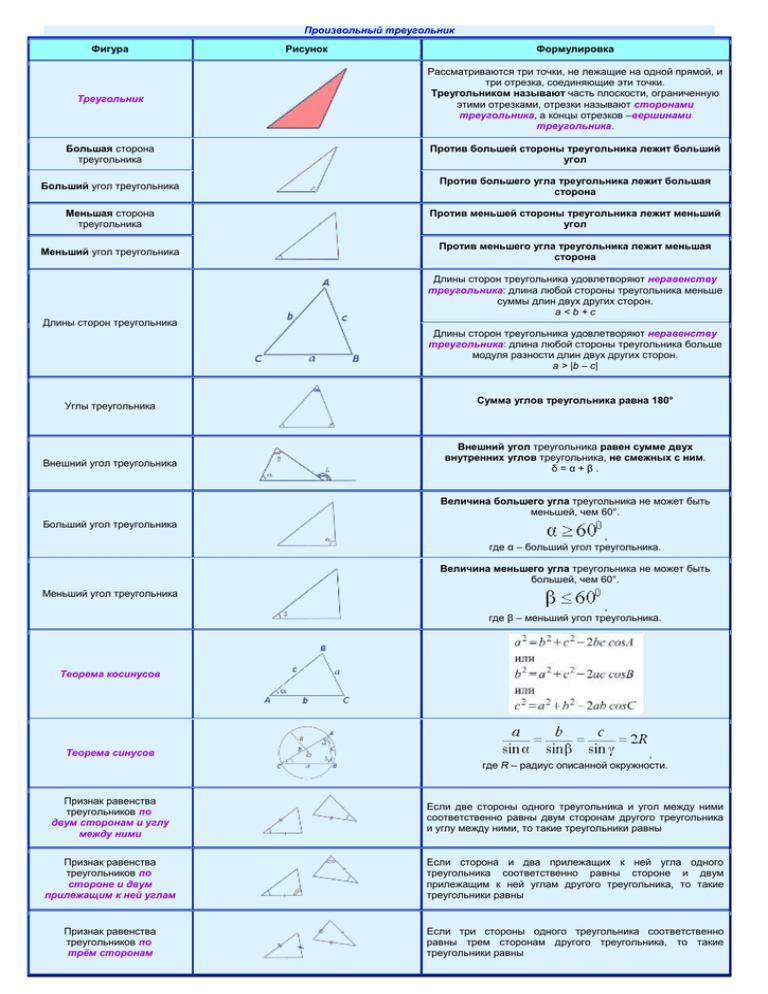
Произвольный треугольник Фигура Рисунок Формулировка Треугольник Рассматриваются три точки, не лежащие на одной прямой, и три отрезка, соединяющие эти точки. Треугольником называют часть плоскости, ограниченную этими отрезками, отрезки называют сторонами треугольника, а концы отрезков –вершинами треугольника. Большая сторона треугольника Против большей стороны треугольника лежит больший угол Больший угол треугольника Против большего угла треугольника лежит большая сторона Меньшая сторона треугольника Против меньшей стороны треугольника лежит меньший угол Меньший угол треугольника Против меньшего угла треугольника лежит меньшая сторона Длины сторон треугольника удовлетворяют неравенству треугольника: длина любой стороны треугольника меньше суммы длин двух других сторон. a<b+c Длины сторон треугольника Длины сторон треугольника удовлетворяют неравенству треугольника: длина любой стороны треугольника больше модуля разности длин двух других сторон. a > |b – c| Углы треугольника Внешний угол треугольника Сумма углов треугольника равна 180° Внешний угол треугольника равен сумме двух внутренних углов треугольника, не смежных с ним. δ=α+β. Величина большего угла треугольника не может быть меньшей, чем 60°. Больший угол треугольника , где α – больший угол треугольника. Величина меньшего угла треугольника не может быть большей, чем 60°. Меньший угол треугольника , где β – меньший угол треугольника. Теорема косинусов Теорема синусов , где R – радиус описанной окружности. Признак равенства треугольников по двум сторонам и углу между ними Если две стороны одного треугольника и угол между ними соответственно равны двум сторонам другого треугольника и углу между ними, то такие треугольники равны Признак равенства треугольников по стороне и двум прилежащим к ней углам Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны Признак равенства треугольников по трём сторонам Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны Признак подобия треугольников по двум сторонам и углу между ними Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника, а углы, заключённые между этими сторонами равны, то такие треугольники подобны Признак подобия треугольников по двум углам Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны. Признак подобия треугольников по трём сторонам Если стороны одного треугольника пропорциональны сторонам другого треугольника, то такие треугольники подобны Медиана Свойства медиан треугольника Медиана треугольника — это отрезок, соединяющий вершину треугольника с серединой противолежащей стороны этого треугольника. 1. Медиана разбивает треугольник на два треугольника одинаковой площади. 2. Медианы треугольника пересекаются в одной точке, которая делит каждую из них в отношении 2:1, считая от вершины. Эта точка называется центром тяжести треугольника. 3. Весь треугольник разделяется своими медианами на шесть равновеликих треугольников. Все три медианы треугольника пересекаются в одной точке. Длина медианы Биссектриса Биссектрисой треугольника называется отрезок биссектрисы угла треугольника, соединяющий вершину с точкой на противолежащей стороне этого треугольника 1. Биссектриса угла — это геометрическое место точек, равноудаленных от сторон этого угла. 2. Биссектриса внутреннего угла треугольника делит противолежащую сторону на отрезки, пропорциональные прилегающим сторонам: Свойства биссектрис треугольника 3. В любом треугольнике все три биссектрисы пересекаются в одной точке. 4. Точка пересечения биссектрис треугольника является центром окружности, вписанной в этот треугольник. Длина биссектрисы треугольника d ac bc , å ab ab Длины биссектрисы CD и высоты CE связаны следующей формулой: Длины биссектрисы и высоты Средняя линия треугольника отрезок, соединяющий середины двух сторон треугольника. Средняя линия треугольника параллельна третьей стороне и равна ее половине. Свойство средней линии треугольника В любой треугольник можно вписать окружность, причем только одну. Центром вписанной в треугольник окружности является точка, в которой пересекаются все Центр и радиус вписанной окружности биссектрисы треугольника. a, b, c – стороны треугольника, S –площадь, r – радиус вписанной окружности, p – полупериметр Центр и радиус описанной окружности 1. Около любого треугольника можно описать окружность. Центром описанной около треугольника окружности является точка, в которой пересекаются все серединные перпендикуляры, проведённые к сторонам треугольника. Центр описанной около тупоугольного треугольника окружности лежит вне треугольника. 2. Для любого треугольника справедливы равенства (теорема синусов): , где a, b, c – стороны треугольника, A, B, С – углы треугольника, R – радиус описанной окружности. 3. Для любого треугольника справедливо равенство: a – любая сторона, ha – высота, опущенная на эту сторону a и b – две любые стороны, С – угол между ними Площадь . a, b, c – стороны, p – полупериметр, формулу называют«Формула Герона» a – любая сторона, B, С – прилежащие к ней углы a, b, c – стороны, r – радиус вписанной окружности, p – полупериметр a, b, c – стороны, R – радиус описанной окружности S = 2R2 sin A sin B sin C A, B, С – углы, R – радиус описанной окружности a – любая сторона, ha – высота, опущенная на эту сторону Отношение площадей подобных треугольников равно квадрату коэффициента подобия Если на сторонах AB и BC треугольника ABC взяты соответственно точки C1 и A1, а точка B1 взята на продолжении стороны AC за точку C, то точки C1, A1 и B1 лежат на одной прямой тогда и только тогда, когда выполнено равенство Теорема Менелая Формула Пика Площадь многоугольника с целочисленными вершинами равна В + Г/2 − 1, где В есть количество целочисленных точек внутри многоугольника, а Г — количество целочисленных точек на границе многоугольника. В = 7, Г = 8, S=В + Г/2 − 1 =10