Условие
реклама
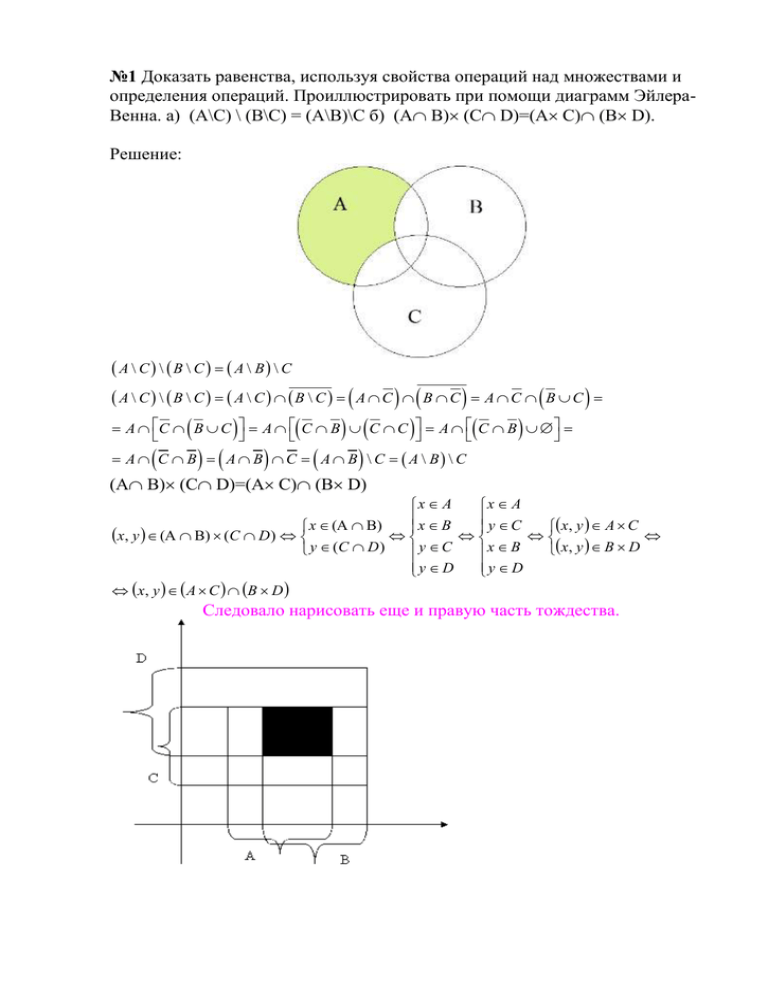
№1 Доказать равенства, используя свойства операций над множествами и
определения операций. Проиллюстрировать при помощи диаграмм ЭйлераВенна. а) (A\C) \ (B\C) = (A\B)\C б) (A B) (C D)=(A C) (B D).
Решение:
A \ C \ B \ C A \ B \ C
A \ C \ B \ C A \ C B \ C A C B C A C B C
A C B A B C A B \ C A \ B \ C
A C B C A C B C C A C B
(A B) (C D)=(A C) (B D)
x A
x A
y C
x (A
x , y A C
x B
x, y (A C D
y C D
x , y B D
y C
x B
y D
y D
x , y A C B D
Следовало нарисовать еще и правую часть тождества.
№2 Даны два конечных множества: А={a,b,c}, B={1,2,3,4}; бинарные
отношения P1 A B, P2 B2. Изобразить P1, P2 графически. Найти
P=(P2◦P1)–1. Выписать области определения и области значений всех трех
отношений: P1, P2, Р. Построить матрицу [P2], проверить с ее помощью,
является
ли
отношение
P2 рефлексивным,
симметричным,
антисимметричным, транзитивным. P1 = {(a,1),(a,2),(a,4),(b,1),(b,4),(c,3)};
P2 = {(1,1),(2,4),(2,1),(3,3),(4,2),(4,1)}.
Решение:
Графическое представление отношения P1 ( P2 ) изображено на рис. 1 (2).
1
2
1
a
2
1
b
4
4
c
3
Рис.1
4
2
3
3
Рис.2
Суперпозицией бинарных отношений R и S называется множество:
R S x, y | z : xSz zRy
. Исходя из этого определения,
P2 P1 a,1, a,4, a,2, b,1, b,2, c,3.
Инверсией бинарного отношения R называется множество:
R1 x, y | y, x R
. Исходя из этого определения,
1
P P2 P1 1, a , 4, a , 2, a , 1, b , 2, b , 3, c .
Областью определения отношения R называется множество:
Dom R x | y : x, y R
. Областью значений отношения R называется
Im R y | x : x, y R
множество:
. Исходя из этого определения,
DomP1 a, b, c ; Im P1 1, 2,3, 4
DomP2 1, 2,3, 4 ; Im P2 1, 2,3, 4
DomP 1, 2,3, 4 ; Im P a, b, c
Матрица
1
1
P2
0
1
P2 бинарного отношения
0 0 0
0 0 1
0 1 0
1 0 0
P2 :
Отношение P2 не рефлексивное, так как на главной диагонали матрицы P2
есть нулевой элемент.
T
P
P
2
2
Отношение будет симметричным, если
, однако:
P2 T
1
0
0
0
1 0 1 1
0 0 1 1
0 1 0 0
1 0 0 1
0 0 0
0 0 1
P2
0 1 0
1 0 0
поэтому отношение P2 не симметричное.
Отношение будет антисимметричным, если поэлементное произведение
T
P2 P2 E , где Е - единичная матрица.
P2 P2 T
1
1
0
1
0 0 0 1
0 0 1 0
0 1 0 0
1 0 0 0
1 0 1 1
0 0 1 0
0 1 0 0
1 0 0 0
0 0 0
0 0 1
0 1 0
1 0 0
Неверно перемножено. Произведение ПОЭЛЕМЕНТНОЕ, логическое.
Условие не выполнено, поэтому отношение P2 не антисимметричное.
Отношение P2 не транзитивное, так как не выполняется соотношение
P2
P2 P2 :
1 0 0
1 0 0
P2 P2
0 0 1
1 1 0
P2 P2 4,4 1 0
0 1
1 1
0 0
0 1
0 0 0 1
0 0 1 1
0 1 0 0
1 0 0 1
0 0 0
1 0 0
0 1 0
0 0 1
Остальное верно.
№5 Бригада из десяти взломщиков одновременно выходит на грабеж трех
разных магазинов. Сколькими способами они могут разделиться, если в
каждой группе должно быть не менее двух человек? Сколькими способами
их после задержания могут рассадить по четырем одинаковым камерам (не
менее чем по одному в каждую)?
1) Распределение 10-ти взломщиков для грабежа 3-х разных магазинов – это
задача размещения 10-ти предметов по 3-м различным ящикам так, что в
каждом ящике будет хотя бы два предмета.
Вообще-то гораздо разумнее решать задачу через разбиения.
Разместить m предметов по n ящикам так, чтобы в каждом ящике было не
менее одного предмета, можно N s m, n способами,
n
s m, n 1
k 1
nk
Cnk k m - число Стирлинга 1-го рода.
Разместить 10 предметов по 3 ящикам так, чтобы в r ящиках было по 1
предмету, а в остальных 3 r ящиках было не менее одного предмета, можно
N r C 3r C10r r! s 10 r ,3 r способами, так как r ящиков из 4-х можно выбрать
C 4r способами и выбрать
r предметов из 10-ти можно C10r способами;
разложить r предметов по r ящикам можно r ! способами.
По формуле включений и исключений получаем, что число распределений,
при котором в каждом ящике оказывается не менее двух предметов, равно
1
N 0 N N 1 N 2 s 10,3 C31C10
1! s 9,2 C32C102 2! s 8,1
s 10,3 1 C31 110 1 C32 210 1 C33 310 3 3 210 310 55980
2
1
0
s 9,2 1 C21 19 1 C22 2 9 2 2 9 510; s8,1 1
1
0
10 взломщиков могут разделится для грабежа 3-х разных магазинов (в
каждой группе не менее двух человек) числом способов
N 0 55980 3 10 510 3 45 2 1 40950 .
2) Распределение 10-ти взломщиков по 4-м одинаковым камерам (не менее
чем по одному в каждую) – это разбиение множества из 10-ти предметов на
4 блока. Число способов такого распределения – это число Стирлинга 2-го
1 n
nk
k
m
рода: S m, n 1 Cn k .
n ! k 1
S 10,4
1 4
1k C4k k 10 1 11 C41 110 12 C42 210 13 C43 310 14 C44 410
4! k 1
24
1
4 6 210 4 310 410 34105
24
Ответы верные, хотя решение сильно не оптимальное.
№10 Взвешенный граф задан матрицей длин дуг. Нарисовать граф. Найти:
а) остовное дерево минимального веса;
б) кратчайшее расстояние от вершины v2 до остальных вершин графа,
используя алгоритм Дейкстры.
Решение:
Нарисуем граф:
а) Найдем остовное дерево минимального веса.
Этап 1:
Этап 2:
Этап 1: включаем в остовное дерево все рёбра с наименьшим весом 1, так как
включение каждого последующего ребра не приводит к образованию цикла.
Этап 2: включаем в остовное дерево все рёбра с весом 2, кроме ребра между
вершинами 2 и 6, так как включение каждого последующего ребра не
приводит к образованию цикла.
Поскольку все вершины соединены, то построение остовного дерева
закончено. вес дерева?



