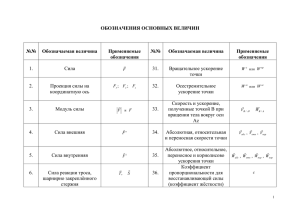
ДИНАМИКА 1. Динамика материальной точки 1.1. Основные
advertisement

ДИНАМИКА 1. Динамика материальной точки 1.1. Основные понятия и определения Предметом динамики является изучение движения материальных тел под действием сил. Понятие о силе было введено в статике. Силы в статике мы считали постоянными. В динамике наряду с постоянными силами рассматриваются силы, изменяющиеся по модулю и направлению. В динамике при изучении движения принимают во внимание инертность тел. Инертность проявляется в том, что тело сохраняет движение в отсутствие действующих на него сил, а когда силы начинают действовать, то скорости точек тела меняются не мгновенно, а постепенно и тем медленнее, чем больше инертность тела. Количественной мерой инертности является масса тела. В общем случае движение тела зависит еще и от распределения масс в теле. В качестве материальных объектов в механике рассматриваются материальная точка, абсолютно твердое тело и система материальных точек или тел. Материальной точкой называется точка, обладающая массой. Абсолютно твердое тело – это материальное тело, в котором расстояния между двумя любыми точками остаются неизменными. Механической системой материальных точек называется такая их совокупность, в которой положение и движение каждой точки зависит от положения и движения всех остальных. 1.2. Законы динамики Галилея-Ньютона В основу динамики положены следующие законы (аксиомы), являющиеся обобщением практической деятельности людей и проверяемые на опыте. 1. Существует инерциальная система отсчета. В такой системе материальная точка находится в покое или движется прямолинейно и равномерно, если на нее не действуют силы. 2. В инерциальной системе отсчета вектор ускорения материальной точки пропорционален вектору силы, действующей на эту точку. Это – основной закон динамики, имеющий фундаментальное значение для всей динамики. 3. Две материальные точки взаимодействуют так, что силы взаимодействия равны по величине, противоположны по направлению и имеют общую линию действия. ~3~ 4. Систему сил, действующих на материальную точку, можно заменить равнодействующей. Ускорение точки под действием системы сил равно ускорению под действием равнодействующей. 1.3. Дифференциальные уравнения движения материальной точки Основной закон динамики можно рассматривать одновременно как дифференциальное уравнение движения точки в векторной форме: dr d 2r m 2 Fr, ,t . dt dt Проектируя это векторное уравнение на те или иные оси координат, можно получить различные формы скалярных дифференциальных уравнений движения материальной точки. Дифференциальные уравнения движения точки в декартовой системе координат: n n n k 1 k 1 k 1 mx Fkx ; my Fky ; mz Fkz , (1.1) где m – масса, x, y, z – координаты точки; Fkx , Fky , Fkz – проекции k-ой силы на оси координат. Дифференциальные уравнения движения точки в естественной системе координат: n n n V2 dVτ (1.2) Fkn ; 0 Fkв , m Fkτ ; m ρ k 1 dt k 1 k 1 где m – масса; – радиус кривизны; Fk , Fkn , Fkв – проекции силы на касательную, главную нормаль, бинормаль в данной точке траектории. Пример. Груз вследствие толчка приобрел начальную скорость V0 и поднимается по шероховатой наклонной плоскости, составляющей угол α с горизонтом; коэффициент трения равен f. Составить дифференциальные уравнения движения груза, если его движение происходит в вертикальной плоскости. Изображаем груз в промежуточном положении на наклонной плоскости. Активной силой будет сила тяжести mg . Реакцию шероховатой наклонной плоскости представляем в виде силы нормального давления N и ~4~ силы трения скольжения Fтр , равной по величине f N и направленной в сторону, противоположную движению. Так как груз движется поступательно, принимаем модель материальной точки. Траектория и силы лежат в одной плоскости, поэтому выбираем плоскую прямоугольную систему координат. Ее начало O совмещаем с начальным положением груза, а ось Ox направляем по наклонной плоскости вправо – вверх. При этом координата груза в промежуточном положении положительна. Находим проекции сил на оси: Fx mg sin α Fтр ; Fy N mg cosα . Дифференциальные уравнения движения груза: mx mg sin α Fтр ; my N mg cosα . Движение груза происходит только вдоль оси x, поэтому y 0 . Следовательно, N mg cosα , что позволяет определить силу трения Fтр mg f cosα . Подставляя значение силы трения в первое уравнение движения груза, получаем дифференциальное уравнение движения груза, поднимающегося по шероховатой наклонной плоскости вследствие толчка: x sin α f cosα g . 1.4. Дифференциальные уравнения относительного движения материальной точки Основной закон динамики и полученные из него дифференциальные уравнения движения материальной точки верны в инерциальной системе отсчета. Во многих случаях задачи динамики целесообразно рассматривать в той или иной неинерциальной системе. Здесь мы получим метод составления уравнений движения материальной точки в неинерциальной системе отсчета. Основной закон динамики ma F содержит абсолютное ускорение. Согласно кинематической формуле, a ar ae aс , где ar – относительное ускорение, ae – переносное ускорение, aс – кориолисово ускорение. Подставив в основной закон динамики значение a и перенеся часть членов в правую часть, получим mar F mae maс . ~5~ Введем обозначения Feи mae , Fси maс . Эти величины имеют размерность силы. Будем называть эти векторы соответственно переносной и кориолисовой силой инерции. Тогда уравнение примет вид mar F Feи Fси . (1.3) Получаем правило: Для того чтобы составить дифференциальное уравнение движения материальной точки в неинерциальной системе координат в форме второго закона Ньютона, необходимо к действующим на точку активным силам и реакциям связей присоединить переносную и кориолисову силы инерции. Пусть в подвижной системе координат материальная точка имеет координаты x, y, z . Тогда проекции ее относительного ускорения на эти оси arx x, ary y, arz z . Проектируя векторное уравнение на оси подвижной системы координат, получаем дифференциальные уравнения относительного движения точки: mx Fx Fexи Fсxи , m y Fy Feyи Fсyи , (1.4) mz Fz Fezи Fсzи . Пример. Проволочная полуокружность радиуса R вращается вокруг вертикальной оси с постоянной угловой скоростью . По ней из точки A скользит без трения кольцо M массы m . Найти скорость V1 кольца относительно проволоки в точке B , если его начальная относительная скорость V0 0 . Решение. Свяжем с полуокружностью систему координат (рис. 2). Выбранная подвижная система координат является неинерциальной. Прибавим к действующим на кольцо силе тяжести mg и нормальной реакции N силы инерции: переносную Feи и кориолисову Fси . Так как const , то ae aen R cosφ 2 и Feи mR2 cosφ . ~6~ Сила Feи направлена от оси вращения. Кориолисово ускорение aс 2 Vr и кориолисова сила инерции перпендикулярны плоскости полуокружности. Уравнение движения кольца в векторном виде в форме второго закона Ньютона mar mg N Feи Fси . (a) Найдем проекцию уравнения ( a ) на направление τ , учитывая, что N τ , Fси τ , arτ Rφ : mRφ mg cosφ mR2 cosφsin φ . После деления на mR , замены независимой переменной dφ dφ dφ dφ φ φ dt dφ dt dφ и разделения переменных получим g φ dφ cosφ dφ 2 sin φcosφdφ . R Проинтегрируем это уравнение с учетом заданных начальных условий φ1 600 600 g φ d φ cosφdφ 2 sin φcosφdφ . 0 R 0 0 Здесь φ1 – значение производной φ в точке B . Получим 2 0 φ12 g 0 2 sin 60 sin 60 , 2 R 2 откуда φ1 g 3 3 2 и относительная скорость кольца в точке B R 4 g 3 3 2 . R 4 Видно, что не при всяких значениях параметров задача имеет решение. Чтобы кольцо достигло точки B , должно выполняться условие: 4g . 2 R 3 V1 Rφ1 R ~7~ 1.5. Прямые и обратные задачи динамики Все задачи динамики делятся на прямые и обратные. Прямая задача: зная массу точки и ее уравнения движения, определить равнодействующую приложенных к точке сил. Пусть движение свободной точки массы m задано в координатной форме: x x(t ), y y(t ), z z (t ) . Дважды дифференцируя эти функции по времени и используя уравнения (1.1), находим: Fkx m x, Fky my, Fkz mz . Равнодействующая вычисляется по формуле F F F F 2 2 kx ky kz 2 . Пример. Определить силу, действующую на точку массы m=5 кг, закон движения которой задан уравнениями: x 5t 2 , y 3t (x, y – в метрах, t – в секундах). Fx mx 50 H , Fy my 0, Fz 0, Решение. Найдем т.е. F 50 H . Обратная задача: зная приложенные к свободной материальной точке силы, массу точки, начальные условия (т.е. начальное положение и начальную скорость), определить закон движения. Эта задача называется основной задачей динамики. Чтобы найти уравнения движения точки, необходимо проинтегрировать систему трех обыкновенных дифференциальных уравнений второго порядка. В результате интегрирования этой системы в решении появляются шесть произвольных постоянных. Они определяются по начальным условиям движения. В случае несвободной материальной точки необходимо знать дополнительно уравнения связи, а в роли неизвестных выступают закон движения и реакция связи. Пример. Материальная точка массой m движется из начала координат вдоль оси x с начальной скоростью V0 , испытывая сопротивление движению F , где F b x , b – заданная постоянная. Необходимо определить закон движения точки. Решение. Дифференциальное уравнение движения точки вдоль оси Ox m x Fkx в данном случае приобретает вид: m x b x , или ~8~ b b x 0 . Характеристическое уравнение k 2 k 0 , его корни: m m b k1 0, k2 . Общее решение дифференциального уравнения m x b t m (а) x c1 c2e . Продифференцируем формулу (а) по времени: b mb t (б) x c2 e . m При t 0 уравнения (а) и (б), с учетом начальных условий, принимают вид: b 0 c1 c2 , V0 c2 . (в) m m m Из уравнений (в) находим: c1 V0 , c2 V0 . b b b t m Закон движения x V0 1 e m . b Контрольные вопросы 1. Что является количественной мерой инертности тела? 2. Напишите дифференциальные уравнения движения материальной точки в проекциях на оси неподвижной декартовой системы координат и на естественные оси. 3. Запишите основной закон динамики для относительного движения точки. 4. Чему равны переносная и кориолисова силы инерции материальной точки? 5. Какая система отсчета называется инерциальной? 6. Назовите две основные задачи динамики свободной материальной точки. 7. Как определяются произвольные постоянные интегрирования при решении дифференциальных уравнений движения материальной точки? 8. Сформулируйте обратную задачу динамики материальной точки. ~9~ Таблица 1 Тестовые задания № 1 2 Задание/ответ Схема Материальная точка движется под действием силы F 6τ +8n (Н) с ускорением 5 м/с2 . Масса точки m ... кг . Ответ: 2. Материальная точка движется под действием силы по окружности согласно уравнению S 9t (метры). Модуль силы F ... H . Ответ: 72 Свободная материальная точка массой m 2 кг движется под дейст- 3 вием силы F (5 i 2 j 7 k ) H . Ускорение a ... м/с2 . Тело массой m 2 кг движется по за32 2 πt (метры) под дей sin π 4 ствием силы F . В момент t1 1с модуль силы F (t1 ) ... H . Ответ: 4 кону x 4 5 Материальная точка массой m 3 кг движется под действием системы сил, где F 6 H , с ускорением a ... м/с2 . Ответ: 2 ~ 10 ~ Ответ: 3 2. Введение в динамику механической системы 2.1. Силы внешние и внутренние. Масса системы. Центр масс Действующие на механическую систему активные силы и реакции связей разделяют на внешние силы Fke и внутренние силы Fki . Внешними называют силы, действующие на точки системы со стороны точек, не входящих в систему. Внутренними называют силы, с которыми точки системы действуют друг на друга. Свойства внутренних сил: 1. Геометрическая сумма (главный вектор) внутренних сил системы равняется нулю. 2. Сумма моментов (главный момент) внутренних сил относительно любого центра или оси равняется нулю. Массой механической системы называется сумма масс всех ее материальных точек или тел: n m mk . k 1 Центром масс механической системы называется точка, координаты которой определяются формулами: 1 n 1 n 1 n m x ; y m y ; z mk zk , k k c m k k c m k 1 m k 1 k 1 где xk , yk , zk координаты материальной точки, масса которой mk . xc 2.2. Момент инерции относительно оси. Радиус инерции Момент инерции относительно оси z (или осевой момент инерции) n J z mk hk2 , k 1 где mk масса k - той точки; hk расстояние от этой точки до оси z . Осевой момент инерции является мерой инертности тела при вращательном движении. Моменты инерции относительно осей координат Oxyz J x mk ( yk2 zk2 ) ; J y mk ( zk2 xk2 ) ; J z mk ( xk2 yk2 ) , ~ 11 ~ где ( yk2 zk2 ) , ( zk2 xk2 ) , ( xk2 yk2 ) – квадраты расстояний k-той точки системы до осей Ox, Oy, Oz , соответственно. Радиус инерции механической системы относительно оси z где m масса системы. ρz J z m , 2.3. Моменты инерции относительно параллельных осей Теорема Гюйгенса– Штейнера: момент инерции тела относительно данной оси равен моменту инерции относительно оси, ей параллельной, проходящей через центр масс тела, сложенному с произведением массы тела на квадрат расстояния между осями. 2.4. Моменты инерции некоторых однородных тел Момент инерции однородного тонкого стержня массы М и длины l относительно оси z, проходящей перпендикулярно стержню через его конец (рис. 5, а), равен J Oz ml 2 3 и относительно оси, проходящей через его центр тяжести (рис. 5, б), равен J Cz ml 2 . 12 Момент инерции тонкого однородного кольца с массой m и радиусом R относительно оси z , перпендикулярной плоскости кольца и проходящей через его центр тяжести (рис. 6), равен J Cz mR 2 . Момент инерции однородного круглого цилиндра с массой m и радиусом R (рис. 7) относительно продольной оси z равен mR 2 J Cz . 2 ~ 12 ~ 2.5. Центробежные моменты инерции Проведем через некоторую точку O тела координатные оси Oxyz . Центробежными моментами инерции по отношению к этим осям называют величины n n n k 1 k 1 k 1 J xy mk xk yk ; J xz mk xk zk ; J yz mk yk zk , где xk , yk , zk координаты k – той точки системы с массой mk . Центробежные моменты инерции могут быть положительными, отрицательными и равными нулю. Ось Ox называется главной осью инерции для данной точки механической системы, если центробежные моменты инерции J xz , J xy , содержащие в своих индексах наименование этой оси, равны нулю: J xy 0; J xz 0 . Ось материальной симметрии механической системы является главной осью инерции в любой точке этой оси. Любая прямая, перпендикулярная к плоскости материальной симметрии, является главной осью инерции для точки пересечения прямой с плоскостью. Главные оси инерции, проходящие через центр масс тела, называют главными центральными осями инерции тела. Контрольные вопросы 1. Перечислите свойства внутренних сил механической системы. 2. Чему равна масса системы материальных точек? 3. Как определяется положение центра масс механической системы? 4. Какими величинами характеризуется распределение масс в механической системе? 5. Какие оси называются главными центральными осями инерции? 6. Как связаны моменты инерции относительно двух параллельных осей, одна из которых проходит через центр масс тела? ~ 13 ~ Таблица 2 Тестовые задания № Задание/ответ 1 Однородный цилиндр массой m 2 кг , радиусом R 7 см имеет осевой момент инерции 2 J z ... кг см . Ответ: 49 2 3 4 5 Схема Масса однородного цилиндра m 0,5 кг , радиус R 10 см . Момент инерции J z ... кг см2 . Ответ: 50 Момент инерции шкива J z 27 кг см2 , масса m 3 кг . Радиус инерции ρ z ... м . Ответ: 3 Радиус инерции конуса ρ z 4 м , масса m 3 кг . Момент инерции J z ... кг см2 . Ответ: 48 Момент инерции системы, состоящей из однородных стержня массой m 1кг и кольца массой m 2 кг , относительно оси Oz J Oz ... кг см2 . Ответ: 192 ~ 14 ~ 3. Принцип Даламбера (метод кинетостатики) 3.1. Принцип Даламбера для точки и механической системы Принцип Даламбера устанавливает единый подход к исследованию движения несвободной материальной точки и несвободной материальной системы вне зависимости от вида связей, налагаемых на их движение. Этот подход заключается в придании динамическим уравнениям вида уравнений равновесия, что позволяет при решении задач динамики применять простые и наглядные приемы и методы статики. Если к несвободной материальной точке применить аксиому освобождаемости от связей, то основное уравнение динамики примет вид ma F R . Здесь m масса точки; a ускорение точки; F равнодействующая активных сил; R равнодействующая реакций связей. Введем в рассмотрение вектор силы инерции материальной точки F и ma , получим F R Fи 0. Это уравнение выражает принцип Даламбера для материальной точки: если в любой момент времени к действующим на точку активным силам и реакциям связей присоединить силу инерции, то полученная система сил будет уравновешенной. принцип Даламбера для системы материальных точек: если к активным силам и реакциям связей, действующим на каждую материальную точку системы, добавить силы инерции точек, то в любое мгновение времени полученная система сил будет уравновешенной. 3.2. Следствия из принципа Даламбера для механической системы При движении механической системы геометрическая сумма главных векторов внешних активных сил, реакций внешних связей и сил инерции системы, а также геометрическая сумма главных моментов указанных сил относительно произвольного центра равны нулю в любое мгновение времени F е F и 0 ; M 0е M 0и 0 , ~ 15 ~ F e , M 0e – главный вектор и главный момент внешних сил, включая ре- акции внешних связей, F и , M 0и – главный вектор и главный момент сил инерции. Двум векторным уравнениям соответствуют шесть уравнений в проекциях на оси декартовых координат: Fxe Fxи 0, Fye Fyи 0, Fze Fzи 0, M xe M xи 0, M ye M yи 0, M ze M zи 0 За оси координат можно выбрать любую систему декартовых осей, как неподвижных, так и перемещающихся произвольным образом в пространстве. 3.3. Главный вектор и главный момент сил инерции Главный вектор сил инерции механической системы (в частности, твердого тела) равен произведению массы системы (тела) на ускорение центра масс и направлен противоположно этому ускорению. 1. При поступательном движении тела силы инерции приводятся к равнодействующей F и maC , проходящей через центр масс тела. Здесь m масса тела; aC ускорение центра масс. 2. Вращательное движение. Пусть тело имеет плоскость материальной симметрии xy и вращается вокруг оси Oz , перпендикулярной этой плоскости. Силы инерции такого вращающегося тела приводятся к силе F и maC , приложенной в точке O , и к паре с моментом и M Oz J Oz ε , лежащей в плоскости симметрии тела. При вращательном движении тела вокруг главной центральной оси инерции Сz силы инерции приводятся к одной только паре с и J Cz ε z , лежащей в плоскомоментом M Cz сти симметрии тела. ~ 16 ~ Здесь ε z – проекция углового ускорения и главный момент сил на ось z , M Cz инерции. Силы инерции при плоском движении тела в плоскости материальной симметрии XOY M Cи J C ε ; F и m aС ; F и maС . Пример. Груз 2 массой m2 4m подвешен на нити к барабану 1 радиусом R и массой m1 2m . Момент трения нити о барабан M тр 0,1mgR . ρ 0,707R . Необходимо определить величину углового ускорения ε барабана 1. Решение. По модулю определяем F m2 a , M J1 . Ускорение груза 2 и и определим как a εR . Момент инерции барабана J1 m1 ρ . 2 M O ( FK ) 0 . M и M тр F и R G1 R 0; mR 2 ε 0.1mgR 4mR 2 ε 2mgR 0. Преобразуя полученное выражение, находим: ε 0,38 ~ 17 ~ g . R 3.4. Дифференциальные уравнения движения твёрдого тела Следствия из принципа Даламбера для механической системы позволяют получить дифференциальные уравнения поступательного, вращательного и плоского движения твердого тела. Дифференциальные уравнения поступательного движения тела: mxC Fxe ; myC Fye ; mzC Fze , где Fxe , Fye , Fze – проекции главного вектора внешних сил на оси координат. Дифференциальное уравнение вращательного движения тела n J z φ mz ( Fke ) M zе , k 1 где J z момент инерции тела относительно оси вращения; φ угол поворота тела; M zе главный момент внешних сил относительно оси вращения. Дифференциальные уравнения плоского движения тела: n n n mxC F ; myC F ; J Cz φ mCz ( Fke ) , k 1 e kx k 1 e ky k 1 где xC, yC – координаты центра масс; φ угол поворота тела; J Cz момент инерции относительно оси, перпендикулярной плоскости движения и проходящей через центр масс; Fkxe , Fkye – проекции внешних сил Fke на оси координат. Пример. Вал маховика массой m с радиусом инерции ρ вращается в опорах, обладающих постоянным моментом трения M . Составить дифференциальное уравнение вращения маховика. Решение. Расчетная схема задачи представлена на рисунке 12. Момент инерции маховика J z m ρ2 . Сумма мо- ментов внешних сил относительно оси z M ze M . Подставляем эти величины в дифференциальное уравнение вращательного движения тела, получаем: m ρ 2φ M . ~ 18 ~ Контрольные вопросы 1. Чему равна сила инерции материальной точки? 2. Как направлена сила инерции материальной точки? 3. Чему равна и как направлена сила инерции материальной точки, равномерно движущейся по окружности? 4. Учитываются ли внутренние силы механической системы в принципе Даламбера для механической системы? 5. Как вычислить главный вектор сил инерции механической системы и твердого тела? 6. Твердое тело вращается вокруг неподвижной оси симметрии. Чему равен главный момент сил инерции? 7. Сформулируйте и запишите следствия из принципа Даламбера для механической системы. 8. Запишите дифференциальное уравнение вращательного движения твердого тела. 9. Запишите дифференциальные уравнения плоского движения твердого тела. Таблица 3 Тестовые задания № Задание/ответ Масса груза m 5 кг , угловое ус- 1 2 корение ε 3 рад/с2 , угловая скорость ω 2 рад/с . Модуль главного вектора сил инерции груза F и ... H . Ответ: 30 Силы инерции F1и 4H , F2и 3H . Величина главного вектора сил инерции системы F и ... H . Ответ: 5 ~ 19 ~ Схема Масса однородного диска m 2 кг , 3 угловое ускорение ε 3 рад/с2 . Модуль главного момента сил инерции диска M Ои ... H м . Ответ: 225 Момент инерции 2 1 J A 2кг м , g 10м/c2 , 4 тела M вр 10Н м . Угловое ускорение ε ... рад/с2 . Ответ: 5 5 Однородный диск катится без скольжения под действием силы F 46 Н и силы тяжести; m1 0 , g 10м/c2 . Угловое ускорение ε 6 рад/с2 . Масса диска m ... кг . Ответ: 2 6 7 Приведено два из трёх уравнений плоского движения (в плоскости хОу) твёрдого тела: mxC Fxe ; J Cz φ M Cz F e . Недостающее уравнение … Ответ: myC Fye Приведено два из трёх уравнений поступательного движеe e ния твёрдого тела в пространстве: mxС Fkx , myС Fky . k Недостающее уравнение … ~ 20 ~ k Ответ: mzC Fkze Индивидуальное задание №1 Исследование поступательного и вращательного движений твердого тела Механическая система состоит из колес 1 и 2 и груза 3. К колесу 1 приложена пара сил с моментом M M t или сила P P t . Время t отсчитывается от момента t0 0 , когда угловая скорость колеса 1 равна ω10 ; момент сил сопротивления ведомого колеса 2 равен M С . Массы колес равны m1 и m2 ; для всех вариантов масса груза m3 400 кг . Радиусы больших и малых окружностей колес R1, r1, R2 , r2 . Для всех вариантов r1 0,6R1 , r2 0,7 R2 . Схемы механических систем представлены в таблице 4, а необходимые для решения данные приведены в таблице 5. Требуется найти уравнение движения тела, указанного в последней графе таблицы 5. Определить также натяжение нитей в заданный момент времени, а в вариантах, где имеется соприкасание колес, найти окружное усилие в точке их касания. Колеса, для которых радиусы инерции ρ1 и ρ 2 в таблице 5 не заданы, считать сплошными однородными дисками. Пример выполнения задания. Дано: Механическая система, состоящая из колес 1 и 2 и груза 3 (рис. 13). m1 100 кг; m2 150 кг; m3 400 кг; M 4200 200t H м; М С 2000 Н м; R1 60 см; R2 40 см; r2 20 см; ρ1 20 2 см; ρ2 30 см; ω10 2 рад с. Найти уравнение φ2 f t вращательного движения колеса 2, а также окружное усилие в точке касания колес и натяжение нити в момент времени t1 1 c . Решение. Разделим механизм на отдельные звенья (см. рис. 14). К колесу 1 приложены сила тяжести G1 , момент M , составляющие реакции опоры YA , Z A , окружное усилие S1 и нормальная реакция N1 колеса 2 (см. рис. 14, а). ~ 21 ~ К звену 2 приложены сила тяжести G2 , момент сил сопротивления M C , составляющие реакции опоры YB , Z B , натяжение T нити, к которой подвешен груз, окружное усилие S 2 и нормальная реакция N 2 колеса 1 (рис. 14, б). К грузу 3 приложены сила тяжести G3 и натяжение нити T (рис. 14, в). Согласно закону равенства действия и противодействия: S2 S1 , N2 N1 , T T . Составим дифференциальное уравнение вращения колеса 1 вокруг оси x1 : J1φ1 M kxe 1 , M kxe 1 M S1R1 . Дифференциальное уравнение вращения колеса 1 имеет вид: J1φ1 M S1R1 . (1) Составим дифференциальное уравнение вращения звена 2 вокруг оси x2 . При этом учтем следующее. Для колеса 1 за положительное направление отсчета угла φ1 и моментов сил принято направление против хода часовой стрелки. При вращении колеса 1 в положительном направлении звено 2 вращается по часовой стрелке. Это направление для звена 2 будем считать положительным. J 2φ2 M kxe 2 , M kxe 2 S2 R2 T r2 M C . Дифференциальное уравнение вращения колеса 2 имеет вид: (2) J 2φ2 S2 R2 Tr2 M C . Составим дифференциальное уравнение движения груза (положительное направление движения – вверх): m3 z Fkze , Fkze T G3 . ~ 22 ~ Дифференциальное уравнение поступательного движения груза (3) m3 z T G3 . Составлено три уравнения (1), (2), (3), которые содержат пять неизвестных: силы T и S , угловые ускорения φ1 ,φ2 и линейное ускорение z . Недостающие уравнения получим, составив уравнения связей φ1 / φ2 R2 / R1 , (4) z φ2 r2 . (5) Используем уравнения (3), (4), (5) для того, чтобы исключить из уравнений (1) и (2) неизвестные φ1, z, T . Получим J1φ2 R2 / R1 M S2 R1 , J 2 m3r22 φ2 S2 R2 G3r2 M C . Исключим из этих уравнений неизвестную S 2 и из полученного уравнения найдем M R2 R1 m3 gr2 M C R12 . (6) φ2 J1R22 J 2 m3r22 R12 Моменты инерции J1 m1ρ12, J 2 m2ρ22 . Учитывая исходные данные, находим J1 8 кг м2 ; J 2 13,5 кг м2 . Теперь по формуле (6) получаем φ2 4,034t 0,4597 . (7) Интегрируем это уравнение дважды, используя начальные условия задачи: при t 0 φ20 0, φ20 ω10 R1 R2 , или φ20 3 рад с . Первый интеграл φ2 dφ φ20 2 t t 0 0 4,034 tdt 0,4597 dt ; φ2 2,017t 2 0,4597t 3 . Второй интеграл φ2 dφ φ20 t t t 0 0 2,017 t dt 0,4597 tdt 3 dt ; φ2 0,672 t 3 0,230 t 2 3t . 2 2 0 Мы получили уравнение вращательного движения звена 2. Окружное усилие определяем из уравнения (2): S2 J 2φ2 Tr2 M C / R2 . При t 1c , учитывая (7) и исходные данные, имеем S2 7295 H . Натяжение нити найдем из уравнения (3): T m3 z G3 , или T m3φ2 m3 g . При t 1c T 4285 H . ~ 23 ~ Таблица 4 Схемы механических систем к заданиям №1 задание №1 задание №2 задание №3 задание №4 задание №5 задание №6 ~ 24 ~ продолжение табл. 4 задание №7 задание №8 задание №9 задание №10 задание №11 задание №12 ~ 25 ~ продолжение табл. 4 задание №13 задание №14 задание №15 задание №16 задание №17 задание №18 ~ 26 ~ продолжение табл. 4 задание №19 задание №20 задание №21 задание №22 задание №23 задание №24 ~ 27 ~ задание №25 окончание табл. 4 задание №26 задание №27 задание №28 задание №29 задание №30 ~ 28 ~ Таблица 5 m1 1 100 300 20 60 – 50 2100+20t 1000 2 2 1 2 300 80 70 20 60 – 9800+100t 600 1 0,5 2 3 200 100 60 30 – 25 6100+20t 800 0,5 2,5 1 4 100 250 20 50 – 40 1000+40t 1400 1,5 2 1 5 150 300 30 50 – 30 5500+200t 1500 2 1 3 6 400 250 70 30 – 25 4800+10t 800 3 4 1 7 300 200 60 30 50 20 3000+100t 500 0 3 3 8 300 250 50 40 40 30 9700+50t 500 1 2 1 9 200 100 80 20 65 – 5900+30t 600 2 3 2 10 250 100 40 30 30 – 2500+50t 1200 0 1,5 2 11 150 300 40 60 30 40 3900+50t 1000 1 2 1 12 100 200 30 60 25 – 5700+50t 1500 2 2 1 13 180 100 50 30 40 20 2700+200t 400 0,5 1 2 14 150 80 40 30 30 – 1800+20t 700 1,5 2,5 3 15 300 180 20 50 15 – 700+40t 300 0 1,5 1 16 300 250 60 50 50 40 7300+100t 1200 1 2 1 17 250 100 50 20 40 – 5400+50t 900 2 2 1 18 200 100 20 50 – – 1900+20t 1500 0,5 1 2 19 250 150 50 30 40 25 9900+200t 500 0,5 2 1 20 400 100 50 30 40 – 3700+50t 1200 2 1 2 21 200 150 50 30 45 20 3800+100t 800 1 1,5 2 22 250 100 60 10 50 – 9700+200t 700 2 0,5 1 23 200 80 40 30 30 – 2300+20t 900 0,5 1 2 24 100 200 30 40 – 30 9900+100t 500 1,5 1 1 25 150 80 60 20 – – 4900+40t 800 0 1,5 2 26 250 200 50 40 40 30 3500+150t 600 2 2 1 27 250 150 50 40 45 30 9900+100t 700 1,5 1 1 28 60 200 20 60 – 30 900+10t 1500 0 2 2 29 50 200 20 40 – 35 2100+20t 1000 2 0,5 1 30 300 60 50 20 40 – 7200+50t 700 1,5 1 2 кг m2 кг R1 R2 ρ1 ρ2 M,P MС см см см см Нм, Н Нм ~ 29 ~ ω10 , рад/с t1 , с Тело Вариант Данные для индивидуального задания №1 Индивидуальное задание №2 Применение принципа Даламбера к определению реакций связей Определить реакции внешних связей механической системы: а) в произвольный момент времени – для вариантов 4, 5, 10, 12 – 14, 16 – 18, 21 – 30 (таблица 6); б) в момент времени t t1 – для вариантов 1, 8, 9, 11, 20; в) в тот момент времени, когда угол поворота φ φ1 – для вариантов 2, 3, 6, 7; г) в положении, показанном на чертеже для вариантов 15 и 19. На схемах (таблица 6) плоскость хОу (хАу) горизонтальна, плоскость уОz (yAz) вертикальна. Необходимые для решения данные приведены в таблице 7. Приняты обозначения: ω угловая скорость, ρ радиус инерции. В вариантах 4, 5, 9, 10 – 14, 18, 23, 24, 29, 30 оси координат вращаются вместе с конструкцией. В вариантах 1 – 5, 10 – 15, 18, 19, 23, 24, 29, 30 стержни однородные. В вариантах 6 – 9, 16, 20, 22, 28 диски однородные. В варианте 10 тело 2 рассматривать как материальную точку. В вариантах 17, 21 момент М, действующий на барабан 2, создается электродвигателем, установленным на балке АВ. Пример выполнения задания. Дано: Схема механической системы и размеры (в см) на рис. 15. m1 3кг, m 2 2кг, m3 5кг, l1 30см, l 2 20см, α 30 , ω 120рад/ с const. Найти реакции подпятника A, подшипника B и невесомого стержня DN. Решение. Для определения реакций связей воспользуемся принципом Даламбера. Так как ω=const , действуют только центробежные силы инерции. Главный вектор сил инерции тела определяется по формуле: F ин ma C . Здесь m – масса тела, a C ускорение центра масс тела. Для стержней 1 и 2: ~ 30 ~ F1ин m1 aC1 m1 ω2 0,5l1 sin α; F2ин m2 aC2 m2 ω2 l1 sin α+0,5l2 . Расстояние h от точки О до линии действия силы F1ин : 2 2 h l1 cosα 30 cos30 10 3 (см). 3 3 Составляющие реакций подпятника X A , YA , Z A и подшипника X B , YB , силы тяжести стержней G 1, G 2, G 3 и силы инерции F1ин , F2ин показаны на рис. 16 а. Составим уравнения, вытекающие из принципа Даламбера: Yi 0; YA YB F1ин F2ин 0; Z i 0; Z A G3 G1 G2 0; 2 0; YB AB G1 0,5 l1 sin α F1ин ( AO l1 cosα) 3 ин G2 l1 sinα 0,5l2 F2 AO l1 cosα 0. Так как активные силы и силы инерции расположены в плоскости yAz, то X B X A 0. Из уравнения моментов M xi ~ 31 ~ 1 2 [m1 g 0,5l1 sin 30 m1ω2 0,5l1 sin 30 ( AO l1 cos30 ) AB 3 . 2 o G2 (l1 sin 30 0,5l2 ) m2ω (l1 sin 30 0,5l2 ) AOl1 cos30 ] YB Подставляя числовые данные, получим YB 9,5 кН . Из уравнений проекций YA YB F1ин F2ин YB m 1 ω 2 0,5 l1 sin 30 m 2 ω 2(l 1 sin 30 0,5 l 2) 10,6 кН; Z A G3 G1 G2 (m 3 m 1 m 2) g 98,1 Н. Чтобы определить реакцию RD стержня ND, рассмотрим силы, действующие на раму ODE (см. рис. 16 б). Для определения реакции достаточно составить уравнение моментов относительно точки О: M iO 0; F1ин h F2ин l1cosα RD l1cosα G1 0,5l1sinα G2 l1sinα 0,5l2 0 Подставляя все известные данные, получим RD 15,8 кН . Таблица 6 Схемы механических систем к заданиям №2 задание №1 задание №2 задание №3 задание №4 ~ 32 ~ продолжение табл. 6 задание №5 задание №6 задание №7 задание №8 задание №9 задание №10 задание №11 задание №12 ~ 33 ~ продолжение табл. 6 задание №13 задание №14 задание №15 задание №16 задание №17 задание №18 задание №19 задание №20 ~ 34 ~ продолжение табл. 6 задание №21 задание №22 задание №23 задание №24 задание №25 задание №26 задание №27 задание №28 ~ 35 ~ окончание табл. 6 задание №29 задание №30 Таблица 7 Данные для индивидуального задания №2 Номер задания 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 m1 m2 кг 20 25 40 20 30 40 20 50 20 8 20 13 20 20 20 75 100 30 240 40 70 100 10 60 50 80 50 70 20 50 l R см – – – – 15 – – 60 50 80 80 60 – – – 30 50 8 25 40 30 – 40 20 40 22 40 40 20 20 – 10 150 – 40 – 60 – – 10 120 30 – – 60 20 50 70 – 120 150 140 120 30 – 20 42 – 60 M, ω, Нм рад/с t1 , c – – – – – – – – – – – 10 16 – 8 – – 12 9 – – – 9 – – – – – 10 13 10 – – – – – – 15 200 – 50 – – – – – – – – 4 – – – – – – – – – – – 1,0 – – – – – – – – 30 – 25 – 30 4,0 10 20-0,1t – – – 5-0,1t – – – – – – – – 10 65 20 160 – – – – 30 6 15 124 20 217 – – – – 20 – 25 – 20 – 20 250 – – – – ~ 36 ~ φ 1, градус – 60 60 – – 30 60 – – – – – – – – – – – – – – – – – – – – – – – 4. Теоремы о движении центра масс и об изменении количества движения механической системы 4.1. Теорема о движении центра масс Теорема: центр масс механической системы движется как материальная точка, в которой сосредоточена масса всей системы и к которой приложены все внешние силы системы m aC Fke , k где m – масса всей системы; aC ускорение центра масс; F e k Fe – k главный вектор внешних сил. Дифференциальные уравнения движения центра масс системы: m xc Fxe ; myc Fye ; mzc Fze , где xc , yc , zc – координаты центра масс; Fxe , Fye , Fze – проекции главного вектора внешних сил на оси координат. Теорема имеет следствие: Если главный вектор всех внешних сил системы равен нулю, то скорость центра масс остается постоянной, причем, если начальная скорость равна нулю, то центр масс остается неподвижным. Пример. Гладкий клин 1 с углом α и массой m1 установлен на гладкую горизонтальную плоскость. На нем лежит груз 2 массы m2 , соединенный с грузом 3 массы m3 гибкой нерастяжимой невесомой нитью, перекинутой через невесомый блок. Найти перемещение клина по плоскости при опускании груза 3 на расстояние h, если в начальный момент система находилась в покое. Нить от вертикали не отклоняется. Решение. Устанавливаем, что при движении вдоль оси Ox имеет место следствие теоремы о движении центра масс: xC const . Обозначим через x1 перемещение клина по горизонтальной плоскости от начального положения. При опускании груза 3 на h груз 2 поднимется по наклонной плоскости клина на такое же расстояние, так как ~ 37 ~ нить нерастяжима (на рис. 17 система изображена в конечном положении, когда груз 3 опустился на расстояние h). Груз 3 переносится платформой вдоль оси Ox на расстояние x3 x1 . Абсолютное перемещение груза 2 вдоль оси Ox равно: x2 h cosα x1 . Тогда, согласно условию xc=const: xc m1x1 m2 (h cosα x1 ) m3x1 0 , откуда m2 x1 h cosα m1 m2 m3 Знак минус показывает, что клин переместился влево вдоль оси Ox. 4.2. Количество движения материальной точки и системы. Импульс силы Количеством движения материальной точки называется векторная величина, равная произведению массы точки на вектор ее скорости. Направление вектора количества движения совпадает с направлением вектора скорости. Единица измерения в СИ – 1 кг м с . Количеством движения механической системы называется векторная величина, равная геометрической сумме количеств движения всех ее точек: n Q mV i i . i 1 Количество движения механической системы удобно вычислять по формуле: Q mVC ; здесь m – масса системы, VC скорость ее центра масс. Элементарным импульсом силы называется векторная величина dS , равная произведению вектора силы F на элементарный промежуток времени ее действия dt: dS F dt . Импульс силы за конечный промежуток времени t1 равен определенному интегралу от элементарного импульса, взятому в пределах от нуля до t1 : t1 S F dt . 0 ~ 38 ~ В частном случае, если сила постоянна по модулю и направлению ( F =const), то S F t1 . Единица измерения импульса силы в СИ – 1 H c 1 кг м с . 4.3. Теорема об изменении количества движения механической системы Теорема об изменении количества движения системы в дифференциальной форме: производная по времени от количества движения системы равна геометрической сумме всех действующих на систему внешних сил: dQ Fke . dt В проекциях на оси координат: dQy dQx dQz Fkxe , Fkye , Fkze . dt dt dt Теорема об изменении количества движения системы в интегральной форме: изменение количества движения системы за конечный промежуток времени равно сумме импульсов внешних сил,действующих на систему, за тот же промежуток времени: Q1 Q0 Ske . В проекциях на оси координат: Q1x Q0 x Skxe , Q1 y Q0 y Skye , Q1z Q0 z Skze . Из того, что Q mVC , следует, что теорема о движении центра масс и теорема об изменении количества движения системы представляют собой две разные формы одной теоремы. Следствием теоремы является закон сохранения количества движения. 1. Пусть сумма внешних сил системы равна нулю: Fke 0 ; тогда из теоремы об изменении количества движения системы в дифференциальной форме следует, что при этом Q const . Если главный вектор внешних сил системы равен нулю, то вектор количества движения системы остается постоянным по модулю и направлению. 2. Пусть сумма проекций внешних сил на какую-нибудь ось (например, Оx) равна нулю: Fkxe 0 ; тогда Qx const . ~ 39 ~ Если сумма проекций всех внешних сил на какую-нибудь ось равна нулю, то проекция количества движения системы на эту ось есть величина постоянная. Внутренние силы не могут изменить количество движения системы. Контрольные вопросы 1. Сформулируйте теорему о движении центра масс системы. 2. Влияют ли внутренние силы системы на движение ее центра масс? На ее количество движения? 3. При каких условиях центр масс системы находится в покое? Движется равномерно и прямолинейно? 4. Как влияют на движение центра масс системы приложенные к ней пары сил? 5. Чему равны количества движения материальной точки и системы? 6. Чему равно количество движения тела, вращающегося вокруг неподвижной оси, проходящей через его центр масс? 7. Как определяются элементарный импульс силы и импульс силы за конечный промежуток времени? 8. Сформулируйте теорему об изменении количества движения механической системы в дифференциальной и интегральной формах. 9. В каких случаях количество движения механической системы или его проекции на оси остаются постоянными? Таблица 8 Тестовые задания № Задание/ответ Схема Масса механической системы m 5 кг . Проекции ускорения 1 центра масс аСх 5 м/с 2 , аСу 2 м/с 2 , аСz 7 м/с 2 . Модуль главного вектора внешних сил F ... H . Ответ: 30 2 Материальная точка движется по закону x 4 t 2 м под влиянием сил F1 F3 4 Н, F2 20 Н . Масса точки равна m ... кг . Ответ: 2 ~ 40 ~ окончание табл. 8 3 4 Центр масс системы массой m 5 кг движется прямолинейно по закону SC (20t 5) м . Модуль количества движения системы Q ... кг м/с . Ответ: 100 Сила изменяется по закону F 4t H ; за время от t 0 до 0 t 3 c импульс силы равен S ... Н с . 1 Ответ: 18 5 Масса груза m 8 кг , скорость движения груза V (3 i 4 j ) (м/с) . Проекция количества движения на ось Оу Qу ... кг м/с . Ответ: 32 5. Теорема об изменении кинетического момента 5.1. Кинетический момент механической системы Кинетическим моментом материальной точки относительно некоторого центра О называется векторное произведение r mV , где r радиус-вектор движущейся точки, проведенный из центра О. Кинетическим моментом (главным моментом количеств движения) системы относительно центра О называется геометрическая сумма кинетических моментов всех точек системы относительно того же центра n n k 1 k 1 Ko M O mkVk rk mkVk , где rk радиус-вектор k-ой точки, проведенный из точки O; mkVk – количество движения k-ой точки. Кинетический момент относительно неподвижной точки при произвольном движении системы K0 KСr ρС mVC , ~ 41 ~ где K Сr – кинетический момент в относительном движении вокруг центра масс; ρС – радиус-вектор центра масс, проведенный из точки O; mVC – количество движения системы. Кинетический момент относительно оси вращения твердого тела K z J z ωz . Здесь J z – момент инерции тела относительно оси вращения; ω z – проекция угловой скорости на ось вращения (алгебраическая угловая скорость). Кинетический момент вращающегося тела относительно оси вращения равен произведению момента инерции тела относительно этой оси на угловую скорость тела. Кинетический момент тела относительно неподвижной точки A при движении в плоскости материальной симметрии OXY K A M A mVC J zcωz m xC yC xC yC J zc ωz , где xС , yС – координаты центра масс; J zc момент инерции тела относительно центральной оси, перпендикулярной плоскости движения; m – масса тела. 5.2. Теорема об изменении кинетического момента относительно неподвижной точки и центра масс системы Теорема: производная по времени кинетического момента системы относительно неподвижного центра А равна сумме моментов внешних сил системы относительно того же центра. d KA M A Fke . dt При замене неподвижного центра А на центр масс С вид уравнения сохраняется: dKC M C Fke . dt При этом центр масс может быть движущейся точкой. Теорема имеет следствия. 1. Если сумма моментов относительно какого-нибудь неподвижного центра действующих на систему внешних сил равна нулю, то кинетический момент относительно этого центра постоянен по модулю и направлению, т.е. если M A ( Fke ) 0 , то K A const . ~ 42 ~ 2. Если сумма моментов внешних сил относительно какой-либо неподвижной оси равна нулю, то кинетический момент системы относительно этой оси будет величиной постоянной, т.е. если M x ( Fke ) 0 , то K x const . Эти следствия представляют собой закон сохранения кинетического момента системы. 3. Из уравнения, выражающего теорему, видно, что внутренние силы не могут изменить кинетический момент системы. Пример. При пуске в ход электрической лебедки к ее барабану приложен вращающий момент mвр bt , где b постоянная. Груз массы m1 поднимается посредством каната, навитого на барабан радиуса r и массы m2 . Определить угловую скорость барабана, считая его сплошным однородным цилиндром. В начальный момент лебедка находилась в покое. Решение. Рассматриваем барабан, канат и груз как одну материальную систему. Вводим систему координат, как показано на рис. 18, направляя ось Oz по оси вращения барабана. Внешними активными силами этой системы будут силы тяжести барабана и груза m2 g , m1 g и вращающий момент mвр , реакции внешних связей X и Y . Записываем теорему об изменении кинетического момента относительно оси Oz: dK z / dt M ze ; M ze mвр m1gr . Кинетический момент системы: K z K1z K 2 z mz (mV 1 ) J 2zω mVr J 2 z ω mVr (m2 r 2 / 2)ω, 1 1 где K1z момент количеств движения груза, движущегося поступательно, K 2 z кинетический момент барабана, вращающегося вокруг неподвижной оси, а J 2 z его момент инерции относительно той же оси, равный для сплошного однородного цилиндра m2r 2 / 2 . ~ 43 ~ Учитывая, что V ωr , имеем: K z (m1 m2 / 2)r 2ω . Применяя теорему, получаем дифференциальное уравнение движения системы: d m (m1 2 )r 2ω mвр m1gr ; dt 2 dω 2(bt m1 gr ) . dt (2m1 m2 )r 2 Разделяем переменные и интегрируем: 2b 2m1gr dω tdt dt ; (2m1 m2 )r 2 (2m1 m2 )r 2 bt 2 2m1grt ω C1 . 2 (2m1 m2 )r (2m1 m2 )r 2 Подставляя в последнее выражение начальные условия (при t 0 , ω(0) ω0 0 ), находим C1 0 . Угловая скорость барабана: bt 2m1 gr ω t. (2m1 m2 )r 2 Контрольные вопросы 1. Чему равен кинетический момент материальной точки относительно центра? 2. Будет ли изменяться кинетический момент относительно неподвижного центра тела, движущегося поступательно, прямолинейно и равномерно? 3. Чему равен кинетический момент твердого тела относительно оси вращения? 4. Сформулируйте теорему об изменении кинетического момента системы. 5. Можно ли за счет внутренних сил изменить кинетический момент механической системы? 6. В каких случаях кинетический момент механической системы относительно центра или его проекция на заданную ось остаются постоянными? ~ 44 ~ Таблица 9 Тестовые задания № Задание/ответ 1 Момент инерции диска относительно точки O J 0 4 кг м 2 . Кинетический момент диска относительно оси Oz K z ... кг м/с2 . Ответ: 20 2 Кинетический момент пластины ABC относительно оси z K z 8t кг м/с2 . Модуль главного вектора моментов внешних сил относительно оси z M ... Н м . Ответ: 8 3 Массы грузов m1 4 кг , m2 2 кг соответственно. Масса блока равна нулю. Модуль кинетического момента системы относительно точки C KC ... кг м/с2 . Ответ: 120 4 Кинетический момент системы относительно центра C KC 25t 2 кг м/с2 . В момент времени t1 2 с величина момента M ... Н м . Ответ: 20 ~ 45 ~ Схема окончание табл. 9 5 Масса однородного стержня m 3 кг , длина l 0,4 м . Кинетический момент относительно оси Oz K z 3,2 кг м/с2 . Угловая скорость вращения ωz рад с . Ответ: 20 6. Теорема об изменении кинетической энергии 6.1. Работа и мощность силы Элементарная работа силы d A F dr Fτ dS F dS cosα , где Fτ проекция силы на направление перемещения точки приложения силы; α угол между направлениями силы и перемещения. Работа переменной силы на конечном перемещении A Fτ dS F cosα dS . S S Элементарная работа пары сил (момента) d A M Z dφ , где M Z проекция момента пары сил на ось вращения; dφ положительное приращение угла поворота тела. Работа пары сил на конечном повороте тела φ A M Z dφ . φ0 Работа пары сил с постоянным моментом M Z const A MZ φ, где φ угол поворота тела в положительном направлении. Мощность силы N F V F V cosα , где α угол между направлениями силы и скорости точки приложения силы. Мощность пары сил (момента) N M Z ωZ , где ω z проекция угловой скорости на ось вращения. ~ 46 ~ 6.2. Кинетическая и потенциальная энергия Кинетической энергией материальной точки называется скалярная величина, равная mV 2 / 2 . Кинетической энергией механической системы называется сумма кинетических энергий всех ее материальных точек: mkVk2 Т . 2 Кинетическая энергия при вращательном движении тела 1 T J z ω2 , 2 где J z момент инерции тела относительно оси вращения; ω угловая скорость тела. Кинетическая энергия при плоском движении тела 1 1 T mVC2 J zC ω2 , 2 2 m V где масса тела; C скорость центра масс; J zC момент инерции относительно оси, проходящей через центр масс перпендикулярно плоскости движения; ω угловая скорость тела. Область пространства, в которой на помещенную туда точку действует сила, не зависящая от времени, называется стационарным силовым полем. Стационарное силовое поле называется потенциальным, если существует такая функция координат П x, y, z , называемая потенциальной энергией, что проекции силы могут быть представлены через нее следующим образом: П П П Fx , Fy , Fz . x y z Потенциальная энергия определяется с точностью до постоянного слагаемого. Потенциальная энергия равна работе потенциальной силы при переходе из текущего положения M в начальное положение M 0 , в котором она равна нулю ( F ) A( F ) . Потенциальная энергия тяжелого тела в поле силы тяжести в случае, когда ось Oz направлена вверх П mgz , где m масса; g ускорение свободного падения; z координата центра тяжести. ~ 47 ~ λ2 . 2 Здесь c жёсткость пружины; λ удлинение (укорочение). П 0 при недеформированном положении пружины. Если в потенциальном силовом поле движется система материальных точек, то потенциальная энергия этой системы равна сумме потенциальных энергий всех точек системы, то есть i ( xi , yi , zi ) . Следовательно, работа потенциальных сил системы A A( Fi ) 0 ( Fi ) ( Fi ) 0 . Работа силы по любому замкнутому контуру в потенциальном силовом поле равна нулю. Потенциальная энергия пружины П c 6.3. Теорема об изменении кинетической энергии Теорема об изменении кинетической энергии в интегральной форме: изменение кинетической энергии механической системы при ее переходе из начального положения в текущее положение равно сумме работ внешних и внутренних сил системы, совершенных при этом переходе. T T0 Ake Aki , где Ake и Aki суммы работ внешних и внутренних сил; T0 начальная кинетическая энергия системы. Теорема об изменении кинетической энергии механической системы в дифференциальной форме: производная по времени кинетической энергии системы равна сумме мощностей внутренних и внешних сил системы. dT N ke N ki , dt и N ki суммы мощностей внешних и внутренних сил. Теорема в дифференциальной форме удобна для составления дифференциальных уравнений движения. При практическом применении теоремы нужно помнить о том, что кинетическую энергию следует вычислять в абсолютном движении. В частном случае, когда все внешние и внутренние силы системы потенциальны, имеет место закон сохранения полной механической энергии: если все внешние и внутренние силы механической системы являются потенциальными, то полная механическая энергия системы в где N e k ~ 48 ~ процессе движения остается постоянной величиной, равной своему начальному значению. T T0 0 , или T h , где h постоянная, равная начальному значению T0 0 полной механической энергии системы материальных точек. Механические системы, в которых выполняется закон сохранения полной механической энергии, называются консервативными. Консервативными называются в этом случае и силы системы и потенциальное силовое поле, где происходит движение системы. Пример. Груз A массы m1 приводит в движение каток B массы m2 посредством невесомой нерастяжимой нити, перекинутой через блок С массы m3 (см. рис. 19 а). Считая блок и каток сплошными однородными цилиндрами, определить ускорение груза. Качение катка происходит без скольжения, а трением качения катка и трением в оси блока можно пренебречь. Решение. Поскольку требуется определить ускорение, применяем теорему об изменении кинетической энергии в дифференциальной форме: dT dt Nke N ki . Все тела системы твердые, нить нерастяжима, поэтому N i k 0. Кинетическая энергия этой системы T T1 T2 T3 , где T1 , T2 и T3 кинетические энергии груза, катка и блока соответственно. ~ 49 ~ Груз движется поступательно: 1 2 T1 mV 1 1 . 2 Движение катка плоское: T2 12 m2VC22 12 J C2 ω22 , где VC2 скорость центра масс C2 катка, J C2 момент инерции катка относительно оси, проходящей через его центр масс перпендикулярно плоскости рисунка, ω2 угловая скорость катка. Блок вращается вокруг неподвижной оси, его кинетическая энергия: T 21 J 3 32 , где J 3 момент инерции блока относительно оси вращения, ω3 угловая скорость блока. Моменты инерции катка и блока: J C2 12 m2r22 ; J 3 12 m3r32 , где r2 и r3 радиусы катка и блока. Таким образом: 2 2 2 2 2 2 1 1 1 T 12 mV 1 1 2 m2VC2 4 m2 r2 ω2 4 m3r3 ω3 . Чтобы сократить число неизвестных, используем уравнения связей. Нить нерастяжима, поэтому скорость точки D на ободе блока равна скорости груза, а скорость точки E блока равна скорости точки L катка; находим: ω3 V1 / r3 . Мгновенный центр скоростей P катка находится в точке касания катка с неподвижной плоскостью, каток вращается с угловой скоростью ω2 VL LP V1 2r2 , а центр масс C2 катка движется вправо со скоростью VC2 0,5VL V1 2 . Учитывая последние соотношения, имеем 1 1 1 1 1 2 2 T mV m2V12 m3V12 (8m1 3m2 2m3 )V12 . 1 1 m2V1 2 8 16 8 16 На систему действуют внешние силы: m1g , m2 g , m3 g силы тяжести тел, R реакция подшипников блока, Fт и N 2 составляющие реакции шероховатой поверхности, возникающие в точке касания катка с поверхностью. ~ 50 ~ Мощности сил m3 g и R равны нулю, так как точка их приложения неподвижна. Силы Fт и N 2 приложены в мгновенном центре скоростей P катка, их мощность равна нулю, так как VP 0 . Мощность силы m2 g равна нулю, так как m2 g VC2 . Следовательно, Nke m1g V1 m1gV1. Подставляя полученные значения кинетической энергии и мощности в формулу dT dt Nke Nki , имеем: dV1 8m1 3m2 2m3 d 8m1 3m2 2m3 2 m1gV1 . V1 m1 gV1 ; 2V1 dt 16 dt 16 Сокращая обе части последнего выражения на V1 , учитывая, что dV1 / dt a1 , получаем m1 a1 (m1 83 m2 14 m3 ) m1g ; a1 g 3 1 m1 m2 m3 8 4 Контрольные вопросы 1. Что называется кинетической энергией механической системы? 2. Запишите формулы для вычисления кинетической энергии твердого тела при поступательном, вращательном и плоскопараллельном движении. 3. Что называется элементарной работой силы F на бесконечно малом перемещении d r ? 4.Как вычисляется работа переменной силы на конечном перемещении по траектории? 5. Как вычисляется работа силы тяжести? 6. Как вычисляется работа момента силы? 7.Какое силовое поле называется потенциальным? 8. Что называется потенциальной энергией? 9.Как связана потенциальная энергия с работой потенциальной силы? 10. Сформулируйте теорему об изменении кинетической энергии механической системы. 11. Сформулируйте закон сохранения полной механической энергии. 12. Как вычисляется мощность силы и момента? ~ 51 ~ Таблица 10 Тестовые задания Задание/ответ № 1 Схема Стержень AB невесом, P2 5 H . После опускания ползуна 1 весом на расстояние P1 4 H AO 2 м силы совершат работу A ... Дж . Ответ: 8 Момент инерции барабана J 2 кг м 2 , ω 4 рад/с , R 1м , 2 3 масса груза m P / g 2 кг . Кинетическая энергия системы … Дж. Ответ: 32 Вращающий момент на валу двигателя ω 300 рад/с . Мощность момента N ... кВт . M 20 Н м , Ответ: 6 4 При повороте колеса 3 на 6 рад момент M и сила P 2 H совершат работу A ... Дж . Ответ: 84 ~ 52 ~ окончание табл. 10 5 Материальная точка весом P 4 H поднялась по дуге окружности из точки A в точку B . Потенциальная энергия увеличилась на … Дж. Ответ: 24 6 Кинетическая энергия материальной точки возросла с 10 до 70 Дж. Силы, действующие на точку, совершили работу A ... Дж . Ответ: 60 7 При опускании стержня до вертикального положения из горизонтального состояния покоя он приобретёт угловую скорость ω ... рад/с . Ответ: 5 g . Кинетическая энергия однородного диска весом P 20 H равна 8 T 6ω2 Дж . Угловое ускорение ε 6 рад/с2 . Сила F ... H . Ответ: 28 ~ 53 ~ Индивидуальное задание №3 Теорема об изменении кинетической энергии механической системы (интегральная форма) Механическая система под действием сил тяжести приходит в движение из состояния покоя; начальное положение системы показано на схемах в таблице 11. Учитывая трение скольжения тела 1 (варианты 1–3, 5-8, 10-12, 14, 19–23, 25-28, 30) и сопротивление качению тела 3, катящегося без скольжения (варианты 2, 4-7, 9–11, 13, 15–18, 20, 22–24, 26, 27, 29), определить скорость тела 1 в тот момент, когда пройденный им путь станет равным S . В задании приняты следующие обозначения: массы тел 1, 2, 3, 4 – m1, m2 , m3 , m4 ; радиусы инерции ρ2 , ρ3 , ρ4 , тел 2, 3, 4 относительно горизонтальных осей, проходящих через их центры тяжести; радиусы больших и малых окружностей – R2 , r2 , R3 , r3 , R4 , r4 ; f коэффициент трения скольжения; δ коэффициент трения качения. Необходимые для решения данные приведены в таблице 12. Во всех вариантах m1 10m . Блоки и катки, для которых радиусы инерции в таблице не указаны, считать сплошными однородными цилиндрами. В варианте 17 тележка 4 на четырёх одинаковых колёсах 3 . Наклонные участки нитей параллельны соответствующим наклонным плоскостям. Пример выполнения задания. Дано: m1 масса груза 1, m2 2m1, m3 m1, m4 0,5m1, m5 20m1 ; r2 0,5R2 , R2 R3 12 см , r3 0,75R3 , R5 20 см , AB l 4R3 , ρ2 8 см , ρ3 10 см , f 0,1 ; δ 0,2 см , S 0,06π м . Механическая система под действием сил тяжести показана в начальном положении (рис. 20). Сопротивление качению тела 2 не учитывать. Шатун 4 считать тонким однородным стержнем; каток 5 – однородный сплошной цилиндр. Массами звена BC5 и ползуна B пренебречь. ~ 54 ~ Требуется определить скорость груза 1 V1 в конечном положении. Решение. Применим теорему об изменении кинетической энергии системы: T T0 Ake Aki , (1) где T0 и T кинетическая энергия системы в начальном и конечном положениях; A A e k сумма работ внешних сил, приложенных к системе; сумма работ внутренних сил системы. Для систем, состоящих из абсолютно твёрдых тел, соединённых нерастяжимыми нитями, Aki 0 . Так как в начальном положении система находится в покое, то T0 0 . Уравнение (1) принимает вид: (2) T Ake . i k Кинетическая энергия T системы в конечном её положении (рис. 21) равна сумме кинетических энергий тел 1, 2, 3, 4, 5: T T1 T2 T3 T4 T5 . (3) Кинетическая энергия груза 1 T1 m1 V12 . (4) 2 Кинетическая энергия катка 2, совершающего плоское движение: m2 VC22 J 2 ω22 T2 , (5) 2 2 где VC2 скорость центра тяжести C2 катка 2, (6) VC2 V1 , J 2 момент инерции катка 2 относительно его центральной оси C2 : ~ 55 ~ J 2 m2 ρ22 , (7) ω2 угловая скорость катка 2. Так как каток катится без скольжения, то мгновенный центр скоростей катка находится в точке P2 . Поэтому: VC V ω2 2 1 . (8) C2 P2 R2 Подставляя (6) – (8) в формулу (5), получаем m2 V12 m2ρ22V12 1 ρ22 2 T2 m2 1 2 V1 . (9) 2 2 R22 2 R2 Кинетическая энергия звена 3, вращающегося вокруг неподвижной оси Ox : J 3 x ω 32 , (10) T3 2 где J 3x момент инерции звена 3 относительно оси Ox : (11) J 3 x m3ρ32x , ω3 угловая скорость звена 3: V ω3 E . (12) r3 Скорость точки E звена 3 равна скорости точки D катка, которую можно найти из соотношения: (r R 2 ) VD , 2 VC2 R2 а так как VC2 V1 , R2 2 r 2 , то: VD 3 3 , VE VD V1 . (13) V1 2 2 Подставляя (13) в (12), получаем 3 V ω3 1 . (14) 2 r3 После подстановки (11) и (14) в (10) выражение кинетической энергии звена 3 принимает вид: 2 m3 ρ 32 x 3V1 9 ρ 32x V 12 . (15) T3 или T3 m3 8 r 32 2 2r3 Кинетическая энергия шатуна 4, совершающего плоское движение: ~ 56 ~ 1 1 m 4 V C2 4 J 4ω 42 , 2 2 где VC4 скорость центра тяжести C 4 шатуна 4, J 4 момент инерции шатуна относительно центральной оси C4 , ω4 угловая скорость шатуна 4. Для определения скорости VC4 и угловой скорости ω 4 найдём конечное положение шатуна 4. Когда груз 1 пройдёт путь s 0,06 π (м), барабан 3 повернётся на угол φ3 . Этот угол можно определить на основании формулы (14), заменяя в ней dφ3 dS ω3 , V1 dt dt Получаем dφ3 3 dS 3 dS , или dφ3 ; dt 2r3 dt 2 r3 после интегрирования (при нулевых начальных условиях) 3 S φ3 . 2 r3 Видно, что линейные и угловые перемещения находятся в такой же зависимости, как соответствующие линейные и угловые скорости. Вычислим угол 3 0,06 π φ3 π. 2 0,09 T4 Значит, барабан 3 повернётся на 180o ; при этом шатун 4 из начального положения A0 B0 перейдёт в конечное положение AB (см. рис. 21). Так как скорости точек А и В шатуна в этот момент параллельны, мгновенный центр скоростей шатуна находится в бесконечности. Угловая скорость шатуна 4 0 , а скорости всех его точек равны между собой. Кинетическая энергия шатуна 4 m 4 V C2 4 , (16) T4 2 где (17) VC4 VA . Скорость точки А звена 3 (18) VA ω 3 R 3 3 R V или с учётом (14) VA 3 1 . 2 r3 ~ 57 ~ Поскольку r 3 С учётом (17) 3 R 3 , получим VA 2 V1 . 4 (19) VC4 2 V1 . После подстановки (19) в (16) выражение кинетической энергии шатуна 4 принимает вид: 1 T 4 m 4 (2V 1) 2 2 m 4 V 12 . (20) 2 Кинетическая энергия катка 5 1 1 T 5 m 5 V C2 5 J 5 ω 52 , 2 2 где VC5 скорость центра тяжести C5 катка 5; J 5 момент инерции катка 5 (однородного сплошного цилиндра) относительно его центральной 1 оси C5 ; J 5 m 5 R 52 , ω 5 угловая скорость катка 5. 2 Так как каток катится без скольжения, то мгновенный центр скороV стей находится в точке P5 (см. рис. 21), поэтому ω 5 C 5 , R5 2 2 1 1 m5 R 5 V C5 3 2 T5 m5 V C5 m5 V C2 5 . 2 2 2 2R 5 4 Так как звено BC 5 совершает поступательное движение, то VC 5 VB ; но VB VC 4 2 V1 , т.е. VC5 2 V1 . Кинетическая энергия катка 5 принимает вид: 3 T5 m 5 (2 V1 ) 2 3 m 5V12 . (21) 4 По формуле (3) с учётом (4), (9), (15), (20), (21): m1 V 12 1 ρ 22 2 9 ρ 32x 2 T m 2 1 2 V 1 m 3 2 V 1 2 m 4V 12 3 m 5V 12 . 2 2 R2 8 r3 Подставляя сюда заданные значения масс и радиусов, получаем m 1V 12 . (22) T 129 2 Найдём сумму работ всех внешних сил, приложенных к системе, на заданном её перемещении. Покажем внешние силы (см. рис. 22). Работа силы тяжести G 1 : A G 1 G 1 h1 m1 g S sin α . (23) ~ 58 ~ Работа силы трения скольжения Fтр A Fтр Fтр S . Так как Fтр fN1 fG 1 cosα , то: A Fтр f m1g S cos α . Работа силы тяжести G 2 : A G 2 G 2h C 2 m 2 g S sinα . (24) (25) Работа сил сцепления Fсц 2 , Fсц 5 катков 2 и 5 равна нулю, так как эти силы приложены в мгновенных центрах скоростей катков. Работа силы тяжести G 4 : A G 4 G 4h C 4 , где h C 4 вертикальное перемещение центра тяжести C 4 шатуна 4 из начального положения в его конечное положение h C 4 R 3 (рис. 23): AG 4 m 4 g R 3 . (26) Работа пары сил сопротивления качению катка 5: A MC M C φ 5 , (27) где M C δ N5 δ G5 – момент пары сил сопротивления качению катка 5, φ5 угол поворота катка 5. Так как каток 5 катится без скольжения, то угол его повороSC та φ5 5 , где SC5 перемещение центра тяжести катка 5. R5 Работу пары сил сопротивления качению вычислим, как сумму работ этой пары при качении катка 5 влево при повороте тела 3 на угол ~ 59 ~ π / 2 и качении вправо, когда тело 3 повернётся ещё на угол / 2 . Путь, пройденный центром тяжести C 5 катка 5, равен сумме перемещений ползуна B влево и вправо: SC5 2 B0 B . (29) Определим перемещение B0 B при повороте тела 3 на угол / 2 . За начало отсчёта координаты точки B выберем неподвижную точку К плоскости (см. рис. 23). При этом повороте тела 3 шатун из положения A0 B0 перейдёт в положение K B . Тогда B 0 B K B 0 K B , где K B 0 K O O B 0 R 3 A 0 B 0 2 A 0O 2 R 3 l 2 R 32 , K B A B l 4 R 3 . Следовательно, 4 R R B0 B R 3 l 2 R 32 l R 3 2 3 2 3 4 R 3 0,88 R 3 . (30) Подставляя (30) в (29), а затем в (28), находим полный угловой путь катка 5: R φ 5 1,76 3 . (31) R5 Работа пары сил сопротивления качению по (27): R A M C δ m 5 g 1,76 3 . (32) R5 Сумма работ внешних сил определится сложением работ, вычисляемых по формулам (23) – (26) и (32): R Ake m1gS sin α f m1gS cosα m2 gS sin α m4 gR3 δm5 g 1,76 R3 5 Подставляя заданные значения масс, получаем R δ 20 1,76 R Ake m1gS sin α f cosα 2sin α 2S3 R S 3 , 5 или (33) Ake 1,51m1gS . Приравняем значения T и и (33): 129 A e k , определяемые по формулам (22) m1 V12 1,51m1 g S , откуда 2 2 1,51g S 3,02 V1 9,81 0,06 0,2 м / с . 129 129 ~ 60 ~ Таблица 11 Схемы механических систем к заданиям №3 задание №1 задание №2 задание №3 задание №4 задание №5 задание №6 задание №7 задание №8 ~ 61 ~ продолжение табл. 11 задание №9 задание №10 задание №11 задание №12 задание №13 задание №14 задание №15 задание №16 ~ 62 ~ продолжение табл. 11 задание №17 задание №18 задание №19 задание №20 задание №21 задание №22 задание №23 задание №24 ~ 63 ~ окончание табл. 11 задание №25 задание №26 задание №27 задание №28 задание №29 задание №30 ~ 64 ~ Таблица 12 № варианта Данные для индивидуального задания №3 m2 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 5m 2,5m 20m 10m 5m 5m 20m 10m 14m 10m 20m 3m 20m 10m 20m 5m 5m 20m 5m 5m 2,5m 20m 5m 20m 5m 30m 5m 40m 30m 10m m3 m4 R2 R3 кг 3m m 5m 60m 10m 2m 50m m 20m 20m 10m m 30m m 2,5m 40m 50m 50m 2m 2,5m 2,5m 20m 3m 10m 2m 10m 3m 2m 10m m ρ2 ρ3 20 16 12 12 12 18 16 16 12 20 15 15 18 18 26 26 20 12 14 12 - 18 16 25 16 18 25 15 15 25 25 18 20 20 - f δ , см S,м 0,12 0,2 0,2 0,1 0,15 0,15 0,1 0,2 0,1 0,15 0,1 0,2 0,17 0,1 0,12 0,15 0,1 0,1 0,22 0,1 0,1 0,2 0,2 0,2 0,2 0,2 0,25 0,32 0,2 0,2 0,2 O,25 0,2 0,24 0,2 0,25 0,2 0,2 0,28 0,2 0,2 - 2 2,4 2 2 1 1 1,2 1 1,2 1,2 1,5 1,5 3 1 1 1,5 2 2 2,5 2,5 3 1,5 1,75 2 1 1,5 2 2 2 2 см 15m 2,5m 5m 8m 8m 10m 20m 2m m 5m 40m 20m 10m 2m 2,5m 13m 20m 10m 26 20 16 15 16 20 20 20 16 24 20 20 20 20 30 30 30 16 16 15 - 20 35 18 20 30 20 20 20 20 30 20 20 20 15 25 20 30 30 24 25 20 28 30 20 - ~ 65 ~ Индивидуальное задание №4 Теорема об изменении кинетической энергии механической системы (дифференциальная форма) Для заданной механической системы определить ускорения грузов и натяжения нитей, к которым прикреплены грузы. Система движется из состояния покоя. Варианты механических систем представлены в таблице 13, а необходимые для решения данные приведены в таблице 14. Во всех вариантах m1 2m, m 10 кг . Блоки и катки, для которых радиусы инерции в таблице не указаны, считать сплошными однородными цилиндрами. Примечания: Радиусы инерции вычислены относительно центральных осей. Коэффициент трения принимать одинаковым, как при скольжении тела по плоскости, так и при торможении колодкой (варианты 9; 11). Пример выполнения задания. Дано: Схема механической системы (рис. 24) m1 m2 2m, m3 m4 m , R 2r , ρ2 r 2, f 0,2 . Блок 3 – однородный цилиндр. Определить ускорения грузов и натяжения ветвей нити 1– 2 и 3–4. Решение. Применим к решению задачи теорему об изменении кинетической энергии в дифференциальной форме dT N . dt Целесообразно определить истинное направление движения системы, чтобы правильно показать направление сил трения. В рассматриваемом примере груз 1 опускается. Покажем активные силы: силы тяжести G1, G2 , G3 , G4 , а также составляющие реакции плоскости Rn и Fтр (см. рис. 25). Сила трения: Fтр f Rn f G1 cos60о f G . Покажем линейные и угловые скорости и составим уравнения связей. Мгновенный центр скоростей блока 3 находится на одной вертикали с центром блока 2. Расстояние между МЦС и центром блока 3 (см. рис. 25, б): ~ 66 ~ 3 r b rr . 2 2 Находим: V V ω 2 ω3 1 1 , R 2r V V3 V4 ω3b 1 . 4 Кинетическая энергия системы равна сумме кинетических энергий звеньев механизма: T T1 T2 T3 T4 . Грузы 1 и 4 движутся поступательно: 1 1 1 2 2 m4V42 mV12 . T1 mV 1 1 mV1 ; T4 2 2 32 Блок 2 вращается вокруг неподвижной оси: 1 T2 J 2ω22 , 2 1 момент инерции блока 2 J 2 m2ρ22 , следовательно: T2 mV12 . 2 Блок 3 совершает плоское движение: 1 1 T3 m3V32 J 3ω32 , 2 2 1 9 J 3 m3 R32 mr 2 , следовательно: момент инерции блока 3 2 8 11 T3 mV12 . 64 Кинетическая энергия системы: 1 3 1 T mV12 mV12 mV12 mV12 , 2 64 32 109 T mV12 . 64 Определим мощность сил, действующих на систему. Мощность силы G2 , приложенной в неподвижной точке, и мощность реакций идеальных связей равна нулю. Мощность остальных сил N G1 sin60o V1 Fтр V1 G3 V3 G4 V4 . Учитывая значение силы Fтр , уравнения связей и исходные данные, находим ~ 67 ~ N 1,03mgV . 1 dT 109 dT mV1 a1 , значения и N dt 32 dt 109 mV1 a1 1,03mgV1 , находим: подставляем в уравнение теоремы 32 a1 2,97 м/с2 . Дифференцируя по времени уравнение связи V4 V1 4 , находим: a4 a1 4 ; a4 0,74 м/с2 . Для определения натяжения нити на участке 1 – 2 мысленно рассечем нить и заменим ее действие на груз 1 реакцией S12 (рис.26, а). Применим теорему об изменении кинетической энергии в дифференциdT альной форме: 1 N1 . dt Кинетическая энергия найдена ранее: T1 mV12 . Мощность сил N1 G1sin60o V1 Fтр V1 S12 V1 . Получим: 2mV1 a1 G1sin60o Fтр S12 V1 , Вычисляем производную откуда: S12 G1sin60o Fтр 2ma1 ; S12 0,93G . Для определения усилия на участке 3 – 4 мысленно выполняем рассечение и вводим реакцию S34 (рис. 26, б). 1 Кинетическая энергия T4 mV12 . 32 Мощность сил N S34 V4 G4 V4 . Применяем теорему: 1 V mV1 a 1 S34 G4 1 . 16 4 Находим 1 S34 ma1 G ; 4 S34 1,08G . ~ 68 ~ Таблица 13 Схемы механических систем к заданиям №4 задание №1 задание №2 задание №3 задание №4 задание №5 задание №6 задание №7 задание №8 ~ 69 ~ продолжение табл. 13 задание №9 задание №10 задание №11 задание №12 задание №13 задание №14 задание №15 задание №16 ~ 70 ~ продолжение табл. 13 задание №17 задание №18 задание №19 задание №20 задание №21 задание №22 задание №23 задание №24 ~ 71 ~ окончание табл. 13 задание №25 задание №26 задание №27 задание №28 задание №29 задание №30 ~ 72 ~ Таблица 14 Данные для индивидуального задания №4 № массы звеньев m2 m3 m4 R r 1 m 3m – 2 m m 3 m 4 5 6 7 8 9 10 11 12 13 Радиусы инерции f Дополнительные данные ρ2 ρ3 2 r 2 – – – 2 r 2 – – m – 2 r 2 – 0,1 m 4m – – – – 0,2 m m m 2r m 2m m 2m m 2m m 2m 2m m m 2m m 2m – – – – – 0,2m 0,2m 3 3 3 3 3 4 3 3 – 0,2 0,2 0,2 0,2 0,4 0,2 0,2 2m m 2m – r2 2 – – – – – – – – 2r3 – r2 2r3 ; R2 R3 14 2m m 4m – r2 2 2r3 – r2 2r3 ; R3 1,5R2 15 m 2m 2m – r2 2 2r3 – r2 2r3 ; R3 1,5R2 16 m 2m 4m – r2 2 2r3 – r2 2r3 ; R3 1,5R2 17 m m 2 0,1 0,2m 0,1m 0,3m 0,2m 6m 2 3 r 2 – – 18 19 – 0,3m 0,4 0,1 r3 1,2r; R3 1,2r3 20 0,2m 0,1m 6m 2 2r 1,6 r – 1,2 r r 2 0,2 r2 1,5r; R2 1,2r2 21 4m 0,2m – 3 – r 2 – 22 0,4m 0,6m – 2 – r 2 – 23 0,4m 0,2m – 1,5 1,2 r – – m m 8m – – – – 25 m 2m m – – – – R3 R2 26 2m 2m – – – – – R2 R3 27 2m 2m 8m 2 r 2 r 2 – 28 m m – 2 r 2 – 0,1 29 m m m 2 – – 30 m m 6m – – r 2 – 24 2r 2r 2r 2r – 2r 2r ~ 73 ~ 0,1 R2 R3 R3 1,2r Массы четырех колес одинаковы 4 3 7. Аналитическая статика 7.1. Связи Связями в аналитической механике называются ограничения, накладываемые на координаты и скорости точек несвободной механической системы. Связи, налагающие ограничения, которые сохраняются при любом положении механической системы, называются удерживающими. Связи, от которых система может освободиться, называются неудерживающими. Удерживающие связи математически выражаются уравнениями, неудерживающие – неравенствами. Связи, не изменяющиеся с течением времени, называются стационарными, изменяющиеся – нестационарными. В уравнения нестационарных связей явно входит время t. Связи, налагающие ограничения только на координаты точек системы, называются геометрическими, а налагающие ограничения еще и на скорости – кинематическими или дифференциальными. Кинематическую связь, которую интегрированием можно свести к геометрической, называют интегрируемой. К голономным относятся все геометрические связи, а также те дифференциальные связи, которые путем интегрирования могут быть сведены к геометрическим. Дифференциальная связь, уравнение которой не может быть проинтегрировано, называется неголономной. Механическая система называется голономной, если все ее связи голономные, и неголономной, если хотя бы одна из ее связей является неголономной. В дальнейшем мы будем рассматривать системы с удерживающими голономными связями. Рассмотрим примеры. Пример 1. На две материальные точки наложена связь в виде жесткого, невесомого и нерастяжимого стержня длины l. Уравнение связи 2 2 2 x2 x1 y2 y1 z2 z1 l 2 , где x1 , y1 , z1 , x2 , y2 , z2 координаты точек. Связь удерживающая, стационарная, геометрическая, голономная. Пример 2. Две материальные точки соединены невесомой, нерастяжимой, абсолютно гибкой нитью длины l. Математическое описание связи: x2 x1 2 y2 y1 2 z2 z1 2 l 2 . ~ 74 ~ Знак «меньше» соответствует состоянию, когда нить не натянута. Связь неудерживающая. Пример 3. Колесо катится без скольжения по неподвижной поверхности. Уравнение связи: VO ωR или xO Rφ . Это дифференциальная связь, но уравнение интегрируется и приводится к виду: xO Rφ . Следовательно, эта связь голономная. 7.2. Виртуальные перемещения Виртуальным (возможным) перемещением механической системы называется такое мысленное малое перемещение δ r1 , ,δ rn ее точек из данного положения при неизменном времени, которое допускается связями. При стационарных связях виртуальные перемещения точек системы пропорциональны виртуальным скоростям этих точек: δ rA VA AP , δ rB VB BP где точка P мгновенный центр скоростей; δ rA и δ rB виртуальные перемещения точек A и B ; V A и VB виртуальные скорости этих точек. Числом степеней свободы механической системы называется число независимых виртуальных перемещений, которые можно сообщить системе. У механической системы с геометрическими связями число степеней свободы совпадает с числом независимых координат, определяющих положение системы. 7.3. Идеальные связи Работа силы на виртуальном перемещении точки ее приложения называется виртуальной работой силы: δ A F δr Fxδx Fy δy Fz δz . Связь называется идеальной, если сумма работ реакций связей на любом виртуальном перемещении системы равна нулю, то есть n δ A( R ) Ri δ ri 0 . i 1 ~ 75 ~ К идеальным связям относятся: 1) гладкие поверхности; 2) идеальные шарниры; 3) нерастяжимые стержни с шарнирами на концах, абсолютно гибкие нерастяжимые нити; 4) связь, обеспечивающая качение без скольжения; 5) внутренние связи в абсолютно твердом теле, в абсолютно гибкой нерастяжимой нити. 7.4. Принцип виртуальных перемещений Для равновесия механической системы с идеальными, стационарными, удерживающими, голономными связями необходимо и достаточно, чтобы сумма работ активных сил на любом виртуальном перемещении системы была равна нулю и скорости всех точек в начальный момент времени равнялись нулю. n F k 1 k δ rk 0, Vk 0 0 k 1, , n . Выразим виртуальные перемещения через виртуальные скорости: δ ri kVi ; получим принцип виртуальных скоростей: n F V i 1 i i 0. Для равновесия системы с идеальными стационарными, удерживающими, голономными связями необходимо и достаточно, чтобы мощность активных сил на любом виртуальном движении системы была равна нулю. Пример. На кривошип OA кривошипно-ползунного механизма действует пара сил с моментом M . Кривошип и шатун AB невесомые стержни длины l . Найти силу P , удерживающую механизм в равновесии, если на шарнир A действует сила Q (рис. 29, а). ~ 76 ~ Решение. К механизму приложены активные силы P и Q и пара сил с моментом M . Все связи механизма идеальны. Реакции идеальных связей на рисунке не показываем. Положение механизма определяется одним углом φ , следовательно, система имеет одну степень свободы. Решим задачу, используя принцип виртуальных скоростей. Сообщим системе виртуальное движение ω ,VA ,VB . Составляем уравнения связей. VA ω OA ωl . Связь между скоростями точек А и В шатуна найдем при помощи теоремы о проекциях скоростей: VA* cos 90o 2φ VB* cosφ ; cos 90o 2φ sin2φ 2sinφcosφ ; VB* 2ω* l sinφ . Составляем уравнение мощности, выражающее принцип виртуальных скоростей: N Mω QVA cos(Q ^ VA ) PVB cos( P ^ VB ) . Mω QVA cos(180 φ) PVB cos180 Mω QVA cosφ PVB 0 Здесь N виртуальная мощность сил системы. Подставляем в уравнение значения VA и VB : Mω Qωl cosφ 2Pωl sin φ 0 ; M Ql cosφ 2Pl sin φ 0 . Находим P M Q ctgφ . 2l sin φ 2 Контрольные вопросы 1. Какими должны быть связи в системах, условия равновесия которых устанавливает принцип возможных перемещений (возможных скоростей)? 2. Какие связи называются идеальными? 3. Какие связи называются стационарными? 4. Какие связи называются удерживающими? 5. Как формулируется принцип виртуальных перемещений? 6. Как записывается формула, выражающая принцип возможных скоростей? ~ 77 ~ Таблица 15 № Тестовые задания Задание/ответ Схема 1 Число степеней свободы механизма … Ответ: 2 2 Вес груза P 8 Н , подвижный блок невесом. При равновесии механизма сила упругости пружины Fупр ... Н . Ответ: 4 3 Вес груза P 6 Н , F 2 Н , AB 4 м 2 / 3 AC . При равновесии механизма момент M ... Н м Ответ: 12 4 AO 2 м , M 20 Н м . При равновесии механизма в показанном положении сила тяжести ползуна P ... Н . Ответ: 6 5 Положение механической системы определяется тремя независимыми координатами. Число степеней свободы системы … Ответ: 3 ~ 78 ~ окончание табл. 15 6 Радиус невесомого подвижного блока R 2 м ; при равновесии механизма момент M ... Н м . Ответ: 8 Индивидуальное задание № 5 Принцип виртуальных перемещений (скоростей) в применении к механизмам Схемы механизмов, находящихся под действием взаимно уравновешивающихся сил, представлены в таблице 16, а необходимые для решения данные приведены в таблице 17. Применяя принцип виртуальных перемещений (скоростей), определить величину, указанную в последней графе таблицы 17. Примечания. На схемах плоскость xOy ( xO1 y) горизонтальна; плоскость yOz ( yO1z ) вертикальна. В таблице 17 в столбце «Удлинение пружины» знаком «–» отмечено сжатие пружины. Пример выполнения задания. Дано: Схема механизма (см. рис. 30). Q 100 Н ; коэффициент жесткости пружины c 5 Н/см ; R2 40 см ; r2 20 см ; R3 10 см ; α 30 ; O3 A l 50 см ; β 90 . Определить удлинение h пружины, пренебрегая весом звеньев O3 A и АВ. Решение. Рассматриваемый механизм (см. рис. 30) находится под действием уравновешенной системы сил: силы упругости F , сил тяжести а также реакций опор. Направление силы F выбрано в предположении, что пружина сжата. Решим задачу, используя принцип возможных скоростей: Pi Vi 0 или Pi Vi cos( Pi ^ Vi ) 0 Сообщим звену 2 виртуальную угловую скорость ω2 (см. рис.30). Груз 1 получит вертикальную скорость VQ . Шестерня 3 вместе с жёстко соединённым с нею кривошипом O3 A приобретёт угловую скорость 3 . ~ 79 ~ Скорость точки К VK ω2 R2 ω3 R3 , ω3 ω2 Скорость груза R2 . R3 VQ ω2 r2 . Скорость точки А V A ω 3 O3 A . Для определения скорости точки В используем теорему о проекциях скоростей: VA VB cosα . Тогда R OA VB 2 3 ω2 . R3 cosα Составим уравнение мощностей: Q VQ F VB 0 . Здесь сила упругости пружины: F ch. Подставив в уравнение мощностей значения VQ ,VB , F , найдем: rRQ h 2 3 cosα . R2 l c Подставляя числовые значения величин, получим h 1,74 см . Знак «+» в числовом результате означает, что пружина сжата. ~ 80 ~ Таблица 16 Схемы механизмов к заданиям №5 задание №1 задание №2 задание №3 задание №4 задание №5 задание №6 задание №7 задание №8 ~ 81 ~ продолжение табл. 16 задание №9 задание №10 задание №11 задание №12 задание №13 задание №14 задание №15 задание №16 ~ 82 ~ продолжение табл. 16 задание №17 задание №18 задание №19 задание №20 задание №21 задание №22 задание №23 задание №24 ~ 83 ~ окончание табл. 16 задание №25 задание №26 задание №27 задание №28 задание №29 задание №30 ~ 84 ~ Таблица 17 Данные для индивидуального задания №5 Линейные размеры 1 2 ОА 10 см О1 А 20 см 3 4 5 R1 20 см, r2 30 см, R2 40 см 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 OC : OA 4 : 5 OA 100 см R1 15 см, R2 50 см, r2 20 см, О1 А 80 см OC OA OC AC OA 20 см R1 40 см, r1 15 см, R2 20 см, ОА 100 см OA 20 см O1D 60 см, АО 20 см OA 40 см OB 2 OA AC OC OD d1 80 см, l1 100 см, d 2 25 см, l2 75 см OA 20 см R1 20 см, R2 30 см, ОА 25 см ОА АВ АС 50 см ОА АВ АС СD 25 см OA 40 см ОС 2 ОА 100 см AD OD OB OD BD 0,8 AO OA 25 см ОВ АВ ОА 0,8 ОВ BD O1D; AO 30 см R1 36 см; r1 15 см; R2 20 см; r2 10 см Q – – P – 100 Момент, Нм M 20 – – – – – 200 – 100 – 10 – – – – -4 – Q C P 200 – – – – P – – 200 – 200 – – – – 10 10 – 3 2 – P Q M 2000 – – – 4 C – – – 20 3000 – – – – – 300 100 200 – – – – – 25 250 – – – 3 3 P P P P P 5000 – – 100 4 P – 200 – 50 – – – – 400 – – – – – 200 – 100 200 – 200 250 – 500 – 450 – 200 – 100 – – 400 50 – – 120 – – 120 – 100 – – – – 50 150 120 – 180 – 100 – – – – – – – 2,5 3 2 2 – – P h P M M P h Q P C P Q h – 600 – – – Q Силы, Н ~ 85 ~ с, Н/см h, см найти № – – – – P M 8. Аналитическая динамика 8.1. Обобщенные координаты Число координат, определяющих положение механической системы, зависит от количества точек (или тел) входящих в систему, и от связей, наложенных на систему. Здесь рассматриваются системы с голономными связями, для которых число независимых координат, определяющих положение системы, совпадает с числом степеней свободы системы. Обобщенными координатами называют независимые между собой параметры любой размерности, которые однозначно определяют положение материальной системы. Пример. Для определения положения плоского маятника (рис. 31) можно использовать координату x (м), угол φ (рад), дугу M O M S м или площадь сектора OM O M м2 . Радиусы-векторы точек системы могут быть выражены через обобщенные координаты rk rk q1, q2 , , qs . Обобщенными скоростями q j называют производные обобщенных координат по времени: q j dq j / dt ( j 1, S ) . Размерность обобщенной скорости зависит от размерности соответствующей обобщенной координаты. Если q линейная величина, то q линейная скорость; если q угол, то q угловая скорость; если q площадь, то q секторная скорость и т. д. 8.2. Обобщенные силы Дадим системе виртуальное перемещение δq1,δq2 , ,δqs . Активные силы системы на этом перемещении совершат работу S δA Q1δq1 Q2δq2 QS δqS Q j δq j . j 1 Коэффициенты Q1, Q2 ,..., QS при приращениях обобщенных координат в выражении работы называются обобщенными силами. Способы вычисления обобщенных сил 1) Обобщённые силы можно вычислить по формулам ~ 86 ~ rk , i 1,2,3,..., S ; qi k 1 здесь rk (q1,..., qs ; t ) радиус-вектор k–той точки. 2) Дадим системе виртуальное перемещение так, чтобы положительное приращение δq1 получила первая обобщенная координата, при неизменных остальных обобщенных координатах. Работа δA1 активных сил системы δA δ A1 Q1 δq1, и Q1 1 . δq1 Остальные обобщенные силы определяются аналогичным способом. 3) Вместо виртуального перемещения можно рассматривать движение с виртуальными скоростями q j и виртуальную мощность активных сил. Обобщенными силами будут коэффициенты при обобщенных скоростях в выражении виртуальной мощности сил системы. 4) Если силы системы потенциальны, то обобщенные силы П , Qi qi где П потенциальная энергия системы. Размерность обобщенной силы Q j зависит от размерности обобn Qi Fk щенной координаты q j и определяется равенством [Q j ] [ A] / [q j ] , где [ A] размерность работы. Так, если обобщенная координата - линейная величина, то обобщенная сила имеет размерность силы; если обобщенная координата - угловая величина, то обобщенная сила имеет размерность момента; и т. д. Пример. Вычислить обобщенные силы двойного математического маятника, движущегося в вертикальной плоскости. Маятник состоит из шарнирно соединенных невесомых стержней OM1 и M1M 2 длиной l1 и l2 , на концах которых укреплены грузы массой m1 и m2 . Рассматриваемая система имеет две степени свободы. За обобщенные координаты принимаем углы φ1 и φ 2 (рис. 32). Учитывая, что силы системы являются потенциальными, применим четвертый способ вычисления обобщенных сил. Потенциальную ~ 87 ~ энергию системы вычислим как работу сил m1 g и m2 g при переходе системы из текущего положения в начальное, которое совпадает с вертикалью. При этом точка приложения силы m1 g опустится на h1 l1 l1 cosφ1 , а точка приложения силы m2 g на h2 h1 l2 (1 cosφ2 ) : m1gh1 m2 gh2 m1gl1 (1 cosφ1 ) m2 g[l1 (1 cosφ1 ) l2 (1 cosφ2 )] Тогда (m1 m2 ) gl1 sin φ1 ; φ1 Q2 m2 gl2 sin φ2 . φ2 Q1 8.3. Уравнения Лагранжа Процесс составления дифференциальных уравнений движения значительно упрощается при использовании уравнений Лагранжа. Преимущества этих уравнений определяются тем, что их вид и их число не зависит ни от количества точек или тел, входящих в механическую систему, ни от характера движения, а определяется лишь числом степеней свободы системы. Уравнения Лагранжа для механических систем с идеальными, удерживающими, голономными связями имеют вид d T T Qi , (i 1,2,3,..., S ) . dt qi qi Здесь q1,..., qS ; q1,..., qS обобщённые координаты и обобщённые скорости; S – число степеней свободы системы; T T (qi , qi , t ) кинетическая энергия; Qi обобщённые силы. Уравнения Лагранжа в случае потенциальных сил. Если все силы системы потенциальны, то обобщенные силы выражаются через потенциальную энергию системы как Q j / q j , а уравнения Лагранжа запишутся в виде d T T 0, ( j 1, S ) . dt q j q j q j Так как потенциальная энергия не зависит от обобщенных скоростей, то (T ) / q j T / q j . Введем в рассмотрение функцию Лагранжа: L T , ~ 88 ~ тогда уравнения Лагранжа запишутся так: d L L 0, ( j 1, S ) . dt q j q j Последовательность действий при составлении уравнений движения с помощью уравнений Лагранжа: 1) изобразить систему в текущем положении; 2) определить число степеней свободы; 3) выбрать обобщенные координаты, 4) записать в общем виде уравнения Лагранжа для каждой обобщенной координаты; 5) вычислить кинетическую энергию системы в абсолютном движении, выражая ее через обобщенные скорости и обобщенные координаты; 6) согласно уравнениям Лагранжа вычислить частные производные кинетической энергии; 7) изобразить активные силы системы и реакции неидеальных связей; 8) вычислить обобщенные силы по всем обобщенным координатам; 9) подставить частные производные кинетической энергии и обобщенные силы в уравнения Лагранжа, выполнить дифференцирование по времени. В результате получаем дифференциальные уравнения движения данной механической системы. Пример. Платформа 1 массы m1 8m скользит без трения по горизонтальной поверхности. По платформе катится без скольжения однородный цилиндр 2 массы m2 2m , ось которого соединена с платформой пружиной жесткости c (рис. 33). Составить дифференциальные уравнения движения системы. Изображаем систему в текущем положении (рис. 33). Система имеет две степени свободы. Выбираем в качестве обобщенных координат горизонтальное перемещение платформы S и удлинение пружины x . Когда пружина не деформирована, она имеет длину l0 . Таким образом, q1 S , q2 x . Активными силами являются силы тяжести m1 g и m2 g платформы и цилиндра и сила упругости пружины. Активные силы потенциальны, поэтому используем уравнения Лагранжа в виде: ~ 89 ~ d T T 0, ( j 1, S ) . dt q j q j q j (a) Кинетическая энергия системы T T1 T2 , где T1 кинетическая энергия платформы, T2 кинетическая энергия цилиндра. Так как платформа движется поступательно, а движение цилиндра плоское, то 1 1 1 2 (б) T mV m2VC2 J C ω2 , 1 1 2 2 2 где V1 и VC абсолютные скорости платформы и центра масс цилиндра, ω абсолютная угловая скорость цилиндра, J C m2 R 2 2 момент инерции цилиндра относительно оси вращения, проходящей через его центр масс перпендикулярно плоскости движения. Считаем, что платформа и цилиндр движутся в сторону увеличения обобщенных координат: V1 s, VC s x . P мгновенный центр скоростей цилиндра в его движении относительно платформы, R радиус цилиндра; ω x R . Подставляя в (б) значения скоростей и значения J C , m1 , m2 , получаем 1 2 T 4ms 2 m s x mx 2 . 2 Находим частные производные кинетической энергии по обобщенным скоростям и обобщенным координатам: T T T T 10ms 2mx; 3mx 2ms; 0; 0. s x S x Потенциальная энергия сил тяжести равна нулю. Потенциальная 1 энергия пружины П сx 2 . 2 П П 0; сx . Частные производные: s x Подставляем частные производные кинетической и потенциальной энергии в уравнения Лагранжа (a) d d (10ms 2mx) 0; 3mx 2ms сx 0 . dt dt Получаем дифференциальные уравнения движения системы: 5s x 0; 3mx cx 2ms 0. ~ 90 ~ Т Контрольные вопросы 1. Что называется числом степеней свободы системы? 2. Что представляют собой обобщённые координаты? 3. В каком соотношении находятся число степеней свободы голономной системы и число независимых обобщённых координат? 4. Что называется обобщённой силой? 5. От чего зависит размерность обобщённой силы? 6. От чего зависит число уравнений Лагранжа для данной механической системы? 7. Какой вид имеют уравнения Лагранжа? Таблица 18 Тестовые задания № Задание/ответ Схема Сумма элементарных работ активных сил имеет вид: δAk 5δq1 8δq2 20δq3 . Обобщённая сила, соответст1 вующая обобщённой координате q3 , равна … 2 Ответ: 20 В потенциальном силовом поле для механической системы с потенциальной энергией П 7 x Дж , обобщенная сила Qx ... Н . Ответ: 7 3 Обобщенной координате S (м) соответствует обобщенная сила Qx ... Н . Ответ: 10 4 Для механической системы с кинетической энергией T 3φ2 Дж , обобщенной силой Q 27φ Н м дифференциальное уравнение движения … Ответ: 2φ 9φ 0 5 Для механической системы с кинетической энергией T 8φ2 Дж , потенциальной энергией П 4φ2 Дж , дифференциальное уравнение движения … Ответ: 2φ φ 0 ~ 91 ~ окончание табл. 18 6 7 8 Механическая система с кинетической энергией 2 2 T 0,5x y xy Дж , обобщенными силами Qx 3 Н и Qy 2 Н движется с ускорением y ... м/с2 . Ответ: 5 При движении системы с обобщенными силами Qy 10 H , Qz 20 H и кинетической энергией Т y 2 2 z 2 Дж , отноy шение ускорений ... z Ответ: 1 Кинетическая энергия системы T 5φ2 Дж . Обобщённая сила Qφ 20 Н м . Ускорение груза a ... м/с2 . Ответ: 6 Индивидуальное задание №6 Применение уравнений Лагранжа к исследованию движения механической системы с двумя степенями свободы Механическая система (таблица 19) движется под воздействием постоянных сил и пар сил. Составить дифференциальные уравнения движения системы в обобщённых координатах. Необходимые данные приведены в таблице 20. Там же указаны обобщенные координаты, которые следует использовать при выполнении задания. Считать, что качение колёс происходит без проскальзывания. Колёса, для которых в таблице радиусы инерции не указаны, считать сплошными однородными дисками. Кривошипы рассматривать как тонкие однородные стержни. Принять, что в вариантах 6, 9, 11, 20, 22 и 30 механизм расположен в горизонтальной плоскости. Примечания: Радиусы инерции тел 2 и 3 определены относительно центральной оси, перпендикулярной плоскости чертежа. При выполне- ~ 92 ~ нии варианта 5 следует иметь в виду, что блоки 5 и 6 насажены на общую ось свободно, их массы одинаковы. Пример выполнения задания. Дано: Массы тел механической системы (рис. 34): m1 3m ; m2 8m; m4 m6 2m; m3 4m ; M 3mgr постоянный момент; b mη коэффициент пропорциональности в выражении силы R bV3 сопротивления движению тела 3 ( V3 скорость тела 3); r – радиус однородных дисков 4, 6 и 2. Составить дифференциальные уравнения движения системы в обобщённых координатах q1 x1, q2 x2 . На рис. 34 система изображена в движении. Решение. Для решения задачи применим уравнения Лагранжа II рода: d T T Q1 ; dt x1 x1 d T T Q2 . dt x2 x2 (1) (2) Здесь T кинетическая энергия системы; Q1 и Q2 обобщённые силы. Для данной системы T Ti Выразим абсолютные скорости центров масс твёрдых тел системы через обобщённые скорости: V1 V3 x1 , V2 x1 x2 . Здесь учтено, что для тела 2 x1 переносная скорость при движении вместе с нитью, x2 относительная скорость. Угловые скорости тел (рис. 34) ~ 93 ~ x1 ; r x2 ω2 . r ω 4 ω6 Моменты инерции блоков относительно центральных осей: 2mr 2 J4 J6 mr 2 . 2 Момент инерции цилиндра 2 относительно центральной оси: 8mr 2 J2 4mr 2 . 2 Кинетическая энергия тел: T1 2 mV 3 1 1 m x12 . 2 2 J 4 ω24 mx12 m2V22 J 2 ω 22 2 2 ; T2 4m x1 x2 2mx2 ; T4 2 2 2 2 Получим: m3V32 J 6 ω62 1 2 2 T3 2mx1 ; T6 mx1 . 2 2 2 2 9 (3) T mx12 2 mx22 4 m x1 x2 . 2 Для вычисления обобщённой силы Q1 зададим системе виртуальное движение x1 0; x2 0 и подсчитаем мощность сил N1 m1g x1 R x1 M ω6 m2 g x1, или M M N1 3mg bx1 8mg x1 5mg bx1 x1 . r r Обобщённая сила Q1 равна коэффициенту при x1 в выражении мощности N1 : M Q1 5mg bx1 . (4) r Для вычисления обобщённой силы Q2 зададим системе виртуальное движение x1 0; x2 0 и подсчитаем мощность сил N2 m2 g x2 8mg x2 . ~ 94 ~ Обобщённая сила Q2 равна коэффициенту при x2 в выражении мощности N 2 : (5) Q2 8mg . Найдем значения слагаемых уравнений Лагранжа T (6) 9mx1 8m x1 x2 17mx1 8mx2 ; x1 T (7) 4mx2 8m x1 x2 12mx2 8mx1 ; x2 T T 0; 0; (8) x1 x2 d T 17mx1 8mx2 dt x1 (9) d T (10) 12mx2 8mx1 dt x2 Подставляя в (1) и (2) выражения (4), (5), (8 – 10) и значения М и b, получим дифференциальные уравнения движения системы: 17 x1 8 x2 x1 8 g , . 2 x1 3x2 2 g. ~ 95 ~ Таблица 19 Схемы механизмов к заданиям №6 задание №1 задание №2 задание №3 задание №4 задание №5 задание №6 ~ 96 ~ продолжение табл. 19 задание №7 задание №8 задание №9 задание №10 задание №11 задание №12 ~ 97 ~ продолжение табл. 19 задание №13 задание №14 задание №15 задание №16 задание №17 задание №18 ~ 98 ~ продолжение табл. 19 задание №19 задание №20 задание №21 задание №22 задание №23 задание №24 ~ 99 ~ окончание табл. 19 задание №25 задание №26 задание №27 задание №28 задание №29 задание №30 ~ 100 ~ Таблица 20 № варианта № задания Данные для индивидуального задания №6 m1 1 1 2m 6m m m - - - - - q1 ; q3 2 2 m 3m - - - - - M - q1 ; q3 3 3 m 3m 2m - - r 2 - M4 - q1 ; q4 4 4 m 2m 2m 2m - - - f q1 ; q3 5 6 7 8 9 10 11 5 6 7 8 9 10 11 m m 3m m m 2m 2m 4m 3m m 2m 2m m - 2m 2m 2m 2m 2m 2m 2m 3m m 3m 2m m - - m m r 2 2r 4r f f f - q1 ; q2 q1 ; q2 q1 ; q2 q1 ; q2 q1 ; q2 q1 ; q2 q1 ; q3 12 13 14 12 13 14 2m m - 2m 2m 2m - - P - 2m 5m 3m m r 2 - M1 , M 2 P1 ; P2 M1 , M 2 M1 , M 2 M f - q1 ; q2 q1 ; q2 q1 ; q3 15 15 3m m - - - - P; M - q1 ; q3 16 16 2m 3m - q 2 ; q3 17 17 m - q1 ; q3 18 18 19 массы тел m радиус инерции нагрузка m2 m3 m4 m5 ρ2 ρ3 P, M 3m m f qi m - 2r - 3m 2m 2m 2m 2m - - 2m 2m m m 3m r 2 - M - - M4 f q1 ; q2 19 2m 2m 3m m - - - f q1 ; q2 20 21 20 21 2m 2m 3m m 3m 3m m - r 2 - ρ5 1,5r M1 , M 2 - - q1 ; q2 q1 ; q2 22 23 24 22 23 24 m 3m - 2r - M1 , M 2 - q1 ; q2 q1 ; q2 M f - q2 ; q4 25 26 27 r - P1 ; P2 M M f - q1 ; q2 q1 ; q2 q1 ; q2 28 29 30 - P P M1 , M 2 f - q1 ; q2 q1 ; q2 q1 ; q2 2m 2m m 3m m 3m 25 26 27 2m 2m m m 3m 2m 2m 2m 3m 28 29 30 m 2m 3m 4m m m 3m 2m 2m 2m m m 2m m m 2m 3m m - - 2m m - - r 2 - ~ 101 ~ № варианта № задания продолжение табл. 20 31 32 33 1 2 3 2m m m 6m 3m 3m 34 4 m 2m 2m 2m - 35 5 m 4m 2m 2m 36 6 m 2m 2m r 2 - 3m - - 2r - M1 , M 2 - q1 ; q3 37 7 3m 3m m m - - - P1 ; P2 - q1 ; q5 38 8 m 2m 2m 2m - - - f q3 ; q4 39 9 m 3m - - - - M1 , M 2 - q2 ;q3 40 10 2m 2m 2m 2m m - m - - - f q3 ; q4 41 11 m 3m 2m m - 4r M1 , M 2 - q1 ; q2 42 12 2m 5m m - - - r 2 - P f q1 ; q3 43 13 m 3m 2m - - - - - q3 ; q4 44 14 2m m m 2m 2m - - - - q2 ;q3 45 46 15 16 3m 2m m 3m m - 2r - q2 ; q4 q1 ; q3 17 m 3m 2m - - - q2 ; q4 48 18 2m 2m m m 3m r 2 - M - - 47 2m 2m 2m M P; M - M4 f q3 ; q4 49 19 2m 2m 3m m - - - f q3 ; q4 50 20 3m m 3m - - M1 , M 2 - q2 ;q3 51 21 2m 2m r 2 - 2m 3m 2m m - ρ5 1,5r - - q3 ; q4 52 22 m 3m 2m m - - - M1 , M 2 - q2 ;q3 53 23 2m m m m 3m - - - f q2 ;q3 54 24 m 3m m 2m - 2r - M - q1 ; q3 55 56 25 26 2m 2m m m 3m 2m 3m - - P1 ; P2 M f - q1 ; q4 q3 ; q4 57 27 2m 2m 3m m 2m M - q3 ; q4 58 28 m 3m m - - r 2 - r - P - q3 ; q4 59 29 2m 4m m m - - - P f q2 ;q3 60 30 3m 2m 2m - - - - M1 , M 2 - q1 ; q3 массы тел радиус инерции нагрузка f qi q2 ; q4 q2 ; q4 q2 ;q3 m1 m2 m3 m4 m5 ρ2 ρ3 P, M m - - - - - 2m m - M M4 - - - f q2 ; q4 - - f q2 ;q3 r 2 ~ 102 ~ окончание табл. 20 № варианта № задания радиус инерции m1 61 1 2m 6m m m - - - - - q3 ; q4 62 2 m 3m - - - - - M - q2 ;q3 63 3 m 3m 2m - - r 2 - M4 - q2 ; q4 64 4 m 2m 2m 2m - - - f q1 ; q4 65 5 m 4m 2m 2m - - f q5 ; q6 66 6 m 2m 2m r 2 - 3m - - 2r - M1 , M 2 - q2 ;q3 67 7 3m 3m m m - - - P1 ; P2 - q3 ; q4 68 8 m 2m 2m 2m - - - f q1 ; q3 69 9 m 3m - - - - M1 , M 2 - q1 ; q3 70 10 2m 2m 2m 2m m - m - - - f q2 ;q3 71 11 m 3m 2m m - 4r M1 , M 2 - q2 ;q3 72 12 2m 4m m m - - r 2 - P f q1 ; q3 73 13 m 3m 2m - - - - - q1 ; q3 74 75 14 15 2m m m m 2m 2m - - - M P; M - q1 ; q4 q2 ;q3 76 77 16 17 2m 2r m 3m 3m - M - - q2 ; q4 q1 ; q4 78 18 M4 f q1 ; q3 19 2m 2m - 79 2m 2m - f q2 ; q4 80 20 M1 , M 2 - q1 ; q3 81 21 2m 2m r 2 - 82 22 83 массы тел 3m нагрузка m2 m3 m4 m5 ρ2 ρ3 P, M - 2m 2m 2m 2m - m m 3m r 2 - 3m m - - 3m m 3m - - 2m 3m 2m m - m 3m 2m m - 23 2m m m m 84 85 24 25 m 3m 2m 2m 2m m m 86 26 m 3m 87 27 2m 88 28 m m f qi - - q2 ; q4 - r 2 - M1 , M 2 - q1 ; q3 3m - - - f q3 ; q4 - - 2r - - M P1 ; P2 f q1 ; q4 q2 ;q3 2m 3m - - r M - q2 ;q3 2m 3m m 2m - M - q1 ; q3 3m m - - r 2 - - P - q2 ; q4 ~ 103 ~ 9. Удар 9.1. Основные положения теории удара Явление, при котором скорости точек тела за очень малый промежуток времени изменяются на конечную величину, называется ударом. Силы, возникающие при ударе, будем называть ударными силами. Время удара обозначим через τ . Действие ударной силы оценивают ударным импульсом τ S уд Fуд dt 0 Ударный импульс – конечная величина. Обозначения: V скорость точки до удара, V cкорость точки после удара. Применим к явлению удара теорему об изменении количества движения: m V V S Изменение количества движения материальной точки за время удара равно действующему на точку ударному импульсу. Это – основное уравнение теории удара. Основные положения теории удара: 1.Удар происходит мгновенно. 2.Тело при ударе не изменяет своего положения. 3.Действие неударных сил (таких, как сила тяжести) можно не учитывать. 4.Изменения скоростей точек тела за время удара определяются основным уравнением теории удара. 9.2. Коэффициент восстановления (гипотеза Ньютона) Коэффициент восстановления равен отношению модуля нормальной составляющей относительной скорости точек контакта тел после удара к его значению до удара VAn VBn , k n VA VBn где A, B точки контакта (см. рис. 35). Относительные скорости точек контакта: VA VB скорость сближения перед ударом; ~ 104 ~ VA VB скорость разлета после удара. Коэффициент восстановления учитывает физические свойства тел. Определяется экспериментально. При прямом ударе тела о неподвижную преграду коэффициент восстановления равен отношению модуля скорости тела в конце удара к модулю скорости в начале удара: k V V . Предельные случаи: – абсолютно упругий удар ( k 1 ); – абсолютно неупругий удар ( k 0 ). В первом случае ( k 1 ) кинетическая энергия после удара полностью восстанавливается, во втором ( k 0 ) вся кинетическая энергия теряется на нагревание, деформацию и прочее. 9.3. Теорема об изменении количества движения механической системы при ударе Изменение количества движения системы за время удара равно сумме всех внешних ударных импульсов, действующих на систему Q Q Ske . В проекциях на любую координатную ось x Qx Qx Skxe . Импульсы обычных сил при ударе не учитывают. Следствия: 1.Если геометрическая сумма всех внешних ударных импульсов равна нулю, то количество движения системы за время удара не изменяется. 2.Внутренние ударные импульсы не могут изменить количества движения системы. ~ 105 ~ 9.4. Теорема об изменении кинетического момента механической системы при ударе (теорема моментов) Изменение за время удара кинетического момента системы относительно какого-нибудь центра равно сумме моментов относительно того же центра всех действующих на систему внешних ударных импульсов. KO KO M O Ske . В проекциях на любую ось x K x K x M x Ske . Следствия: 1.Если сумма моментов внешних ударных импульсов относительно какого-нибудь центра (или оси) равна нулю, то кинетический момент системы относительно этого центра (или оси) за время удара не изменяется. 2.Внутренние ударные импульсы не могут изменить кинетический момент системы. Пример. Однородный куб A с ребром b 1 м скользит без начальной скорости по гладкой опорной плоскости, наклоненной под углом α 30 к горизонту (рис. 37), и проходит расстояние b до соударения с упором B . Считая удар куба об упор абсолютно неупругим, определить угловую скорость ω вращения куба сразу после удара. Решение. Определим линейную скорость V куба перед ударом об упор. Используем для этого теорему об изменении кинетической энергии: T T0 Ak . (а) Движение началось из состояния покоя, поэтому T0 0 . Кинетиче1 ская энергия перед ударом об упор T mV2 . 2 Работу совершает только сила тяжести: Ak mgb sin α . Подставляя все эти значения в уравнение (а), найдем: ~ 106 ~ откуда 1 mV2 mgb sin α , 2 V 2 gb sin α . В момент удара (рис. 38) на куб в точке B действует ударный импульс S уд . После удара куб приобретает угловую скорость ω вращения вокруг оси Bz , перпендикулярной плоскости чертежа. Момент ударного импульса M Bz S уд 0 , следовательно, кинетический момент относительно оси Bz за время удара не изменяется: (б) K Bz K Bz . Кинетический момент куба относительно оси Bz перед ударом: b K Bz mV . 2 Кинетический момент куба относительно оси Bz после удара: 2 K Bz J Bz ω , где J Bz mb 2 . 3 Подставляя эти значения и значение V в уравнение (б), найдем ω Окончательно ω 2,35 3 2g sin α . 4 b рад . с Контрольные вопросы 1. Какое явление называется ударом? 2. Что служит мерой взаимодействия тел при ударе? 3. Что называется ударным импульсом? 4. Как следует поступать с неударными силами при рассмотрении удара? 5. Запишите основное уравнение теории удара для материальной точки. 6. Сформулируйте теорему об изменении количества движения системы при ударе. 7. Сформулируйте теорему об изменении кинетического момента системы при ударе. 8. Могут ли внутренние ударные импульсы изменить кинетический момент системы? ~ 107 ~ 9. Верно ли, что за время удара тело не меняет своего положения? 10. Что называется коэффициентом восстановления при ударе? 11. В каких пределах может изменяться коэффициент восстановления? Таблица 21 № 1 2 3 4 5 Тестовые задания Задание/ответ Схема На материальную точку массой 0,6 кг, движущуюся со скоростью V 3i 2 j м/с , подействовал ударный импульс S (1,8 i 2,4 j ) Н с . После удара модуль скорости V ... м/с . Ответ: 6 Однородный стержень массой 4 кг двигался поступательно со скоростью V 2 м/с . После приложения ударного импульса S 16 Н с скорость VC ...м/с . Ответ: 2 Однородный стержень массой 4 кг двигался поступательно. После приложения ударного импульса угловая скорость S 1,6 Н с ω ...рад/с . Ответ: 2 После удара об упор угловая скорость ω 3,5рад/с ; коэффициент восстановления k 0,7 . Угловая скорость перед ударом ω ...рад/с . Ответ: 5 После абсолютно неупругого удара тел с массами m1 3 кг , m2 1кг их общая скорость V ...м/с . Ответ: 9 ~ 108 ~ 10. Колебания 10.1. Устойчивость положения равновесия Равновесие системы в данном положении называется устойчивым, если, выведенная из этого положения малым возмущением, во все последующее время она движется в малой окрестности положения равновесия или возвращается к нему. Пример. На рисунке в варианте «а» равновесие маятника в нижнем вертикальном положении устойчиво; в варианте «б» равновесие маятника в верхнем вертикальном положении неустойчиво (рис. 39). Теорема Лагранжа – Дирихле: если потенциальная энергия консервативной системы с идеальными стационарными связями имеет в положении равновесия строгий минимум, то равновесие системы в этом положении является устойчивым. Это условие – достаточное. Для консервативной системы с одной степенью свободы достаточные условия устойчивости положения равновесия имеют вид: 2П П 0, 2 0. q 0 q 0 Пример. Механическая система состоит из обращенного математического маятника массой m и длиной l и спиральной пружины с коэффициентом жесткости С (рис 40). При каких значениях параметров верхнее положение равновесия маятника будет устойчивым? Решение. Для рассматриваемой системы потенциальная энергия: 1 П Cφ2 mgl 1 cosφ ; 2 считая φ малым, найдем значение П φ с точностью до φ 2 : φ2 φ4 1 cosφ ... 2! 4! φ2 П φ C mgl . 2 ~ 109 ~ П П C mgl φ. При φ 0 0. φ φ 0 Первое условие устойчивости положения равновесия выполняется. 2П 2П Находим Условие C mgl . 2 0 выполняется, если φ 2 φ 0 Находим C mgl . Вывод: верхнее положение равновесия маятника устойчиво при условии, что его параметры удовлетворяют неравенству C mgl . 10.2. Свободные линейные колебания материальной точки Точка M движется прямолинейно под действием восстанавливающей силы F , пропорциональной расстоянию до неподвижного центра O и направленной к этому центру (рис. 41). Проекция силы F на ось Ox : Fx C x . Применим основной закон динамики и составим дифференциальное уравнение движения материальной точки вдоль оси Ox : m x Cx . С Делим обе части уравнения на m , вводим обозначение k 2 . m Уравнение примет вид: x k 2x 0 . (1) Это дифференциальное уравнение свободных линейных колебаний при отсутствии сопротивления. Линейными колебания (и совершающая их механическая система) называются потому, что определяющее их дифференциальное уравнение (1) является линейным. Общее решение уравнения (1) x Asin kt α . (2) Скорость точки Vx x Ak cos kt α . (3) Колебания, совершаемые точкой по закону синуса, называются гармоническими колебаниями. Наибольшее отклонение А точки М от центра колебаний О называется амплитудой колебаний. Величина φ kt α называется фазой колебаний. Величина α называется начальной фазой колебаний. Величина k называется круговой частотой ~ 110 ~ колебаний. Промежуток времени T , в течение которого точка совершает одно полное колебание, называется периодом колебаний. Период 2π T . k Величина ν , обратная периоду и определяющая число колебаний за одну секунду, называется частотой колебаний: 1 ν . T Определение амплитуды и начальной фазы колебаний по начальным условиям. Положим, что при t 0 x x0 и Vx V0 ; из (2) и (3) получим V x0 A sin α, 0 A cosα . k Сложив почленно квадраты этих равенств, найдем V02 A x 2 . k Разделив почленно одно уравнение на другое, получим kx tgα 0 . V0 Рассмотренные здесь колебания называют линейными, так как они описываются линейным дифференциальным уравнением. Свободные линейные колебания обладают следующими свойствами: – амплитуда и начальная фаза колебаний зависят от начальных условий; – частота k и период T колебаний не зависят от начальных условий и являются неизменными характеристиками данной системы. 2 0 10.3. Влияние постоянной силы на свободные линейные колебания Пусть на материальную точку действует восстанавливающая сила F F C OM и постоянная по модулю и направлению сила P (рис. 42). Введем в рассмотрение статическое отP клонение λ ст . C В рассматриваемом случае положением равновесия точки M будет точка O1 , отстоящая от O на λ ст . Примем положение равновесия O1 за начало координат. Тогда Fx C ( x λст ), Px P . ~ 111 ~ Дифференциальное уравнение движения m x C x λст P или, C поскольку P C λст , k 2 : m x k 2x 0 . Это уравнение совпадает с полученным ранее дифференциальным уравнением свободных колебаний материальной точки под действием только восстанавливающей силы F . Следовательно, постоянная сила P не изменяет характер колебаний, а лишь смещает центр колебаний в сторону действия силы на величину статического отклонения λ ст . Пример. Определить период малых свободных колебаний однородного диска массой 2 кг (рис. 43); коэффициенты жесткости пружин C1 900 Н/м , C2 700 Н/м . Решение. Для составления дифференциального уравнения движения используем теорему об изменении кинетического момента механической системы: dK z M ze . dt Обозначим через φ угол поворота диска. Кинетический момент 2 mR момент инерции диска. Удлинение нижней K z Jω Jφ , где J 2 пружины равно сжатию (укорочению) верхней и равно R φ . Сумма моментов внешних сил относительно оси вращения диска М ze C1 Rφ R C2 Rφ R C1 C2 R2φ . Подстановка значений K z и M ze в уравнение теоремы приводит к дифференциальному уравнению φ k 2φ=0 , 2 C1 C2 круговая частота свободных колебаний. m Тогда период колебаний: 2π π T с. k 20 где k ~ 112 ~ 10.4. Свободные колебания при вязком сопротивлении (затухающие свободные колебания) Добавим к восстанавливающей силе F силу вязкого трения, то есть силу, пропорциональную первой степени скорости: R μV (рис. 44). Имеем: Fx Cx, Rx μVx μx . Дифференциальное уравнение движения mx Cx μx . Разделим уравнение C μ k 2 , 2b . Назовем b коэффициенна m и введем обозначения: m m том затухания. Получим дифференциальное уравнение свободных колебаний при вязком сопротивлении (1) x 2bx k 2 x 0 . Коэффициенты b и k имеют одинаковую размерность, следовательно, их можно сравнивать по величине. Решение дифференциального уравнения ищут в виде x e pt . Подстановка решения в дифференциальное уравнение приводит к характеристическому уравнению p 2 2bp k 2 0 ; его корни p1,2 b b2 k 2 . В зависимости от соотношения величин b и k корни могут быть вещественными или комплексными. Рассмотрим случай, когда b k , то есть когда сила вязкого тре- ния мала. Введем обозначение k1 k 2 b2 , тогда p1,2 b ik1 , то есть корни в этом случае комплексные. Общее решение уравнения (1) x Aebt sin k1t α . (2) Величины A и α являются постоянными интегрирования и определяются по начальным условиям. График колебаний представлен на рисунке 45. Колебания по закону (2) называются затухающими. Это движение не является периодическим; тем не менее промежуток времени T1 , равный периоду функции sin k1t α , принято называть периодом затухающих колебаний. Период 2π 2π T . 2 2 k1 k b При затухающих колебаниях размахи колебаний (максимальные отклонения в одну сторону) убывают по закону геометрической про- ~ 113 ~ грессии. Знаменатель этой прогрессии Aebt называется декрементом колебаний. Модуль его логарифма bT1 называется логарифмическим декрементом. Случай, когда b k (большое сопротивление). В этом случае оба корня характеристического уравнения – числа действительные и отрицательные. Общее решение имеет вид: x C1e a1t C2e a2t . Функция вида e at , где a 0 , монотонно убывает. Движение в этом случае не будет колебательным. Пример. Тело массой m 20,4 кг установлено на двух пружинах жесткостью С1 4 Н/м , С2 6 Н/м . Тело отведено из положения равновесия вверх на 4 см и отпущено без начальной скорости (рис. 46). Найти закон движения, учитывая силу сопротивления среды с R μV , μ 2 Н . см Решение. Поместим начало отсчета координаты x в положение статического равновесия тела. Дифференциальное уравнение движения mx C1x C2 x μx или x 2bx k 2 x 0 , μ C C2 рад ; b 4,9 c1, k 7 где 2b , k 2 1 m m с Общее решение дифференциального уравнения имеет вид x Aebt sin k1t α , k1 k 2 b2 , k1 5 рад/с; ~ 114 ~ x Aebt cos k1t α Abebt sin k1t α . Полагая в общем решении t 0 и используя начальные условия, получим: 0,04 A sin α, 0 5 A cosα 4,9 A sin α. 5 1,02 1, α 45 . Найдем из второго уравнения tgα 4,9 0,04 0,057 м . Из первого уравнения A sin 45 4,9t Закон движения тела x 0,057e sin 5t π / 4 . 10.5 Вынужденные колебания в линейной системе без сопротивления при гармонической возмущающей силе Рассмотрим случай, когда на материальную точку действуют две силы: восстанавливающая сила F и возмущающая сила Q . Пусть возмущающая сила является гармонической, то есть ее проекция на ось Ox : Qx Q0 sin t . Колебания, возникающие под действием этой силы, называются вынужденными. Дифференциальное уравнение движения имеет вид Q x kx 0 sin t (1) m Исключив случай равенства частот k , частное решение уравнения (1) будем искать в виде (2) x B sin t . Подстановка частного решения (2) в уравнение (1) приводит к уравнению Q B2 Bk 2 0 m откуда находим Q /m B 20 2 . k Введем в рассмотрение статическое отклонение xст Q0 / C . ~ 115 ~ Q0 C xст k 2 C m Тогда B 2 или B k 2 k 2 2 xст . 2 1 2 k Общее решение дифференциального уравнения (1) будет суммой общего решения соответствующего однородного дифференциального уравнения и частного решения (2) Q /m x С1 cos kt C2 sin kt 2 0 2 sin t . (3) k Скорость Q /m x С1k sin kt C2k cos kt 2 0 2 cos t . (4) k Зададим начальные условия: при t 0, x x0 , x x0 . В (3),(4) положим t 0 , получим: Q /m x0 C1; x0 C2k 2 0 2 , k откуда x Q /m C2 0 2 0 2 . k k k Заданным начальным условиям соответствует решение x Q /m Q /m x x0 cos kt 0 sin kt 2 0 2 sin kt 2 0 2 sin t (5) k k k k Практически реализовать механическую колебательную систему без сопротивления невозможно. В реальных системах всегда присутствуют силы сопротивления, вследствие чего колебания с собственной частотой k затухают. Поэтому в рассматриваемом движении основное значение имеют вынужденные колебания с частотой возмущающей силы по закону xст x sin t . 1 2 / k 2 1 Безразмерный коэффициент η называется коэффици1 2 / k 2 ентом динамичности. Он показывает, во сколько раз амплитуда установившихся вынужденных колебаний больше статического отклонения. Резонанс. В решении (5) положим x0 0, x0 0 . Пусть частота возмущающей силы приближается к собственной частоте системы: k. ~ 116 ~ В формуле (5) / k 1, k 2 2 k k 2 k и Q0 / m x sin t sin kt 2 k На основании известной формулы αβ α β sin α sinβ 2cos sin 2 2 найдем: k sin t sin kt 2cos t sin t. 2 C учетом этого формулу для x можно представить в виде k Q0 sin 2 t x t cos t . 2m k t 2 Из курса высшей математики известно, что функция, заключенная в квадратные скобки, при k стремится к единице. Тогда Q x 0 t cos t . 2m На рисунке 48 показан график этой функции. Видно, что при k амплитуда колебаний неограниченно возрастает, причем амплитуда растет пропорционально времени. Это явление называется резонансом. 10.6. Вынужденные колебания при вязком сопротивлении Рассмотрим движение материальной точки вдоль оси x под действием линейной восстанавливающей силы F , силы вязкого трения R и возмущающей силы Q. Имеем: Fx Cx, Rx μx, Qx Q0 sin t . Дифференциальное уравнение движения ~ 117 ~ mx Cx μx Q0 sin t . Разделим уравнение на m и введем обозначения: C μ k 2 , 2b . m m Получим Q0 sin t . (1) m Рассмотрим только установившиеся вынужденные колебания x B sin t β . Введем обозначение φ t β . Тогда sin t sin φ β sin φ cosβ cosφ sinβ . Подставим этот результат, а также значения x и его первой и второй производных в уравнение (1): Q B2 sin φ 2bB cosφ k 2 B sin φ 0 sin φ cosβ cosφ sinβ . m Чтобы это уравнение выполнялось при любом φ (т.е. при любом t ), должны быть равны друг другу коэффициенты при sin φ и cosφ в левой и правой частях уравнения: Q Q B k 2 - 2 0 cosβ, 2bB 0 sinβ . m m Из полученных уравнений находим Q0 / m B ; 2 2 2 2 2 k - 4b x 2bx k 2 x 2b . k 2 - 2 Q Q C C Q Учтем, что 0 0 , k 2 , 0 xст смещение, вызываемое m C m m C статически приложенной постоянной силой Q0 . Тогда xст . B 2 2 2 2 b 1 k 2 4 k 4 tgβ Определяемая этой формулой зависимость амплитуды вынужденных колебаний от частоты возмущающей силы называется амплитудночастотной характеристикой колебательной системы. Отношение B / xст называют коэффициентом динамичности ~ 118 ~ 1 K 2 . b 1 k 2 4 k 4 Видно, что ни при каких значениях частоты возмущающей силы коэффициент динамичности не обращается в бесконечность. Если частота возмущающей силы близка к собственной частоте k , то амплитуда вынужденных колебаний достигает максимума. Это явление называется резонансом. Свойства вынужденных колебаний: – амплитуда вынужденных колебаний не зависит от начальных условий; – вынужденные колебания при наличии сопротивления не затухают; – частота вынужденных колебаний равна частоте возмущающей силы и не зависит от характеристик системы; –при малой возмущающей силе ( Q0 мало) можно получить интенсивные вынужденные колебания, если сопротивление мало, а частота близка к k (резонанс); – при большой возмущающей силе вынужденные колебания можно сделать малыми, если частота будет много больше k . Пример 1. Движение механической системы определяется дифференциальным уравнением q 4q 9q 10sin3t . Во сколько раз уменьшится амплитуда установившихся вынужденных колебаний при увеличении коэффициента сопротивления в 2 раза? Решение. Стандартный вид уравнения установившихся вынужденных колебаний Q q 2bq k 2 q 0 sin t . m Сравнивая уравнения, находим: b 2, k 2 9, Q0 / m 10, 3 . Амплитуда Q0 / m B . 2 2 2 2 2 k - 4b 2 2 2 Подставим в формулу численные значения k , , Q0 / m , найдем 1 B . Видим, что величины B и b обратно пропорциональны. Сле0,6b довательно, при увеличении коэффициента сопротивления в 2 раза амплитуда вынужденных колебаний уменьшится также в 2 раза. ~ 119 ~ Пример 2. Дифференциальное уравнение колебаний механической системы 64q 170q 3000q 150sin8t . Определить амплитуду установившихся вынужденных колебаний. Решение. Делим уравнение на 64 и сравниваем со стандартным: q 2,66q 46,9q 2,34sin3t . Сравнивая уравнения, находим: b 1,33; k 2 46,9; Q0 / m 2,34; 8. Q0 / m По формуле B находим B 0,086 м . 2 2 2 2 2 k - 4b 10.7. Малые свободные колебания системы с двумя степенями свободы Пусть положение системы определяется обобщенными координатами q1 , q2 и при q1 q2 0 система находится в устойчивом равновесии. Тогда для консервативной системы с голономными стационарными связями с точностью до квадратов малых величин 1 T a11q12 2a12q1q2 a22q22 ; 2 1 П c11q12 2c12 q1q2 c22 q22 . 2 Подставим T и П в уравнения Лагранжа: d T T П 0, i 1,2 . dt qi qi qi Имеем T П T 0, с11q1 c12 q2 , a11q1 a12 q2 , q1 q1 q1 d T a11q1 a12 q2 , dt q1 T П T d T 0; 0; a12 q1 a22 q2 ; a12 q1 a22 q2 . q2 q2 q2 dt q2 Получим дифференциальные уравнения малых колебаний системы с двумя степенями свободы a11q1 a12 q2 c11q1 c12q2 0, (1) a12 q1 a22 q2 c12 q1 c22 q2 0. ~ 120 ~ Таким образом, малые колебания консервативной системы с двумя степенями свободы около положения устойчивого равновесия описываются системой двух линейных однородных дифференциальных уравнений второго порядка с постоянными коэффициентами. Решение уравнений (1) будем искать в форме (2) q1 Asin kt α , q2 B sin kt α . Здесь A, B, k , α неизвестные постоянные. Продифференцируем выражения для q1 , q2 дважды по времени t : q1 Ak 2 sin kt α , q2 Bk 2 sin kt α . Подставим значения q1, q2 , q1, q2 в дифференциальные уравнения (1) и сократим на общий множитель sin kt α . Получим c c a 11 k 2 A c12 a12k 2 B 0, (3) 2 2 12 a 12 k A c22 a22 k B 0. Чтобы уравнения (3) давали для A и B решения, отличные от нуля, определитель системы должен быть равен нулю или, иначе, коэффициенты при A и B должны быть пропорциональны. Условие пропорциональности коэффициентов: c a 11 k 2 c12 a12k 2 B 11 n. (4) c12 a 12 k 2 c22 a22k 2 A Определитель системы должен быть равен нулю c11 a 11 k 2 c12 a12 k 2 0. 2 2 c12 a 12 k c22 a22k Раскрыв определитель, получим уравнение частот, или вековое уравнение: 11 c 11 a 11 k 2 c22 a22k 2 c12 a 12 k 2 0 . 2 (5) Корни этого уравнения k12 и k22 вещественны и положительны. Каждому положительному корню k1 и k2 соответствует одно частное решение (2), причем каждой частоте присущи свои значения A, B, α . Полагая в уравнении (4) сначала k k1 , затем k k2 , получим два значения n1 , n2 . Соответственно найдем B1 n1 A1, B2 n2 A2 . Итак, имеем два линейно независимых частных решения: 1 1 q1 A1 sin k1t α1 , q2 B1 sin k1t α1 (6) и 2 2 q1 A2 sin k2t α2 , q2 B2 sin k2t α2 (7) ~ 121 ~ Колебания, определяемые уравнениями (6) и (7), называются главными колебаниями, а их частоты k1 и k2 собственными частотами системы. В качестве частоты k1 всегда выбирается меньшая из двух собственных частот. Колебание с частотой k1 называют первым главным колебанием, а с частотой k2 вторым главным колебанием. Числа n1 , n2 , определяющие отношения амплитуд в каждом из этих колебаний, называют коэффициентами формы. Общее решение системы дифференциальных уравнений (1) будет линейной комбинацией частных решений (6) и (7): q1 A1 sin k1t α1 A2 sin k2t α 2 , (8) q2 n1 A1 sin k1t α1 n2 A2 sin k2t α 2 . Произвольные постоянные A1, A2 , α1, α2 определяются по начальным условиям. Собственные частоты k1 , k2 и коэффициенты формы n1 , n2 не зависят от начальных условий и являются основными характеристиками колебательной системы. Обе координаты в каждом главном колебании изменяются по гармоническому закону, имея одинаковые частоты и фазы. Обе координаты одновременно обращаются в нуль, одновременно достигают максимальных значений. Пример. Определить собственные частоты и коэффициенты формы малых колебаний двойного физического маятника, образованного однородными стержнями 1 и 2 одинаковой массы m и длины l (рис. 50). Решение. Примем за обобщенные координаты углы φ1 , φ2 . Поскольку рассматриваются малые колебания, малыми будут φ1, φ2 , φ1, φ2 . Кинетическая энергия 1 1 1 T J1Oφ2 mVC2 J 2C φ22 , 2 2 2 2 2 ml ml , J 2C где J1O . 3 12 VC VA VCA , VA lφ1 , VCA 0,5lφ 2 . 2 VC2 VA2 VCA 2VAVCA cos φ2 φ1 . ~ 122 ~ Разложим функцию cos φ2 φ1 в степенной ряд cos φ2 φ1 1 φ2 φ1 / 2! ... . Чтобы в выражении кинетической энергии сохранить малые не выше второго порядка, следует в разложении косинуса оставить только первое слагаемое, то есть принять cos φ2 φ1 1. Получим 2 VC2 VA VCA или VC2 l φ1 0,5φ2 . Окончательно 2 2 1 1 4 T ml 2 φ2 φ1φ2 φ22 . 2 3 3 1 Сравнивая с T a11q12 2a12q1q2 a22q22 , найдем 2 4 1 1 a11 ml 2 , a12 ml 2 , a22 ml 2 . 3 2 3 Потенциальную энергию определим как работу сил тяжести при переходе системы из текущего положения в начальное l l П mg 1 cosφ1 mgl 1 cosφ1 mg 1 cosφ2 . 2 2 2 1 φ Приближенно 1 cosφ ; тогда П mgl 3φ12 φ22 . 4 2 1 Сравнивая с П c11q12 2c12 q1q2 c22 q22 , найдем 2 2 1 c11 mgl , c12 0, c22 mgl . 3 2 Значения aik , cik подставим в уравнение частот c 11 a 11 k 2 c22 a22k 2 c12 a 12 k 2 0 . 2 2 g 27 g Уравнение частот примет вид k 6 k 2 0 . l 7 l 4 g g . , k2 2,3 l l Подставляя в одно из уравнений (4) сначала k1 , затем k2 , найдем коэффициенты формы: n1 1,43; n2 2,10 . Таким образом, при первом главном колебании оба стержня в каждый момент времени отклонены от вертикали в одну сторону и Собственные частоты системы k1 0,86 ~ 123 ~ φ1 / φ2 1,43 , а при втором главном колебании – в разные стороны и φ1 / φ2 2,10 (см. рис. 52). 10.8. Вынужденные колебания системы с двумя степенями свободы Пусть на механическую систему, рассмотренную в (10.7), действуют обобщенные непотенциальные силы: Q1 H1 sin t , Q2 H 2 sin t . Дифференциальные уравнения колебаний будут иметь вид a11q1 a12 q2 c11q1 c12 q2 H1 sin t , a12 q1 a22 q2 c12 q1 c22 q2 H 2 sin t. Общее решение этой системы линейных неоднородных дифференциальных уравнений складывается из общего решения соответствующей однородной системы (найдено в 10.7) и частного решения данной неоднородной системы. Частное решение, соответствующее установившимся вынужденным колебаниям, будем искать в виде q1 A1 sin t , q2 A2 sin t . Подставляя это решение в дифференциальные уравнения, приходим к системе алгебраических уравнений для определения амплитуд колебаний A1 , A2 : c c a 112 A1 c12 a122 A2 H1 , 2 2 12 a 12 A1 c22 a22 A2 H 2 . Решение этой системы уравнений имеет вид A1 1 , A2 2 . 11 ~ 124 ~ Здесь определитель, составленный из коэффициентов системы алгебраических уравнений: c11 a 112 c12 a122 a11a22 a122 k12 2 k22 2 , 2 2 c12 a 12 c22 a22 и i определитель, который получается из заменой i -го столбца правыми частями системы уравнений: H1 c12 a122 c11 a 112 H1 ; 1 , 2 2 2 H 2 c22 a22 c12 a 12 H 2 в выражении величины k1 , k2 представляют собой собственные частоты системы. При k1 и при k2 определитель обращается в нуль, и амплитуды неограниченно возрастают. Таким образом, при совпадении частоты возмущающей силы с любой из собственных частот наступает резонанс. Контрольные вопросы 1. Под действием какой силы возникают свободные гармонические колебания материальной точки? 2. Что такое период свободных гармонических колебаний? Как он определяется? 3. От чего зависят амплитуда и начальная фаза свободных гармонических колебаний? 4. Какая сила вызывает затухание свободных колебаний материальной точки? 5. При каком соотношении между круговой частотой k и коэффициентом затухания b материальная точка совершает затухающие свободные колебания? 6. Какие свободные колебания имеют больший период: незатухающие или затухающие? 7. Что определяет декремент колебаний? 8. Какая сила вызывает вынужденные колебания материальной точки? 9. Зависят ли установившиеся вынужденные колебания от начальных условий? 10. Затухают ли установившиеся вынужденные колебания? 11. От каких факторов зависит амплитуда установившихся вынужденных колебаний? 12. Какой случай вынужденных колебаний называется резонансом? ~ 125 ~ 13. Как меняется с течением времени амплитуда вынужденных колебаний в случае резонанса при отсутствии сопротивления среды? 14. Какое положение равновесия называется устойчивым? неустойчивым? Приведите примеры. 15. Сформулируйте теорему Лагранжа – Дирихле, дающую достаточное условие устойчивости положения равновесия механической системы. При каких связях справедлива теорема? 16. Зависят ли собственные частоты k1 , k2 и коэффициенты формы n1 , n2 линейной системы с двумя степенями свободы от начальных условий? 17.При каких условиях наступает резонанс в линейной системе с двумя степенями свободы? Таблица 22 Тестовые задания № 1 2 3 4 Задание/ответ Дифференциальное уравнение свободных колебаний линейной системы с одной степенью свободы имеет вид 1) x k 2 x 0 ; 2) x k 2 x H sin t ; x k 2 x 0 ; 3) 4) x k 2 x Het ; 5) x k 2 sin x 0 . Ответ: 1) Следующие характеристики свободных линейных колебаний не зависят от начальных условий: 1) период колебаний; 2) частота колебаний; 3) круговая частота; 4) амплитуда; 5) начальная фаза колебаний Ответ: 1), 2), 3) Постоянная сила, приложенная к системе, совершающей свободные колебания, изменяет … . 1) положение центра колебаний; 2) период колебаний; 3) амплитуду колебаний; 4) Частоту колебаний; 5) Начальную фазу колебаний Ответ: 1) Консервативная система с одной степенью свободы в положении равновесия q 0 удовлетворяет условиям: 2П П 0, 2 0 q 0 q 0 Равновесие системы … . Ответ: устойчиво ~ 126 ~ 5 6 7 8 9 окончание табл. 22 Дифференциальное уравнение движения системы 2 100q 4π q 0 , период свободных колебаний T ... с . Ответ: 10 Промежуток времени T , в течение которого система совершает одно полное колебание, называется … колебаний. Ответ: периодом Числа n1 , n2 , показывающие, во сколько раз амплитуда соответствующего главного колебания в одной из координат больше (или меньше) амплитуды другой координаты, называются коэффициентами … . Ответ: формы Положение равновесия при z0 mg / c консервативной сис1 темы с потенциальной энергией П mgz cz 2 , где 2 mg 10 H , устойчиво при условии c ... Н/м . Ответ: 0 Движение механической системы определяется уравнением x 100π2 x 0,1sin t резонанс наступит при частоте возмущающей силы … герц. Ответ: 10 11. Принцип Гамильтона - Остроградского 11.1. Общие понятия Под термином «принцип» следует понимать такое аксиоматическое положение, которое, обладая достаточной общностью, является для данной области науки основным, так что все остальные положения вытекают из него как логическое следствие. Принципы механики, устанавливающие какое-либо общее свойство движения для каждого момента времени, называются дифференциальными, а те принципы, которые справедливы только для конечного промежутка времени, называются интегральными. Вариационными называются принципы, которые устанавливают какое-либо свойство истинного движения , отличающее его от всех других воображаемых движений, допускаемых связями и удовлетворяющих некоторым дополнительным условиям. Гамильтон изложил свой принцип в работах 1834 – 1835 годов для свободной системы материальных точек и для системы со стационар- ~ 127 ~ ными связями. Остроградский, не зная работ Гамильтона, опубликованных в мало известных тогда трудах Ирландской Академии наук, в 1848 г. сформулировал принцип в более общей форме, распространив его и на нестационарные связи. По этой причине рассматриваемый принцип называют принципом Гамильтона - Остроградского. Синхронное варьирование. Пусть механическая система имеет одну степень свободы и ее положение определяется обобщенной координатой q f (t ) . Дадим функции q f (t ) при заданном фиксированном t произвольное приращение δq ε φ(t ) , где ε произвольно малое постоянное число, φ(t ) произвольная дифференцируемая функция времени. Получим семейство новых функций времени: q f (t ) ε φ t . Произвольное изменение функции δ(t ) , являющееся следствием не изменения времени, а изменения вида самой функции, называется синхронной вариацией функции: δq q q ε φ t . Рассмотрим голономную консервативную механическую систему. Для такой системы функция Лагранжа L T П . Определенный интеграл от функции Лагранжа по времени носит название действие по Гамильтону: t2 S L dt . t1 S есть функционал, то есть число, величина которого зависит от вида функции L q, q, t . 11.2. Вариационный интегральный принцип Гамильтона-Остроградского Принцип Гамильтона-Остроградского: При перемещении консервативной системы, подчиненной идеальным голономным связям,из одного заданного положения в другое, истинное движение отличается от всех других кинематически допустимых движений тем, что для этого движения действие по Гамильтону имеет стационарное значение: t2 t2 t1 t1 δS 0, или δ L dt 0, или δL dt 0 . Пример. Механическая система состоит из обращенного математического маятника массой m и длиной l и спиральной пружины с ко- ~ 128 ~ эффициентом жесткости C . Найти приближенную зависимость между амплитудой и частотой свободных колебаний (рис. 53). Решение. Для рассматриваемой системы 1 1 T ml 2φ2 , П Cφ2 mgl 1 cosφ . 2 2 Функцию 1 cosφ разложим в степенной ряд и сохраним в разложении первое и второе слагаемые: φ2 φ4 . 1 cosφ 2! 4! Тогда φ2 mgl φ4 П mgl C . 2 6 4 Зададимся формой решения: φ α sin kt . Будем считать α варьируемым параметром: δφ δα sin kt . Вариа2π ция δφ равна нулю при t1 0 и t2 T , где T период колебаний. k Функция Лагранжа 1 2 2 φ2 mgl φ4 L T П ml φ mgl C . 2 2 6 4 Действие по Гамильтону 2π/ k S L dt 0 2π/ k 0 2π/ k ml 2 2 mgl C 2 mgl 4 4 2 α k cos kt sin kt dt α sin kt dt 2 24 2 0 2 2 mgl C α 2 mgl α 4 2 α π kml 2 k 2 8k 4 Варьируем S по α : mgl C mgl 3 δS π kml 2α α α δα 0 . k 8k C mgl g 2 g α , или k 2 k02 α 2 . Находим k 2 2 ml 8l 8l Из выполненного решения видно, что с увеличением амплитуды колебаний частота колебаний возрастает. Из изложенной ранее теории колебаний линейных систем мы знаем, что частота свободных колеба- ~ 129 ~ ний линейной системы не зависит от амплитуды. Почему же в рассматриваемом примере частота зависит от амплитуды? Чтобы получить ответ на этот вопрос, составим дифференциальное уравнение колебаний рассматриваемой системы. Для этого найдем полную механическую энергию системы и продифференцируем ее по времени: U T П const . dU d 1 2 2 φ 2 mgl φ 4 0; ml φ C mgl 0; dt dt 2 2 6 4 mgl 3 φ φ 0. 6 После сокращения на φ получим дифференциальное уравнение колебаний g g C φ 2 φ φ3 0 . l 6l ml Это – нелинейное дифференциальное уравнение. Значит, в данном случае мы имеем дело с нелинейной колебательной системой, чем и объясняются ее особые свойства. Контрольные вопросы ml 2φφ C mgl φφ 1. Какие принципы механики называются дифференциальными? 2. Какие принципы механики называются интегральными? 3. Какие принципы механики называются вариационными? 4. Что понимается под синхронной вариацией функции? 5. Какое выражение называется действием по Гамильтону? 6. Сформулируйте принцип Гамильтона – Остроградского. Таблица 23 Тестовые задания № Задание/ответ t2 1 Интеграл δL dt 0 , где L функция Лагранжа, носит наt1 звание … по Гамильтону Ответ: действие Для истинного движения системы с голономными связями t2 2 вариация действия по Гамильтону δ L dt ... t1 Ответ: 0 ~ 130 ~ окончание табл. 23 3 4 5 Кинетическая энергия системы T 10q 2 , потенциальная – П 8q 2 , функция Лагранжа … . 1) 10q 2 8q 2 ; 2) 10q 2 8q 2 ; 2) 20q 16q ; 2) 20q 16q Ответ: 1) Принцип Гамильтона-Остроградского является интегральным … принципом механики. 1) вариационным 2) дифференциальным 3) изохронным. Ответ: 1) 1 Кинетическая энергия системы T mx 2 , потенциальная 2 1 энергия П Cx 2 , действие по Гамильтону … . 2 t2 1 1 1 1) mx 2 Cx 2 dt 2) ml 2φ2 Cx 2 3) ml 2φ2 Cx 2 2 2 2 t1 Ответ: 1) ~ 131 ~ Список рекомендуемой литературы Учебники: 1. Бутенин Н. В., Лунц Я. Л., Меркин Д. Р. Курс теоретической механики. Т. 2. – СПб.: Лань, 2002. – 496 с. 2. Тарг С. М. Краткий курс теоретической механики. – М.: Высш. шк., 2005. – 416 с. 3. Яблонский А. А. Курс теоретической механики. Ч. 2. Динамика. – 6-е изд. – М.: Высш. шк., 1984. – 423 с. Сборники задач и руководства к решению задач: 4. Кепе О. Э., Виба Я. А., Грапис О. П. и др. Сборник коротких задач по теоретической механике. – М.: Высш. шк., 1989. – 368 с. 5. Яблонский А. А., Норейко С. С., Вольфсон С. А. и др. Сборник заданий для курсовых работ по теоретической механики – 16-е изд. –М.: Интеграл-Пресс, 2008. – 384 с. ~ 132 ~ Оглавление 1. Динамика материальной точки 1.1. Основные понятия и определения 1.2. Законы динамики Галилея-Ньютона 1.3. Дифференциальные уравнения движения материальной точки 1.4. Дифференциальные уравнения относительного движения материальной точки 1.5. Прямые и обратные задачи динамики 2. Введение в динамику механической системы 2.1. Силы внешние и внутренние. Масса системы. Центр масс 2.2. Момент инерции относительно оси. Радиус инерции 2.3. Моменты инерции относительно параллельных осей 2.4. Моменты инерции некоторых однородных тел 2.5. Центробежные моменты инерции 3. Принцип Даламбера (метод кинетостатики) 3.1. Принцип Даламбера для точки и механической системы 3.2.Следствия из принципа Даламбера для механической системы 3.3. Главный вектор и главный момент сил инерции 3.4. Дифференциальные уравнения движения твёрдого тела Индивидуальное задание № 1 Индивидуальное задание № 2 4. Теоремы о движении центра масс и об изменении количества движения механической системы 4.1. Теорема о движении центра масс 4.2. Количество движения материальной точки и системы Импульс силы 4.3. Теорема об изменении количества движения механической системы 5. Теорема об изменении кинетического момента 5.1. Кинетический момент механической системы 5.2. Теорема об изменении кинетического момента относительно неподвижной точки и центра масс системы 6. Теорема об изменении кинетической энергии 6.1. Работа и мощность силы 6.2. Кинетическая и потенциальная энергия 6.3. Теорема об изменении кинетической энергии Индивидуальное задание № 3 Индивидуальное задание № 4 ~ 133 ~ 3 3 3 4 5 8 11 11 11 12 12 13 15 15 15 16 18 21 30 37 37 38 39 41 41 42 46 46 47 48 54 66 7. Аналитическая статика 7.1. Связи 7.2. Виртуальные перемещения 7.3. Идеальные связи 7.4. Принцип виртуальных перемещений Индивидуальное задание № 5 8. Аналитическая динамика 8.1. Обобщенные координаты 8.2. Обобщенные силы 8.3. Уравнения Лагранжа Индивидуальное задание № 6 9. Удар 9.1. Основные положения теории удара 9.2. Коэффициент восстановления (гипотеза Ньютона) 9.3. Теорема об изменении количества движения механической ситемы при ударе 9.4. Теорема об изменении кинетического момента механической системы (теорема моментов) при ударе 10. Колебания 10.1. Устойчивость положения равновесия 10.2. Свободные линейные колебания материальной точки 10.3. Влияние постоянной силы на свободные линейные колебания 10.4. Свободные колебания при вязком сопротивлении (затухающие свободные колебания) 10.5 Вынужденные колебания в линейной системе без сопротивления при гармонической возмущающей силе 10.6. Вынужденные колебания при вязком сопротивлении 10.7. Малые свободные колебания системы с двумя степенями свободы 10.8. Вынужденные колебания системы с двумя степенями свободы 11. Принцип Гамильтона – Остроградского 11.1. Общие понятия 11.2. Вариационный интегральный принцип Гамильтона-Остроградского 12. Список рекомендуемой литературы ~ 134 ~ 74 74 75 75 76 79 86 86 86 88 92 104 104 104 105 106 109 109 110 111 113 115 117 120 124 127 127 128 132