Примеры решения задач семестрового задания. (pdf

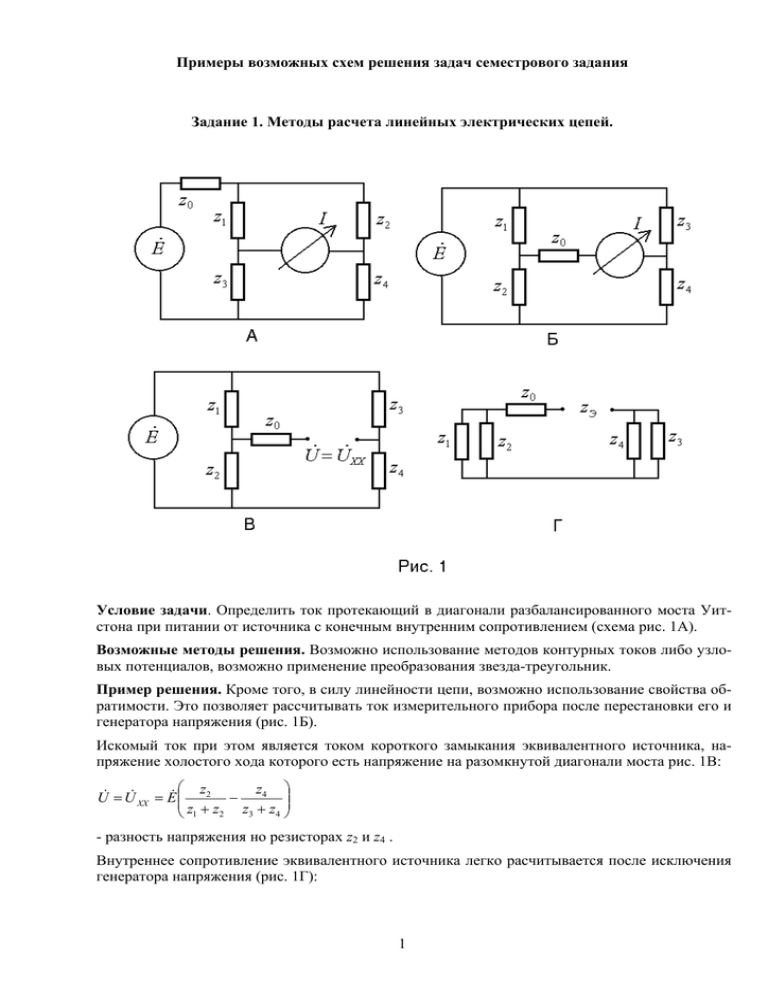
Примеры возможных схем решения задач семестрового задания
Задание 1. Методы расчета линейных электрических цепей.
Условие задачи. Определить ток протекающий в диагонали разбалансированного моста Уитстона при питании от источника с конечным внутренним сопротивлением (схема рис. 1А).
Возможные методы решения. Возможно использование методов контурных токов либо узловых потенциалов, возможно применение преобразования звезда-треугольник.
Пример решения. Кроме того, в силу линейности цепи, возможно использование свойства обратимости. Это позволяет рассчитывать ток измерительного прибора после перестановки его и
генератора напряжения (рис. 1Б).
Искомый ток при этом является током короткого замыкания эквивалентного источника, напряжение холостого хода которого есть напряжение на разомкнутой диагонали моста рис. 1В:
 z
z4 

U& = U& ХХ = E&  2 −
z
z
z
z
+
+
3
4 
 1 2
- разность напряжения но резисторах z2 и z4 .
Внутреннее сопротивление эквивалентного источника легко расчитывается после исключения
генератора напряжения (рис. 1Г):
1
zЭ = z0 + ( z1 || z2 ) + ( z3 || z4 ) = z0 +
z1 z2
zz
+ 3 4
z1 + z2 z3 + z4
(где знак || обозначает параллельное соединение сопротивлений).
Соответственно, комплексная амплитуда тока короткого замыкания эквивалентного источника
и , в силу обратимости, искомого тока будет
I&u = I&КЗ
z2
z4
−
&
U
z1 + z2 z3 + z4
z2 z3 − z1 z4
=
= E&
= E&
.
z1 z2
z3 z 4
(
)(
)
(
)
(
)
zЭ
z
z
+
z
z
+
z
+
z
z
z
+
z
+
z
z
z
+
z
0
1
2
3
4
1
2
3
4
3
4
1
2
z0 +
+
z1 + z2 z3 + z4
Соответственно, действительная величина регистрируемого прибором тока есть I&u .
Задание 2. Колебательный контур.
Условие задачи. Определить частоты ωC и ωL , на которых напряжения на реактивных элементах последовательного колебательного контура (рис. 2) достигают максимумов.
Пример решения. Возможен следующий ход решения. Полное сопротивление RLC-контура
на частоте ω есть

 ω ω0 
1 

 ,
−
z = R + j  ωL −
 = R 1 + jQ 
ωC 

 ω0 ω 

L
1
где ω0 =
- резонансная частота, а Q = C - добротность контура. Соответственно,
R
LC
компленсный коэффициент передачи напряжения источника на емкость есть отношение
комплексного сопротивления емкости к сопротивлению z :
2
KC =
− jxC
=
z
1

 ω ω 
jωC R 1 + jQ  − 0 
 ω 0 ω 

=
− jQ
 ω ω 0 
ω 
1 + jQ  − 
ω0 
 ω 0 ω 
- поскольку комплексная амплитуда приложенного к контуру напряжения есть zI& , а напряжения на емкости − jxC I& , где I& - комплексная амплитуда тока, xC - емкостное сопротивление.
Максимуму напряжения на емкости будет соответствовать максимум модуля этого
коэффициента передачи
Q
KC =
2
 ω
 ω2

  + Q 2  2 − 1
 ω0 
 ω0

2
Q
=
ω
ω2
2
(
)
Q 4 − 2Q − 1 2 + Q 2
ω0
ω0
2
4
,
что для данной дроби может быть найдено как точка минимума подкоренного выражения
ω2
знаменателя как функции отношения x = 2 - т.е. как экстремум соответствующего
ω0
квадратного
x=
Q 2 x 2 − (2Q 2 − 1) x + Q 2 .
трехчлена
Экстремуму
соответствует
точка
2Q − 1
1
= 1−
, что дает частоту
2
2Q
2Q 2
2
ωC = ω0 1 −
1
.
2Q 2
Или, при не слишком малой добротности контура

1 
ωC ≈ 1 −
ω .
2  0
 4Q 
Компленсный коэффициент передачи напряжения источника на индуктивность есть
отношение ее комплексного сопротивления к z
KL =
jxL
=
z
jωL

 ω ω 
R 1 + jQ  − 0 
 ω 0 ω 

=
jQ
ω0
ω

 ω ω 0 
1 + jQ  − 
 ω 0 ω 

- поскольку комплексная амплитуда приложенного к контуру напряжения есть zI& , а напряжения на емкости jx L I& , где I& - комплексная амплитуда тока, xL - емкостное сопротивление.
Максимуму напряжения на индуктивности будет соответствовать максимум модуля
коэффициента передачи
KL =
Q
2
ω2 
 ω0 
2
  + Q 1 − 02 
ω 
 ω 
2
Q
=
Q2
ω 04
ω 02
2
(
)
−
Q
−
+ Q2
2
1
ω4
ω2
- что для данной дроби может быть найдено как точка минимума подкоренного выражения
ω2
знаменателя как функции отношения 02 - что снова сводит задачу к нахождению экстремума
ω
квадратного трехчлена и дает частоту
3
ωL =
ω0
1
1−
2Q 2
.
И, при не слишком малой добротности контура

1 
ωL ≈ 1 +
ω .
2  0
 4Q 
Задание 3. Переходные процессы.
Условие задачи. Для схемы на рис. 3А определить зависимость напряжения на конденсаторе
C от времени после размыкания ключа K. Полагать, что в исходном состоянии резистивный
мост сбалансирован.
Возможные методы решения. Возможно применение классического подхода (построение и
прямое интегрирование дифференциального уравнения переходного процесса), а также использование методов Лапласа или Фурье.
Пример решения. Наиболее компактное решение данной задачи может быть получено при
переходе от исходной схемы к заряду конденсатора от эквивалентного генератора (при замыкании ключа в схеме на рис. 3Б), причем начальные условия на конденсаторе - нулевые (в силу
баланса моста до коммутации). Соответственно, переходной процесс в такой цепи имеет вид
4

t 
uC (t ) = Ei 1 − exp( −
) - заряд конденсатора через сопротивление. Здесь Ei и Ri - ЭДС и
Ri C 

внутреннее сопротивление эквивалентного источника, которые легко могут быть найдены после упрощения исходной схемы (что дает схему рис. 3В).
Напряжение холостого хода на выходе схемы рис. 3В есть U хх = E
телем R1 и R3), а ее выходное сопротивление Ri =
R3
(определяется делиR1 + R3
R1 R3
+ R4 + R5 (делитель R1 и R3 с добавR1 + R3
ленными сопротивлениями R4 и R5 ).
Поскольку Ei=Uхх , то искомый переходной процесс может быть сразу записан как






R3
t
 .
1 − exp −
uC (t ) = E
R
R


R1 + R3 
C ( 1 3 + R4 + R5 ) 


R1 + R3


5