Федотов Н.Г., Фионов Н.С., Курынов Д.А., Старостин В.В., Петренко А.Г..

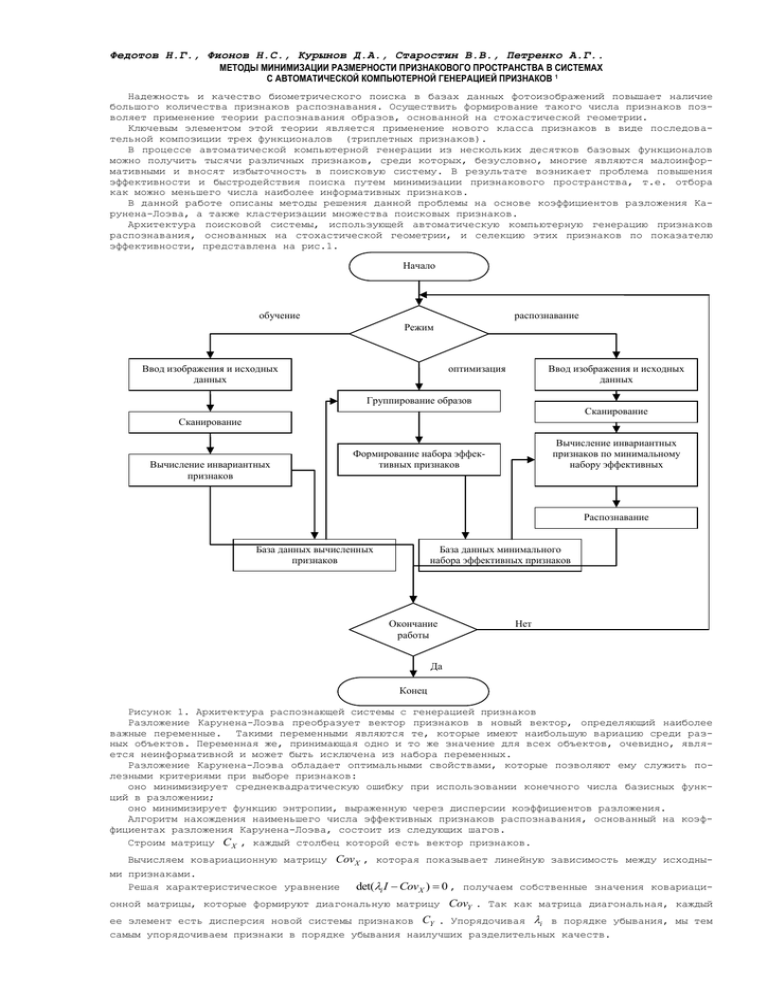
Федотов Н.Г., Фионов Н.С., Курынов Д.А., Старостин В.В., Петренко А.Г..
МЕТОДЫ МИНИМИЗАЦИИ РАЗМЕРНОСТИ ПРИЗНАКОВОГО ПРОСТРАНСТВА В СИСТЕМАХ
С АВТОМАТИЧЕСКОЙ КОМПЬЮТЕРНОЙ ГЕНЕРАЦИЕЙ ПРИЗНАКОВ 1
Надежность и качество биометрического поиска в базах данных фотоизображений повышает наличие
большого количества признаков распознавания. Осуществить формирование такого числа признаков позволяет применение теории распознавания образов, основанной на стохастической геометрии.
Ключевым элементом этой теории является применение нового класса признаков в виде последовательной композиции трех функционалов (триплетных признаков).
В процессе автоматической компьютерной генерации из нескольких десятков базовых функционалов
можно получить тысячи различных признаков, среди которых, безусловно, многие являются малоинформативными и вносят избыточность в поисковую систему. В результате возникает проблема повышения
эффективности и быстродействия поиска путем минимизации признакового пространства, т.е. отбора
как можно меньшего числа наиболее информативных признаков.
В данной работе описаны методы решения данной проблемы на основе коэффициентов разложения Карунена-Лоэва, а также кластеризации множества поисковых признаков.
Архитектура поисковой системы, использующей автоматическую компьютерную генерацию признаков
распознавания, основанных на стохастической геометрии, и селекцию этих признаков по показателю
эффективности, представлена на рис.1.
Начало
обучение
распознавание
Режим
Ввод изображения и исходных
данных
оптимизация
Ввод изображения и исходных
данных
Группирование образов
Сканирование
Сканирование
Вычисление инвариантных
признаков
Вычисление инвариантных
признаков по минимальному
набору эффективных
Формирование набора эффективных признаков
Распознавание
База данных вычисленных
признаков
База данных минимального
набора эффективных признаков
Окончание
работы
Нет
Да
Конец
Рисунок 1. Архитектура распознающей системы с генерацией признаков
Разложение Карунена-Лоэва преобразует вектор признаков в новый вектор, определяющий наиболее
важные переменные. Такими переменными являются те, которые имеют наибольшую вариацию среди разных объектов. Переменная же, принимающая одно и то же значение для всех объектов, очевидно, является неинформативной и может быть исключена из набора переменных.
Разложение Карунена-Лоэва обладает оптимальными свойствами, которые позволяют ему служить полезными критериями при выборе признаков:
оно минимизирует среднеквадратическую ошибку при использовании конечного числа базисных функций в разложении;
оно минимизирует функцию энтропии, выраженную через дисперсии коэффициентов разложения.
Алгоритм нахождения наименьшего числа эффективных признаков распознавания, основанный на коэффициентах разложения Карунена-Лоэва, состоит из следующих шагов.
Строим матрицу C X , каждый столбец которой есть вектор признаков.
Вычисляем ковариационную матрицу CovX , которая показывает линейную зависимость между исходными признаками.
det(i I  CovX )  0 , получаем собственные значения ковариациРешая характеристическое уравнение
онной матрицы, которые формируют диагональную матрицу CovY . Так как матрица диагональная, каждый
ее элемент есть дисперсия новой системы признаков CY . Упорядочивая i в порядке убывания, мы тем
самым упорядочиваем признаки в порядке убывания наилучших разделительных качеств.
Для каждого собственного значения, решая (i I  CovX )wi  0 , получаем собственные вектора и находим новые линейно независимые признаки CY  СX W .
Зная информативность каждого признака, требуется исключить малоинформативные признаки. Для
T
этого находим сумму всех дисперсий S 
n
j
и в набор эффективных признаков включаем признаки до
j 1
тех пор, пока не достигнуто kS. Те признаки, которые вошли в систему, считаются эффективными, а
те, которые не вошли, малоинформативными. Экспериментальным путем установлено, что оптимальное
значение k есть 0.8  k  0.95 в зависимости от требуемой точности решения задачи распознавания.
Отметим, что данная процедура определения минимального набора эффективных признаков имеет явную физическую интерпретацию. Согласно гипотезе компактности, реализация одного и того же класса
образов отражается в признаковом пространстве в геометрически близкие точки, образующие компактные сгустки. Признак считается эффективным, если он разделяет образы разных классов. В нашем случае значения дисперсий – это показатели разделяющей силы признака, т.е. предлагается отбросить
все те признаки, которые практически не разделяют классы.
Другой метод выбора признаков основан на использовании понятия внутреннего расстояния множества. Такой подход используется в задачах кластеризации множеств, который также применим в задаче
принятия решения по исключению малоинформативных признаков.
Расстояние между точками определяется как метрика Евклида:
n
 (ak  bk )2 ,
D ( a, b) 
k 1
где ak и bk суть n-мерные векторы.
Расстояние между точкой и множеством определяется как среднеквадратичное расстояние между точкой и элементами множества:
1 K n
 ( xk  akt )2 ,
K i 1 k 1
D 2 ( x, at ) 
Внутримножественное расстояние определяется как удвоенная сумма выборочных дисперсий объектов
множества:
n
D 2  2 ( k )2 ,
k 1
Принцип кластеризации множества поисковых признаков заключается в том, что множество признаков
представляется в виде векторного пространства, в котором не все измерения характеристик признака
в равной степени важны для определения класса, к которому принадлежат сходные признаки. Процесс
минимизации заключается в сокращении размерности векторного пространства поисковых признаков. При
сопоставлении двух признаков последовательным сравнением их характеристик измерениям с меньшей
значимостью следует приписать меньшие веса. Назначение весов признаков можно осуществить посредством линейного преобразования, которое обеспечит более благоприятную группировку точек признаков
в новом пространстве. Линейное преобразование представляет собой матричный оператор весовых коэффициентов:
 w11

W 
w
 n1
w1n 

,
wnn 
Используя определение внутримножественного расстояния, можно определить внутреннее расстояние
для множества точек, представляющих признаки, в новом пространстве:
n
D 2  2 ( wkk k ) 2 .
k 1
Рассмотрим два случая ограничения весовых коэффициентов для осуществления процедуры минимизации.
n
В случае ограничения
 wkk  1
весовой коэффициент признака определяется по формуле
k 1
wkk 
1
 k2
n
1
 ( 2 )
k 1
,
k
n
В случае ограничения
 wkk  1
весовой коэффициент признака определяется выражением:
k 1
wkk 
1
k
n
1
( j ) n .
j 1
Таким образом, применение линейного преобразования с вычисленными по представленным выше выражениям весами позволит минимизировать расстояния между точками (объектами) признакового пространства. Затем полученную матрицу точек пространства поисковых признаков необходимо привести к диагональному виду. В таком случае элементами полученной диагональной матрицы будут несмещенные
оценки выборочной дисперсии, что позволит выделить элементы, имеющие малую (или наоборот большую)
дисперсию, и на основании этого исключить малоинформативные или избыточные признаки.
Описанные методы минимизации размерности признакового пространства позволяют повысить быстродействие распознавания и применять наиболее простые решающие процедуры. Работа выполнена при поддержке гранта РФФИ №09-07-00089.
Литература
1. Федотов Н.Г. Теория признаков распознавания образов на основе стохастической геометрии и
функционального анализа. - М.: ФИЗМАТЛИТ, 2009.
2. Julius T. Tou, Rafael C. Gonzalez. Pattern Recognition Principles. Addison-Wesley Publishing Copany, 1974.
3. Mark S. Nixon, Alberto S. Aguado. Feature Extraction and Image Processing. Second edition.
Elsevier, 2008.