Тема 5. Исследование остатков модели

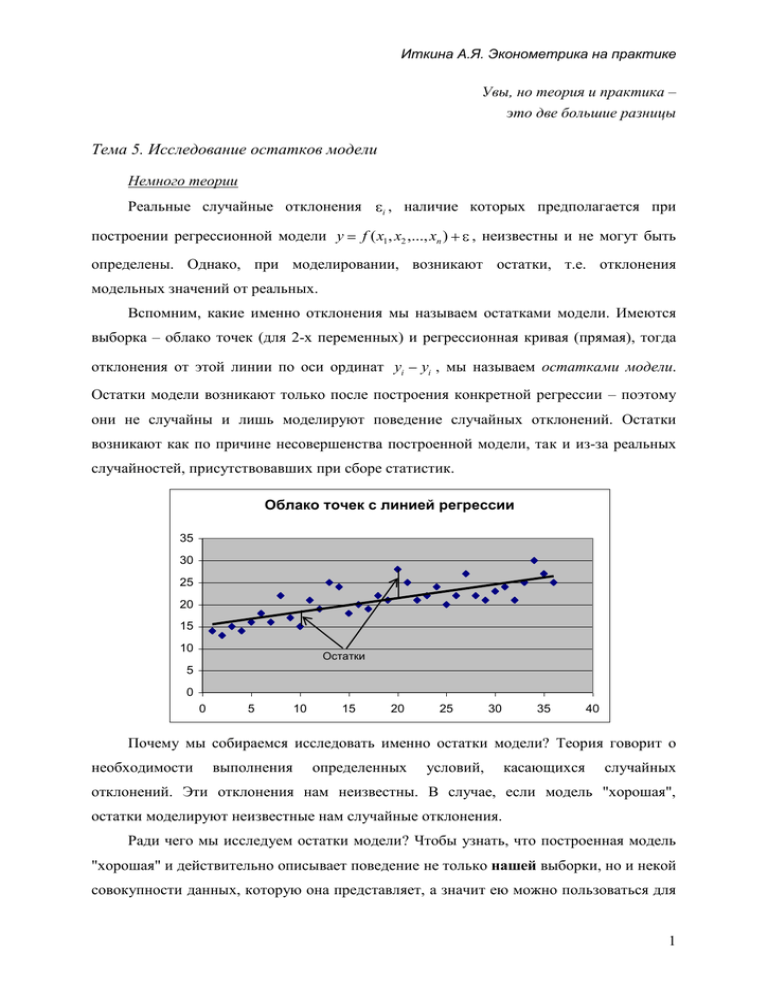
Иткина А.Я. Эконометрика на практике
Увы, но теория и практика –
это две большие разницы
Тема 5. Исследование остатков модели
Немного теории
Реальные случайные отклонения
построении регрессионной модели y
i
, наличие которых предполагается при
f ( x1 , x2 ,..., xn )
, неизвестны и не могут быть
определены. Однако, при моделировании, возникают остатки, т.е. отклонения
модельных значений от реальных.
Вспомним, какие именно отклонения мы называем остатками модели. Имеются
выборка – облако точек (для 2-х переменных) и регрессионная кривая (прямая), тогда
отклонения от этой линии по оси ординат yi
yi , мы называем остатками модели.
Остатки модели возникают только после построения конкретной регрессии – поэтому
они не случайны и лишь моделируют поведение случайных отклонений. Остатки
возникают как по причине несовершенства построенной модели, так и из-за реальных
случайностей, присутствовавших при сборе статистик.
Облако точек с линией регрессии
35
30
25
20
15
10
Остатки
5
0
0
5
10
15
20
25
30
35
40
Почему мы собираемся исследовать именно остатки модели? Теория говорит о
необходимости
выполнения
определенных
условий,
касающихся
случайных
отклонений. Эти отклонения нам неизвестны. В случае, если модель "хорошая",
остатки моделируют неизвестные нам случайные отклонения.
Ради чего мы исследуем остатки модели? Чтобы узнать, что построенная модель
"хорошая" и действительно описывает поведение не только нашей выборки, но и некой
совокупности данных, которую она представляет, а значит ею можно пользоваться для
1
Тема 5. Исследование остатков модели
целей анализа и/или прогноза. Дело в том, что метод наименьших квадратов обещает
дать качественные оценки коэффициентов регрессии лишь в случае выполнения
некоторых
ограничений,
наложенных
на
случайные
отклонения.
В
рамках
классической линейной модели случайные отклонения должны обладать следующими
свойствами (предпосылки МНК или условия Гаусса-Маркова):
1. Математическое ожидание случайного отклонения
i
равно нулю для всех
наблюдений.
2. Дисперсия случайных отклонений
i
одинакова для всех наблюдений.
3. Случайные отклонения
i
и
4. Случайные отклонения
i
независимы от объясняющих переменных.
j
независимы друг от друга для всех i
j.
5. Модель линейна относительно параметров (коэффициентов).
6. Дополнительные условия:
случайные отклонения имеют нормальное распределение;
число наблюдений значительно больше числа объясняющих переменных;
отсутствует линейная зависимость между объясняющими переменными.
Поскольку мы предполагаем, что остатки моделируют случайные отклонения,
выполнение свойств Гаусса-Маркова будет проверяться на остатках модели.
Равенство 0 математического ожидания случайного отклонения
Поскольку мы имеем только одну выборку, мы вынуждены сравнивать
единственное выборочное математическое ожидание с нулем. И тогда, в случае, если в
модели присутствует свободный член, выборочное среднее обязательно будет равно
нулю. Однако этого бывает недостаточно. На рисунке представлен пример, в котором
Области заниженных оценок
+
+
M( )
–
Область завышенных оценок
Облако точек
График остатков
Рис. 1. Непостоянное математическое ожидание остатков модели
2
0
Иткина А.Я. Эконометрика на практике
выборочное среднее равно нулю, но существуют значительные области, где оно
отлично от нуля. Таким образом, если разбить наблюдения на несколько областей, они
не будут описываться общей линией регрессии.
По рис. 1 видно, что имеется область графика, где модель дает завышенные
прогнозы
y , а имеются области, где прогнозы занижены. Т.е. последствием
неравенства математического ожидания остатков 0 будут неверные – смещенные
оценки модели.
Основной причиной невыполнения 1-й предпосылки
МНК является неверная спецификация модели. Например,
эти точки можно описать с помощью двух линейных
зависимостей или нелинейной. Однако существуют и
другие причины, вызывающие нарушение 1-й предпосылки
(рис. 2).
Выбросом
называется резко отличающееся от всей
выборки наблюдение. Обычно считается,
+
–
что наблюдение является выбросом, если
Смещенная линия
регрессии
оно отличается от среднего y более чем на
2
для небольших выборок и более чем на
3
для выборок объемом более 300
наблюдений.
Выброс
Рис. 2. Смещенные оценки коэффициентов
Возникает вопрос, как можно обнаружить нарушение предпосылки о равенстве 0
математического ожидания остатков. Изучение графика остатков модели (рис. 1) могло
бы помочь увидеть, что имеются области с положительными и области с
отрицательными остатками. Но ведь остатки могут быть изображены в произвольном
порядке, т.е. их график зависит от того, в каком порядке записаны наблюдения в
выборке. Поэтому прежде чем изучать график или применять какой-либо тест,
необходимо упорядочить данные, а вместе с ними и остатки, в порядке возрастания
самой важной объясняющей переменной.
Постоянство дисперсии случайных отклонений
Опять же, имея лишь одну выборку, мы проверяем это условие, рассчитывая
дисперсию остатков. Каждый конкретный остаток может быть большим или
3
Тема 5. Исследование остатков модели
маленьким, но не должно быть причины, приводящей к росту или падению величины
дисперсии. Выполнение этого условия называется гомоскедастичность, а невыполнение
– гетероскедастичность. Последствием гетероскедастичности
является неверное
оценивание дисперсии коэффициентов регрессии, что, в свою очередь, не позволяет
правильно оценить их значимость и построить для них верные доверительные
интервалы. Соответственно оценки коэффициентов регрессии будут неэффективными.
Причиной, вызывающей нарушение этой предпосылки МНК, может оказаться
неоднородность исходных данных. Например, каждые 10 минут проводились замеры
напряжения в электрической сети. Потом был установлен сетевой фильтр или
устройство бесперебойного питания (УБП), которое срезает пики напряжения, и
замеры были продолжены. Одинаково ли хорошо будет описывать линия регрессии
наблюдения до включения УБП и после него?.. Одинаковой ли надежностью будет
обладать регрессия, построенная по всем наблюдениям, без учета различий?
Колебания напряжения в электрической розетке
230
225
220
215
210
205
0
10
20
30
40
50
Обнаружить наличие гетероскедастичности можно по графику остатков;
предположить ее наличие, исходя из условий сбора данных; воспользовавшись тестами,
некоторые из которых будут описаны ниже.
Отсутствие автокорреляции случайных отклонений
Корреляция – это линейная зависимость между переменными. Автокорреляция –
зависимость между различными значениями одной и той же переменной. В данном
случае зависимость одного остатка от другого.
Представить себе это можно так (рис. 3)
4
Иткина А.Я. Эконометрика на практике
I
+
+
–
II
–
Положительная автокорреляция остатков
Отрицательная автокорреляция остатков
Рис. 3. Автокорреляция остатков
То есть мы можем увидеть в первом случае много положительных остатков и
много отрицательных подряд. Имеющаяся тенденция к сохранению знака остатка,
может быть объяснена зависимостью ei
ei 1 , где
0 . А на втором рисунке можно
наблюдать почти строгое чередование знаков остатков, что можно представить как
ei
ei 1 , где
0 . Таким образом можно предположить, что часть зависимости не
попала в построенную функцию (не отражается уравнением регрессии).
Последствиями автокорреляции будут неэффективные оценки коэффициентов
регрессии.
К основным причинам автокорреляции остатков стоит отнести неверную
спецификацию модели, т.е. неверный вид зависимости или потерю важных
объясняющих переменных. Наличие выброса в исходных данных также может
привести к автокорреляции остатков. Как же ее можно обнаружить?
Иногда автокорреляцию можно обнаружить по графику остатков. А также
существует несколько специальных тестов. Однако и график и тесты могут показать
ложную корреляцию, а могут не обнаружить реальную. На первом графике
представлена зависимость цены телевизора от его диагонали. На этом графике
отчетливо видна положительная автокорреляция остатков.
5
Тема 5. Исследование остатков модели
На втором графике изображена зависимость величины остатка от его порядкового
номера. По графику автокорреляция не прослеживается. Можно утверждать лишь
наличие выброса.
Причиной такого несоответствия снова является порядок, в котором изображены
остатки модели. Упорядочим выборку по возрастанию основной объясняющей
переменной
–
диагональ.
Снова
построим ту же модель и рассмотрим
график остатков.
Теперь
показывает
график
остатков
ясно
наличие
положительной
автокорреляции.
Случайные отклонения независимы от объясняющих переменных
Чаще всего это условие выполняется автоматически, поскольку объясняющие
переменные являются неслучайными. В случае нарушения этого свойства оценки
коэффициентов являются смещенными.
Модель линейна относительно параметров
Выполнение этого свойства необходимо для решения системы нормальных
уравнений и получения однозначных оценок коэффициентов. Поскольку вид модели
задается исследователем, эта предпосылка всегда может быть выполнена.
Нормальное распределение случайных отклонений
Это требование не является строгим. Однако его выполнение позволяет
исследователю пользоваться формулами для расчета доверительных интервалов для
коэффициентов и зависимой переменной у, которые были приведены выше. Да и
выводам, получаемым с помощью критериев Фишера, Стьюдента и др. можно доверять
при условии нормального распределения остатков (при не очень больших n).
Однако многие критерии являются устойчивыми к небольшому отклонению
распределения
случайной
величины
от
нормального.
Требование
близости
распределения остатков к нормальному закону распределения оказывается понятным в
следующей формулировке: маленьких остатков должно быть много, а больших мало.
6
Иткина А.Я. Эконометрика на практике
Гистограмма выборки, имеющей нормальное
распределение
14
12
10
8
6
4
2
0
1
-3 2
-2 3
-14
50
61
7 2
8 3
9
4 10
Число наблюдений больше числа объясняющих переменных
Это требование вызвано необходимостью решать систему из (k+1) уравнения с
(k+1) неизвестным, где k – объясняющих переменных + 1 свободный член. При этом
решение будет устойчивым только в случае значительного (хотя бы в 3 раза)
превышения числа наблюдений над числом переменных.
Отсутствует линейная зависимость между объясняющими переменными
В случае присутствия такой зависимости одну переменную можно выразить через
другую. А соответствующие уравнения в системе окажутся линейно зависимыми.
Система из (k) уравнений с (k+1) неизвестным не имеет однозначного решения. Т.е.
МНК неприменим.
Если все условия теоремы Гаусса-Маркова выполнены, то утверждается, что
оценки коэффициентов будут несмещенными, состоятельными и эффективными.
Но … Поскольку количество замеров всегда ограничено, более того обычно мы
располагаем только одной выборкой из генеральной совокупности, а не десятком, то в
реальности важно лишь то, что модель будет адекватно описывать именно наши
данные, и что доверительные интервалы для коэффициентов модели и для регрессии в
целом будут построены верно, т.е. с большой вероятностью будут накрывать реальные
значения соответствующих параметров.
Исследование остатков в Eviews
Перед тем как обратиться к математическим методам проверки предпосылок
МНК, желательно посмотреть на график остатков и визуально оценить его. В окне
7
Тема 5. Исследование остатков модели
уравнения справа есть кнопка Resids или в меню View, далее Actual,Fitted,Residual,
далее Residual Graph мы можем получить график остатков в виде ломаной,
соединяющей последовательные остатки. Не всегда все свойства остатков можно
увидеть на графике. Но часто можно заметить наличие автокорреляции остатков
3000
или, как видно на представленном
2000
здесь
рисунке,
наличие
гетероскедастичности.
1000
Теперь
0
воспользуемся
встроенными в Eviews тестами
-1000
для того, чтобы проверить все
-2000
10
20
30
40
50
60
70
80
90
упомянутые свойства остатков.
Проверить
PRICE Res iduals
равенство
математического ожидания остатков нулю в Eviews можно, например, с помощью
Simple Hypothesis Tests. Этот тест доступен, если переменную resid открыть как
группу, например двойным щелчком. В меню группы нужно выбрать View, затем Tests
for Descriptive Stats, а там Simple Hypothesis Tests. Слева в поле Mean вводим 0, т.е.
проверяемую нами величину математического ожидания.
Поскольку для модели в целом (при включении в модель свободного члена)
математическое ожидание остатков равно нулю по построению, такая проверка
выглядит бессмысленной. Поэтому для более корректной проверки следует поменять
Sample, поделив выборку хотя бы на 2 части. Для этого в горизонтальном меню
выбираем Sample, уменьшаем правую границу интервала, нажимаем Ok. Проводим
Simple Hypothesis Tests и анализируем полученный результат. В приведенном примере
значение t-статистики близко к 0, а вероятность больше стандартного уровня
значимости
=0.05, поэтому мы условно принимаем
(нет оснований отвергнуть)
гипотезу о равенстве мат. ожидания первой подвыборки 0. Аналогично, меняя Sample,
рассматриваем
подвыборку
вторую
остатков
первоначальной выборки. Тем
самым
мы
отсутствии
областей,
убеждаемся
в
значительных
где
математическое
ожидание отлично от нуля. Эту
8
Иткина А.Я. Эконометрика на практике
проверку имеет смысл проводить лишь в случае упорядоченности наблюдений в
порядке возрастания самой важной объясняющей переменной.
Следующим тестом, к которому мы обратимся будет Residual Test под названием
White Heteroskedasticity (no сross terms).
White Heteroskedasticity Test:
F-statistic
Obs*R-squared
14.58521
31.03563
Probability
Probability
0.000000
0.000001
Test Equation:
Dependent Variable: RESID^2
Method: Least Squares
Date: 04/02/10 Time: 23:02
Sample: 1 97
Included observations: 97
Variable
Coefficient
Std. Error
t-Statistic
Prob.
C
SPACE
SPACE^2
TIME
-481519.7
9633.105
-10.77859
-58394.22
219774.7
3100.206
8.591898
153978.4
-2.190970
3.107247
-1.254507
-0.379236
0.0310
0.0025
0.2128
0.7054
R-squared
Adjusted R-squared
S.E. of regression
Sum squared resid
Log likelihood
Durbin-Watson stat
0.319955
0.298018
708523.6
4.67E+13
-1442.276
2.174922
Mean dependent var
S.D. dependent var
Akaike info criterion
Schwarz criterion
F-statistic
Prob(F-statistic)
297925.6
845651.4
29.82012
29.92629
14.58521
0.000000
Проверяемая гипотеза формулируется так: дисперсия остатков постоянна. В
теории утверждается постоянство дисперсии для каждого
i
. Однако, в реальности
обычно имеется лишь одна выборка. Для этой выборки рассчитываются значения
критерия Фишера (F-statistic) и критерия Obs*R-squared (асимптотически имеет
рапределение хи-квадрат). Соответствующие им значения вероятностей написаны
справа. Если вероятности больше уровня значимости, мы условно принимаем гипотезу
о постоянстве дисперсии остатков модели (гомоскедастичность), в противном случае
мы эту гипотезу отвергаем, что говорит о гетероскедастичности остатков.
В
нижней
части
теста
расположена
таблица,
в
которой
рассчитана
вспомогательная регрессия квадрата остатков RESID^2 на переменные из основной
модели в первой и второй степени (т.е. на хi и на хi2). При наличии
гетероскедастичности эта регрессия окажется значимой. И если определить значимые
переменные, то можно предположить, что
2
пропорциональна хi или хi2. Тогда можно
преобразовать исходные данные для последующего применения ВНК (взвешенного
метода наименьших квадратов). В данном примере можно попробовать разделить все
исходные данные на SPACE. К ВНК можно обратиться через командную строку
9
Тема 5. Исследование остатков модели
LS(w=SPACE) price=c(1)*SPACE+c(2)*Time+C(3) или задав опции (Options) в окне
уравнения.
Есть
и
другие
гетероскедастичностью,
методы
борьбы
например
с
иногда
можно использовать фиктивные переменные.
Следующим тестом, который будет рассмотрен является тест Дарбина-Уотсона на
автокорреляцию. В окне уравнения представлена (если в модели присутствует
свободный член) статистика Durbin-Watson stat. Сравнив полученное значение с
табличными границами, можно принять решение о наличии или отсутствии
автокорреляции первого порядка, т.е. зависимости между последовательными
остатками.
область, где автокорреляция отсутствует
dl
0
+
4-dl
du
2
4-du
область, где автокорреляция положительна
4
–
область, где автокорреляция отрицательна
Для выбранного заранее уровня значимости и n-m степеней свободы находим по
таблице нижний и верхний пределы статистики Дарбина-Уотсона. Если вычисленное
значение статистике оказывается в первом интервале (близко к нулю), делается вывод о
наличие положительной автокорреляции первого порядка. Если оно оказывается
близко к 2, гипотеза о равенстве 0 автокорреляции условно принимается. При
попадании в интервал около 4 делается вывод об отрицательной автокорреляции
остатков модели. При попадании в интервалы (dl;du) или (4-du;4-dl) критерий не дает
ответа о присутствии или отсутствии автокорреляции.
Поскольку существуют области неопределенности в критерии Дарбина-Уотсона,
а также существует опасность наличия автокорреляции более высоких порядков, чтобы
10
Иткина А.Я. Эконометрика на практике
судить об отсутствии автокорреляции в целом мы рассмотрим еще один критерий
проверки равенства автокорреляции 0.
Из окна уравнения доступен пункт меню этого окна View, далее Residual Tests,
далее Correlogram – Q-statistics. С предложенным количеством лагов можно
согласиться. Далее получаем следующую таблицу
В данной таблице первые два столбца занимает графическое представление
автокорреляции и частной корреляции того порядка, который дан в третьем столбце.
При этом нарисованы границы, в пределах которых корреляцию можно считать
незначимой. В четвертом и пятом столбцах даны сами значения коэффициентов
автокорреляции и частной корреляции соответствующего порядка. В шестом столбце с
заголовком
Q-Stat
даны
значения
статистики
Льюнга-Бокса.
Эта
статистика
используется для принятия решения о значимости или незначимости конкретного
коэффициента автокорреляции при имеющемся количестве наблюдений и выбранном
порядке автокорреляции. Гипотеза, которую мы проверяем – это снова простая
гипотеза в виде равенства: автокорреляция остатков всех порядков до i-го равна 0.
Сравнивая значение вероятности в последнем столбце с уровнем значимости
(например 0.05), можно принять решение о наличии автокорреляции 1-го порядка и об
отсутствии автокорреляции 2-го порядка в данном примере.
Частные коэффициенты корреляции, например 3-го порядка, представляют собой
корреляцию между остатками 1-м и 4-м, 2-м и 5-м и т.д., "очищенную" от влияния
промежуточных значений остатков.
11
Тема 5. Исследование остатков модели
Обратимся теперь к Residual Test под названием Histogram – Normality Test.
В правой части окна мы видим следующую информацию об остатках:
Mean
-2.26E-12 – среднее значение (или оценка мат.ожидания остатков);
Median
-23.17979 – выборочная медиана остатков;
Maximum 2573.330 – максимальное значение, встречающееся среди остатков;
Minimum -1685.540 – соответственно минимальное значение;
Std. Dev.
548.6610 – выборочное стандартное отклонение остатков;
Skewness
1.253111 – выборочная асимметрия (третий момент выборки из
остатков, деленный на Std. Dev.3), характеризует взаимное расположение среднего
значения и медианы. У нормального распределения асимметрия = 0, поскольку оно
симметрично.
Kurtosis
характеризует
8.973825 – эксцесс (четвертый момент, деленный на Std. Dev.4),
форму
вершины
распределения
остатков.
Для
нормального
распределения эксцесс = 3. В данном случае мы имеем островершинное распределение
остатков.
Для проверки согласия выборки с нормальным распределением можно
пользоваться тестом Жарка-Бера.
Jarque-Bera 169.6196 – статистика Жарка-Бера, рассчитанная исходя из значений
ассиметрии и эксцесса.
Probability 0.000000 – вероятность, соответствующая статистике Жарка-Бера.
В приведенном примере мы вынуждены отвергнуть гипотезу о нормальном
распределении остатков.
Теперь посмотрим на гистограмму.
Отрезок [Minimum, Maximum] разбит на
несколько интервалов, которые изображены на оси абсцисс, а количество остатков,
попавших в соответствующий интервал, отражается на оси ординат.
Глядя на гистограмму (или на график остатков), можно иногда увидеть сильно
выделяющийся по величине остаток (выброс). И хотя редкие события иногда
происходят, стоит задуматься, столкнулись ли мы с таким событием или данное
наблюдение попало в выборку по ошибке. Найти, какому именно наблюдению
соответствует такое значение остатка, можно открыв переменную Resid. Также удобно
увидеть такой скачок, открыв таблицу в меню View, далее Actual,Fitted,Residual, далее
Actual,Fitted,Residual Table.
Казалось бы, что может испортить одно наблюдение из n? Когда выборка невелика, мы
получим смещенные оценки всех коэффициентов. Для большой выборки влияние одного
12
Иткина А.Я. Эконометрика на практике
наблюдения мало, но стоит не забывать, что в МНК минимизируются квадраты отклонений, а
когда отклонение велико, то его квадрат может оказаться весьма значительным числом, и
качество модели может от этого пострадать. НО выбросов не бывает много. Если вам хочется
назвать выбросами более 3% наблюдений – задумайтесь. Эти данные – реальные. Значит не
данные плохи, а ваша модель неверно их описывает.
Если вы приняли решение считать конкретное наблюдение выбросом, его следует
удалить из выборки, по которой вы проводите моделирование. Для этого выделяем все
имеющиеся переменные в группу. Находим нужную строку, которую собираемся
удалять, выделяем ее, нажимаем на кнопку InsDel в горизонтальном меню окна.
Выбираем опцию удаления, при этом в левом углу в окошке записан номер записи,
которую мы будем удалять. Нажимаем ОК, и соответствующая запись удаляется.
Теперь можно начинать построение зависимости заново.
Итак, если все тесты остатков оказались пройдены, можно утверждать, что
модель адекватно описывает наблюдения и ей можно пользоваться. Хочется здесь
отметить, что если вы придаете большое значение выводам, которые могут быть
получены на основе построенной модели, то стоит использовать несколько разных
тестов, для более уверенного и обоснованного вывода о качестве модели.
Литература:
1. Бородич С.А. Эконометрика. Учебное пособие. – Минск: Новое знание, 2006. – 407 с.
2. Доугерти К. Введение в эконометрику. - М.: ИНФРА-М, 2009. – 413 с.
13