Часть 1. Механика. Электричество

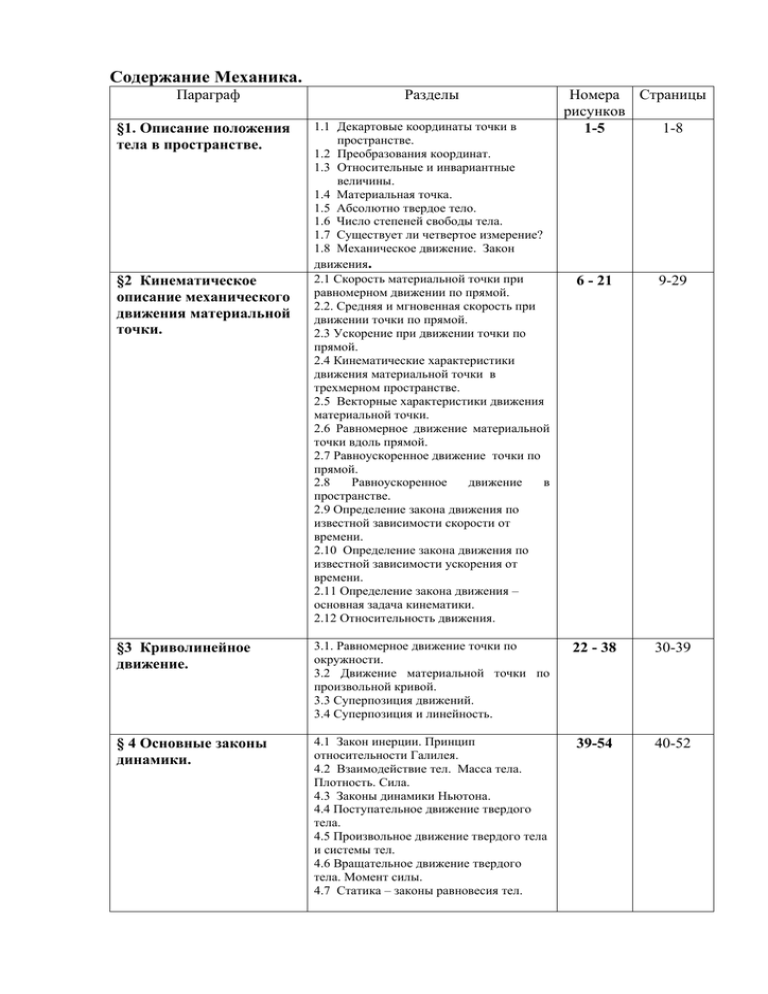
Содержание Механика.
Параграф
§1. Описание положения
тела в пространстве.
§2 Кинематическое
описание механического
движения материальной
точки.
Разделы
1.1 Декартовые координаты точки в
пространстве.
1.2 Преобразования координат.
1.3 Относительные и инвариантные
величины.
1.4 Материальная точка.
1.5 Абсолютно твердое тело.
1.6 Число степеней свободы тела.
1.7 Существует ли четвертое измерение?
1.8 Механическое движение. Закон
движения.
2.1 Скорость материальной точки при
равномерном движении по прямой.
2.2. Средняя и мгновенная скорость при
движении точки по прямой.
2.3 Ускорение при движении точки по
прямой.
2.4 Кинематические характеристики
движения материальной точки в
трехмерном пространстве.
2.5 Векторные характеристики движения
материальной точки.
2.6 Равномерное движение материальной
точки вдоль прямой.
2.7 Равноускоренное движение точки по
прямой.
2.8
Равноускоренное
движение
в
пространстве.
2.9 Определение закона движения по
известной зависимости скорости от
времени.
2.10 Определение закона движения по
известной зависимости ускорения от
времени.
2.11 Определение закона движения –
основная задача кинематики.
2.12 Относительность движения.
Номера Страницы
рисунков
1-8
1-5
6 - 21
9-29
§3 Криволинейное
движение.
3.1. Равномерное движение точки по
окружности.
3.2 Движение материальной точки по
произвольной кривой.
3.3 Суперпозиция движений.
3.4 Суперпозиция и линейность.
22 - 38
30-39
§ 4 Основные законы
динамики.
4.1 Закон инерции. Принцип
относительности Галилея.
4.2 Взаимодействие тел. Масса тела.
Плотность. Сила.
4.3 Законы динамики Ньютона.
4.4 Поступательное движение твердого
тела.
4.5 Произвольное движение твердого тела
и системы тел.
4.6 Вращательное движение твердого
тела. Момент силы.
4.7 Статика – законы равновесия тел.
39-54
40-52
§5. Виды
взаимодействий.
§6. Законы сохранения в
механике.
5.1 Гравитационные взаимодействия.
Закон всемирного тяготения Ньютона.
5.2 Сила тяжести.
5.3 Силы упругости. Закон Гука.
5.4 Силы реакции.
5.5 Силы сухого трения.
5.6 Силы вязкого трения.
6.1 Импульс тела. Закон сохранения
импульса.
6.2 Закон сохранения момента импульса.
6.3 Работа. Кинетическая энергия.
6.4 Потенциальная энергия.
6.5 Потенциальная энергия тел,
находящихся в поле тяжести.
6.6 Потенциальная энергия
деформированной пружины.
6.7 Потенциальная энергия
гравитационного притяжения.
6.8 Работа сил трения.
6.9 Закон сохранения энергии.
6.10 Заметки о симметрии.
§7. Механика жидкости 7.1 Модель сплошной среды, «точечные»
характеристики вещества.
и газа.
7.2 Кинематическое описание движения
жидкости и газа – «гидрокинематика».
Поле скоростей.
7.3 Поток жидкости.
7.4 Вихревое движение жидкости.
Циркуляция скорости.
7.5 Основные законы гидростатики.
Давление. Закон Паскаля. Закон
Архимеда.
7.6 Движение жидкости - гидродинамика.
Течение жидкости по трубам.
7.7 Давление
жидкости.
в
движущейся
7.8 Распределение давления в идеальной
жидкости,
движущейся
по
горизонтальной трубе.
7.9 Уравнение Бернулли.
7. 10 Движение вязкой жидкости по
горизонтальной трубе.
7.11 Движение вязкой жидкости по
горизонтальному замкнутому контуру.
55-74
53-63
75-99
64-81
100-140
82-104
Содержание. Электростатика.
Параграф
§ 8. Электростатические
взаимодействия.
Электрический заряд.
Закон Кулона.
Разделы
8. 1 Два вида электрических зарядов.
8.2 Закон Кулона.
8.3 Единицы измерения электрического
заряда.
8.4 Закон сохранения электрического
заряда.
8.5 Дискретность электрического заряда.
Объемная плотность заряда.
8.6 Инвариантность электрического
заряда.
8.7 Принцип суперпозиции для
электростатических сил.
§ 9. Электрическое поле и 9.1 Напряженность электрического поля.
9.2 Напряженность электрического поля
его свойства.
Номера Страницы
рисунков
105-113
141-149
150-173
114-126
9.8 Потенциальность
электростатического поля. Потенциальная
энергия взаимодействия электрического
заряда с электрическим полем.
9.9 Потенциал электростатического поля.
9.10 Связь между потенциалом и
напряженностью электрического поля.
9.11 Примеры расчета потенциалов
электростатических полей.
9.12 Электрический диполь.
174-211
127-144
9.13 Энергия электрического поля.
Плотность энергии.
9.14 Энергия поля и энергия
взаимодействия зарядов.
10.1 Проводники.
10.2 Условия равновесия между зарядами
и электрическим полем.
10.3 Применение электростатических
свойств проводников.
212-223
145-153
224-241
154-163
10.4 Расчет поля в присутствии
проводников. Метод изображений.
242-257
164-172
10.5 Диэлектрики. Поляризация
диэлектриков.
10.6 Описание электрического поля в
диэлектриках.
10.7 Метод изображений для
диэлектриков.
11.1 Характеристики электрического тока.
11.2 Закон Ома.
258-267
173- 181
268-293
182-203
точечного заряда.
9.3 Принцип суперпозиции для
напряженности электрического поля.
9. 4 Силовые линии электростатического
поля.
9. 5 Поток вектора напряженности
электрического поля. Теорема Гаусса.
9.6 Поле равномерно заряженной
плоскости.
9.7 Поле равномерно заряженной сферы.
§ 10. Проводники и
диэлектрики в
электростатическом
поле.
§ 11 Постоянный
электрический ток.
11.3 Закон Джоуля-Ленца.
11. 4 Электрическое сопротивление.
11.5 Последовательное соединение
резисторов.
11.6 Параллельное соединение
резисторов.
11.7 Примеры расчета сопротивлений
цепи.
11.8 Электрическое сопротивление среды
при пространственно распределенных
токах.
11.9 Время установления стационарного
тока.
11.10 Условия существования
постоянного электрического
тока в цепи.
11.11 Электродвижущая сила
(ЭДС)
и
внутреннее
сопротивление источника.
11.12 Закон Ома для полной
цепи.
294-298
204-208
Часть 1. Механика.
Механика как раздел физики изучает механическое движение, т. е. изменение
положения тела в пространстве с течением времени.
Основную задачу механики можно сформулировать в виде: «Описать положение
тела в пространстве в произвольный момент времени».
Несмотря на кажущуюся простоту, эта постановка задачи требует существенного
уточнения и конкретизации, т. е. ответа на вопросы (не затрагивая принципиальные
философские проблемы о природе пространства и времени):
1. Каким образом в физике описывается положение точки в пространстве?
2. Что мы понимает под термином «тело»?
3. Как описать изменение положения тела?
Ответы на эти вопросы дает «кинематика» - раздел механики, математически
описывающий движения тел, не рассматривая причины того или иного движения.
§1. Описание положения тела в пространстве.
1.1 Декартовые координаты точки в пространстве.
Положение (место) точки в пространстве математически удобно описывать с
помощью чисел – координат. Простейшей системой (и хорошо вам знакомой) координат
является прямоугольная декартовая система. Для ее
построения необходимо задать (см. рис.1):
1. Начало отсчета – произвольную точку O ;
2. Направления трех взаимно перпендикулярных осей
координат, традиционно обозначаемых ( X , Y , Z ) ;
3. Единицу измерения длины (отрезок единичной, по
определению, длины).
Для определения координат точки A необходимо
опустить перпендикуляры из точки A на оси координат
(спроецировать точку на оси координат) и задать
координаты точек-проекций (x, y, z ) . Каждое числокоордината имеет следующий смысл: декартовой координатой точки на прямой
является число, модуль которого равен расстоянию до начала отсчета, а знак
указывает, с какой стороны от начала отсчета находится данная точка.
Так как координата точки указывает расстояние до начала отсчета, то ее
размерность - размерность длины.
Рассмотрим теперь эти известные математические положения с физической точки
зрения.
Пространство, в котором мы живем, не имеет «выделенных» точек и
направлений, с которыми раз и навсегда можно связать единую и абсолютную систему
отсчета. Поэтому положение данного тела можно определить только относительно
других тел. В связи с этим начало отсчета физической системы координат удобно
связывать с некоторым конкретным телом (которое называется тело отсчета).
Направления осей координат также следует связывать с другими материальными телами.
В качестве единицы длины используются эталоны, которые воспроизводятся с помощью
физических приборов. В международной системе единиц СИ единицей длины является
метр.
Подчеркнем, что выбор всех элементов системы координат, в принципе, является
произвольным, следовательно, координаты точки относительны. Иными словами, числакоординаты имеют смысл только в том случае, если задана система координат, то есть
положение данного тела определяется относительно других тел, с которыми связана
система координат.
1
Во многих случаях задание трех координат точки является излишним. Так
если тело движется вдоль заданной (известной) прямой, то имеет смысл одну из осей
(скажем X ) направить вдоль этой прямой. Тогда оставшиеся координаты ( y, x ) все время
будут равны нулю, поэтому их можно не принимать во внимание.
Заметим, что аналогичным образом можно ввести координаты точки на
произвольной заданной линии, измеряя длину участка этой линии между данной точкой и
началом отсчета и указывая с помощью знаков с какой стороны от начала отсчета
находится точка.
Аналогично, при движении тела по заданной плоскости (и даже произвольной
поверхности), достаточно определить в этой плоскости две оси координат.
Эквивалентным координатному является векторный способ описания положения.
В рамках этого метода положение точки в пространстве задается с помощью
r
радиус-вектора r , вектора, соединяющего начало координат с рассматриваемой точкой.
Координатами этого вектора являются декартовые координаты точки (x, y, z ) .
1.2 Преобразования координат.
Как уже было отмечено, координаты точки относительны, они изменяются при
переходе в другую систему координат. Во многих случаях, требуется перейти из одной
системы координат в другую. Получим формулы таких преобразований для одного
частного случая – сдвига начала отсчета на плоскости.
Пусть на известной плоскости заданы две декартовые
системы координат XOY (которую условно назовем
«исходной») и X ' O ' Y ' (назовем ее «сдвинутой»), оси
которых параллельны (см. рис.2). Обозначим (x 0 , y 0 )
координаты начала отсчета сдвинутой системы в исходной
системе.
Как следует из рис. 2, координаты точки A в
сдвинутой и исходной системах связаны очевидными
соотношениями (прямые)
⎧ x' = x − x0
,
(1)
⎨
⎩ y' = y − y0
обратные:
⎧ x = x'+ x0
.
(2)
⎨
y
y
'
y
=
+
0
⎩
Какую из этих систем считать исходной, а какую
сдвинутой, безразлично – системы полностью
равноправны. Заметьте, что обратные преобразования
могут быть получены заменой (x0 , y 0 ) на (− x0 ,− y 0 ) .
Последняя пара чисел является координатами начала
отсчет исходной системы в сдвинутой.
Эти же преобразования короче могут быть записаны и в
векторной форме (рис. 3)
r r r
r r r
(3)
r ' = r − r0 ;
r = r '−r0 .
Аналогичные преобразования при параллельном сдвиге начала отсчета могут быть
получены и в трехмерном случае. Более сложный вид имеют формулы преобразования
координат при повороте осей (в нашем изложении они нам не понадобятся, поэтому
приводить их не будем). Важно, что в любом случае можно найти формулы, позволяющие
2
переходить из одной системы координат в другую. Это обстоятельство, указывает, что
произвол в выборе системы координат не вносит существенных трудностей в описание
движения тел.
1.3 Относительные и инвариантные величины.
Мы показали, что при переходе из одной системы в другую координаты точки
изменяются (координаты относительны). Помимо относительных величин (зависящих от
системы координат) имеются величины независящие от системы координат (такие
величины называются инвариантными). Примером
такой величины является расстояние между двумя
точками. Действительно, пусть на плоскости (рис.4)
расположены две точки: A1 с координатами (x1 , y1 ) и
A2 с координатами (x 2 , y 2 ) . Тогда на основании
теоремы Пифагора расстояние между точками может
быть вычислено по формуле
(4)
s = ( x2 − x1 ) 2 + ( y2 − y1 ) 2 .
При переходе в любую другую систему отсчета (при
неизменной единице длины) расстояние, вычисленное
по формуле (4), остается неизменным. Например, при
сдвиге начала отсчета, описываемом уравнениями (1), все четыре координаты изменятся,
но разности одноименных координат, а, следовательно, и расстояние s останутся
неизменными (инвариантными). Можно указать и другие геометрические инвариантные
величины – углы между отрезками, площади и объемы фигур и др. Особенно отметим, что
соотношения, записанные в векторной форме, остаются неизменными при
преобразованиях координат. Так, например, скалярное произведение1 двух векторов не
зависит от выбора системы координат. В частном случае, скалярное произведение вектора
на самого себя равно квадрату длины вектора. Поэтому формула (4) в векторной форме
имеет вид
r r r r
s = (r1 − r2 ) ⋅ (r1 − r2 ) .
(4а)
Поиск инвариантных величин, не изменяющихся при преобразованиях координат,
представляет большой интерес, а многие физические теории и формулируются в терминах
инвариантных величин.
Задание для самостоятельной работы
1. В полярной системе координат положение точки A на плоскости задается с помощью
а) расстояния r до начала координат O , б) угла ϕ , который образует отрезок OA с
осью X .
Установите связь между полярными (r , ϕ ) и декартовыми координатами точки.
Выразите расстояние между двумя точками через их полярные координаты.
Обсуждая вопрос
умолчали о том, что
геометрических точках
геометрические размеры
об описании положения тела в пространстве, мы стыдливо
не определили понятия «тело». Фактически речь шла о
пространства. Любой реальный объект имеет конечные
и определенную форму. Кроме того, реальные тела обладают
r
r
A и B называется число c , равное
r r
r
произведению модулей векторов на косинус угла α между ними: c = A ⋅ B = A ⋅ B cos α .
1
Напомним, результатом скалярного произведения двух векторов
3
множеством иных характеристик - массой, температурой, цветом и так далее. Полностью
описать все свойства реальных тел, все физические процессы в рассматриваемых телах
невозможно из-за их бесконечного многообразия. Поэтому, рассматривая те или иные
явления необходимо отвлечься, «забыть» на время, пренебречь некоторыми
характеристиками тел и явлений, иными словами, построить модель явления, модель
тела. Какими свойствами тела можно в данных условиях пренебречь зависит от
конкретной физической задачи, конкретной цели физического исследования.
1.4 Материальная точка.
Во многих кинематических задачах оказывается возможным пренебречь размерами
самого тела. Еще раз рассмотрим автомобиль, движущийся из Минска в Брест. Расстояние
между этими городами порядка 350 километров, размеры автомобиля - несколько метров,
поэтому в такой ситуации при описании положения автомобиля можно не учитывать его
размеры - если капот автомобиля находится в Бресте у нужного подъезда нужного дома,
то можно считать, что и его багажник находится приблизительно там же. Таким образом,
в данной задаче можно мысленно заменить автомобиль его моделью - телом, размеры
которого пренебрежимо малы. Такая модель тела очень часто используется в физике и
называется материальной точкой.
Материальная точка - это идеальная модель тела, размерами которого в
данных условиях можно пренебречь.
Общим у геометрической и материальной точек является отсутствие собственных
размеров. Материальную точку, по мере необходимости, можно «наделять» свойствами,
которыми обладают реальные тела, например, массой, энергией, электрическим зарядом и
так далее.
Одним из критериев применимости модели материальной точки является малость
размеров тела по сравнению с расстоянием, на которое оно перемещается. Однако это
условие не является абсолютно однозначным. Так, описывая движение Земли вокруг
Солнца при расчете ее положения на орбите, размерами Земли можно пренебречь, считать
ее материальной точкой. Однако, если нам необходимо рассчитать времена восхода и
заката Солнца, модель материальной точки принципиально неприменима, так как это
описание требует учета вращения Земли, учета ее размеров и формы.
Рассмотрим еще один пример. Спринтеры соревнуются на стометровой дистанции.
Цель описания движения – выявить, кто из спортсменов пробегает дистанцию за меньшее
время (задача чисто кинематическая). Можно ли в данной задаче считать бегуна
материальной точкой? Его размеры значительно меньше дистанции забега, но достаточно
ли они малы, чтобы ими можно было пренебречь? Ответ на эти вопросы зависит от
требуемой точности описания. Так, на серьезных соревнованиях время измеряется с
точностью 0.01 секунды, за это время бегун смещается на расстояние порядка 10
сантиметров (простая оценка, полученная исходя из средней скорости спринтера 10м/с).
Следовательно, погрешность, с которой определяется положением бегуна (10 см) меньше,
чем его поперечные размеры, поэтому модель материальной точки в данном случае
неприменима. Не случайно мастера спринтерского бега на финише «бросают грудь
вперед», выигрывая драгоценные сотые доли секунды. Таким образом, вторым критерием
применимости модели является требуемая точность описания физического явления.
В некоторых ситуациях можно использовать модель материальной точки, даже
если размеры тела сравнимы и даже больше расстояний, на которое смещается тело. Это
допустимо тогда, когда положение одной точки тела однозначно определяет положение
всего тела. Так при скольжении бруска по наклонной плоскости, зная положение его
центра (как, впрочем, и любой другой точки) можно найти положение всего тела. Если
модель материальной точки оказывается неприменимой, то необходимо использовать
другие более сложные модели.
4
1.5 Абсолютно твердое тело.
Многие реальные тела являются твердыми, то есть в течении длительного времени
сохраняют свои размеры и форму, точнее говоря изменения размеров и формы настолько
незначительны, что ими можно пренебречь. Моделью таких тел служит абсолютно
твердое тело.
Абсолютно твердое тело - это идеальная модель тела, изменением размеров и
формы которого в данных условиях можно пренебречь.
Из этого определения следует, что расстояния между двумя любыми точками
абсолютно твердого тела остается неизменным. Абсолютно твердое тело можно также
рассматривать как совокупность материальных точек, жестко связанных между собой. Так
положение океанского лайнера в открытом море можно описать, пользуясь моделью
материальной точки, а его пространственную ориентацию (курс, наклон) с помощью
модели абсолютно твердого тела. Применимость модели абсолютно твердого тела
обусловлена только конкретной исследуемой проблемой - целью моделирования и
требуемой точностью.
1.6 Число степеней свободы тела.
Теперь, после того как мы изучили несколько моделей тел, можно окончательно и
корректно сформулировать ответ на вопрос: «Что означает задать, определить положение
тела?» - Указать численной значение координат некоторых точек тела так, чтобы
положение всего тела (любой его части) было определено однозначно.
Число независимых координат, которые однозначно определяют положение
тела или системы тел в пространстве называется числом степеней свободы.
Число степеней свободы очень важная характеристика описываемой системы, хотя
бы потому, что определяет число независимых уравнений, описывающих движение
системы.
Подсчитаем число степеней свободы некоторых простых систем.
Материальная точка, по определению, не имеет размеров, поэтому ее положение в
пространстве определяется однозначно тремя координатами. Следовательно, число
степеней свободы свободно материальной точки равно трем. Если на движение
материальной точки накладываются дополнительные условия, то число ее степеней
свободы может уменьшиться. Так если точка движется по заданной поверхности, то ее
положение определяется двумя независимыми координатами, следовательно, число
степеней свободы равно двум; при движении по заданной линии число степеней свободы
уменьшается до одной. Подчеркнем, это не значит, что при движении по заданной линии
может изменяться только одна и - могут изменяться все три, но положение точки на
заданной линии определяется одной координатой, и если она известна, то могут быть
определены и две других. Тем не менее, описание положения точки на заданной линии с
помощью одной координаты оказывается не всегда удобным. Ценность рассмотренных
нами декартовых координат в том, что они позволяют установить физические законы,
описывающее движение вдоль всех прямых (все прямые одинаковы!). В то же время, для
описания изменения координат на произвольной линии пришлось бы записывать свои
законы для каждой линии - окружности, параболы, синусоиды и т.д. Поэтому часто
одномерное движение вдоль известной линии описывают с помощью двух или трех
координат. Однако и в этом случае число степеней свободы остается равным единице.
Если механическая система может быть промоделирована как N материальных
точек, движущихся в пространстве, то, очевидно, полное число ее степеней свободы
равняется 3 N . Но если на движение этих материальных точек накладываются
дополнительные ограничения, то число степеней свободы уменьшается.
5
Рассмотрим, как можно описать положение в пространстве двух материальных
точек жестко связанных между собой (что-то похожее на гантели). Две точки имеют
шесть степеней свободы, которые могут быть описаны шестью координатами x1 , y1 , z1 , x2 , y 2 , z 2 , но так как расстояние между точками неизменно, то на эти координаты
накладывается условие
( x1 − x2 ) 2 + ( y1 − y2 ) 2 + ( z1 − z 2 ) 2 = l 2 ,
где l - расстояние между точками, поэтому число независимых координат, или число
степеней свободы равно пяти.
Таким образом, число степеней свободы системы, состоящей из N материальных
точек равно 3 N минус число дополнительных условий (связей), накладываемых на
движение этих точек.
Число степеней свободы может быть подсчитано и другим способом. Обратим
внимание, что точное определение координат уменьшает «подвижность» точки (или
системы точек). Так, например, если для материальной точки задана координата z , то
точка может двигаться только в плоскости перпендикулярной оси Z , задание еще одно
координаты (скажем y ), приводит к тому, что точка может двигаться только вдоль
Поэтому число степеней свободы можно находить,
прямой параллельной оси X .
подсчитывая, сколько независимых координат необходимо определить, чтобы жестко
«закрепить» тело. С помощью такого подхода найдем число степеней свободы системы,
состоящей из двух жестко связанных точек. Задавая три координаты одной точки, мы ее
как бы закрепляем, тогда вторая точка сможет двигаться так, что бы ее расстояние до
первой оставалось неизменным, то есть по поверхности сферы радиуса l . Понятно, что
если определено положение двух точек твердого тонкого стержня, то задано и положение
всего стержня, поэтому тонкий стержень имеет пять степеней свободы.
Посчитаем
число
степеней
свободы
свободно
движущегося абсолютно твердого тела. Выберем внутри тела
три произвольных точки A , B , C , не лежащих на одной прямой.
(рис 5). Положение одной точки A , определяется тремя
координатами, если задано положение точки A , то положение
точки B может быть описано двумя координатами. Наконец,
при «закрепленных» точках A и B , тело может только
вращаться вокруг оси, проходящей через эти точки.
Следовательно, точка C имеет одну степень свободы. Таким
образом, абсолютно твердое тело имеет шесть степеней
свободы.
Как мы уже отмечали, для описания положения точки можно использовать разные
системы координат, аналогично, положение твердого тела также может быть описано
различными способами, только число независимых координат во всех способах описания
будет одним и тем же равным числу степеней свободы. Так во многих случаях, положение
твердого тела, описывают, задавая три декартовые координаты одной из его точек (чаще
центра), и три угла, определяющие его ориентацию.
1.7 Существует ли четвертое измерение?
В научно-фантастических произведения иногда встречаются сюжеты, в которых разумные существа
осваивают четвертое, пятое и так далее измерения2. Повышение размерности пространства предоставляет
новые богатейшие возможности, как для этих существ, так и для писателей-фантастов. Сравните
двухмерную плоскость и трехмерное пространство! Для того чтобы «выйти» из плоскости в трехмерное
пространство можно предложить следующий метод: из центра окружности необходимо провести
бесконечный луч, который нигде не пересекает окружность, такой луч лежит в третьем измерении. По
аналогии можно предложить «путь в четвертое измерение»: из центра сферы необходимо провести луч,
который нигде не пересекает сферу - вообразили? Еще один способ - провести прямую, которая
2
Для примера можно вспомнить знаменитый роман М.Булгакова «Мастер и Маргарита»
6
перпендикулярна трем взаимно перпендикулярным прямым. Конечно, если вам не удалось представить себе
такой луч или такую прямую, то это еще не является доказательством отсутствия четвертого измерения в
нашем пространстве.
Попытаемся представить, к каким наблюдаемым явлениям могло бы привести наличие
дополнительного измерения. Например, «из четвертого измерения» можно было бы заглянуть внутрь
любого трехмерного тела (как из третьего измерения можно видеть «внутренности» любой плоской
фигуры). Далее, был бы возможен бесследный «уход» и обратное появление в любом другом месте любых
материальных тел (опять же представьте себе, что будет происходить на плоскости, которую пересекает
трехмерное тело). К настоящему времени таких фактов не зафиксировано. Более того, не известно таких
явлений, которые не могли бы быть объяснены с точки зрения пространства трех измерений.
Еще одним доказательством трехмерности пространства, в котором мы обитаем, является ряд
физических законов. Рассмотрим, например, точечный источник, который посылает свет во все стороны
равномерно. Понятно, что энергия, пересекающая поверхность любой сферы, внутри которой находится
источник, должна быть постоянна. Следовательно, интенсивность света (то есть энергия, приходящаяся на
единицу площади) должна убывать обратно пропорционально площади сферы, то есть обратно
пропорционально квадрату расстояния. Если бы свет распространялся и в четвертом измерении, то его
интенсивность убывала бы обратно пропорционально кубу расстояния. Эксперимент однозначно
утверждает, что интенсивность убывает обратно пропорционально квадрату расстояния. Эти и другие факты
утверждают, что наше пространство действительно трехмерно. Таким образом, ответ на вопрос этого
раздела в настоящее время следующий:
Пространство четырех и более измерений является математической абстракцией, можно изучать
свойства геометрических объектов в таких пространствах, при решении целого ряда задач, в том числе
физических бывает полезно их рассматривать в многомерных пространствах, однако, в настоящее время нет
никаких оснований полагать, что реально существует четвертое измерение в том смысле, что реально
существуют некоторые материальные тела вне пространства трех измерений.
Вопросы для самостоятельной работы.
1. Подсчитайте число степеней свободы тонкого стержня, толщиной которого можно
пренебречь.
2. Две материальные точки связаны пружиной. Чему равно число степеней свободы
такой системы?
3. Чему равно число степеней свободы руки человека?
1.8 Механическое движение. Закон движения.
Окружающий нас мир не является застывшим, в нем постоянно происходят
всевозможные изменения - «все течет, все изменяется», и нет необходимости убеждать
кого-либо в этой очевидной истине. Простейшим видом изменений, происходящих в
окружающем нас мире, является изменение положений тел в пространстве, механическое
движение.
Механическим движением называется изменение положений тел в
пространстве с течением времени.
При движении материальной точки она описывает в пространстве некоторую
линию. Для описания движения можно попытаться найти эту линию, а затем описывать
положение точки на этой ней. Для этого можно, например, задать зависимость
пройденного пути от времени движения.
Линия, вдоль которой движется материальная точка, называется траекторией
движения.
Путь, пройденный точкой равен длине участка траектории между двумя
последовательными положениями тела.
Однако определение траектории движения часто представляет собой отдельную и
достаточно сложную задачу, поэтому часто оказывается более простым и удобным
описывать механическое движение иным способом.
Мы уже знаем, что положение тела в пространстве описывается с помощью
координат. Если положение тела изменяется, то изменяются и его координаты, они
становятся зависящими от времени, становятся функциями времени.
7
Зависимость всех координат тела от времени называется законом движения.
Таким образом, закон движения определяет положение тела в любой произвольный
момент времени. Математическим выражением закона движения является набор функций
- зависимостей координат от времени. Таким образом, нам необходимо дополнить
рассмотренную систему координат прибором для измерения времени - часами. Дальше
такой набор - системы координат и часов мы будем называть системой отсчета. Как
всякая функция закон движения может быть представлен в нескольких формах - в виде
таблицы, в виде графика, в виде формулы.
Подчеркнем, что закон движения полностью описывает движение, дает
исчерпывающую информацию о движении, зная его можно найти любую характеристику
движения. Однако, задача физики, заключается не только в том чтобы просто описать
наблюдаемое движение, более важная задача - научиться предсказывать движение,
рассчитывать его, строить его модели, создавать условия, для того чтобы получить
движение требуемого вида. Для успешного решения таких проблем нам необходимо
ввести и изучить некоторые характеристики механического движения (скорость,
ускорение и т.д.), которые позволяют теоретически находить законы движения.
8
§2 Кинематическое описание механического движения материальной точки.
2.1 Скорость материальной точки при равномерном движении по прямой.
Пусть некоторое тело, которое можно считать материальной точкой, движется
вдоль заданной прямой. Для описания его движения направим ось X декартовой системы
координат вдоль этой прямой (которая является траекторией движения), выберем также на
этой оси начало отсчета. Положение тела однозначно определяется одной координатой,
поэтому закон движения в данном случае представляет собой одну функцию зависимость
координаты x от времени t - x(t ) . Рассмотрим наиболее простой вид движения равномерное.
Равномерным называется такое движение точки, при котором за любые
равные промежутки времени она проходит равные пути.
При таком движении легко определить физическую характеристику быстроты
движения - скорость.
Скоростью равномерного движения называется отношение пути, пройденного
телом, к интервалу времени, за который этот путь пройден. Эту величину также
называют путевой скоростью.
Если обозначить пройденный путь S , а интервал времени t , то скорость v , как
вам известно, определяется формулой
S
(1)
v= .
t
При равномерном движении это отношение не зависит от рассматриваемого промежутка
времени, так как пройденный путь пропорционален временному интервалу. Можно дать
еще одно истолкование скорости - скорость тела равна пути, пройденному телом за
единицу времени.
Скорость - есть физическая величина, имеющая в системе СИ размерность м/с
(метр в секунду). Кроме этой единицы измерения скорости довольно часто используется
внесистемная единица - км/час, а в некоторых странах миль/час.
Величина пройденного пути S показывает, на сколько сместилось тело, но не
указывает направление этого смещения. Используя введенные координаты, можно
определить смещение тела как изменение его координаты 1
∆x = x − x 0 ,
(2)
где x - координата тела в некоторый момент времени t , а x0 - координата тела в
начальный момент t 0 . Изменение координаты может быть как положительным (при
увеличении значения координаты), так и отрицательным (при ее уменьшении). Таким
образом, знак величины ∆x просто указывает направление движения, в положительном,
либо отрицательном направлении оси X . Очевидно, что путь, пройденный материальной
точкой при движении вдоль оси в одном направлении, связан с изменением координаты
соотношением
S = ∆x .
(3)
Соответствующим образом можно переопределить и скорость движения - скорость
равномерного движения вдоль прямой равна отношению изменения координаты к
промежутку времени, в течение которого это изменения произошло x − x 0 ∆x
v=
.
(4)
=
t − t0
∆t
Символом ∆ (греческая буква «дельта») мы будем обозначать изменение любой физической величины (в
данном случае координаты) - конечное значение минус начальное; такое обозначение является
общепринятым.
1
9
Заметьте, для величины интервала времени мы также используем обозначение ∆t разность между показаниями часов в конечный и начальный момент времени. В данном
определении скорость может быть положительной (если тело движется в положительном
направлении оси) и отрицательной (при движении в противоположном направлении).
Таким образом, знак скорости указывает направление движения, а ее модуль
сохраняет прежнее значение - путь, пройденный в единицу времени.
2.2. Средняя и мгновенная скорость при движении точки по прямой.
Как мы уже отмечали, равномерное движение является простейшей моделью
механического движения. Если такая модель неприменима, то необходимо использовать
более сложные модели. Для их построение нам необходимо рассмотреть понятие скорости
в случае неравномерного движения.
Пусть за интервал времени от t 0 до t1 координата точки изменилась от x0 до x1 . Если мы
вычислим скорость по прежнему правилу
∆x x1 − x0
vcp. =
=
,
(1)
∆t
t1 − t 0
то получим величину (она называется средней скоростью), которая описывает быстроту
движения «в среднем» - вполне возможно, что за первую половину времени движения
точка сместилась на большее расстояние, чем за вторую.
Средней скоростью называется физическая величина равная отношению
изменения координаты точки к интервалу времени, в течение которого это
изменение произошло.
Геометрический смысл средней скорости - коэффициент наклона секущей AB
графика закона движения.
Для более детального, более точного описания движения, можно задать два
значения средней скорости – за первую половину времени движения vcp.1 , за вторую
половину - vcp.2 .Если и такая точность нас не устраивает - то необходимо дробить
временные интервалы дальше - на четыре, восемь и т.д. частей. При этом необходимо
задавать соответственно четыре, восемь и т.д. значений средних скоростей. Согласитесь,
такое описание становится громоздким и неудобным. Выход из этой ситуации давно
найден - он заключается в том, что бы рассматривать скорость как функцию времени.
Давайте посмотрим, как будет меняться средняя скорость при уменьшении
промежутка времени, за который мы эту скорость вычисляем. На рис.6 показан график
зависимости координаты материальной точки от времени. Будем вычислять среднюю
скорость за интервал времени от t 0 до t1 , последовательно приближая значение t1 к t 0 .
При этом семейство секущих A0 A1 , A0 A1 , A0 A1′ , A0 A1′′ (рис.6), будет стремиться к
10
некоторому предельному положению прямой A0 B , которая является касательной к
графику закона движения. Мы приводим два различных случая, чтобы показать, что
мгновенная скорость может быть как больше, так и меньше средней скорости. Эту
процедуру можно описать и алгебраически, последовательно вычисляя отношения
x − x0
x ′ − x0
x′′ − x0
′.= 1
′′ . = 1
vcp. = 1
, vcp
, vcp
. При этом оказывается, что эти величины
t1 − t 0
t1′ − t 0
t1′′ − t 0
приближаются к некоторому вполне определенному значению. Это предельное значение
получило название мгновенной скорости.
Мгновенной скоростью называется отношение изменения координаты точки
к интервалу времени, за которое это изменение произошло, при интервале времени,
стремящемся к нулю2:
∆x
(2)
v=
, при ∆t → 0 .
∆t
Геометрический смысл мгновенной скорости - коэффициент наклона касательной к
графику закона движения.
Таким образом, мы «привязали» значение мгновенной скорости к конкретному
моменту времени - задали значение скорости в данный момент времени, в данной точке
пространства. Тем самым у нас появилась возможность рассматривать скорость тела как
функцию времени, или функцию координаты.
С математической точки зрения это гораздо удобней, чем задавать значения средних скоростей на
многих малых временных промежутках. Однако давайте задумаемся, а имеет ли физический смысл скорость
в данный момент времени? Скорость - характеристика движения, в данном случае перемещения тела в
пространстве. Для того чтобы зафиксировать перемещение необходимо наблюдать за движением в течение
некоторого промежутка времени. Чтобы измерить скорость, также необходим промежуток времени. Даже
самые совершенные измерители скорости радарные установки измеряют скорость движущихся автомобилей
пусть за малый (порядка одной миллионной доли секунды) промежуток времени, а не в какой-то момент
времени. Следовательно, выражение «скорость в данный момент времени» с точки зрения физики
некорректно. Тем не менее, в механике постоянно пользуются понятием мгновенной скорости, которое
очень удобно в математических расчетах. Математически, логически мы можем рассмотреть предельный
переход ∆t → 0 , а физически имеется минимально возможное значение промежутка ∆t , за который
можно измерить скорость.
В дальнейшем, говоря о скорости, мы будем иметь в виду именно мгновенную скорость. Заметим,
при равномерном движении мгновенная скорость равна ранее определенной скорости, потому, что при
∆x
не зависит от величины промежутка времени, поэтому остается
∆t
неизменным и при сколь угодно малом ∆t .
Так как скорость может зависеть от времени, то ее следует рассматривать как
функцию времени, и изображать ее в виде графика.
равномерном движении отношение
2.3 Ускорение при движении точки по прямой.
После того, как мы разобрались с понятием мгновенной скорости («скорости в
данный момент времени»), у нас появилась возможность говорить об изменении скорости,
определить физическую величину, описывающую это изменение. Пусть в момент времени
t 0 скорость точки была v0 , а в момент времени t1 > t 0 стала равной v1 . Тогда отношение
изменения скорости к промежутку времени, в течение которого это изменение
произошло, называется ускорением точки
2
В высшей математике это определение записывают с помощью специального символа
∆x
, кроме того, процедура вычисления подобного предела называется
∆t →0 ∆t
lim (предел - limit): v = lim
взятием производной.
11
v1 − v0 ∆v
=
.
(1)
t1 − t 0
∆t
Можно сказать, что ускорение - это скорость изменения скорости тела.
Ускорение физическая величина, размерность которой есть отношение
размерности скорости к размерности времени, поэтому в системе СИ размерность
[v] = ( м / с) = м - «метр разделить на секунду в квадрате» или «метр в
ускорения [a ] =
[t ]
с
с2
секунду за секунду».
Обсуждая данное определение, мы должны повторить все наши рассуждения,
касающиеся перехода от понятия средней к понятию мгновенной скорости. Так возможны
∆v
ситуации, когда отношение
не зависит от величины интервала ∆t - в этом случае
∆t
ускорение является постоянной величиной, и такое движение называется
∆v
равноускоренным. Если же величина
зависит от промежутка времени, то формула
∆t
(1) дает значение среднего ускорения на интервале времени от t 0 до t1 . Для более
детального описания движения необходимо рассмотреть предельный переход к малому
∆v
промежутку времени, тогда предельное значение отношения
будет являться
∆t
мгновенным ускорением, или ускорением «в данный момент времени».
Заметим, что ускорение, как и скорость, может быть как положительным, так и
отрицательным. Напомним, что знак скорости указывает направление движения. Смысл
знака ускорения иной - он показывает направление изменения скорости.
Рассмотрим теперь геометрический смысл
мгновенного ускорения. Для этого построим график
зависимости скорости от времени для некоторой
движущейся точки (на рис. 7 - плавная кривая A0 A1 ).
Пусть в момент времени t 0 скорость тела равна v0
(точка A0 на графике), а в момент времени t1 - скорость
v1 (точка A1 на графике). В прямоугольном треугольнике
A1C ∆v
A0 A1C отношение длин катетов
(то есть
=
A0 C ∆t
среднее ускорение)
численно равно тангенсу угла
наклона секущей A0 A1 к оси времени. При уменьшении интервала времени (то есть при
t1 → t 0 ) секущая A0 A1 стремится к касательной A0 B . Следовательно, тангенс угла наклона
касательной к графику зависимости скорости от времени численно равен мгновенному
ускорению.
a=
Обязательно следует отметить, что к выражению «тангенс угла наклона» (как и в случае скорости) необходимо
относится с физической, а не с геометрической точки зрения - длины рассматриваемых катетов являются физическими
величинами, имеющими различную размерность, поэтому и «тангенс» имеет размерность - в данном случае ускорения. Поэтому в дальнейшем мы будем использовать термин коэффициент наклона касательной к оси времени.
При равномерном движении с постоянной скоростью
v0 график зависимости скорости от времени является
прямой линией, параллельной оси времени (на рис.8 прямая AB ). Рассмотрим промежуток времени от t 0 до t1 .
Произведение величины этого интервала (t1 − t 0 ) на
скорость v0 равно, с одной стороны изменению координаты
12
∆x , а с другой площади прямоугольника под графиком зависимости скорости от времени.
Площадь под графиком следует понимать опять же таки в физическом смысле - как произведение
физических величин, имеющих различную размерность, а не в чисто геометрическом смысле - как
произведение длин отрезков.
Площадь под графиком зависимости скорости от времени равна изменению
координаты при любой зависимости скорости от времени v(t ) . Для доказательства этого
утверждения достаточно разбить время движения на малые
интервалы, в течение которых движение можно считать
равномерным.
Дополним наше определение площади под кривой еще
одной договоренностью - будем считать, что если кривая лежит
под осью времени (то есть скорость отрицательна), то и
соответствующую площадь будем считать отрицательной (см.
рис. 9).
В случае произвольного движения ускорение также может изменяться в процессе
движения. Таким образом, можно говорить о зависимости ускорения от времени (или от
координаты) и представлять эту зависимость графически. Рассматривая график
зависимости ускорения от времени, можно показать, что площадь под графиком этой
зависимости численно равна изменению скорости точки (доказательство аналогично
рассмотрению зависимости скорости от времени).
2.4 Кинематические характеристики движения материальной точки в трехмерном
пространстве.
Положение материально точки в пространстве описывается тремя координатами.
Если положение точки изменяется с течением времени, то ее координаты становятся
функциями времени. Закон движения в таком случае задается тремя функциями зависимостями трех координат от времени
⎧ x = x(t )
⎪
(1)
⎨ y = y (t ) .
⎪ z = z (t )
⎩
Система функций (1) полностью определяет движение материальной точки, то есть
позволяет найти ее положение в произвольный момент времени. Основное отличие
движения в пространстве от движения вдоль заданной прямой заключается в наличии трех
координат. Поэтому следует говорить от трех скоростях, трех ускорениях, которые
определяются полностью аналогично одномерному случаю.
Так вместо скорости движения вдоль оси, можно (и нужно) определить три
скорости движения вдоль трех осей, вместо ускорения - три ускорения вдоль трех осей
∆v
⎧
∆x
⎧
ax = x
v
=
⎪
x
⎪
∆t
∆t
⎪
⎪
∆v y
∆y
⎪
⎪
;
.
(2)
⎨a y =
⎨v y =
t
∆
t
∆
⎪
⎪
∆v z
∆z
⎪
⎪
⎪a z = ∆t
⎪v z = ∆t
⎩
⎩
Координатный способ описания движения является универсальным. Однако он
имеет несколько существенных недостатков. Прежде всего, он очень громоздкий - требует
написания большого числа однотипных формул, часто отличающихся только индексами
(подобно уравнениям (2)). Еще более существенным недостатком этого метода является
необходимость «привязываться» к конкретной системе отсчета. Поэтому в кинематике (да
и во всей физике) часто используется векторный метод описания механического движения
(и других физических явлений).
13
2.5 Векторные характеристики движения материальной точки.
Положение точки в пространстве можно задать с помощью вектора,
соединяющего начало координат с данной точкой - rтакой вектор называется радиусвектором точки, мы будем обозначать его символом r . Очевидно, что координаты этого
вектора, совпадают с координатами точки ( x, y, z ) , поэтому мы оставим эти обозначения и
для координат радиус-вектора.
Если тело изменяет свое положение в пространстве, то его радиус-вектор будет
изменяться с течением времени, то есть станет функцией времени. Зависимость радиусr
вектора от времени r (t ) будет являться законом движения.
Изменение положения в векторной форме
удобно
описывать
с
помощью
вектора
r
перемещения S - вектора, соединяющего
r
r
начальное r0 и конечное положение r1
движущейся точки. Вектор перемещения равен
разности радиус-векторов конечного и начального
положения (см. рис.10)
r r r
S = r1 − r0 .
(1)
Отношение изменения радиус-вектора к
промежутку времени, за который это изменение
произошло, называется средним вектором
скорости (или просто средней скоростью):
r
r
∆r
.
(2)
Vср. =
∆t
Если промежуток времени, за который измеряется изменения радиус-вектора,
сделать очень малым (предельно малым), то вектор средней скорости перейдет в вектор
мгновенной скорости
r
r ∆r
v=
, при ∆t → 0 .
(3)
∆t
Это определение является наиболее общим определением скорости. Заметим, что при
постоянном векторе скорости тела его траекторией
обязательно является прямая линия.
Выясним, как направлен вектор мгновенной
скорости по отношению к произвольной траектории
движения материальной точки. Пусть тело (которое мы
считаем материальной точкой) переместилось за
промежуток времени ∆t по некоторой траектории из
точки A0 в точку A1 (см. рис.11). Вектор средней скорости совпадает по направлению с
r
вектором перемещения S . При уменьшении рассматриваемого промежутка времени
∆t точка A1 будет находиться все ближе к точке A0 , соответственно, будет изменяться и
вектор перемещения, при ∆t → 0 вектор перемещения будет стремиться к касательной к
траектории, поэтому вектор мгновенной скорости направлен вдоль касательной к
траектории.
r
Вектором ускорения a называется отношение изменения вектора скорости к
промежутку времени, в течение которого это изменение произошло, при стремлении
этого промежутка к нулю:
r
r ∆v
a=
, при ∆t → 0 .
(5)
∆t
Подчеркнем, что в данном определении ускорения фигурирует изменение вектора
скорости - а вектор может изменяться как по величине, так и по направлению.
14
Следовательно, непрямолинейное (криволинейное) движение тела обязательно является
движением с ускорением (так как изменяется направление вектора скорости).
Простейшие модели движения.
Реальные движения реальных тел, как правило, довольно сложны – разгон,
торможения, повороты, скорости, ускорения тел постоянно изменяются. Однако во
многих случаях для описания движения можно использовать достаточно простые
(конечно, приближенные) модели, к рассмотрению которых мы сейчас и приступим.
2.6 Равномерное движение материальной точки вдоль прямой.
Напомним, что равномерным называется движение с постоянной скоростью. Так
как скорость величина векторная, то постоянство скорости предполагает постоянство и
направления движения, то есть движение по прямой линии3. При таком движении можно
совместить направление одной из осей системы координат вдоль траектории движения,
тогда движение материальной точки полностью описывается одной функцией
Найдем зависимость координаты от времени (закон движения) при равномерном
∆x
движении вдоль прямой. Непосредственно из формулы v =
, определяющей скорость
∆t
движения, можно выразить
x = x0 + v(t − t 0 ) .
(1)
Эта формула дает закон движения материальной точки при ее равномерном
движении вдоль прямой. Знание только скорости движения не позволяет однозначно
определить его закон - необходимо знать положение (то есть координату) тела в какой-то
момент времени. Часто это дополнительное условие называют начальным - в начальный
момент времени t 0 тело находится в точке с координатой x0 . Однако, совсем не
обязательно, чтобы движение начиналось в момент времени t 0 - формулу (1) можно
применять для любых времен t (в том числе и t < t 0 ), важно только, чтобы во все
рассматриваемые моменты времени продолжалось движение с той же скоростью. В этом
смысле закон движения обратим - его можно использовать как для того, чтобы
предсказать положение тела в будущем ( t > t 0 ), так и для того, чтобы определить, где оно
находилось в прошлом ( t < t 0 ).
При рассмотрении системы координат мы неоднократно подчеркивали, что выбор
начала отсчета координат произволен, так же произволен и выбор начала отсчета времени
t 0 . Физический смысл этого «произвола» - вы можете пустить свои часы в любой удобный
для вас момент времени. Поэтому часто в формуле закона движения полагают, что
t 0 = 0 , тогда
x = x0 + vt .
(2)
Различие между формулами (1) и (2) при описании одного и того же движении только в
начальном отсчете времени: при описании движения с помощью формулы (1) полагают,
что тело находилось в точке с координатой x0 при t = t 0 , а в формуле (2) при t = 0 .
С математической точки зрения закон движения является функцией, и как всякая
функция может быть проиллюстрирован графиком. Графическое представление
различных законов наглядно, информативно и чрезвычайно распространено как в физике,
так и в других естественных науках.
3
Тем не менее, достаточно часто говоря о равномерном движении, подразумевают постоянство только
модуля, величины скорости. В этом смысле правомочно говорить, например, о равномерном движении по
окружности.
15
Построим
график
функции,
описываемой уравнением (1). Зависимость
x(t ) в данном случае линейна, поэтому ее
график является прямой линией (рис. 12). Эта
прямая проходит через точку 4 A с
координатами (t 0 , x 0 ) . Точки пересечения
графика с осями координат также имеют
наглядный физический смысл:
x1
положение тела в момент времени t = 0 ; t 2 момент времени, когда тело находилось в
точке начала отсчета. Наклон графика определяется скоростью точки - чем выше
скорость, тем больший угол образует график с осью t .
Иногда говорят, что скорость численно равна тангенсу угла наклона графика
закона движения к оси времени. Действительно, в прямоугольном треугольнике АВС
длина отрезка ВС равна ∆t , а длина отрезка АС равна ∆x . Следовательно, их отношение,
с одной стороны равно скорости движения v = ∆x / ∆t , а, с другой - тангенсу угла ∠ABC .
К этому утверждению следует относиться с большой осторожностью, так как изменения
координаты ∆x и времени ∆t являются физическими величинами и имеют разные
размерности, поэтому масштабы соответствующих осей могут выбираться произвольно,
независимо друг от друга. Изменение масштаба одной из осей приведет к изменению угла
наклона графика, скорость же при этом, конечно, не изменится. Поэтому измерять
скорость с помощью транспортира не разумно. Поэтому «тангенс наклона»
∆x / ∆t
следует понимать как отношение физических величин, а не длин отрезков на рисунке с
произвольным масштабом. Во избежание подобной путаницы в дальнейшем для
обозначения отношения ∆x / ∆t мы будем использовать термин - коэффициент наклона
На рис. 13 приведены графики законов движения
нескольких человек вдоль одной прямой, причем их движение
может быть словесно описано следующим образом: «Из пункта A
x A ) одновременно
(расположенного в точке с координатой
вышли два пешехода, причем второй двигался со скоростью в два
раза большей скорости первого. Навстречу им из пункта B
(расположенного в точке с координатой
x B ) вышел третий
пешеход, со скоростью равной скорости второго. Третий пешеход
встретил второго в момент времени t 1 в точке с координатой x1 ,
а затем первого в момент времени t 2 в точке с координатой x 2 ,.
В момент времени t 3 он прибыл пункт A .» Вот такая «история»
изображена на этом графике! Согласитесь, графический способ
описания гораздо короче и нагляднее.
В том случае, когда мы описываем движение нескольких тел в разных
направлениях, неразумно для каждого тела вводить свою систему координат. В такой
ситуации предпочтительнее ввести одну систему координат, а движение каждого тела
описывать в векторной форме.
4
У нас начинают проявляться недостатки разговорного языка: «материальная точка (модель тела)
находится в точке (положение тела в пространстве) с координатой x0 , что соответствует точке А (точка на
рисунке) на графике закона движения». Эти недостатки создают определенные трудности, однако в
большинстве случаев из смысла фразы понятно о каких «точках» и «координатах» идет речь.
16
Непосредственно из определения вектора скорости
r
r ∆r
v=
следует, что векторная
∆t
запись закона равномерного движения имеет вид
r r r
r = r0 + v (t − t 0 ) ,
(3)
r
где r
- радиус-вектор точки в произвольный момент
r
времени t , r0 - радиус-вектор точки в некоторый момент
времени t 0 . По поводу закона движения (3) можно
повторить все рассуждения, касающиеся необходимости
задания начальных условий, приведенные ранее.
Заметим, что уравнение (3), как любое векторное
соотношение, имеет наглядную геометрическую
r
интерпретацию (рис.14), причем величина v (t − t 0 ) также
является вектором и может быть изображена в виде
направленного отрезка A0 A1 .
Мы построили и описали одну из моделей механического движения, которая как
всякая модель упрощает действительное движение. Но эта модель может применяться (и
применяется!) для описания некоторых реальных движений. Необходимо только строго
очертить рамки ее применимости, которые определяются постановкой задачи - насколько
подробно, детально и с какой точностью требуется описать движение. По определению,
движение является равномерным, если за равные промежутки времени тело проходит
равные отрезки пути. Следовательно, движение можно считать (моделировать)
равномерным, если можно пренебречь различиями в расстояниях, проходимых
телом за равные промежутки времени.
2.7 Равноускоренное движение точки по прямой.
Пусть материальная точка движется вдоль заданной прямой линии так, что ее
ускорение остается постоянным. Такое движение точки называется равноускоренным5
или равнопеременным движением. По-прежнему, направим ось X вдоль прямой, по
которой движется точка, и введем обычным образом координаты на этой прямой.
Используя определение ускорения
v − v 0 ∆v
(1)
a=
=
t − t0
∆t
и учитывая, что при постоянном ускорении это отношение не зависит от значения
интервала времени, мы можем выразить значение скорости в произвольный момент
времени t
v = v0 + a(t − t 0 ) .
(2)
Это выражение определяет скорость как функцию времени. Как следует из полученного
уравнения, зная только ускорение, нельзя однозначно определить скорость в
произвольный момент времени. Для этого необходимо задать дополнительное условие:
скорость v0 в некоторый момент времени t 0 . Часто это условие называют начальным и,
полагая t 0 = 0 , называют величину v0 начальной скоростью.
5
Мы будем использовать термин равноускоренное движение в любом случае, когда ускорение постоянно,
независимо от того, увеличивается или уменьшается скорость движения. Поэтому по нашему определению
точка может двигаться равноускоренно, замедляясь. Иногда движение с отрицательным ускорением
называют равнозамедленным, но чтобы избегать лишних сложностей этот термин употреблять не будем.
17
Графиком зависимости скорости от времени
при равноускоренном движении (то есть графиком
функции (2)) является прямая линия, проходящая
через точку A с координатами (t 0 , v0 ) , коэффициент
наклона которой равен ускорению точки (рис.15).
Как было показано ранее площадь под
графиком зависимости скорости от времени равна
изменению координаты точки. Воспользуемся этим
правилом, для того чтобы решить основную задачу
кинематики
- найти закон движения - для
равноускоренного движения. Изменение координаты
∆x в данном случае численно равно площади
трапеции
t0t1 A1 A , которая вычисляется как
произведение полусуммы оснований на высоту
v +v
v + v + a(t1 − t 0 )
⋅ (t1 − t 0 ) =
∆x = 0 1 ⋅ (t1 − t 0 ) = 0 0
2
2
.
(3)
a(t1 − t 0 ) 2
= v0 (t1 − t0 ) +
2
При выводе этого соотношения мы учли, что v1 = v0 + a(t1 − t 0 ) . При равноускоренном
движении полученное соотношение справедливо для любого момента времени t1 ,
поэтому вместо конкретного значения t1 можно подставить переменную величину текущее время. Изменение координаты по определению равно ∆x = x − x0 , следовательно,
закон движения имеет вид
a(t − t 0 ) 2
.
(4)
x = x0 + v0 (t − t 0 ) +
2
В той формуле x0 - координата, а v0 - скорость в момент времени t 0 . Часто эти параметры
называют начальными. Обратите внимание, чтобы найти закон движения при
постоянном ускорении, помимо значения ускорения необходимо задать два
дополнительных условия - координату и скорость в некоторый момент времени. Закон
движения (4) можно использовать не только для t > t 0 , но и для любые других моментов
времени, если конечно вы уверены, что в эти моменты характер движения не изменялся.
v −v
Вернемся к цепочке преобразований (3). Из уравнения (2) следует t1 − t 0 = 1 0 .
a
Подставим это выражение в формулу (3)
v +v
v +v v −v
v 2 − v02
∆x = 0 1 ⋅ (t1 − t 0 ) = 0 1 ⋅ 1 0 = 1
.
(5)
2
2
a
2a
Мы получили важное соотношение, позволяющее найти изменение координаты тела по
известным ускорению, начальной и конечной скоростям. Так, например, тормозной путь
автомобиля S может быть легко подсчитан по этой формуле: полагая конечную скорость
равной нулю и, учитывая, что при торможении ускорение отрицательно a = − a , из
v02
.
2a
Рассмотрим подробнее характер движения при различных значениях параметров
равноускоренного движения. Выбор начала отсчета времени, как и выбор начала отсчета
формулы (5) следует, что S =
18
координаты произволен, поэтому при изучении движения одного тела, мы можем
положить6 t 0 = 0 и x0 = 0 . Таким образом рассмотрим закон движения в форме
at 2
.
(4)
2
При этом скорость тела изменяется по закону
(5)
v = v0 + at .
Удобно одновременно исследовать обе функции - зависимости от времени
скорости и координаты. С графиками функции (5) мы уже познакомились - это прямые
линии. В общем случае координата зависит от времени по квадратичному закону, поэтому
графиком этой функции является парабола.
Рассмотрим несколько частных случаев.
1. Начальная скорость v0 = 0 . В этом случае исследуемые функции имеют вид
x = v0 t +
v = at ,
x=
at 2
.
2
Прямые зависимостей v(t ) проходят через начало координат, вершины парабол
зависимостей x(t ) совпадают с началом координат (естественно, своих). Увеличение
ускорения приводит к увеличению коэффициента наклона прямой v(t ) , и увеличению
крутизны парабол x(t ) . При отрицательном значении ускорения наклон прямых v(t )
становится отрицательным, а ветви парабол x(t ) опускаются вниз.
На
рис.16
показаны
описанные
зависимости
для
значений
ускорения
2
2
2
0,5 м / с , 1,0 м / с , 1,5 м / с (графики
1,2,3)
и
отрицательных
2
2
2
ускорений − 0,5 м / с , −1,0 м / с , −1,5 м / с (графики 4,5,6).
2. Положительное ускорение a > 0 , начальная скорость отлична от нуля v0 ≠ 0 .
График зависимости скорости от времени имеет вид прямой (рис.19). Значение начальной
скорости равно длине отрезка, который отсекает график на оси скорости. График
зависимости координаты от времени является параболой, ветви которой направлены
вверх, проходящей через начало координат. Проведем касательную к этой параболе в
начальной точке. Как мы показали ранее, коэффициент наклона касательной равен
6
Если же мы рассматриваем одновременно движение нескольких тел, то мы можем выбрать только
одно начало отсчета, общее для всех рассматриваемых тел, поэтому добиться того, чтобы x0 = 0 для всех
тел, не возможно (за исключением того случая, когда все тела стартуют из одной точки).
19
мгновенной скорости. В момент времени t = 0 коэффициент наклона касательной,
следовательно, совпадает с начальной скоростью v0 . Если начальная скорость
положительна, то парабола стремится вверх.
Рассмотрим теперь случай, когда ускорение осталось прежним a > 0 , но начальная
скорость отрицательна vo < 0 . В этом случае прямая зависимости v(t ) «стартует» с
отрицательных значений скорости. Поэтому касательная к параболе зависимости x(t ) в
начальный момент имеет отрицательный наклон, хотя ветви параболы по-прежнему
направлены вверх. До тех пор пока скорость отрицательна, координата убывает, достигая
минимального значения в момент времени, когда скорость становится равной нулю. Это и
понятно и с точки зрения здравого смысла: пока скорость отрицательна, точка движется
в отрицательном направлении оси, как только скорость становится положительной, точка
начинает двигаться в противоположном направлении, следовательно, в момент времени,,
когда v = 0 , точка находилась на максимальном удалении от начала отсчета. Это
утверждение является универсальным правилом - если скорость точки изменяет знак,
то в момент времени, когда скорость равна нулю, точка находится в своем крайнем
положении (координата минимальна или максимальна).
Посмотрите, как изменяются графики зависимостей скорости и координаты при
изменении начальной скорости. На рис. 17 построены зависимости v(t ) и x(t ) при
одинаковом ускорении a = 1,0 м / с 2 , но при разных начальных скоростях. Заметьте, что
прямые v(t ) параллельны, а все параболы x(t ) одинаковы - они отличаются только
положением вершины.
Другие комбинации начальных параметров можно рассмотреть аналогично - в
частности, случай a < 0, v0 ≠ 0 является зеркальным отражением только что
рассмотренной ситуации - его можно свести к рассмотренному варианту, просто изменив
направление оси X .
Итак, мы рассмотрели еще одну модель - равноускоренное движение. Надо
отметить, что движение, близкое к равноускоренному, довольно часто встречается в
окружающем нас мире. Так, если тело движется под действием постоянных сил, то его
движение является равноускоренным. Например, свободное падение массивных тел,
скатывание шара с наклонной плоскости - примеры такого движения.
Тем не менее, модель равноускоренного движения также является приближенной.
Если в названных примерах сопротивление воздуха играет существенную роль, то
20
ускорение тел будет заметно изменяться, поэтому модель равноускоренного движения
окажется неприменимой.
2.8 Равноускоренное движение в пространстве.
Полученные выражения для законов равномерного и равноускоренного движения
легко обобщаются на случай движения материальной точки в трехмерном пространстве.
Положение материальной точки в пространстве описывается либо с помощью трех
координат (x, y, z ) , либо эквивалентным векторным способом посредством задания
r
радиус-вектора точки r . При движении эти величины становятся функциями времени.
Следовательно, механическое движение материальной точки в общем случае полностью
описывается заданием трех функций (x(t ), y (t ), z (t )) , или одной эквивалентной векторной
r
функции r (t ) . В случае равноускоренного движения7 вид зависимости скорости от
r
времени V (t ) непосредственно следует из определения вектора ускорения
r
r r
V (t ) = V0 + at ,
(1)
r
здесь V0 - вектор скорости в момент времени t = 0 . Формула (1) является обобщением
полученного ранее выражения для скорости при движении вдоль прямой. Векторная
запись функции (1) эквивалентна развернутой «координатной» записи
⎧V x = V x 0 + a x t
⎪
(1а)
⎨V y = V y 0 + a y t ,
⎪
⎩V z = V z 0 + a z t
r r
где V x 0 ,V y 0 ,V z 0 и a x , a y , a z - проекции векторов V0 , a на соответствующие оси координат.
Аналогично можно обобщить зависимость координат материальной точки от времени при
равноускоренном движении
r
r
r r
at 2
,
(2)
r (t ) = r0 + V0 t +
2
r
здесь r0 - радиус-вектор точки в момент времени t = 0 . Соотношение (2) также можно
переписать в координатной форме
⎧
axt 2
⎪ x = x0 + V x 0 t +
2
⎪
⎪⎪
ayt 2
,
(2а)
=
+
+
y
y
V
t
⎨
y0
0
2
⎪
⎪
azt 2
z
z
V
t
=
+
+
⎪
z0
0
2
⎪⎩
где (x 0 , y 0 , z 0 ) - координаты точки в момент времени t = 0 . Мы не будем отдельно изучать
равномерное движение, так как сейчас его можно рассматривать как частный случай
движения равноускоренного, но с нулевым ускорением.
В качестве широко известного примера равноускоренного движения рассмотрим
движения небольшого тела (которое мы будем считать материальной точкой) в поле
тяжести земли, без учета сопротивления воздуха.
7
По прежнему, равноускоренным движением мы называем движение с постоянным ускорением, в данном
r
случае вектором ускорения a .
21
Как известно, в этом случае тело движется с постоянным ускорением свободного
r
падения g , направленным вертикально вниз. Пусть небольшое тело брошено с начальной
r
скоростью V0 , направленной под углом α к горизонту, вдоль горизонтальной
поверхности. Совместим начало отсчета с точкой бросания.
В этом случае в векторной форме закон движения тела записывается в виде
r
r r
gt 2
.
(3)
r = V0 t +
2
Векторная форма записи допускает наглядную геометрическую интерпретацию (Рис.18):
r
радиус-вектор тела r (отрезок ОВ) в произвольный момент времени t равен сумме
r
r
gt 2
(отрезок АВ). При желании можно воспользоваться
векторов V0 t (отрезок ОА) и
2
геометрическими соотношениями для определения любых характеристик движения.
Например, для определения дальности S полета можно записать соотношения между
сторонами прямоугольного треугольника OA1B1 :
S = V0 t1 cos α
,
gt12
= V0 t1 sin α
2
из которых без труда можно выразить как дальность полета, так и время движения t1 :
t1 =
2V0 sin α
g
.
2V02 sin α cos α
S=
g
Более простым и распространенным способом
кинематического описания является координатный.
Продемонстрируем преимущества этого метода на
примере рассматриваемой задачи. Для этого введем
систему декартовых координат, ось X
которой
направим горизонтально, а ось Y вертикально, начало
отсчета совпадает с точкой бросания (рис.19). Векторы
r
начальной скорости V0 и ускорения свободного
22
падения лежат в плоскости XOY , поэтому для описания движения достаточно двух
координат.
r
Проекции вектора начальной скорости V0 на оси X и Y соответственно равны
V0 cos α , V0 sin α , проекция вектора ускорения свободного падения на ось X равна
нулю, а на ось Y равна (− g ) . Перепишем теперь закон движения тела (3) в проекциях на
оси координат.
⎧ x = V0 t cos α
⎪
(3а)
⎨
gt 2 .
α
=
sin
−
y
V
t
0
⎪
2
⎩
Эти уравнения полностью описывают движение тела – из закона движения можно найти
любую характеристику движения. Для этого надо уметь «переводить» возникающие
вопросы на «язык» координатного описания, что мы сейчас продемонстрируем.
Траектория движения. Строго говоря, уравнения (3а) уже описывают траекторию
движения в, так называемой параметрической форме. Тем не менее, получим в явном виде
x
зависимость y (x) , для чего достаточно выразить из первого уравнения t =
и
V0 cos α
подставить его во второе:
g
y = xtgα −
x2 .
2
2
2V0 cos α
Из вида этой функции явно следует, что траекторией движения является парабола.
Время движения. Когда тело упадет, его координата y станет равной нулю, поэтому
время движения8 t1 может быть найдено из уравнения y (t1 ) = 0 :
gt12
V0 t1 sin α −
= 0.
2
2V0 sin α
.
g
Очевидно, что первый корень уравнения9 соответствует времени бросания, а второй –
времени падения.
Дальность полета. Дальность полета – это координата x в момент падения, поэтому
2V02 sin α cos α
.
S = x(t1 ) =
g
Максимальная высота подъема. Используя выражение для траектории движения,
можно заметить, что траектория движения – симметричная парабола, поэтому высоту
t
подъема можно найти как координату y в момент времени t 2 = 1 . Но сейчас мы
2
сформулируем общий метод нахождения максимального значения координаты. Если
проекция скорости V y на ось Y положительна, то координата y возрастает, если же V y
Решениями этого квадратного уравнения являются два числа t1 = 0 и
t1 =
отрицательна, то координата убывает, следовательно, максимальное
координаты достигается тогда, когда соответствующая проекция
обращается в нуль!
значение
скорости
Заметьте, что в законе движения время t является переменной величиной, аргументом функции, когда же
речь идет о конкретных моментах времени (как сейчас о времени падения), мы будем обозначать их с
соответствующими индексами, подчеркивая, что это конкретные числа.
9
Подчеркнем, что мы обязаны каждому математическому решению, даже абсурдному на первый взгляд
найти физическое истолкование. Иначе получится некая странная ситуация – в одних случаях математике
доверяем, в других нет!
8
23
Запишем выражение для скорости V y = V0 sin α − gt . Теперь из уравнения V y (t 2 ) = 0
определим
момент
времени
достижения
максимальную высоту hmax = y (t 2 ) =
максимальной
высоты
t2 =
V0 sin α
g
и
V02 sin 2 α
.
g
2.9 Определение закона движения по известной зависимости скорости от времени.
Сейчас мы покажем, что по известной произвольной зависимости скорости
движения от времени и начальному положению можно, в принципе, найти закон
движения. Решение этой задачи может вызвать определенные математические проблемы,
но, подчеркнем, эта задача разрешима.
Пусть материальная точка движется вдоль прямой, вдоль которой направим
координатную ось X . Допустим, каким-то образом, нам стала известна зависимость
скорости материальной точки от времени,
задаваемая функцией v(t ) . Проблема заключается в
построении закона движения материальной точки,
т.
е.
определении
координаты
точки
в
произвольный момент времени t - x(t ) . Эта задача
может быть разрешена следующим образом:
мысленно разобьем время движения на N малых
интервалов времени ∆t i , где i - номер интервала
времени, пробегающий ряд натуральных чисел
i = 1,2,3...N (рис. 20). Ясно, что сумма всех
временных промежутков должна быть равна
рассматриваемому временному интервалу
∆t1 + ∆t 2 + ∆t 3 + ... + ∆t N = t − t 0
Если выбранные промежутки времени достаточно малы, можно пренебречь изменением
скорости в течение этого промежутка времени. Тогда изменение координаты за малый
промежуток времени ∆ti приближенно можно считать равным ∆xi = v(ti )∆ti , где v(t i ) средняя скорость на рассматриваемом промежутке времени. Если в момент времени t 0
координата точки равна x0 , то в момент времени t координата точки рассчитывается по
формуле
x(t ) = x0 + ∆x1 + ∆x 2 + ∆x3 + ...∆x N = x0 + v1 ∆t1 + v 2 ∆t 2 + v3 ∆t 3 + ... + v N ∆t N
Естественно, чем меньше длина выбранных интервалов времени ∆t i , тем с большей
точностью мы найдем координату точки в момент времени t . Следовательно, выбирая
интервалы все более малыми, мы можем рассчитать координату точки с любой наперед
заданной точностью. Таким образом,
нахождение закона движения сводится к
утомительной математической процедуре. К счастью, давно разработаны методы
вычисления подобных сумм для произвольных зависимостей скоростей от времени. Эти
методы составляют суть интегрального исчисления. Примененный нами графический
метод определения закона движения фактически является одним из способов вычисления
подобных сумм. Подчеркнем, что проблема вычисления подобных сумм является
математической, физический смысл которой вполне очевиден – на бесконечно малом
интервале времени движение приблизительно равномерное.
Подобный подход – разбиение на очень малые интервалы с последующим
суммированием чрезвычайно широко распространен в различных физических теориях, в
дальнейшем мы будем им постоянно пользоваться. Поэтому имеет смысл использовать
24
специальные обозначения для различных сумм, которые очень давно используются в
математике.
Для
обозначения
операции
суммирования используется специальный
символ Σ - греческая буква «сигма». С
использованием этого символа любая сумма
записывается в виде
N
a1 + a 2 + a3 + ...a N =
∑a ,
i
i =1
снизу и сверху суммы указываются пределы
изменения номера слагаемого (индекса
суммирования). В тех случаях, когда
пределы суммирования очевидны, ограничиваются более краткой записью, указывая
только обозначение индекса суммирования
a1 + a 2 + a3 + .... =
ai
∑
i
С использованием обозначения суммы формула для расчета закона движения кратко
может быть записана в виде
x(t ) = x0 + v1 ∆t1 + v 2 ∆t 2 + v3 ∆t 3 + ... + v N ∆t N = x 0 +
N
∑ v ∆t .
i
i
i =1
Подчеркнем очень важное обстоятельство – для однозначного определения закона
движения мало знать зависимость скорости от времени v(t ) , необходимо еще одно
начальное условие – значение координаты x0 в некоторый момент времени t 0 .
2.10 Определение закона движения по известной зависимости ускорения от времени.
Если для материальной точки, движущейся вдоль прямой, известна зависимость
ускорения от времени a (t ) , то задача определения закона движения разбивается на два
этапа – расчет зависимости скорости от времени v(t ) , по которой рассчитывается закон
движения x(t ) . Для расчета зависимости скорости от времени можно использовать
процедуру, аналогичную рассмотренной в предыдущем разделе. Следует разбить время
движения на малые промежутки ∆t i , в течении которых движение приблизительно можно
считать равноускоренным. Изменение скорости за этот промежуток времени равно
∆vi = ai ∆t i . Если в момент времени t 0 скорость точки равнялась v 0 , то в момент времени
t скорость в момент времени t может быть рассчитана по формуле
v(t ) = v0 + a1 ∆t1 + a 2 ∆t 2 + a3 ∆t 3 + ... + a N ∆t N = v 0 +
N
∑ a ∆t .
i
i
i =1
Далее можно провести процедуру расчета координаты, описанную в предыдущем
параграфе.
Таким образом, знание зависимости ускорения точки от времени и двух
дополнительных условий (начальной скорости и начальной координаты) позволяет
построить закон движения материальной точки.
2.11 Определение закона движения – основная задача кинематики.
Мы определили кинематические характеристики механического движения – скорость, ускорение
(скорость изменения скорости). В общем случае ускорение также может изменяться в процессе движения,
поэтому можно было бы ввести и такую характеристику движения как «скорость изменения ускорения».
Однако, она уже является излишней, так законы динамики позволяют находить именно ускорение
движения. Поэтому основная задача кинематики в самой общей постановке формулируется следующим
25
образом: по известной зависимости ускорения от времени, координаты и скорости найти закон
движения тела.
Рассмотрим общий алгоритм решения уравнений динамики, которые имеют вид
a = f (t , x, v) ,
(1)
где a =
∆x
∆v
, ускорение точки, движущейся вдоль оси X , v =
- скорость тела, f - отношение суммы
∆t
∆t
сил, действующих на тело, к массе тела. Действительно, на тело могут действовать силы, которые зависят от
координат (силы упругости, гравитационного, электрического и магнитного взаимодействий и т.д.),
скорости (рассматриваемая сила сопротивления воздуха, сила Лоренца и т.д.), от времени (внешние
переменные силы). Поэтому уравнение (1) является наиболее общим.
Трудно предложить что-нибудь более оригинальное, чем в очередной раз разбить время движения
на малые промежутки времени ∆t и попытаться определить приближенные значения координаты
xk
и
скорости vk в дискретные моменты времени t k = t 0 + k∆t ( k = 1,2,3... ). Зная начальные условия (при
t = t 0 x = x 0 ; v = v0 ) по формуле (12) можно вычислить начальное ускорение a0 = f (t 0 , x0 , v0 ) . В
течение малого промежутка времени ∆t можно пренебречь изменением ускорения и считать движение
равноускоренным. В этом приближении скорость и координата тела по окончании промежутка
∆t рассчитываются по формулам
v1 = v0 + a0 ∆t
x1 = x0 + v0 ∆t +
2
a0 (∆t ) .
2
Далее расчет можно продолжить: вычислить ускорение в момент времени t1 , считая его постоянным в
течение следующего промежутка ∆t , найти скорость и ускорение в следующий момент времени и т.д.
Таким мы приходим к пошаговому алгоритму определения закона движения по известной
зависимости ускорения тела от времени, координат и скорости. Этот метод называется методом Эйлера и
выражается формулами:
ak = f (t k , xk , vk );
vk +1 = vk + ak ∆t ;
.
ak (∆t )
2
2
xk +1 = xk + vk ∆t +
Подчеркнем, что описанный метод решения основной задачи механики носит скорее теоретический
характер – он является доказательством принципиальной разрешимости поставленной задачи. При решении
большинства задач он используется крайне редко – разработаны более совершенные методы, иногда
позволяющие получит аналитическое (в виде формулы) выражение для закона движения. Для решения
многих задач механики используются чрезвычайно сложные математические методы, более того, именно
потребности механики во многом стимулировали развитие математики (достаточно сказать, что основы
дифференциального и интегрального исчислений были разработаны И. Ньютоном для решения
механических задач). Правда, число задач, допускающих аналитическое решение, невелико, поэтому в
настоящее время для расчета движения широко используют приближенные компьютерные методы,
позволяющие получить решение с любой требуемой точностью. Суть этих методов и сводится к разбиению
движения на малые интервалы, аналогично рассмотренному методу Эйлера.
Самое существенное в нашем изложении – убежденность в том, что знание зависимости
ускорения от времени, координат и скорости, а также начальных условий (координат и скоростей в
некоторый момент времени), позволяет рассчитать закон движения любой механической системы.
Задание для самостоятельной работы.
1. Пусть для материальной точки, движущейся вдоль оси X , известна зависимость
скорости точки от координаты v( x ) . Построим график зависимости величины
1
обратной скорости
от координаты. Какой смысл имеет площадь под графиком
v( x )
1
? Разработайте процедуру расчета закона движения материальной
зависимости
v( x )
точки x(t ) по известной зависимости v( x ) .
26
2.12 Относительность движения.
Когда мы рассуждали о координатах, мы подчеркивали, что указание координат
имеет смысл только тогда, когда указана, задана система координат. Поэтому координаты
точки являются относительными физическими величинами. Поэтому относительными
являются и изменения координат с течением времени, иными словами относительным
является само механическое движение10. Выбор системы координат, в принципе,
произволен и определяется главным образом удобством описания, или личными вкусами
исследователя - так, например, некоторым приятно описывать свое движение среди
неподвижных звезд. Отсутствие единой, всеобщей системы координат приводит к тому,
что все системы отсчета являются равноправными, движение в разных системах отсчета
должно описываться принципиально одинаково. Мы, конечно, не утверждаем, что
уравнения движения будут одинаковы во всех системах отсчета, в одних они будут проще,
в других сложнее, но методы описания, его результаты должны быть одинаковы - так если
два тела должны столкнуться в одной системе отсчета, то такой же результат должен быть
и в другой системе. Реально, в природе существуют материальные тела, которые
движутся, взаимодействуют, видоизменяются - а наше описание движения в конкретных
системах отсчета является всего лишь попыткой построить его более-менее приличную
модель. Согласование описания движения, переход из одной системы координат в другую
является очень важной физической задачей, далеко выходящей за рамки проблем
кинематики. В данном параграфе мы рассмотрим эту проблему только с точки зрения
кинематического описания. Для простоты и удобства графических иллюстраций мы будем
изображать системы координат на плоскости, обобщение на случай трехмерного
пространства очевидно, а при векторной записи остается тем же самым, кроме того, будем
полагать, что соответствующие оси координат параллельны. Произвольная ориентация
координат, добавляет не много физического содержания, а математическое описание
становится более громоздким.
Рассмотрим
две
системы
координат11:
исходную XOY , и смещенную X ′O ′Y ′ (рис. 21).
Координаты начала отсчета O ′ смещенной системы
координат в исходной системе обозначим ( x0 , y0 ) , а
v
радиус-вектор этой точки r0 . Тогда связь между
координатами материальной точки A в этих
системах определяется формулами
⎧ x = x0 + x ′
,
(1)
⎨
⎩ y = y0 + y′
которые можно записать в компактной векторной
форме
r r r
r = r0 + r ′ .
(2)
Эти формулы очевидны для неподвижных систем
отсчета и неподвижных тел, сейчас нам необходимо обобщить их на случай описания
движения. То есть нам из системы координат необходимо сделать систему отсчета,
добавив в каждую из них часы. У нас пока нет никаких оснований считать, что
одинаковые часы в разных системах отсчета будут идти по-разному. Поэтому будем
10
Относительность движения можно понимать в нескольких смыслах. Во-первых, тело покоящееся в одной
системе отсчета может двигаться относительно другой системы. Во-вторых, кинематические
характеристики движения - координаты, скорость, ускорение зависят от системы отсчета. Говоря об
относительности движения, будем подразумевать именно второй его смысл.
11
Напомним, что названия «исходная» и «смещенная» условны - ничего не изменится, если их поменять
местами.
27
полагать, что время в разных системах отсчета одинаково и начала отсчета времени также
совпадают
t = t′ .
(3)
r
r ∆r ′
относительно смещенной
Пусть точка A движется с некоторой скоростью v ′ =
∆t
системы координат. Найдем скорость точки в исходной системе отсчета XOY . Для этого
воспользуемся формулой (2):
r r
r
r
r
r ∆r ∆ (r0 + r ′) ∆r0 ∆r ′ r
v=
= v′ ,
+
=
=
(4)
∆t
∆t
∆t
∆t
r
при выводе мы учли, что вектор r0 является постоянным и его изменение равно нулю.
Таким образом, мы показали, что при переходе из одной неподвижной системы отсчета в
другую скорость точки не изменяется. Впрочем, этот результат очевиден - течение
времени и перемещение точек одинаковы в обеих системах отсчета. Если скорости точек
не изменяются, то не будут изменяться и их ускорения, так они выражаются через
изменение скоростей.
Пусть система X ′O ′Y ′ движется относительно системы XOY с постоянной
r
скоростью V . В любой момент времени соотношения между координатами выражаются
соотношениями (1)-(2). В случае движущейся системы координат, мы не можем логически
строго утверждать, что течение времени будет таким же, как и в неподвижной системе.
Вопрос о том, изменится ли ход часов, если они будут двигаться с постоянной скоростью,
не может быть разрешен путем логических рассуждений. Ответ на него может дать только
эксперимент, только опыт. Мы еще не раз будем возвращаться к этой проблеме, тока же
примем как аксиому, подтвержденную многовековым опытом человечества, что течение
времени одинаково в различных системах отсчета, движущихся друг относительно друга с
постоянной скоростью.
Найдем соотношение между скоростями точки в подвижной12 X ′O ′Y ′ и
неподвижной XOY системах координат. Опять воспользуемся соотношением (2) для
вычисления скорости в неподвижной системе отсчета
r r
r
r
r
r ∆r ∆ (r0 + r ′) ∆r0 ∆r ′ r r
v=
= V + v′ ,
+
=
=
(5)
∆t
∆t
∆t
∆t
r
r
∆r0 r
∆r ′ r
легко заметить, что
= V - скорость движения подвижной системы, а
= v′ ∆t
∆t
скорость точки относительно подвижной системы координат. Довольно часто
применяется следующая терминология: Скорость точки относительно подвижной системы
r
координат v ′ называют относительной скоростью, скорость точки относительно
неподвижной системы координат называют абсолютной скоростью, а скорость одной
системы координат относительно другой называю переносной скоростью. Используя эти
названия, очень важное соотношение (5) можно словесно сформулировать в виде:
Абсолютная скорость точки равна сумме ее относительной скорости и
переносной скорости.
Из соотношения (5) можно выразить относительную скорость
r r r
v′ = v −V ,
(6)
относительная скорость точки равна разности между ее абсолютной скоростью и
переносной скоростью.
Заметьте, что соотношению (6) можно дать и другое истолкование. Будем считать систему
отсчета X ' O' Y' неподвижной, а систему XOY подвижной. Тогда переносная скорость
12
Очередной раз отметим условность названий систем отсчета - если одна система движется относительно
другой, то справедливо и обратное - выбор неподвижной и движущейся систем остается за исследователем.
28
r
(то есть скорость системы XOY относительно X ' O' Y ' ) будет равна (−V ) , поэтому
соотношение (6) просто совпадает с формулой (5).
r
Подведем итог: при равномерном движении системы X ' O' Y ' со скоростью V
относительно системы XOY радиус-вектор начала отсчета подвижной системы
r
r
изменяется по закону r0 = V0 t , поэтому координаты точки и времена в этих системах
отсчета связаны соотношениями
r r r
r = r ′ + V0 t
,
(7)
t = t′
Эти преобразования называются преобразования Г. Галилея, и играют чрезвычайно
важную роль в классической физике.
Соотношения между скоростями (5)-(6) выполняются в любой момент времени,
поэтому их можно использовать для того, чтобы установить связь между ускорениями
точек в различных системах координат. Пусть точка A движется с ускорением
r
a ′ относительно подвижной системы координат (будем по-прежнему считать, что
переносная скорость является постоянной), тогда ее ускорение в неподвижной системе
можно вычислить по следующим формулам
r r
r
r
r ∆v ∆(V + v ′) ∆v ′ r
a=
=
=
= a′ .
(8)
∆t
∆t
∆t
Мы доказали, что если одна система движется относительно другой с постоянной
скоростью, то ускорения тел относительно этих систем отсчета одинаковы. Иными
словами, ускорение является инвариантной величиной при переходе из одной системы
отсчета в другую.
Наше изложение можно продолжить в том же духе - рассмотреть случай ускоренного движения
одной системы относительно другой. Однако сейчас мы не будем заниматься этим, так как при изучении
динамики мы увидим, что системы движущиеся друг относительно друга равномерно и прямолинейно
занимают особое место в механике, именно им уделяется особое внимание, на что есть весьма серьезные
физические причины.
29
§3 Криволинейное движение. Плоскопараллельное движение твердого тела.
Рассмотренное ранее произвольное движение в трехмерном пространстве и его
векторное и координатное описание, в принципе, универсально. Однако во многих
случаях предпочтительнее использовать иные подходы. Так при движении по известной
траектории материальная точка обладает одной степенью свободы, поэтому ее движение
может быть полностью задано с помощью одной функции (а не трех, как в случае
использования декартовых координат). Кроме того, при построении уравнений движения
часто также удобнее использовать координаты, отличные от декартовых. В связи с этим
есть необходимость рассмотреть отдельно криволинейное движение, существенной
особенностью которого является изменение направления вектора скорости и
существования ускорения, описывающего изменение направление скорости.
3.1. Равномерное движение точки по окружности.
Движение по окружности является достаточно распространенным в окружающем
нас мире - при вращении любого твердого тела вокруг фиксированной оси, все точки
этого тела движутся по окружностям. Так как все
окружности подобны, то достаточно описать движение
одной из них, чтобы описать вращение всего твердого тела.
Кроме того, равномерное движение по окружности является
простейшим криволинейным движением.
Пусть материальная точка движется с постоянной по
модулю скоростью v по окружности радиуса R . При таком
r
движении направление вектора скорости v постоянно
изменяется (рис. 22), следовательно, как и при любом
криволинейном движении, движение по окружности есть
движение с ускорением.
Рассмотрим изменение вектора скорости тела за малый промежуток времени ∆t
(рис. 23). Обозначим положение точки, движущейся по окружности радиуса R , в
r
некоторый момент времени A0 . Вектор скорости v0 в этот момент направлен по
касательной к окружности, то есть перпендикулярно радиусу OA0 . За время ∆t частица
r
переместилась в точку A1 , ее скорость v1 изменила
направление и стала перпендикулярна радиусу OA1 (но
r
r
модуль ее остался неизменным v0 = v1 = v ). Для того
чтобы вычислить изменение скорости, совместим
r
r
началу векторов v0 и v1 . Тогда треугольник,
образованный векторами скоростей
подобен
треугольнику OA0 A1 . Из подобия этих треугольников
следует
∆v A0 A1
=
.
(1)
v
R
Если рассматривать изменение положения частицы и ее скорости за очень малый
промежуток времени, то длина хорды A0 A1 будет очень близка к длине дуги A0 A1
∆v v∆t
v2
, откуда получаем ∆v = ∆t . Таким образом модуль
=
R
v
R
ускорения точки равен
∆v v 2
a=
= .
(2)
∆t R
s = v∆t , поэтому
30
Чтобы полностью определить вектор ускорения, необходимо выяснить его направление.
r
r
Заметим, что при малой величине ∆t , угол между векторами v0 и v1 крайне мал, поэтому
можно считать, что вектор изменения скорости направлен перпендикулярно1 как вектору
r
r
v0 , так и вектору v1 . Следовательно, вектор ускорения в данном случае направлен к
центру окружности.
Вектор ускорения точки при ее равномерном движении по окружности
v2
направлен к центру окружности, а его модуль равен
. Такое ускорение называется
R
центростремительным.
Как мы уже отмечали ранее, материальной точка, движущаяся по заданной линии,
обладает одной степенью свободы, поэтому ее положение однозначно определяется одной
координатой. В случае движения точки по окружности в качестве такой единственной
координаты удобно выбрать угол поворота.
Математическое отступление - радианная мера угла.
Градусная мера измерения углов оказывается не слишком удобной при описании механического движения.
Поэтому в физике чаще используется другая единица измерения углов. Напомним, углом называется часть
плоскости, ограниченная двумя лучами. Построим внутри угла несколько дуг окружностей разных
радиусов, центры которых совпадают с вершиной угла. Длина дуги s , заключенной внутри угла, конечно,
зависит от ее радиуса, однако отношение длины дуги к ее радиусу зависит только
от величины угла
s1 s 2 s3
=
= , поэтому это отношение может служить мерой
r1 r2 r3
угла.
Таким образом, радианной мерой угла называется отношение длины дуги
окружности с центром в вершине угла и расположенной внутри угла, к ее
радиусу
ϕ=
s
.
r
Легко установить соответствие между радианной и градусной мерой. Так как длина окружности
равна s = 2πr , то полный угол равен ϕ = 2π радиан2. Соответственно, развернутый угол равен π радиан,
прямой угол формулами
π /2
радиан. В общем виде связь между градусной
ϕ° =
1 радиан равен
180°
π
180°
π
ϕ; ϕ =
π
180°
ϕ°
ϕ°
и радианной
ϕ
мерой выражается
(3)
≈ 57,3° .
Основные достоинства радианной меры заключаются в том, что, во-первых, единица измерения
радиан является безразмерной величиной (отношение двух длин), во-вторых, очень просто выражается
длина дуги через радиус и величину угла s = rϕ . Связывая меру угла с длиной дуги, мы можем
рассматривать углы произвольной величины - большие чем угол 2π ( 360° ). Таким углам соответствует
дуга несколько раз охватывающая целую окружность - так, например, угол поворота ϕ = 10π равен 5
полным оборотам. Это очень удобно при описании вращательного движения - чем больше вращается тело,
тем больший угол его поворота. Конечно, при движении по окружности материальная точка регулярно
проходит через одни и те же положения в пространстве, поэтому, зная угол поворота, мы однозначно
определим положение точки, но, зная только положение точки (например, ее декартовые координаты), мы
не можем однозначно определить угол поворота, так как нам не известно, сколько оборотов совершила
данная точка к данному моменту времени.
1
Иными словами вектор скоростей представляет собой равнобедренный треугольник с очень малым углом
при его вершине, тогда равные углы при основании треугольника будут близки к прямым.
2
Часто наименование радиан опускают и говорят: «полный угол равен 2π , прямой угол равен π / 2 » и
т.д.
31
Пусть материальная точка движется по окружности радиуса R . Введем декартовую
систему координат, начало которой совместим с центром
окружности (рис. 24). Положение точки на окружности
однозначно определяется углом ϕ между осью X и радиусвектором точки.
Конечно, оси координат можно направить произвольно,
да и угол можно отсчитывать и от оси Y , однако мы в
дальнейшем для однозначности будем отсчитывать угол
поворота от оси X , в направлении против часовой стрелки.
Декартовые координаты точки однозначно выражаются
через угол поворота по формулам
⎧ x = R cos ϕ
.
(4)
⎨
⎩ y = R sin ϕ
При движении точки ее координата, то есть угол поворота, изменяется, становится
функцией времени. Поэтому закон движения в этом случае представляется функцией
ϕ (t ) - зависимости угла поворота от времени.
По аналогии с одномерным движением введем понятие угловой скорости.
Угловой скоростью ω называется отношение угла поворота к промежутку
времени, в течение которого этот поворот произошел, при промежутке времени,
стремящемся к нулю
∆ϕ
(5)
ω=
, при ∆t → 0 .
∆t
рад
Единицей угловой скорости является
- «радиан в секунду», однако, так как радиан
с
является безразмерной величиной, то размерность угловой скорости может быть просто
1
= с −1 «секунда в минус первой степени».
с
При равномерном движении по окружности угловая скорость является постоянной
и равна углу поворота в единицу времени. Время одного оборота (эту величину еще
называют период вращения) T легко найти, если вспомнить, что один оборот
соответствует углу поворота 2π , поэтому
2π
T=
.
(6)
ω
Число оборотов в единицу времени называют частотой вращения, и она вычисляется по
формуле
1 ω
n= =
.
(7)
T 2π
Установим связь между угловой и линейной скоростями при движении
материальной точки по окружности. Модуль линейной скорости определяется как
отношение пройденного пути к промежутку времени, за который этот путь пройден
s
v = , а при движении по окружности длина пути (длина дуги окружности) выражается
∆t
через угол поворота (выраженный в радианах) s = R∆ϕ , поэтому
R∆ϕ
v=
= Rω .
(8)
∆t
Запишем также выражение для центростремительного ускорения, используя
понятие угловой скорости,
v 2 ( Rω ) 2
a=
=
= Rω 2 .
(9)
R
R
32
Специально отметим, что формулы (8) и (9) остаются справедливыми при
движении по окружности и в том случае, когда скорость точки изменяется по абсолютной
величине. Так при выводе формулы (8) можно рассмотреть случай ∆t → 0 , в таком
пределе скорость v будет являться мгновенной скоростью, а ω - мгновенной угловой
скоростью.
При вращении вокруг фиксированной оси направление вращения может иметь только два значения:
«по часовой стрелке» и «против часовой стрелки». Поэтому в этом случае можно говорить о двух знаках
угловой скорости, обычно, плюс, при вращении против часовой стрелки и минус при вращении по часовой
стрелке. Для того чтобы описать произвольное вращение необходимо задать также ось вращения.
Оказывается удобным задавать ось вращения с помощью вектора, направленного вдоль этой оси. Если
r
совместить эти две характеристики вращения, то получим вектор угловой скорости ω , направление
которого совпадает с осью вращения, а модуль равен определенной нами угловой скорости. Использую
математическую операцию векторного произведения можно записать выражение для связи между линейной
r
r
r
и угловой скоростями v = r × ω . Аналогично можно определить вектор углового ускорения
r
ε =
r
∆ω
,
∆t
который определяет не только изменение скорости вращения, но и изменение оси вращения.
3.2 Движение материальной точки по произвольной кривой.
Если угловая скорость не является постоянной, то имеет смысл ввести понятие
углового ускорения, которое мы обозначим греческой буквой ε («эпсилон»).
Угловым ускорением называется отношение изменения угловой скорости к
промежутку времени, в течение которого это изменение произошло, при промежутке
времени, стремящемся к нулю.
∆ω
ε=
, при ∆t → 0 .
(1)
∆t
Используя связь между линейной и угловой скоростями, эту формулу можно
переписать в виде
∆ω 1 ∆v
ε=
=
.
∆t R ∆t
Заметим, что в данном выражении в числителе стоит изменение модуля скорости (а
не вектора скорости!). Полное же ускорение - отношение изменения вектора скорости к
промежутку времени, таким образом, оказывается состоящим из двух частей - одна из
которых описывает изменение направления вектора скорости (это ускорение является
центростремительным или нормальным3), а вторая - изменение модуля скорости (это
ускорение называется касательным или тангенциальным).
Если направление вектора скорости не изменяется, то вектор ускорения направлен
вдоль той же прямой, что и скорость, поэтому следует считать, что вектор
тангенциального ускорения совпадает с направление вектора скорости, если скорость
возрастает и противоположен ему, если величина скорости убывает.
При движении материальной точки по
произвольной кривой, малый участок траектории
можно приближенно заменить небольшой дугой
окружности. Для этого следует воспользоваться
следующим способом построения такой окружности,
который аналогичен построению касательной
прямой. Напомним, что касательную можно считать
предельным положением секущей прямой.
Возьмем слева и справа от точки A две точки
A′, A′′ , лежащие на заданной линии (рис. 25).
Проведем через эти три точки окружность секущую
C ′ , (если три точки лежат на одной прямой, то мы
3
Название «нормальное» происходит от математического термина «нормаль» - то есть перпендикуляр.
33
будем считать эту прямую окружностью очень большого радиуса). После этого начнем
мысленно приближать точки A′, A′′ к точке A , соответственно изменяя секущую
окружность. При стремлении точек A′, A′′ к точке A секущая окружность будет
стремиться к предельному положению C0 . Эта предельная окружность называется
соприкасающейся в точке A , ее радиус называется радиусом кривизны линии в данной
точке, а центр центром кривизны.
Таким образом, движение по произвольной кривой на малом участке можно
рассматривать как движение по соприкасающейся окружности.
r
Вектор скорости v частицы всегда направлен по
касательной к линии траектории движения, а вектор ускорения
можно разложить на две составляющие (см. рис. 26) - одна из
r
них, тангенциальное ускорение at , описывает изменение модуля
скорости и направлено по касательной к траектории, а другая,
r
нормальное ускорение an , описывает изменение направления
вектора скорости и направлено перпендикулярно касательной
(по нормали) к центру кривизны траектории (в сторону ее
вогнутости). Модули этих компонент ускорений рассчитываются по формулам
v2
∆v
at =
= εR;
an =
= ω 2R ,
(7)
R
∆t
где R - радиус кривизны траектории в данной точке.
r
r
Сумма векторов ускорений at и a n является вектором
r
полного ускорения a . Конечно, вектор полного ускорения можно
r
r
представить в виде суммы проекций a x и a y на произвольно
выбранные оси координат (рис. 27). Но разложение вектора на
нормальную и тангенциальную составляющие имеет два
r
r
существенных преимущества: первое, обе компоненты at и a n
имеют явные физический смысл; второе, такое разложение
«привязывается» не к произвольно выбранной системе координат, а
непосредственно к траектории движения и вектору скорости.
3.3 Суперпозиция движений.
Мы изучили несколько простейших моделей движения. Сейчас постараемся
показать, как из этих простых движение можно «конструировать» более сложные и
красивые движения. Слово «суперпозиция» обозначает сложение, наложение, сочетание оно очень часто используется в физике. Возможность такого наложения различных видов
движения обусловлена возможностью описывать его в различных системах отсчета и
r r r
переходить из одной системы в другую по формулам r = r0 + r ′ . Теперь мы можем
r
задавать независимо закон движения в подвижной системе отсчета r ′(t ) , закон движения
r
самой движущейся системы r0 (t ) и получать более сложный закон движения. Далее может
быть, что и неподвижная система отсчета движется относительно другой «еще более
неподвижной» системы, тем самым добавляется еще одно слагаемое и т.д. На этом пути
открываются практически неограниченные возможности, рассмотреть их всех
невозможно, поэтому мы вынуждены ограничиться несколькими простыми, но красивыми
движениями.
Движение тела, брошенного под углом к горизонту можно представить в виде
суперпозиции равномерного движения вдоль горизонтальной оси и равноускоренного
движения вдоль вертикальной оси. Такой «суперпозиции» можно придать наглядный
смысл: пусть в вагоне равномерно и прямолинейно движущегося поезда вверх подброшен
небольшой шарик. В системе отсчета, связанной с вагоном, шарик движется вдоль
вертикальной прямой с постоянным ускорением свободного падения. А в системе отсчета,
34
связанной с землей, движение шарика будет движением по описанной ранее параболе.
Отметим также, что «разложение движения на составляющие» не является однозначным4.
Так то же движение тела, брошенного под углом к горизонту, можно представить в виде
«суммы» равномерного движения вдоль прямой направленной под углом к горизонту,
задаваемой вектором начальной скорости, и
равноускоренного движения вдоль
вертикальной прямой. Фактически эти разложения мы использовали ранее при описании
этого движения.
Суперпозиция вращательного и
поступательного
движений.
Пусть материальная точка А
движется по прямому стержню с
V, а
постоянной скоростью
стержень вращается вокруг оси с
постоянной угловой скоростью ω .
Совместим начало системы отсчета
с осью вращения (рис. 28). Тогда
расстояние от точки А до начала
отсчета и угол поворота стержня
зависят от времени по законам l = Vt , α = ωt .
Зависимость декартовых координат точки от времени имеет вид
x = l cos α = Vt cos ωt
x = l sin α = Vt sin ωt
и описывает движение по спирали.
Еще одна суперпозиция поступательного и вращательного движений.
Пусть колесо радиуса R катится по горизонтальной поверхности без
проскальзывания. Точка А расположена на расстоянии a от оси колеса (будем считать,
что a может быть как меньше, так и больше R - такие точки можно найти, например, на
железнодорожном колесе). Построим семейство траекторий точек колеса.
Пусть в начальный момент времени центр
колеса находится в точке O , введем систему
координат, ось X которой проходит вдоль
поверхности, по которой катится колесо, а ось Y
перпендикулярна этой поверхности и проходит
через точку O (рис. 29). Выберем точку А на
расстоянии a от центра и первоначально
находящуюся на оси Y . Посмотрим как
изменится положение этой точки, когда колесо
повернется на некоторый угол ϕ = ωt (на рис. это
∠A′O ′D ). Центр колеса сместится на расстояние
S и займет положение O' , а точка A окажется в точке A’. Так как движение происходит
без проскальзывания, то смещение колеса S = OO ′ = BD будет равно длине дуги DB ′ .
Поэтому S = Rϕ , где угол
ϕ , естественно, измеряется в радианах. Координаты цента
колеса будут равны xO′ = S = Rϕ , y O′ = R . Рассматривая треугольник O ′A′C , легко
найти координаты рассматриваемой точки A’:
⎧ x = Rϕ − a sin ϕ = Rωt − a sin ωt
.
⎨
⎩ y = R − a cos ϕ = R − a cos ωt
4
Дискуссия о том какое разложение является «правильным» равносильна спору о том, какое разложение
«7=5+2» или «7=3+4» точнее описывает свойства «семерки».
35
Посмотрите на эти траектории (рис.30) при a , изменяющемся от − 3R до 3R (с
шагом R ). Не правда ли, эффектные кривые!
4
Суперпозиция двух вращательных движений.
Посмотрим, какую траекторию описывает точка
M колеса радиуса r , катящегося без скольжения по
другой неподвижной окружности радиуса R (рис. 31).
r
Обозначим ϕ = ωt -угол поворота колеса, m =
R
отношение радиусов колеса и неподвижной окружности.
Пусть A -начальное положение рассматриваемой точки.
Из геометрических соображений можно получить
параметрическое уравнение траектории точки М:
⎧ x = ( R + r ) cos mϕ − r cos(ϕ + mϕ )
.
⎨
⎩ y = ( R + r ) sin mϕ − r sin(ϕ + mϕ )
Вид траектории полностью определяется параметром m . Если этот параметр является
p
рациональным числом m = , ( p, q - целые числа), то траектория является замкнутой.
q
Посмотрите на различные траектории, описываемые этими уравнениями (рис. 32). На всех
рисунках - в центре изображение той окружности, по которой катится колесо.
36
3.4 Суперпозиция и линейность.
Возможность «сложения» движений и соответствующих кинематических
характеристик имеет и математическое воплощение. Поясним эту взаимосвязь на
простейшем примере.
Пусть материальная точка А движется с угловой
∆α'
по окружности радиуса r с центром,
скоростью ω' =
∆t
совпадающим с началом координат системы отсчета
X ' OY ' , которая в свою очередь вращается с угловой
∆β
относительно неподвижной системы
скоростью ω 0 =
∆t
отсчета XOY . Угол поворота точки относительно
неподвижной системы отсчета, как следует из
элементарных геометрических соотношений равен
α = α '+ β . Поэтому угловая скорость вращения относительно неподвижной системы
∆α
= ω '+ω 0 . Вычислим теперь, с
отсчета также равна сумме угловых скоростей ω =
∆t
каким центростремительным ускорением движется точка А. Во вращающейся системе
2
отсчета X ' OY ' это ускорение равно a' = r (ω ') . Ускорение подвижной системы отсчета
относительно неподвижной -
a 0 = r (ω 0 ) . Ускорение же точки А относительно
2
неподвижной системы отсчета a = r (ω '+ω 0 ) ≠ a '+ a 0 . Таким образом, для угловых (и
обычных) скоростей принцип суперпозиции выполняется, а для ускорений нет! Легко
заметить, что нарушение принципа суперпозиции для ускорений обусловлено
квадратичной зависимостью ускорения от скорости. Скорость же линейно5 (в данном
случае даже пропорциональна) выражается через углы поворота.
В общем случае можно утверждать, что математическим выражением
принципа суперпозиции для какой-либо физической величины является линейность
уравнений, определяющих эту величину.
2
3.5 Описание движения твердого тела.
Кинематическое описание движение
твердого тела представляет собой гораздо более
сложную математическую задачу, чем описание
движения материальной точки, уже хотя бы
потому, что твердое тело обладает шестью
степенями свободы, материальная точка только
тремя. Представьте себе полет кувыркающегося
в воздухе бруска, и вы сразу оцените сложность
описания его движения. Основной подход к
математическому описанию движения твердого
тела заключается в разложении его движения на
составляющие - движение какой-либо точки
тела относительно неподвижной системы
координат и вращение тела относительно этой
точки.
Если задавать закон движение одной
точки мы уже научились, то описывать вращение вокруг изменяющейся в пространстве
5
Напомним, что линейная зависимость между величинами y и x выражается уравнением y = kx + b , где
k, b - постоянные. Если в этой зависимости b = 0 , то говорят, что y и x пропорциональны друг другу.
37
оси весьма сложно. Только для того, что бы продемонстрировать проблемы, которые
возникают при этом, покажем, что результат двух поворотов вокруг различных осей
зависит от порядка, в котором они проводятся. На рисунке 34 показаны результаты двух
поворотов, проведенных в разном порядке - как видите результат не один и тот же!
3.6 Плоскопараллельное движение.
Движение твердого тела называется плоскопараллельным, если траектории
движения всех его точек являются плоскими кривыми, лежащими в параллельных
плоскостях.
Плоскопараллельное движение твердого тела можно представить как суперпозицию
поступательного движения и вращения вокруг оси, направление которой не изменяется.
Наглядными примерами такого движения являются качение колеса, движение книги без
отрыва от стола и т.д.
Для описания положения абсолютно твердого
тела при плоскопараллельном движении необходимо
задать две декартовые координаты какой-либо точки
тела6 и угол его поворота, то есть плоскопараллельное
движение обладает тремя степенями свободы.
Выберем внутри тела две точки A, B ; зададим
координаты x A , y A
точки A и угол ϕ , который
образует отрезок AB с направлением оси X . Три числа
x A , y A и ϕ однозначно определяют положение тела на
плоскости, следовательно, являются его координатами.
Зная эти координаты, можно определить положение в
пространстве любой другой точки твердого тела путем геометрических построений.
Покажем теперь, как можно найти скорость любой точки твердого тела при
плоскопараллельном движении (рис. 36). Разложим движение
r на две составляющих поступательное движение, скорость которого обозначим V , и
вращение вокруг оси, проходящей через точку A , с угловой
∆ϕ
скоростью ω =
. Тогда скорость любой другой точки тела
∆t
(например,
B ) является векторной суммой скоростей
поступательного и вращательного движений r
r r
V B = V + Vвр . ,
(1)
причем вектор скорости вращательного движения направлен
перпендикулярно отрезку AB и равен по абсолютной величине
Vвр. = ωr , где r расстояние от точки B до оси вращения.
Рассмотрим катящееся без проскальзывания колесо
R (рис. 37). Пусть его центр движется со скоростью
радиуса
r
V . Найдем скорости некоторых других точек колеса. Для этого
представим движение колеса как сумму поступательного
движения его центра и вращения вокруг его оси. Так как
движение происходит без проскальзывания, то угловая
V
скорость вращения определяется формулой ω = . Для точек,
R
находящихся
на
ободе
колеса
линейная
скорость
6
С точки зрения кинематического описания выбор этой точки произволен - только следует стремиться к
тому, чтобы траектория этой точки была по проще. Далее мы укажем как можно легко найти такую точку.
38
вращательного движения равна по модулю скорости поступательного движения, так как
для них расстояние до оси вращения равно радиусу колеса, поэтому
V
Vвр. = ωr = R = V . Однако, направление этой скорости различно для разных точек. Так,
R
для точки A скорость вращательного движения направлена горизонтально, также как и
скорость поступательного движения. Поэтому суммарная скорость точки A равна 2V и
направлена горизонтально. Скорость вращательного движения точки B направлена
вертикально вверх, поэтому ее полная скорость направлена под углом 45° к горизонту, а
ее модуль VB = V 2 . Очень интересна точка касания с поверхностью C : скорость ее
вращательного движения направлена горизонтально в сторону противоположную
скорости поступательного движения, поэтому ее полная скорость равна нулю.
Так как разложение движение на составляющие не является однозначным, можно
теперь представить качение колеса как сумму движения точки C и вращения вокруг оси,
проходящей через эту точку. Мы показали, что скорость точки C равна нулю, поэтому
появляется возможность рассматривать движение колеса как чистый поворот вокруг
точки C . Правда, это возможно в течение только бесконечно малого промежутка
времени, потому, что в следующий момент точкой касания будет другая точка колеса.
Множество точек твердого тела, скорости которых в данный момент равны нулю,
образуют мгновенную ось вращения тела. Такая ось существует при любом движении
твердого тела. Правда положение этой оси постоянно изменяется, поэтому для
вычисления координат точек такое представление движения не дает особых преимуществ.
Но для вычисления скоростей точек, рассматривать плоскопараллельное движение как
чистый поворот очень удобно.
Легко доказать, что угол поворота тела не зависит от того, относительно какой оси
мы его рассматриваем, следовательно, и угловая скорость не зависит от оси. С этой точки
зрения, скорость любой точки колеса определяется формулой V = ωr ′ , где r ′ - расстояние
от данной точки до мгновенной оси вращения.
Рассмотренная задача об определении скоростей
точек катящегося колеса может быть легко решена, если
рассматривать его движение как поворот вокруг точки C
(рис. 38): точка A находится на расстоянии 2 R от
мгновенной оси вращения, поэтому ее скорость равна
V A = 2 Rω = 2V ; точка B находится на расстоянии R 2 от
оси, ее скорость V 2 . Направления векторов скоростей
также совпадают с полученными ранее.
Таким образом, мы имеем два примерно одинаковых
по сложности способа описания движения твердого тела:
первый - суперпозиция поступательного и вращательного
движений: второй - поворот вокруг мгновенной оси.
39
§ 4 Основные законы динамики.
В предыдущем разделе «Кинематика» мы рассмотрели математические
способы описания механического движения. Фактически мы занимались
математикой - переводом расплывчатого словесного описания на точный и
однозначный язык математических формул, функций, графиков и.д. Сейчас нам
предстоит выяснить физические причины, приводящие к тому или иному виду
движения, раздел механики, изучающий причины движения и его изменения
называется динамика.
4.1 Закон инерции. Принцип относительности Галилея.
Повседневный жизненный опыт показывает, что для того чтобы какое
либо тело двигалось к нему необходимо прикладывать определенные усилия1 для передвижения человек и животные используют свои мышцы, все средства
транспорта снабжены двигателями, если не подталкивать скользящую по льду
шайбу, то она останавливается, вы можете без труда продолжить этот ряд
примеров. Поэтому складывается впечатление, что причиной движения тела
является воздействие на него других тел. Такая точка зрения господствовала в
научных представлениях человечества в течение полутора тысяч лет.
Приходилось даже придумывать экзотические объяснения для
объяснения простых движений. Так, например, для объяснения полета стрелы,
выпущенной из лука, была придумана такая замысловатая теория. Стрела
движется в воздухе, воздушная среда перед стрелой является более
разряженным, а позади нее более плотным, и именно этот более плотный воздух
постоянно подталкивает стрелу в полете.2
Однако посмотрим на движение с иной точки зрения, попытаемся более
подробно рассмотреть результаты воздействия одного тела на другое.
Пусть некоторое тело, например, тяжелый металлический шар, падает с
некоторой высоты на поверхность земли. Он начинает двигаться под действием
притяжения к земле, в ходе падения его скорость возрастает. Экспериментально
можно показать, что его движение можно описать как примерно
равноускоренное. Чтобы уменьшить ускорение пустим этот шар по желобу,
наклоненному под некоторым углом к горизонту. Качение такого шара, попрежнему остается равноускоренным, но величина ускорения уменьшается по
мере уменьшения угла наклона. Поэтому разумно предположить, что при
движении по горизонтальному желобу ускорение станет равным нулю. Именно,
ускорение, а не скорость! Иными словами, его движение будет равномерным, с
постоянной скоростью. Конечно, со временем шар остановится, но его
торможение можно объяснить действием сил сопротивления воздуха и сил
трения.
Рассмотрим еще один пример. Толкнем шайбу по поверхности стола.
Сдвинувшись на некоторое расстояние, она остановится, следовательно, она
движется с уменьшающейся скоростью, с отрицательным ускорением. Заменим
поверхность стола, гладкой поверхность льда. И сообщим шайбе ту же
начальную скорость. В этом случае шайба пройдет до остановки гораздо
большее расстояние. Следовательно, величина (модуль) ее ускорения будет
1
Мерой действия одного тела на другое является сила - строгое физическое понятие. Однако,
пока мы будем использовать этот термин в обыденном житейском смысле.
2
На самом деле ситуация прямо противоположная - перед телом, движущимся в воздухе, среда
более плотная, чем сзади него, этим объясняется возникновение сил сопротивления.
40
меньше. Поэтому разумно считать, что причиной отрицательного ускорения
является сила сопротивления со стороны поверхности. Если каким-либо
образом исключить действие поверхности, то движение шайбы должно
продолжаться бесконечно долго.
Во всех случаях, оказывается можно найти причину изменения (!)
скорости - действие других тел.
Таким образом, можно утверждать, что при отсутствии воздействия
других тел, тело продолжает двигаться с постоянной скоростью, сохраняет
скорость своего движения. Свойство тел сохранять свою скорость называется
инерцией, а свободное движение тел называют движением по инерции.
Сформулированной утверждение в физике носит название закона инерции
Галилея.
Отметим, что, когда говорят о движении с постоянной скоростью,
подразумевают постоянство скорости, как по величине, так и по направлению.
Вспомните, как трудно повернуть на гладком льду - не хватает внешних сил,
способных изменить направление скорости.
Говоря в дальнейшем о
равномерном движении, мы будем подразумевать движение с постоянной
скоростью, как по величине, так и по направлению.
С проявлением инерции мы постоянно встречаем в окружающем мире.
При резком торможении автобуса, пассажиров «бросает» вперед - они
продолжают двигаться с прежней скоростью. Если на стол положить лист
бумаги, а на него поставить какой либо предмет, то можно резко выдернуть этот
лист бумаги так, что сам предмет не сдвинется с места.
В разделе «Кинематика»
мы неоднократно подчеркивали, что
механическое движение относительно - имеет смысл говорить только о
движении одного тела относительно другого. Поэтому, в формулировке закона
инерции Г.Галилея мы упустили одну существенную деталь – относительно
какой системы отсчета рассматривается движение. Не трудно привести пример
системы отсчета, в которой закон инерции не выполняется. Пусть поезд
начинает отходить ускоренно от вокзала, в системе отсчета, связанной с
поездом, вокзал движется с ускорением, хотя явных взаимодействий,
приводящих к изменению скорости вокзала не заметно.
Поэтому закону инерции Г.Галилея3 следует дать иную интерпретацию:
существуют такие системы отсчета, в которых тело движется равномерно,
если при отсутствии взаимодействия с другими телами. Такие системы
отсчета называются инерциальными.
Пусть некоторое тело А движется равномерно и прямолинейно
относительно некоторой системы отсчета XOY . В любой другой системе
отсчета, которая движется относительно XOY равномерно, движение тела А
будет равномерным (но, конечно, с другой скоростью). Следовательно, любая
система отсчета, которая движется равномерно относительно какой-нибудь
инерциальной системы отсчета, сама является инерциальной.
Вопрос о существовании инерциальных систем отсчета, на самом деле, не
простой. Во многих случаях, в качестве инерциальной системы отсчета рассматривают
систему отсчета, связанную с поверхностью земли. Строго говоря, эта система не
3
Перед самим Г. Галилеем такой проблемы не стояло, он был убежден в существовании
«абсолютного» движения. Более четко эта позиция была сформулирована И.Ньютоном:
существует некое «абсолютное пространство», которое существует само по себе, не зависимо от
существующих в нем материальных тел, поэтому абсолютное движение есть движение
относительно этого абсолютного пространства.
41
является инерциальной, так как Земля вращается вокруг собственной оси, то есть
движется с ускорением. Эта неинерциальность проявляется в целом ряде
экспериментов: движении маятника Фуко, отклонением в полете снарядов, подмыве
одного из берегов рек и других. Безусловно, эти эффекты малы, и при решении многих
задач ими можно пренебречь, то есть считать Землю инерциальной системой.
Аналогичные рассуждения можно применить и к другим более грандиозным системам,
например, связанным с Солнцем или другими звездами. Поэтому, вопрос об
инерциальности той или иной системы отсчета связан с той точностью, которая
требуется для описания физических явлений.
Таким образом, закон инерции постулирует существование
инерциальных систем отсчета. Далее, если не будет оговорено особо, мы будем
рассматривать движение тел именно в инерциальных системах отсчета.
4.2 Взаимодействие тел. Масса тела. Плотность. Сила.
Мы показали, что при отсутствии взаимодействия тела движутся
равномерно в инерциальных системах отсчета. Только действие одного тела на
другое приводит к изменению скорости его движения, к появлению ускорения.
Следовательно, ускорение тела служит показателем того, что тело подверглось
воздействию со стороны других тел. Однако, само ускорение не может служить
мерой взаимодействия тел, так как оно зависит не только от характеристик
взаимодействия, но и от свойств самого тела. Поэтому нам необходимо
определить от каких характеристик тела, и от каких характеристик
взаимодействия зависит величина ускорения.
Как мы отмечали, способность тела сохранять свою скорость называется
инерцией. Повседневный опыт убеждает нас, что труднее сдвинуть с места
более тяжелое тело. Точно также труднее остановить более тяжелое тело.
Следовательно, тяжелое тело является более инертным. Мерой инерции
является масса тела. Понятие массы нам хорошо знакомо, мы без труда
определяем массу тел с помощью весов, постоянно пользуемся знакомыми и
привычными единицами измерения массы - грамм, килограмм, тонна и т.д.
Массу тела интуитивно воспринимают4 как «количество вещества, материи»,
содержащейся в теле. Однако такое понимание является весьма упрощенным масса это характеристика инерционных свойств тела. Нужно дать строгое,
научное определение массы.
Многочисленные физические эксперименты и практический опыт
человека убеждают нас, при любом взаимодействии между двумя телами,
отношение ускорений, приобретаемых ими, не зависит от вида и величины
взаимодействия. Следовательно, отношение ускорений является величиной,
зависящей только от свойств самих тел - от их инерционных свойств.
Принято считать, что отношение ускорений, приобретаемых телами в
результате взаимодействия, обратно отношению масс тел
a1 m2
=
.
(1)
a2 m1
Именно это соотношение фактически является определением массы тела.
Если массу одного из тел взять в качестве эталона, то масса любого другого
может быть определена из соотношения (1)
a
(2)
m = m эт. эт. .
a
4
Именно так определял массу И. Ньютон.
42
Единицей массы в системе СИ является 1 килограмм.
Конечно, обычно массу тела измеряют другими способами, например,
взвешиванием. Но, строго говоря, при взвешивании мы измеряем не массу, силу
притяжения тела к земле, поэтому необходимы дополнительные доказательства
того, что эта сила пропорциональна массе тела. Эти доказательства мы
продемонстрируем позднее.
После того, как мы четко определили массу как меру инертности тел,
можно приступить к изучению характеристик взаимодействий тел. Для этого
нам надо каким-либо образом создать, хотя бы мысленно, устройство
обеспечивающее, постоянное воздействие на произвольное тело. В качестве
такого устройства можно, например, рассматривать пружину, сжатую на
определенную величину. Опыт показывает, что при одном и том же
воздействии на тело, произведение массы тела на приобретаемое ускорение
является постоянной величиной, не зависящей от самого тела, а полностью
определяемой видом воздействия. Следовательно, эта величина может
служить характеристикой воздействия одного тела на другое - эта
r
r
характеристика называется силой F = ma . Подчеркнем, что сила является
векторной величиной, ее направление совпадает с направлением ускорения,
которое приобретает тело. Изменение направление силы приводит к изменению
направление ускорения, вызванного этой силой.
Единицей измерения силы в системе СИ является ньютон. Сила в 1
ньютон сообщает телу массой 1 килограмм ускорение равное 1 метру в секунду
за секунду
[Н ] = [кг ] ⋅2[м]
с
Итак, теперь мы имеем возможность количественно изучать различные
виды взаимодействия - для этого у нас есть физическая величина- сила,
описывающая взаимодействие, есть единица ее измерения - Ньютон.
Вернемся еще раз к понятию массы тела. Конечно, не представляет
большой проблемы измерить массу тела, например, с помощью весов. Тем не
менее, масса тела в некоторых случаях может (и должна) быть рассчитана. В
таких ситуациях весьма полезным бывает понятие плотности вещества. Если
тело изготовлено из одного материала, то, очевидно, что его масса
пропорциональна объему тела. Поэтому отношение массы тела к его объему
является характеристикой вещества, из которого изготовлено тело – эта
характеристика называется плотностью вещества. Таким образом, плотность
вещества ρ есть отношение массы тела m , изготовленного из данного
вещества, к объему тела V
m
ρ= .
V
[ ]
В общем случае, когда тело не является однородным, следует ввести понятие средней
плотности в пределах некоторой части тела объемом ∆V ,
имеющей массу ∆m :
ρ ср. =
∆m
.
∆V
Эта характеристика усредняет инерционные
характеристики части тела. Если мы хотим с большей
точностью описать распределение масс в объеме тела, мы
должны вводить средние плотности для все более мелких
частей тела. В пределе, можно говорить о плотности тела, как функции координат его отдельной
43
бесконечно малой части, то есть рассматривать плотность как функцию координат выбранной
точки тела ρ ( x, y , z ) . Безусловно, что понятие плотности в данной точке с физической точки
зрения, по крайней мере, противоречиво. Массой может обладать только тело конечного объема
(хотя бы превышающего объем отдельной молекулы). Однако, с точки зрения простоты
математического описания, удобней рассматривать плотность неоднородного тела как функцию
координат ρ ( x, y, z ) , понимая, что физический смысл имеет только произведение
∆m = ρ ( x, y, z )∆V , приблизительно равное массе малой части тела объемом ∆V , если эта
часть включает точку с координатами ( x, y, z ) . Причем точность этой формулы тем выше, чем
меньше величина выделенного объема ∆V .
Если задать распределение плотности тела ρ ( x, y, z ) , то для вычисления суммарной
массы тела, необходимо применить следующую математическую процедуру: мысленно разбить
тело на малые части, объемы которых равны ∆Vi ( i = 1,2,3... - номер выделенной части тела),
подсчитать массы каждой части ∆mi =
ρ i ∆Vi , и вычислить массу тела как сумму масс всех
его частей
m = ∆m1 + ∆m 2 + ∆m3 + ... =
∑ ∆m = ∑ ρ ∆V .
i
i
i
i
(3)
i
4.3 Законы динамики Ньютона.
В 1723 году вышла книга английского ученого Исаака Ньютона
«Математические начала натуральной философии», в которой были
сформулирована система законов динамики, подобная системе аксиом
геометрии Эвклида. В отличие от математических аксиом законы физики
являются обобщением громадного числа физических экспериментов, также они
подтверждаются справедливостью многочисленных следствий применения этих
законов при описании механического движения. Тем не менее, с формальной
точки зрения их можно рассматривать именно как аксиомы, не следующие из
других более общих законов.
Три закона динамики И.Ньютона следует рассматривать в тесной
взаимосвязи, так как только в совокупности они составляют фундамент
динамики - науки, позволяющей описывать механическое движение, выяснять
причины изменения скоростей тел, объяснять и управлять этим движением.
Сразу подчеркнем, что знание только трех законов динамики не дает
возможности решить ни одной конкретной задачи – такие возможности
появляются только в том случае, когда они дополняются большим числом
других законов, дающим выражения для сил конкретных взаимодействий.
Законы динамики связывают ускорения тел с характеристиками тел
(массами) и их взаимодействий (силами), поэтому неудивительно, что в основу
динамики И. Ньютоном были положены именно три закона.
1 закон Ньютона. В качестве 1 закона Ньютоном был взят закон инерции Г.
Галилея, который был сформулирован и обоснован нами ранее: существуют
инерциальные системы отсчета, т.е. такие системы отсчета, в которых тело
движется равномерно и прямолинейно, если другие тела на него не
действуют. Основная роль этого закона – подчеркнуть, что в этих системах
отсчета
все ускорения, приобретаемые телами, являются следствиями
взаимодействий тел. Дальнейшее описание движения следует проводить только
в инерциальных системах отсчета.
2 закон Ньютона утверждает, что причиной ускорения тела является
взаимодействие тел, характеристикой которого является сила. Этот закон дает
основное уравнение динамики, позволяющее, в принципе, находить закон
44
движения тела, если известны, силы действующие на него. Этот закон может
быть сформулирован следующим образом (рис. 40):
Ускорение точечного тела (материальной точки) прямо
пропорционально сумме сил, действующих на тело, и обратно
пропорционально массе
r тела
r F
,
(1)
a=
m
r
здесь F - результирующая сила, то есть векторная сумма всех сил,
действующих на тело.
На первый взгляд, уравнение (1) является другой формой записи
определения силы, данного в предыдущем разделе. Однако, это не совсем так.
Во-первых, закон Ньютона утверждает, что в уравнение (1) входит сумма всех
сил, действующих на тело, чего нет в определении силы. Во-вторых, 2 закон
Ньютона однозначно подчеркивает, что сила является причиной ускорения тела,
а не наоборот.
Наконец, все физические величины определяются на основании частных
случаев тех или иных физических законов, так что 2 закон Ньютона не является
в этом случае исключением. С одной стороны, этот закон позволяет изучать
различные виды взаимодействий, т.е. экспериментально получать законы этих
взаимодействий. С другой стороны, при известных силах, этот закон дает
уравнение, позволяющее находить закон движения тела.
Так же подчеркнем, что первый закон не является следствием второго.
Формально, если сумма сил, действующих на тело равна нулю, то ускорение
тела равно нулю, то есть тело движется равномерно и прямолинейно. Однако,
напомним, что именно первый закон указывает те системы отсчета, в которых
выполняется второй закон.
3 закон Ньютона подчеркивает, что причиной ускорения является взаимное
действие тел друг на друга. Поэтому силы, действующие на
взаимодействующие тела,
являются характеристиками одно и того же
взаимодействия. С этой точки зрения нет ничего удивительного в третьем
законе Ньютона (рис. 41):
точечные
тела
(материальные
точки)
взаимодействуют с силами равными по величине и
противоположными
по
направлению
и
направленными вдоль прямой, соединяющей эти
тела:
r
r
F12 = − F21 ,
(2)
r
где F12 - сила, действующая на первое тело, со стороны
r
второго, а F21 - сила, действующая на второе тело, со стороны первого.
Очевидно, что эти силы имеют одинаковую природу. Этот закон также
является обобщением многочисленных экспериментальных фактов. Обратим
внимание, что фактически именно этот закон является основой определения
массы тел, данного в предыдущем разделе.
Сформулированные законы динамики играют роль своеобразных аксиом,
то есть утверждений, не выводимых из более общих физических законов.
Обратите внимание, что рассматриваемые законы сформулированы для
точечных тел (материальных точек). Их применение для реальных тел,
имеющих конечные размеры, требует уточнения и обоснования.
45
4.4 Поступательное движение твердого тела.
Мысленно разобьем произвольное твердое тело на столь малые части,
чтобы каждую из них можно было рассматривать как материальную точку, к
которым применимы три закона динамики И.Ньютона.
Рассмотрим
произвольную
систему
материальных
точек
(рис.
42),
которые
взаимодействуют между собой (эти силы назовем
внутренними) и с другими телами, не входящими
в рассматриваемую систему (внешние силы).
Пронумеруем эти точки. В соответствии со
вторым
законом
Ньютона
для
каждой
материальной точки (например, номер 1)
справедливо уравнение
r
r
r
r
r
m1 a1 = F1( вн ) + F12 + F13 + ... + F1k + ... ,
(1)
r
где m1 - масса рассматриваемой точки; a1 - ее
r r
r
ускорение; F12 , F13 ,...F1k - силы5, действующие на точку 1, со стороны
r
материальных точек 2,3,…k…; F1( вн ) - сумма внешних сил, действующих на
точку 1. Просуммируем уравнения вида (1) для всех точек, включенных в
рассматриваемую систему, в результате чего получим очень громоздкое
уравнение
r
r
r
r
r
r
r
m1 a1 + m2 a 2 + m3 a3 + ... = F1( вн ) + F12 + F13 + ... + F1k + ...
r
r
r
r
(2)
+ F2( вн ) + F21 + F23 + ... + F2 k + ... ,
r ( вн ) r
r
r
+ F3 + F31 + F32 + ... + F3k + ...
В этом уравнении силы взаимодействия между двумя материальными точками
взаимно уничтожаются (!), в соответствии с 3 законом Ньютона. Например,
r
r
r
r
r
F21 = − F12 , поэтому F21 + F12 = 0 . Таким образом, в правой части уравнения (2)
остается сумма только внешних сил, действующих на систему:
r
r
r
r
r
r
m1 a1 + m2 a 2 + m3 a3 + ... = F1( вн ) + F2( вн ) + F3( вн ) + ....
(3)
При поступательном движении твердого тела ускорения всех точек тела
r
r
r
r
a1 = a 2 = a3 = ... = a , поэтому уравнение (3) еще больше
одинаковы
упрощается и приобретает вид, совпадающий с уравнением 2 закона Ньютона
для материальной точки,
r
r F
(4)
a= ,
m
r
в котором F - сумма внешних сил, действующих на тело, m - масса тела.
Итак, при поступательном движении твердого тела, ускорение тела
пропорционально сумме внешних сил, действующих на тело и обратно
пропорционально массе тела.
Обратите внимание, что обоснование применимости уравнения второго
закона (4) к движению твердого тело потребовало также привлечения третьего
закона Ньютона.
5
Обращайте внимание на индексные обозначения сил взаимодействия: здесь первый индекс
указывает номер тела, на которое действует сила, со стороны тела, номер которого указывает
второй индекс. Некоторые авторы предпочитают противоположную индексацию.
46
4.5 Произвольное движение твердого тела и системы тел.
Рассмотрим теперь уравнение второго закона Ньютона для произвольной
системы материальных точек и их произвольного движения. Оказывается, что в
этом случае можно рассматривать движение некоторой геометрической точки,
для которой уравнение движения полностью определяется только внешними
силами. В качестве такой точки следует взять центр масс системы.
Пусть совокупность тел представлена набором материальных точек,
m1 , m2 , m3 ... ,
массы которых обозначим
положения этих точек определим с помощью
r r r
их радиус-векторов r1 , r2 , r3 ... в некоторой
системе координат XYZ (рис. 43). Радиусвектор центра масс системы определяется по
формуле
r
mi ri
r
r
r
m r + m2 r2 + m3 r3 + ...
r
(1)
= i
rC = 1 1
m1 + m2 + m3 + ...
mi
∑
∑
i
Аналогично можно выразить векторы скорости и ускорения центра масс
системы через соответствующие характеристики движения материальных точек
r
mi v i
r
r
r
r
m v + m2 v 2 + m3 v3 + ...
(2)
VC = 1 1
= i
m1 + m2 + m3 + ...
mi
∑
∑
r
ma
r
r
r
∑
m a + m a + m a + ...
=
=
m + m + m + ...
∑m
i
r
aC
i
1 1
2
1
2
2
3
3
i
3
i
(3)
i
i
В знаменателях этих формул стоит суммарная масса всей системы
m1 + m2 + m3 + ... = m . В числителе формулы (3) стоит тоже выражение, что и в
уравнении (3) раздела 4.4. Поэтому из этих соотношений следует простое
уравнение для ускорения центра масс:
для произвольной системы, независимо от того движутся ли части этой
системы друг относительно другаr или нет, ускорение центра масс системы
r
r
F
определяется уравнением aC = , в котором F - сумма внешних сил,
m
действующих на систему, m - масса всей системы.
Мы определили особую точку системы материальных точек – центр
масс. Фактически введение этого понятие оправдывается простой уравнения,
описывающего ее движение. Упрощенно можно сказать, что всю массу системы
можно собрать в центре масс и при этом рассматривать движение системы как
движение одной материальной точки. Существенно, что движение центра масс
полностью определяется внешними силами, и не зависит от внутренних сил,
действующих между отдельными телами, входящими в рассматриваемую
систему. Например, центр масс осколков, разорвавшегося в воздухе снаряда
продолжает двигаться по параболе (если, конечно пренебречь сопротивлением
воздуха), не зависимо от того, какие дополнительные скорости приобрели эти
осколки в момент разрыва.
47
Отметим, еще одно существенное обстоятельство: если в какой либо
инерциальной системе отсчета центр масс системы покоится, то никакие
внутренние силы не могут изменить его положение.
Для твердого тела, расстояния между точками которого остаются
неизменными, центр масс однозначно «привязан» к самому телу.
Рассмотрим простейший пример
твердого тела,
состоящего из двух
небольших шариков (материальных точек),
массы которых равны m1 и m2 , соединенных
жестким невесомым стержнем длиной l
(рис.44). Направим ось X вдоль стержня,
начало отсчета совместим с первым
шариком. Используя определение
(1),
следует, что центр масс находится на стрежне (координаты y, z обоих шариков
равны нулю, поэтому и соответствующие координаты центра масс также равны
нулю). Координата xC центра масс рассчитывается по формуле (с учетом
x1 = 0, x 2 = l )
m x + m2 x 2
m2
(4)
=
xC = 1 1
l.
m1 + m2
m1 + m2
Если массы шариков равны, то центр масс находится в середине стержня, если
масса одного из шариков значительно превышает массу другого, то центр масс
совпадает с массивным шариком. Так при m1 >> m2
xC = 0 , в противном
случае m1 << m2
xC = l . При произвольном соотношении между массами
шариков, центр масс находится ближе к более тяжелому шарику. Отметим
интересное соотношение, следующее из формулы (4),
m1l1 = m2 l 2 ,
где l1 , l 2 расстояния от центра масс до соответствующих материальных точек.
Для тел, простой геометрической
формы, их центр масс может быть легко
найден,
не
прибегая
к
громоздким
вычислениям по формуле
(1). Так для
однородного стержня центр масс находится в
его середине, для однородных кольца, диска,
шара
их
центр
масс
совпадает
с
геометрическим
центром.
Центр
масс
однородной
прямоугольной
пластинки
расположен в точке пересечения диагоналей,
для треугольной пластинки - в точке пересечения медиан. (Докажите эти
утверждения самостоятельно).
48
4.6 Вращательное движение твердого тела. Момент силы.
Конечно, положение одной, даже «особой», точки далеко не полностью
описывает движение всей рассматриваемой системы тел, но все-таки, лучше
знать положение хотя бы одной точки, чем не знать ничего. Тем не менее,
рассмотрим применение законов Ньютона к описанию вращения твердого тела
вокруг фиксированной оси6.
Начнем с простейшего случая: пусть материальная
точка массы m прикреплена с помощью невесомого
жесткого стержня длиной r к неподвижной оси OO' (рис.
46). Материальная точка может двигаться вокруг оси,
оставаясь
от
нее
на
постоянном
расстоянии,
следовательно, ее траектория будет являться окружностью
с центром на оси вращения.
Безусловно,
движение
точки
подчиняется
r r
уравнению второго закона Ньютона ma = F рез . Однако, непосредственное
применение этого уравнения не оправдано: во-первых, точка обладает одной
степенью свободы, поэтому в качестве единственной координаты удобно
использовать угол поворота, а не две декартовые координаты; во-вторых, на
рассматриваемую систему действуют силы реакции в оси вращения, а
непосредственно на материальную точку – сила натяжения стержня.
Нахождение этих сил представляет собой отдельную проблему, решение
которой излишне для описания вращения. Поэтому имеет смысл получить на
основании законов Ньютона специальное уравнение, непосредственно
описывающее вращательное движение.
Пусть в некоторый момент времени на
r
материальную точку действует некоторая сила F ,
лежащая в плоскости перпендикулярной оси вращения
(рис.
47).
При
кинематическом
описании
r
криволинейного движения вектор полного ускорения a
удобно разложить на две составляющих: нормальную
r
a n , направленную к оси вращения, и тангенциальную
r
aτ , направленную параллельно вектору скорости.
Значение нормального ускорения для определения
закона движения нам не нужно. Конечно, это ускорение также обусловлено
действующими силами, одна из которых неизвестная сила натяжения стержня.
Запишем уравнение второго закона в проекции на тангенциальное
направление:
maτ = Fτ ,
(1)
заметим, что сила реакции стержня не входит в это уравнение, так как она
направлена вдоль стержня и перпендикулярна выбранной проекции. Изменение
∆ϕ
угла поворота ϕ непосредственно определяется угловой скоростью ω =
,
∆t
6
В данном случае мы ограничиваемся рассмотрением вращения вокруг фиксированной оси,
потому, что описание произвольного вращательного движения тела представляет собой
сложную математическую проблему, далеко выходящую за рамки курса математики средней
школы. Знания же других физических законов, кроме рассматриваемых нами, это описание не
требует.
49
∆ω
.
∆t
Угловое ускорение связано с тангенциальной составляющей ускорения
соотношением aτ = rε . Если подставить это выражение в уравнение (9), то
получим уравнение, пригодное для определения углового ускорения. Удобно
ввести новую физическую величину, определяющую взаимодействие тел при их
повороте. Для этого умножим обе части уравнения (1) на r
(2)
mr 2 ε = Fτ r .
и рассмотрим выражение в его правой части Fτ r , имеющего смысл
произведения тангенциальной составляющей силы, на расстояние от оси
вращения до точки приложения силы. Это же
произведение можно представить несколько иной
форме (см. рис. 48) M = Fτ r = Fr cos α = Fd , здесь d расстояние от оси вращения до линии действия силы,
которое также называют плечом силы. Эта
физическая величина, произведение модуля силы на
расстояние от линии действия силы до оси
вращения (плечо силы) M = Fd
называется
моментом силы. Действие силы может приводить к
вращению, как по часовой стрелке, так и против
часовой стрелки. В соответствии с выбранным положительным направлением
вращения следует определять и знак момента силы. Заметьте, что момент силы
определяется той составляющей силы, которая перпендикулярна радиусвектору точки приложения. Составляющая вектора силы, направленная вдоль
отрезка, соединяющего точку приложения и ось вращения, не приводит к
раскручиванию тела. Эта составляющая при закрепленной оси компенсируется
силой реакции в оси, поэтому она не влияет на вращение тела.
Запишем еще одно полезное выражения для
r
момента силы. Пусть сила F приложена к точке А,
декартовые координаты которой равны x, y (рис. 49).
r
r r
Разложим силу F на две составляющие Fx , Fy ,
параллельные соответствующим Ося координат. Момент
r
силы F относительно оси, проходящей через начало
координат, очевидно равен сумме моментов составляющих
r r
Fx , Fy , то есть M = xFy − yFx .
изменение которой в свою очередь описывается угловым ускорением ε =
Аналогично, тому, как нами было введено понятие вектора угловой скорости, можно
определить также и понятие вектора момента силы. Модуль этого
вектора соответствует данному выше определению, направлен же
он перпендикулярно плоскости, содержащей вектор силы и
отрезок, соединяющий точку приложения силы с осью вращения.
Вектор момента силы также может быть определен как векторное
произведение радиус-вектора точки приложения силы на вектор
силы
r r r
M = r×F .
Заметим, что при смещении точки приложения силы вдоль линии ее
действия момент силы не изменяется.
Обозначим произведение массы материальной точки на квадрат
расстояния до оси вращения mr 2 = I (эта величина называется моментом
50
инерции материальной точки относительно оси). С использованием этих
обозначений уравнение (2) приобретает вид, формально совпадающий с
уравнением второго закона Ньютона для поступательного движения
Iε = M .
(3)
Это уравнение называется основным уравнением динамики вращательного
движения. Итак, момент силы во вращательном движении играет такую же
роль, как и сила в поступательном движении, именно он определяет изменение
угловой скорости. Оказывается, (и это подтверждает наш повседневный опыт)
влияние силы на скорость вращения определяет не только величина силы, но и
точка его приложения. Момент инерции определяет инерционные свойства
тела по отношению к вращению (говоря простым языком – показывает, легко ли
раскрутить тело) - чем дальше от оси вращения находится материальная точка,
тем труднее привести ее во вращение.
Уравнение (3) допускает обобщение на случай вращения произвольного
тела. При вращении тела вокруг фиксированной оси угловые ускорения всех
точек тела одинаковы. Поэтому, аналогично тому, как мы проделали при
выводе уравнения Ньютона для поступательного движения тела, можно
записать уравнения (3) для всех точек вращающегося тела и затем их
просуммировать. В результате мы получим уравнение, внешне совпадающее с
(3), в котором I - момент инерции всего тела, равный сумме моментов
составляющих его материальных точек, M - сумма моментов внешних сил,
действующих на тело.
Покажем, каким образом вычисляется момент
инерции тела. Важно подчеркнуть, момент инерции тела
зависит не только от массы, формы и размеров тела, но и от
положения и ориентации оси вращения.
Формально
процедура расчета сводится к разбиению тела на малые
части, которые можно считать материальными точками
(рис. 51), и суммированию моментов инерций этих
материальных точек, которые равны произведению массы
на квадрат расстояния до оси вращения
I = m1 r12 + m2 r22 + m3 r32 + ...
Для тел простой формы такие суммы давно подсчитаны, поэтому
часто достаточно вспомнить (или найти в справочнике)
соответствующую формулу для нужного момента инерции. В
качестве примера: момент инерции кругового однородного
цилиндра массы m и радиуса R для оси вращения совпадающей
1
с осью цилиндра равен I = mR 2 .
2
4.7 Статика – законы равновесия тел.
Рассмотрим, при каких условиях тело может находиться в состоянии
покоя, естественно, в какой либо инерциальной системе отсчета. На основании
законов динамики И.Ньютона можно сформулировать два обязательных
условия равновесия.
1. Векторная сумма внешних сил, действующих на тело, должна быть
равна нулю. Нами было показано, что ускорение центра масс тела полностью
определяется внешними силами, действующими на рассматриваемое тело. Если
эта сумма равна нулю, то ускорение центра масс тела равна нулю. Поэтому
51
можно выбрать такую систему отсчета, в которой центр масс покоится.
Заметим, что при вычислении суммы векторов, нас не интересуют точки
приложения различных сил, нам важны только величины и направления этих
сил. Поэтому, говорят, что при рассмотрении поступательного движения все
векторы сил можно переносить параллельно самому себе.
Так как центр масс твердого тела жестко связан с самим телом, то при
покоящемся центре масс, тело может только вращаться вокруг оси, проходящей
через центр масс. Для того, чтобы тело не начало вращаться необходимо,
выполнение второго условия равновесия.
2. Сумма моментов внешних сил, действующих на тело, должна быть равна
нулю. Согласно определению, момент силы зависит не только от величины и
направления этой силы, но и от оси вращения. Поэтому, говоря о покоящемся
теле, встает вопрос, относительно какой оси должны вычисляться моменты
действующих сил. Ответ на данный вопрос следующий – для покоящегося тела
суммарный момент равен нулю для любой мыслимой оси вращения! К счастью,
при рассмотрении условий равновесия нет необходимости рассматривать все
возможные оси вращения (что в принципе невозможно). Можно показать, что
если векторная сумма сил равна нулю и сумма моментов сил относительно
какой-либо оси равна нулю, то и сумма моментов сил относительно любой
другой параллельной оси также равна нулю.
Проиллюстрируем это положение простым примером. Пусть силы,
действующие на тело, лежат в одной плоскости и параллельны друг другу (рис.
53). Введем систему координат XOY , одна из осей которой X
перпендикулярна направлению действия сил и
проходит через ось вращения O . Обозначим
координаты точек приложения сил x1 , x 2 , x3 ,... ,
тогда суммарный момент сил относительно этой
оси равен
M = x1 F1 + x 2 F2 + x3 F3 + ... .
Вычислим момент сил относительно оси O' ,
отстоящей от оси O на расстоянии a
M ' = (x1 + a )F1 + ( x 2 + a )F2 + ( x3 + a )F3 + ... =
= x1 F1 + x 2 F2 + x3 F3 + ... + a(F1 + F2 + F3 + ...) =
= M + a(F1 + F2 + F3 + ...)
Как следует из полученного соотношения, при (F1 + F2 + F3 + ...) = 0
M ' = M . То есть, если сумма сил равна нулю, то суммарные моменты сил,
относительно всех параллельных осей, равны.
Практически важным является случай, когда не тело
действуют две силы, равные по величине и
противоположные по направлению, но приложенные к
разным точкам (в этом случае говорят о паре сил).
Момент пары сил не зависит от оси вращения и равен
M = aF (где F - модуль каждой силы, a - расстояние
между линиями действия сил).
52
§5. Виды взаимодействий.
Для описания движения тел рассмотренных законов Ньютона явно не достаточно.
Что бы получить систему уравнений, позволяющих находить законы движения, система
трех законов Ньютона дополняется значительной группой законов, определяющих
выражения для сил различных типов взаимодействий. Сам И. Ньютон опубликовал свой
основополагающий труд по основам динамики, только после того, как им был установлен
и обоснован закон гравитационного взаимодействия тел. Впоследствии экспериментально
были установлены законы для других видов сил – упругости, трения, электрических,
магнитных и так далее.
Развитие физики постоянно приводит к построению все более общих теорий, и в
настоящее время все виды взаимодействий сводятся к четырем фундаментальным1, к
числу которых относятся гравитационные, электромагнитные, слабые и сильные.
Последние два присущи взаимодействиям между элементарными частицами и в
классической физике не рассматриваются, так их описание возможно только в рамках
современных квантово-релятивистских представлений.
5.1 Гравитационные взаимодействия. Закон всемирного тяготения Ньютона.
Гравитационные взаимодействия присущи всем материальным телам.
Закон, описывающий эти силы, открытый И. Ньютоном и опубликованный в 1687 году,
получил название закона всемирного тяготения: две материальные точки
притягиваются с силами пропорциональными произведению масс этих точек,
обратно пропорциональными квадрату расстояния между точками и направленной
вдоль прямой, соединяющей эти точки:
mm
F = G 12 2 .
(1)
r
Так как сила является векторной
величиной, то и формуле, определяющей силу
притяжения, следует придать векторную форму.
r
Для этого введем вектор r12 , соединяющий точки
1
и 2 (рис.55). Тогда сила притяжения,
действующая на второе тело, может быть
записана в виде
r
mm r
F21 = −G r1 32 r12 .
(2)
r12
В формулах (1), (2) коэффициент пропорциональности, который называется
гравитационной постоянной. Значение этой величины не может быть найдено из других
физических законов и определено экспериментально.
Численное значение
гравитационной постоянной зависит от выбора системы единиц, так в системе СИ оно
м3
равно G = 6,6720 ⋅10 −11 2
.
с ⋅ кг
Вопрос о природе гравитационного взаимодействия является чрезвычайно сложным. Сам И.Ньютон
на этот вопрос давал лаконичный ответ: «Гипотез не измышляю», тем самым, отказываясь даже рассуждать
на эту тему. Достаточно того, что закон всемирного тяготения с высокой степенью точности количественно
описывает гравитационное взаимодействия. Громадные успехи ньютоновской механики почти на два
столетия предопределили подобный подход ко всей физической науке, не только механике: достаточно
открыть, найти законы, правильно описывающие физические явления, и научиться применять их к
количественному описанию этих явлений.
Так в изучении гравитации считалось, что непонятным образом одно тело может оказывать влияние
на другое, причем это влияние передается мгновенно, то есть изменение положения одного из тел
1
В течении нескольких десятилетий предпринимаются попытки объединить некоторые виды
взаимодействий.
53
мгновенно изменяет силы, действующие на другие тела, независимо от того, на каком расстоянии эти тела
расположены. Этот общий подход к характеру физических взаимодействий получил название теории
дальнодействия. Подобный взгляд на взаимодействия тел был распространен на электрические и
магнитные явления, изучение которых активно проводилось в течение 18 -19 веков. Лишь в 30-х годах 19
века английским физиком М.Фарадеем для электромагнитных взаимодействий были сформулированы
основные положения альтернативной теории близкодействия: для передачи взаимодействия обязательно
необходим «посредник», некая среда, передающая эти взаимодействия; сами взаимодействия не могут
передаваться мгновенно, требуется определенное время для того, чтобы изменение в положении одного из
тел «почувствовали» другие взаимодействующие тела. В начале 20 столетия немецкий физик А.Эйнштейн
построил новую теорию гравитации – общую теорию относительности. В рамках этой теории
гравитационные взаимодействия объясняются следующим образом: каждое тело, обладающее массой
изменяет свойства пространства-времени вокруг себя (создает гравитационное поле), другие же тела
движутся в этом измененном пространстве времени (в гравитационном поле), что приводит к появлению
наблюдаемых сил, ускорение и т.д. С этой точки зрения, выражение «находится в гравитационном поле»
эквивалентно выражению «действуют гравитационные силы».
К этим вопросам мы обратимся позднее при изучении электромагнитного поля.
Самое поразительное в явлении тяготения заключается в том, что гравитационные силы пропорциональны
массам тел. Действительно, ранее мы говорили о массе, как о мере инертности тела. Оказалось, что масса
также определяет принципиально иное свойство материальных тел – является мерой способности
участвовать в гравитационных взаимодействиях. Поэтому можно говорить о двух массах - инерционной и
гравитационной. Закон всемирного тяготения утверждает, что эти массы пропорциональны друг другу.
Подтверждением этого утверждения является давно известный факт – все тела падают на землю с
одинаковым ускорением. Экспериментально с высокой точностью пропорциональность гравитационной и
инерционной масс было подтверждено в работах венгерского физика Э. Лоранда. В последствии
пропорциональность инерционной и гравитационной масс легла в основу новой теории гравитации общей
теории относительности А. Эйнштейна.
В заключение отметим, что закон всемирного тяготения может быть положен в основу определения
единицы массы (конечно, гравитационной). Например: два точечных тела единичной гравитационной
массы, находящиеся на расстоянии в 1 метр, притягиваются с силой в 1Н.
Вопрос. Определите массы двух точечных тел, находящихся на расстоянии 1,0 м друг от
друга и взаимодействующих с силой 1,0 Н.
Для гравитационных сил справедлив принцип суперпозиции: сила, действующая
на точечное тело со стороны нескольких других тел, равна сумме сил действующих
со стороны каждого тела.
Это утверждение также является обобщением
экспериментальных данных и является фундаментальным свойством гравитационных
взаимодействий.
Посмотрим на принцип суперпозиции с математической точки зрения: по закону
всемирного тяготения сила гравитационного взаимодействия, пропорциональна массе
этих тела. Если бы зависимость от масс была не линейна, то и принцип суперпозиции не
выполнялся. Действительно, пусть тело массой m0 , взаимодействует с двумя точечными
телами массами m1 и m 2 . Поместим, мысленно тела m1 и m 2 в одну точку (тогда их
можно рассматривать как одно тело. В этом случае сила, действующее на тело m0 , равна
m (m + m )
mm
mm
F0 = G 0 1 2 2 = G 0 2 1 + G 0 2 2 и может быть представлена в виде суммы сил,
r
r
r
действующих со стороны двух тел m1 и m2 . В случае нелинейной зависимости между
силой и масса принцип суперпозиции был бы несправедлив.
Закон всемирного тяготения для точечных тел и принцип
суперпозиции позволяют, в принципе, вычислять силы
взаимодействия между телами конечных размеров. Для этого
необходимо мысленно разбить каждое из тел на малые участки,
каждый из которых можно рассматривать как материальную
точку. Затем вычислить двойную сумму сил взаимодействия
между всеми парами точек. В общем случае вычисление такой
суммы является сложной математической задачей.
Подчеркнем, что сила взаимодействия между телами конечных размеров
вычисляется только методом разбиения тел и последующего суммирования. Ошибочно
54
утверждение о том, что сила взаимодействия между телами может быть вычислена, как
сила взаимодействия равна силе взаимодействия точечных тел, расположенных в центрах
масс. Для обоснования этого утверждения рассмотрим простой пример.
Пусть одно из взаимодействующих тел
можно считать материальной точкой массы
m0 , а второе тело представимо в виде двух
материальных точек равных масс m ,
расположенных на фиксированном расстоянии
a друг от друга (рис. 57). Все материальные
точки расположены на одной прямой, расстояние от первого тела до центра второго
обозначим r . Сила притяжения, действующая на тело m0 , равна
F0 = G
mm0
+G
mm0
.
(3)
2
a⎞
a⎞
⎛
⎛
⎜r + ⎟
⎜r − ⎟
2⎠
2⎠
⎝
⎝
Если же соединить материальные точки, составляющие второе тело, в одну, массой 2m ,
расположенную в центре тела, то сила взаимодействия будет равна
2mm0
,
(4)
F '0 = G
r2
что отличается от выражения (3). Только при r >> a выражение (3) переходит в формулу
(2). Заметьте, что в этом случае второе тело следует рассматривать как материальную
точку.
2
Задание для самостоятельной работы.
1. При каком отношении a r погрешность формулы (4) (по сравнению с точным
выражением (3)) не превышает 1% ?
5.2 Сила тяжести.
Рассмотрим гравитационное взаимодействие между
однородной сферой радиуса R и массы M и
материальной точкой массы m , находящейся на
расстоянии r от центра сферы (рис. 58). В соответствии с
изложенной выше методикой расчета сил, необходимо
разбить сферу на малые участки и просуммировать силы,
действующие на материальную точку, со стороны всех
участков сферы. Такое суммирование впервые было
проведено И. Ньютоном. Не вдаваясь в математические тонкости проведенного расчета,
приведем окончательный результат: результирующая сила направлена к центру шара
Mm
(что вполне очевидно), а величина этой силы определяется формулой F = G 2 .
r
Иными словами, сила взаимодействия оказалась такой же, как сила взаимодействия
двух точечных тел, одно из которых помещено в центр сферы, и его масса равна массе
сферы. Существенным в этом расчете оказалось то обстоятельство, что сила
гравитационного взаимодействия обратно пропорциональна квадрату расстояния между
точечными телами, при любой другой зависимости силы от расстояния приведенный
результат расчета оказался бы не верным.
Полученный вывод очевидным образом обобщается на взаимодействие точечного
заряда и однородного шара. Для доказательства достаточно разбить шар на тонкие
сферические слои.
Аналогично можно показать, что сила гравитационного взаимодействия между
двумя сферически симметричными телами равна силе взаимодействия между
55
материальными точками таких же масс, расположенных в центрах тел. То есть при
расчете
гравитационного
взаимодействия
сферически
симметричные тела можно считать материальными точками,
расположенными в центрах этих тел, независимо от размеров
самих тел и расстояния между ними (рис. 59).
Применим полученные результат к силе, действующей на
все тела, находящиеся у поверхности Земли. Пусть тело, массой
m находится на высоте h над поверхностью Земли. С хорошей
точностью форму Земли можно считать шарообразной, поэтому
сила, действующая на тело, со стороны Земли направлена к ее
центру, а модуль этой силы выражается формулой
Mm
F =G
,
(1)
( R + h )2
где M - масса Земли, R - ее радиус. Известно, что средний радиус Земли равен
R ≈ 6350км . Если тело находится на небольших высотах по сравнению с радиусом Земли,
то высотой подъема тела можно пренебречь и в этом случае сила притяжения оказывается
равной
Mm
F = G 2 = mg ,
(2)
R
M
где обозначено g = G 2 - ускорение свободного падения. Гравитационная сила,
R
действующая на все тела у поверхности Земли, называется силой тяжести.
Векторы ускорения свободного падения в различных
точках не параллельны, так как направлены к центру
Земли. Однако если рассматривать точки, находящиеся
на небольшой по сравнению с радиусом Земли высоте,
то можно пренебречь различием
в направлениях
ускорения свободного падения и считать, что во всех
точках рассматриваемой области вблизи поверхности
Земли вектор ускорения постоянен как по величине, так
и по направлению (рис. 60).
В рамках такого
приближения, мы будем называть силу тяжести однородной.
Задания для самостоятельной работы.
1. Оцените, на какой высоте над поверхностью Земли ускорение свободного падения
уменьшается на 1%, по сравнению с ускорением на поверхности Земли.
2. На каком расстоянии у поверхности земли угол между векторами ускорений
свободного падения равен 1° ?
Строго говоря, модуль ускорения свободного падения различен в различных точках земной
поверхности. Эти различия обусловлены, во-первых, отличием формы Земли от шарообразной, во-вторых,
непостоянством плотности Земли. Заметим, что при определении ускорения свободного падения
необходимо принимать во внимание вращение Земли, которое приводит к уменьшению экспериментально
наблюдаемого значения ускорения по сравнению с формулой (5), кроме того, вращение Земли также
приводит к отклонению направления ускорения свободного падения, от направления на центр Земли. В
некоторых случаях эти поправки, связанные с вращением Земли включают в силу тяжести. Мы же, однако,
предпочитаем называть силой тяжести, только ту силу, которая вызвана гравитационным взаимодействием,
а экспериментально наблюдаемые малые поправки к законам движения, вызванные вращением Земли,
рассматривать отдельно, тем более, что они малы и очень часто ими можно пренебречь.
Сила тяжести, действующая на тело, является суммой сил, действующей на его
отдельные части. Если считать силу тяжести однородной, то суммарная сила тяжести,
действующая на тело равна произведению массы всего тела на ускорение свободного
падения. Более сложным является вопрос и точки приложения силы тяжести. По своей
56
природе сила тяжести является распределенной, действующей на все части тела. Если нас
интересует только величина суммарной силы тяжести, то ее точка приложения нас не
интересует. Однако во многих случаях (например, при исследовании условий равновесия)
нас интересует не только сама сила, но и ее момент. Можно выбрать такую точку
приложения суммарной силы тяжести, чтобы ее момент был равен сумме моментов сил
тяжести, действующей на отдельные части тела. Такая точка называется центром
тяжести тела.
Очередной раз мысленно разобьем тело массой m
на
малые
части,
массы
которых
обозначим
∆mi (i = 1,2,3...) . Выберем такую точку C приложения
суммарной силы тяжести mg , чтобы момент этой силы
относительно произвольной оси O был равен сумме
моментов сил тяжести, действующие на отдельные части
∆mi (i = 1,2,3...) , что математически выражается виде
тождества
mgxC = ∆m1 gx1 + ∆m2 gx 2 + ∆m2 gx 2 + ... ,
где x1 , x 2 , x3 ... - горизонтальные координаты частей тела, xC - горизонтальная координата
искомой точки приложения суммарной силы тяжести. Из данного выражения определяем
координату центра тяжести
∆mi xi
∆m1 x1 + ∆m2 x 2 + ∆m2 x 2 + ...
i
xC =
=
.
m
m
Таким образом, если вектор ускорения свободного падения принимается постоянным, то
центр тяжести совпадает с центром масс тела. Отметим, что в общем случае, когда вектор
ускорения по величине или направлению изменяется от точки к точке, центр тяжести
может отличаться от центра масс.
∑
5.3 Силы упругости. Закон Гука.
Само существование жидких и твердых тел свидетельствует о наличии сил
взаимодействия между молекулами. Эти силы определяются электромагнитными
взаимодействиями между движущимися заряженными частицами, из которых состоят
атомы и молекулы (электронами и ядрами). Теоретический расчет этих сил чрезвычайно
сложен, и в общем виде эта задача не решена до настоящего времени. Однако, можно
утверждать, что эти силы могут быть как силами притяжения (без сил притяжения все
молекулы бы разлетелись из-за их теплового движения), так и силами отталкивания (без
которых бы все тела сжались в одну точку). Равновесному положению молекул в
жидкости и твердом теле соответствует равенство сил притяжения и отталкивания. При
деформации тел (как жидких, так и твердых) равновесные расстояния между молекулами
изменяются, поэтому возникают силы, стремящиеся вернуть их в исходное состояние. Эти
силы проявляются как силы упругости. Отметим, что силы упругости не относятся к
фундаментальным, законы позволяющие вычислять их значения, как правило, являются
экспериментальными и выполняются приближенно.
В общем случае зависимость сил упругости от деформации может быть очень
сложной, однако при малых деформации справедлив закон Р.Гука: сила упругости
пропорциональна деформации тела и направлена в сторону противоположную
деформации. В простейшем случае деформации растяжения и сжатия закон Р. Гука
выражается формулой
Fупр. = −kx ,
(1)
57
где x - изменение длины тела, k - коэффициент пропорциональности (так же называемый
коэффициентом упругости), зависящий от материала тела, его размеров и формы. Знак
минус явно указывает, что сила упругости направлена в сторону, противоположную
деформации. Особенно хорошо этот закон выполняется для длинных пружин.
Всякий физический закон помимо чисто формальной связи между физическими
величинами, выражает также и причинно-следственные связи. По этому поводу в связи с
силами упругости необходимо высказать следующее замечание. Для того чтобы
деформировать тело, к нему необходимо приложить внешнюю силу,
тогда возникающие деформации приведут к появлению сил упругости
(рис. 62). Итак, причиной деформаций являются внешние воздействия,
а сами деформации являются причиной сил упругости. Если
деформированное тело находится в состоянии равновесия, то
r
возникающая сила упругости Fупр. оказывается равной по величине и
r
противоположной по направлению внешней силе F . Таким образом,
r
r
соотношение Fупр. = − F справедливо только в состоянии равновесия и
является следствием условий равновесия, а не 3 закона Ньютона, как
это иногда легкомысленно утверждается. Соотношение между силой
упругости и деформацией справедливо независимо от того, находится ли тело в состоянии
равновесия.
Если к твердому телу приложена внешняя сила,
направленная перпендикулярно его поверхности (нормально),
то возникающая деформация будет сжатием или растяжением.
Если к твердому телу приложить силу, направленную
параллельно
его
поверхности
(тангенциально),
то
возникающая деформация является сдвигом. В обоих случаях
возникающая сила упругости направлена в сторону,
противоположную внешней силе (рис. 63).
Рассмотренные в данном разделе законы являются приближенными, так при
больших деформациях нарушается пропорциональность между силами упругости и
деформациями. Кроме того, во многих случаях тело может не восстанавливать свою
форму после снятия нагрузки, такие деформации называются пластическими. Описание
сил упругости в таких ситуациях является весьма сложным, мы познакомимся с ним в
следующем году, после подробного изучения свойств твердых тел.
Силы упругости возникают, как в твердых телах, так и в жидкостях и газах. Для
жидких тел имеет смысл говорить только о нормальной силе, так как тангенциальные
силы приведут к перетеканию жидкости. Вспомните: «твердые тела сохраняют свою
форму и объем, а жидкости ее не сохраняют». Поэтому говорят, что в жидкостях
отсутствуют тангенциальные силы упругости. Такие свойства жидкости обусловлены ее
молекулярным строением: силы взаимодействия между молекулами проявляются только
при изменении расстояния между молекулами, сдвиг одной молекулы относительно
другой не приводит к появлению дополнительного взаимодействия. Отметим, что силы
упругости жидкости могут быть направлены как внутрь, так и наружу от жидкости, то
есть, жидкость может быть, как сжата, так и растянута. Так как жидкости при отсутствии
внешних воздействий сохраняют свой объем, то существует равновесное расстояние
между молекулами, при котором сила их взаимодействия равна нулю. При уменьшении
равновесного объема расстояния между молекулами меньше равновесных, поэтому между
молекулами начинают возникать силы отталкивания, в противном случае увеличения
объема расстояния между молекулами превышают равновесные, поэтому начинают
проявляться силы притяжения.
Пусть жидкость находится в сосуде под поршнем. Если к поршню приложить силу,
направленную наружу от жидкости, то благодаря силам притяжения между молекулами
58
жидкости, а также жидкости и поршня, жидкость окажется растянутой,
вследствие чего, появятся силы упругости, направленные внутрь жидкости
(рис. 64). Большинство жидкостей деформируются чрезвычайно мало, то
есть для того, чтобы получить заметную деформацию необходимо
приложить значительные внешние силы, и, наоборот – малые деформации
жидкости приводят к возникновению больших сил упругости. Во многих
случаях связь между деформациями и силами упругости жидкостей может
считаться линейной, соответствующей закону Гука.
Газы, в отличие от твердых тел и жидкостей не обладают
собственным объемом, полностью занимая весь сосуд, в котором они
находятся. Поэтому говорить о деформации газа не имеет смысла. Тем не менее, газы
оказывают давление на стенки сосуда, поэтому можно говорить об упругости газов.
Формально, можно считать, что собственный равновесный объем газа равен
бесконечности, поэтому при любом конечном объеме газ является сжатым. Зависимость
давления газа от его объема носит более сложный характер, чем закон Гука, и будет
изучаться нами позднее.
5.4 Силы реакции.
При соприкосновении тел, эти тела могут деформироваться. Часто эти деформации
могут быть чрезвычайно малыми, но, тем не менее, они приводят к возникновению сил
упругости, которые в этом случае называются силами реакции. Как и все силы
упругости, силы реакции направлены в сторону, противоположную возникшим
деформациям. Если два тела могут скользить одно по другому без трения2, то такие тела
называют гладкими. Для гладких поверхностей сила их взаимодействия направлена
перпендикулярно поверхности их соприкосновения и называется силой нормальной
реакции. Непосредственное вычисление сил реакции, как проявление сил упругости
затруднительно: для этого необходимо рассчитать деформации каждого тела, приводящие
к возникновению равновесных сил упругости. В связи с этим при решении различных
задач, силы реакции, как правило, находят из условий равновесия или законов движения
тел.
Рассмотрим простейшую ситуацию – твердый брусок массы m
расположен на твердой горизонтальной поверхности (рис. 65). Под
r
действием силы тяжести mg брусок крайне незначительно начнет
опускаться вниз, что приведет к незначительным деформациям, как
самого бруска, так и поверхности. В результате появятся силы
упругости бруска и поверхности. Этот процесс будет продолжаться до
тех пор, пока сила упругости, действующая со стороны поверхности на
r
брусок (то есть сила нормальной реакции) N не уравновесит силу
тяжести. Таким образом, в положении равновесия сила нормальной
реакции оказывается равной по величине и противоположно
r
r
направленной силе тяжести N = − mg . Опять подчеркнем, что этот вывод сделан на
основании 2 закона Ньютона. На основании третьего закона Ньютона можно утверждать:
первое, сила тяжести, равна силе, с которой брусок притягивает Землю; второе, сила
r
упругости (реакции) N , действующая на брусок со стороны поверхности, равна по
r
величине и противоположна силе упругости N ′ , с которой брусок действует на
r
r
поверхность N = − N ′ . Встречающееся в некоторых неудачных учебных пособиях
2
Конечно, такая ситуация является идеализацией, точнее надо говорить о возможности пренебрежения
силами трения.
59
r
утверждение о том, что на поверхность действует сила тяжести бруска mg , является
бессмысленным.
Аналогичные рассуждения можно провести для сил, действующих на
r
подвешенное тело. В этом случае сила тяжести mg , действующая на тело,
r
уравновешивается силой упругости (называемой также силой натяжения) T ,
возникающей в подвесе при его деформации (рис. 66).
Во многих случаях деформации опоры или подвеса являются настолько
малыми, что ими можно пренебречь, однако, следует помнить, что именно эти
деформации являются причиной возникновения сил реакции. Иными словами,
мы встречаемся с ситуацией «пренебречь можно – объяснить нельзя».
Сделаем несколько замечаний связанных с понятием веса тела. Наиболее популярное определение
этой физической величины следующее: вес тела, это сила, с которой тело действует на горизонтальную
опору или вертикальный подвес вследствие притяжения к Земле. При таком определении сила веса ничем
не отличается от силы реакции опоры и подвеса, поэтому введение дополнительного этого понятия является
излишним. Понятие веса тела может быть оправдано с физиологической точки зрения. Дело в том, что
человек и другие живые существа ощущают собственный вес, как силы воздействия одних внутренних
органов на другие. Именно с этими ощущениями связаны понятия перегрузки и невесомости. В
дальнейшем мы не будем пользоваться понятием веса тела.
5.5 Силы сухого трения.
Еще одним проявлением межмолекулярных взаимодействий являются силы
трения скольжения – силы, возникающие при относительном движении двух тел и
направленные вдоль границы их соприкосновения.
Одна из причин появления трения очевидна –
поверхности взаимодействующих тел не являются
идеально гладкими, микроскопические выступы и впадины
зацепляются друг за друга, в них возникают силы
упругости,
направленные
вдоль
поверхности
соприкосновения (рис. 67).
Однако только эта причина не объясняет всех
свойств и характеристик трения. В частности для
большинства веществ улучшение полировки поверхностей приводит не к уменьшению, а
увеличению трения. Для шероховатых поверхностей площадь реального контакта, где
действуют межмолекулярные силы прилипания, не велика (эти участки располагаются в
районах выступов), при полировке поверхностей площади этих областей увеличиваются,
что и приводит к увеличению сил трения. Рассматриваемое здесь явление называют также
сухим трением.
Следует отметить, что законченная теория сил сухого трения до настоящего
времени не построена. Поэтому законы, описывающие рассматриваемый вид
взаимодействия носят экспериментальный (эмпирический) характер. Наиболее простой
вид закона, описывающего силу трения скольжения, установлен экспериментально и
носит название закона Кулона-Амонтона. Это закон утверждает,
что сила трения скольжения пропорциональна силе
нормальной реакции3 взаимодействующих тел и направлена в
сторону,
противоположную
скорости
относительного
движения тел (рис.68)
(1)
Fтр. = µN ,
безразмерный коэффициент пропорциональности (называемый
коэффициент трения) µ зависит от материала соприкасающихся поверхностей и степени
их обработки. Как правило, этот коэффициент определяется экспериментально. Как уже
r
r
Заметим, что записывать этот закон в векторной форме F = − µN , как это делается в некоторых
справочниках, недопустимо, так силы нормальной реакции и трения взаимно перпендикулярны.
3
60
было отмечено, закон Кулона-Амонтона приближенный – так коэффициент трения может
незначительно зависеть от скорости, причем, как правило, с ростом скорости
коэффициент трения незначительно уменьшается. Из приведенного закона следует, что
сила трения не зависит от площади соприкасающихся тел, экспериментально же, такая
зависимость иногда наблюдается. Однако эти указанные особенности незначительно
влияют на величину силы трения, поэтому чаще ими пренебрегают и пользуются
приближенной формулой (1). Подчеркнем, что как любая другая сила, сила трения
является характеристикой взаимодействия тел, поэтому в соответствии с 3 законом
Ньютона, следует говорить о силах трения действующих на каждое из соприкасающихся
тел.
В заключение укажем еще одну интерпретацию
коэффициента сухого трения. При движении одного тела по
r
поверхности другого суммарная сила взаимодействия тел F реак .
r
r
разлагается на силу нормальной реакции N и силу трения Fтр. (рис.
69). Если величина силы трения определяется формулой (1), то угол
α между суммарной силой реакции и нормалью к поверхности
удовлетворяет условию tgα = µ .
Сила трения может возникнуть и в том случае, когда тела не движутся друг
относительно друга, такую силу называют силой трения покоя. Повседневный опыт
указывает, что для того чтобы сдвинуть одно тело относительно другого, необходимо
приложить силу, превышающую определенное пороговое значение (вспомните, например,
свои опыты по перетаскиванию мебели). Если же к телу приложить силу меньшую, то
r
тело остается в покое, следовательно, эта приложенная сила F компенсируется равной ей
силой трения покоя. Таким образом, сила трения покоя может принимать максимальное
значение, после чего трение покоя переходит в терние скольжения. Приближенно можно
считать, что максимальная сила трения покоя равна силе трения скольжения и
определяется формулой (7). Однако, как правило, максимальная сила трения покоя
превышает силу трения скольжения на 10%-20%., поэтому в некоторых случаях вводят
коэффициент трения покоя, незначительно превышающих коэффициент трения покоя. В
дальнейшем, этим различием мы будем пренебрегать.
Рассмотрим подробнее простую ситуацию: на
горизонтальной поверхности расположен небольшой брусок, к
которому
прикладывают
внешнюю
горизонтально
r
направленную силу F (рис.70). Действующая на брусок сила
r
тяжести mg приводит к незначительной деформации
r
поверхности, что вызывает появление силы реакции N . Если
r
горизонтальная сила F не превышает по модулю
максимально возможной силы трения покоя µN , то сила
трения (покоя) численно равна приложенной силе и
направлена в противоположную сторону, как только
r
модуль силы F превысит значение µN , начнется
скольжение бруска, при котором сила трения будет
оставаться приблизительно постоянной. Аналогичная
ситуация будет наблюдаться при изменении направления
действия внешней силы. Таким образом, график
зависимости проекции силы трения от внешней
приложенной силы имеет вид, показанный на рисунке 71.
61
Силы, препятствующие движению, наблюдаются и при качении одного тела по
поверхности другого. Эти силы называются силами трения качения. Сразу подчеркнем,
что природа этих сил отличается от сил сухого трения. Основной причиной
возникновения трения качения являются неупругие деформации самого катящегося тела и
поверхности, по которой происходит качение.
Так
колесо,
расположенное
на
горизонтальной
поверхности деформирует последнюю. При движении колеса
деформации не успевают восстановиться, поэтому колесу,
приходится, как бы все время взбираться на небольшую горку, изза чего появляется момент сил, тормозящий качение (рис. 72).
Неупругие деформации колеса также приводят к появлению
тормозящих сил.
Таким образом, силы трения качения определяются упругими свойствами
взаимодействующих тел. Закон для силы трения также является экспериментальным и
приближенным, его принято записывать в форме
k
Fтр.кач. = N ,
(2)
R
где N - сила нормальной реакции, R - радиус катящегося тела, k - коэффициент трения
качения, имеющий размерность длины. При записи формулы в такой форме, коэффициент
трения качения определяется, главным образом, материалом взаимодействующих тел и не
зависит от радиуса катящегося тела. Заметим, что для одних и тех же тел трение качения,
как правило, во много раз меньше трения скольжения, что вам хорошо известно из
повседневного опыта.
5.6 Силы вязкого трения.
Хорошо известно, что для уменьшения трения применяют различного вида смазки.
В этом случае между трущимися твердыми поверхностями образуется жидкая прослойка4.
Как уже было сказано ранее, в жидкостях отсутствуют тангенциальные механические
напряжения, что и является основной причиной уменьшения сил трения.
При относительном движении одного твердого
тела со скоростью V0 по смазанной поверхности второго
(которую считаем неподвижной), жидкость в прослойке
также приходит в движение. Причем скорости различных
слоев прослойки различны – они плавно изменяются от
V0 до нуля. При относительном движении слоев
жидкости между ними возникают силы вязкого трения,
также
обусловленные
межмолекулярными
взаимодействиями. Различия в скоростях граничащих слоев жидкости приводит к
возникновению сил, направленных вдоль границы раздела рассматриваемых слоев.
Величины этих сил зависят от свойств жидкости, толщины жидкого слоя и скорости
V0 результирующая сила трения
движущегося тела. При небольших скоростях
оказывается пропорциональной скорости тела и направленной в сторону
противоположную скорости, то есть может быть записана в векторной форме
r
r
F = − βV 0 ,
(1)
где β - коэффициент пропорциональности, зависящий от свойств жидкой прослойки и
толщины жидкого слоя.
4
Возможен промежуточный вариант – при малой толщине прослойки, могут оставаться небольшие области
непосредственного контакта твердых поверхностей.
62
При движении тела в жидкой или газообразной среде благодаря межмолекулярным
взаимодействиям прилегающие к телу слои жидкости или газа также приходят в
движение.
Причем скорости различных слоев оказываются различными, что также приводит к
появлению сил сопротивления. В общем случае вид зависимости силы сопротивления от
скорости может быть различным, однако,
при малых скоростях сила сопротивления
оказывается пропорциональной скорости,
то есть описывается формулой (9).
Вычисление
сил
сопротивления,
действующих на движущиеся тела, требует
расчета характера обтекания жидкости
вокруг тела (рис. 74), что представляет
собой очень сложную математическую
задачу.
При больших скоростях основной причиной возникновения сил сопротивления
оказываются столкновения частиц среды с движущимся телом. В этом случае сила
сопротивления оказывается приблизительно пропорциональной квадрату скорости
движения тела относительно жидкости
F = β 2v 2 .
К несколько более подробному теоретическому обоснованию этой формулы мы вернемся
чуть позднее.
63
§6. Законы сохранения в механике.
В предыдущих параграфах мы фактически построили общую схему решения
основной задачи динамики:
- целый ряд физических законов дают возможность рассчитывать силы, действующие на
тела;
- второй закон Ньютона и известные силы позволяют получить уравнения, для
определения ускорений тел;
- методы кинематики позволяют, в принципе, рассчитать законы движения тел, по их
известным ускорениям.
В данном параграфе мы рассмотрим фундаментальные физические законы
сохранения энергии, импульса и момента импульса, также позволяющие получать
уравнения для описания движения тел. Хотя эти законы нами будут получены на
основании законов Ньютона, их обобщения имеют большую область применения,
фактически именно законы сохранения являются фундаментом современной физики. В
некоторых случаях в качестве исходных аксиом механики (и других разделов физики)
используют законы сохранения, тогда законы Ньютона могут рассматриваться как
«теоремы», являющиеся следствием законов сохранения.
Рассматриваемые ниже законы сохранения тесно связаны со свойствами симметрии пространства и
времени. Симметрия в данном случае понимается в предельно широком смысле – наличие преобразований,
оставляющих все свойства рассматриваемой системы неизменными. Согласно знаменитой теореме Эмми
Нетер каждой сохраняющейся величине соответствуют некоторая симметрия, и наоборот наличие любого
элемента симметрии приводит к появлению сохраняющейся физической величины
6.1 Импульс тела. Закон сохранения импульса.
Уравнение 2 закона Ньютона для материальной точки (или для твердого тела,
движущегося поступательно) имеет вид
r r
ma = F ,
(1)
r
r
r ∆v
здесь m - масса тела, a =
- ее ускорение, F - сумма внешних сил, действующих на
∆t
тело. Используя определение ускорения, уравнение (1) можно переписать в виде
r
∆(mv ) r
= F . Векторная величина равная произведению массы тела на его скорость
∆t
r
r
p = mv называется импульсом тела1. Тогда второй закон Ньютона может быть
переформулирован следующим образом2: скорость изменения импульса тела равна
сумме внешних сил, действующих на тело
r
∆p r
=F.
(2)
∆t
На первый взгляд, эта новая формулировка закона полностью эквивалентна
прежней. Но, она оказывается применимой в том случае, когда масса тела изменяется с
течением времени.
Данный вывод, не может быть подтвержден какими-либо
теоретическими выкладками, обосновывается оно только результатами многочисленных
экспериментов и экспериментально проверяемыми следствия из данного утверждения.
Иными словами, уравнение (2) является обобщением экспериментальных данных.
В случае постоянной массы уравнения (2) и (1) полностью эквивалентны.
r
Часто произведение силы, на время ее действия F∆t называют импульсом силы.
Используя это понятие, дадим еще одну эквивалентную формулировку второго закона
1
Также эту физическую величину называют количеством движения, однако, этот термин постепенно
выходит из употребления.
2
Заметим, что именно в такой форме закон был сформулирован И.Ньютоном.
64
Ньютона: изменение импульса тела равно импульсу суммарной внешней силы
r r
∆p = F∆t .
Рассмотрим теперь движение двух материальных точек,
взаимодействующих только между собой (рис. 75), такую
систему можно назвать изолированной, в том смысле, что нет
взаимодействия с другими телами. По третьему закону Ньютона
силы, действующие на эти тела,
равны по величине и
r
r
противоположны по направлению F12 = − F21 . Эти можно
выразить, используя второй закон Ньютона
r
r
r
r
F12 = m1 a1 , F21 = m2 a 2 .
Объединяя эти выражения, получим
r
r
r
m1 a1 + m2 a 2 = 0 .
Перепишем данное соотношение, используя понятие импульса:
r
r
r
r
r
r
r
∆v1 ∆(m1v1 ) ∆p1
∆p1 ∆p 2 r
∆( p1 + p 2 ) r
r
m1 a1 = m1
=
=
. Следовательно,
+
= 0 , или
= 0 . Если
∆t
∆t
∆t
∆t
∆t
∆t
изменение какой-либо величины равно нулю, то эта физическая величина сохраняется.
Таким образом, приходим к выводу: сумма импульсов двух взаимодействующих
изолированных точек остается постоянным, независимо от вида взаимодействия
между ними. Этот вывод можно обобщить на произвольную изолированную систему
материальных точек, взаимодействующих между собой.
Ранее в качестве одного из следствий законов Ньютона, мы получили уравнение,
описывающее движение центра масс системы материальных точек
r
r
ma C = F ,
(3)
r
r
где m - полная масса системы, aC - ускорение центра масс системы, F - сумма внешних
сил, действующих на систему, если система изолирована, то сумма внешних сил равна
r
r
нулю, поэтому в таком случае ma C = 0 . Вспомним определение центра масс системы.
Радиус-вектор центра масс определяется по формуле
r
r
r
m1 r1 + m2 r2 + m3 r3 + ...
r
rC =
.
m1 + m2 + m3 + ...
r
Тогда произведение maC можно представить в виде
r
r
r
∆v3
∆v1
∆v 2
r
r
r
r
(m1 + m2 + m3 + ...)aC = m1a1 + m2 a 2 + m3 a3 + ... = m1
+ m2
+ m3
+ ...
∆t
∆t
∆t
,
(4)
r
r
r
r
∆(m1v1 + m2 v 2 + m3 v3 + ...) ∆P r
=
=
=0
∆t
∆t
r
r
r
r
где P = m1v1 + m2 v 2 + m3 v3 + ... - векторная сумма импульсов тел, входящих в систему,
которую в дальнейшем будет называть импульс системы. Из полученного соотношения
следует, что полный импульс замкнутой системы сохраняется, независимо от видов
взаимодействий внутри системы. Это чрезвычайно важное утверждение носит название
закона сохранения импульса.
Сделаем, два существенных замечания, касающихся проделанного вывода.
1. Полный импульс системы материальных точек равен произведению массы системы на
скорость центра масс системы. Действительно,
r
r
r
r
r
m1v1 + m2 v 2 + m3 v3 + ...
r
r
r
= mVC .
P = m1v1 + m2 v 2 + m3 v3 + ... = m
m1 + m2 + m3
2. Пусть система материальных точек не является замкнутой. Допустим, что сумма
r r
внешних сил действующих на систему не равна нулю F ≠ 0 , но проекция
65
результирующей внешней силы на некоторую ось (например, X ) равна нулю FX = 0 .
Тогда уравнение (3) в проекции на эту ось будет иметь вид maCX = 0 , из которого следует,
что проекция импульса системы на эту ось будет сохраняться. Итак, если сумма
проекций внешних сил на некоторую ось равна нулю, то проекция импульса
системы на эту ось сохраняется.
Так при движении системы материальных точек движет в поле тяжести земли,
когда внешней силой является сила тяжести, направленная вертикально, будет
сохраняться проекция импульса системы на любую горизонтальную ось.
Мы вывели закон сохранения импульса с помощью законов динамики Ньютона. Однако закон
сохранения импульса является фундаментальным физическим законом. В теоретической физике показано,
что он является следствием однородности3 пространства, в котором происходят все физические явления.
Если вы уверены в том, что результаты физического эксперимента одинаковы, независимо от того в каком
месте этот опыт поставлен, то вы должны признать закон сохранения импульса.
Задания для самостоятельной работы.
1. Движущийся кусок пластилина ударяется в стену и прилипает к ней. Куда «исчезает»
импульс куска пластилина?
6.2 Закон сохранения момента импульса.
Основное уравнение динамики вращательного движения совпадает с уравнением
второго закона Ньютона для поступательного движения. Поэтому для описания
вращательного движения можно провести аналогичные обобщения, приведшие нас к
закону сохранения импульса.
Уравнение динамики вращательного движения тела вокруг неподвижной оси
Iε = M ,
(1)
∆ω
(где ε =
- угловое ускорение тела, I - его момент инерции, M - сумма моментов
∆t
внешних сил, действующих на тело) перепишем в виде
∆(Iω )
=M.
(2)
∆t
Физическая величина L = Iω - называется моментом импульса. Уравнение (2)
оказывается применимым и для описания вращения тел, момент инерции которых
изменяется в процессе движения, поэтому имеет более широкую область применимости,
чем уравнение (1). Теперь основное уравнение динамики формулируется в виде: скорость
изменения момента импульса тела равна суммарному моменту сил, действующему
на тело. Доказать теоретически это утверждение невозможно – мы провели обобщение,
которое подтверждается многочисленными экспериментами.
Введенное нами определение момента импульса L = Iω
является частным случаем для этой физической величины.
Дадим еще одно определение этой физической величины.
Пусть материальная точка массы m движется со скоростью
r
r
r
v . Импульсом тела называется векторная величина p = mv .
Моментом импульса называется произведение импульса тела
на плечо импульса (расстояние от оси вращения до прямой,
вдоль которой направлен импульс)
L = mv ⋅ d .
(3)
Это определение аналогично определению момента силы.
Можно дать эквивалентные выражения формулы (3): L = mv ⋅ d = mvr cos α = mvτ r , где r расстояние от оси вращения до рассматриваемой материальной точки, vτ - составляющая
скорости, перпендикулярная радиус-вектору рассматриваемого точечного тела (рис. 76).
3
Однородность означает равноправие, одинаковость, всех точек пространства.
66
Аналогично моменту силы момент импульса может быть определен как векторная физическая
r
величина, направленная перпендикулярно плоскости, содержащей вектор импульса mv и радиус-вектор
r
r . При таком определении вектор момента импульса равен векторному произведению указанных векторов
r r
r
L = r × mv . Основное уравнение динами вращательного движения также записывается в векторной форме
r
r
∆L
=M.
(3)
∆t
Легко показать, что при вращении тела вокруг неподвижной оси, из формулы (3)
следует выражение для момента импульса L = Iω . Действительно, при вращении вокруг
неподвижной оси вектор скорости перпендикулярен прямой, соединяющей точку тела с
осью вращения, величина скорости выражается через угловую
скорость v = ωr (рис. 77). Поэтому момент импульса выражается
формулой L = mvr = mr 2ω = Iω , где I = mr 2 . Если же
рассмотреть вращение произвольного тела, то для того, чтобы
вычислить момент импульса всего тела, достаточно мысленно
разбить его на малые части и просуммировать моменты
импульсов всех малых частей. Так как угловые скорости всех
точек одинаковы, то суммирование сведется к суммированию
моментов инерции точек.
Легко заметить, что при движении произвольной системы материальных точек
изменение суммарного момента импульса полностью определяется моментом внешних
сил. По третьему закону Ньютона тела взаимодействуют с силами равными по величине и
противоположными по направлению. Так как силы взаимодействия направлены вдоль
одной прямой, то плечи этих сил равны. Следовательно, при суммировании уравнений
вращательного движения для произвольной системы моменты внутренних сил взаимно
уничтожатся (подобно тому, как взаимно уничтожаются внутренние силы при сложении
уравнений поступательного движения). Таким образом, для произвольной системы
r
материальных точек оказывается справедливым уравнение (3), в котором M - вектор
моментов только внешних сил.
Для замкнутой системы тел, не взаимодействующих с другими телами, не
включенными в систему, момент внешних сил равен нулю, поэтому для замкнутой
системы суммарный момент импульса сохраняется. Это утверждение выражает еще
один фундаментальный физический закон – закон сохранения момента импульса.
В теоретической физике показано, что он является следствием изотропности4
пространства, в котором происходят все физические явления. Если вы уверены в том, что
результаты физического эксперимента одинаковы, независимо от того, как ориентирована
ваша экспериментальная установка, то вы должны признать закон сохранения импульса.
6.3 Работа. Кинетическая энергия.
Продолжим наш разговор о результате действия силы. Во-первых, сила есть
причина ускорения (то есть изменения скорости) тела, во-вторых, если сила действует на
систему в течение некоторого промежутка времени, то результатом этого действия
является изменение импульса системы. Сейчас мы рассмотрим результат действия силы
на некотором пространственном интервале пути.
Рассмотрим
простейшую
ситуацию,
когда
тело
(материальная точка) движется вдоль прямой под действием
постоянной силы F , направленной вдоль той же прямой (рис.
78). В этом случае ускорение тела остается rпостоянным и
r F
определяется вторым законом Ньютона a = . Пусть тело
m
Изотропность означает равноправие, одинаковость, всех направлений в пространстве.
67
сместилось на расстояние ∆x , которое может быть выражено по кинематической формуле
v 2 − v02
. Объединяя эти две приведенные формулы, получим следующее выражение
∆x =
2a
mv 2 mv02
F∆x =
−
.
(1)
2
2
Итак, мы видим, что произведение силы на интервал времени ее действия равно
изменению импульса тела, то произведение силы на смещение тела равно изменению
mv 2
такой характеристики движения5 как K =
, которая, как вы знаете, называется
2
кинетической энергией тела.
Обсудим теперь общую ситуацию – тело движется по
произвольной траектории, результирующая внешняя сила не
является постоянной, может изменяться как по величине, так и по
направлению. Обозначим перемещение тела за малый промежуток
r
времени ∆r (рис. 79). Действующую силу (и ускорение) имеет
смысл разложить на две составляющих: тангенциальную F cos α ,
параллельную
вектору
перемещения,
и
нормальную,
перпендикулярную вектору перемещения F sin α . Как ранее было показано, нормальное
ускорение (и его причина сила) не изменяют модуля скорости (изменяется только ее
направление). Таким образом, изменение модуля скорости полностью определяется
тангенциальной составляющей силы. На малом интервале времени траекторию движения
можно приближенно считать отрезком прямой линии, поэтому для него применима
формула (1). Поэтому, изменение кинетической энергии тела на малом интервале
траектории равно произведению тангенциальной составляющей силы на модуль
перемещения
⎛ mv 2 ⎞
⎟⎟ = F cos α ⋅ ∆r .
∆⎜⎜
⎝ 2 ⎠
Правую часть этого выражения можно компактно записать в виде скалярного
r r
произведения векторов силы и перемещения F cos α ⋅ ∆r = F ⋅ ∆r . Эта физическая
величина играет чрезвычайно важную роль в физике, поэтому не случайно она получила
r r
«персональное» название – «механическая работа» - A = F ⋅ ∆r . Также не случайно, что
имеются специальные единицы измерения работы (и энергии): так в системе СИ единицей
измерения работы является Джоуль – работа, которую совершает сила в 1 ньютон при
Работа есть
перемещении тела на 1 метр в направлении действия силы.
характеристика действия силы: если под действием силы произошло перемещение тела, то
говорят, что сила совершила работу6. В результате совершенной работы происходит
изменение кинетической энергии тела.
Результат,
полученный
для
малого
перемещения, можно распространить на любой
участок траектории. Для этого достаточно разбить
траекторию на малые участки (рис. 80) и
просуммировать как произведенную работу, так и
5
В течение более сотни лет среди ученых-физиков шла бурная дискуссия, что является «мерой движения»:
r
импульс mv , или кинетическая энергия
6
mv 2
, которую называли «живой силой».
2
Мы знаем, что сила есть характеристика взаимодействия тел, поэтому можно говорить о работе,
совершенной одним телом над другим. Выражения «сила совершила работу», «тело совершило работу»
можно рассматривать как эквивалентные. Также аналогичными являются выражения «внешняя сила
совершила работу» и «над телом совершена работа».
68
изменение кинетической энергии.
2
r r r r r r
⎛ mv12 mv02 ⎞ ⎛ mv22 mv12 ⎞ ⎛ mv32 mv22 ⎞
mvкон
mv02
⎟
⎜
⎟
⎜
⎟
⎜
.
F1 ⋅ ∆r1 + F2 ⋅ ∆r2 + F3 ⋅ ∆r3 + ... = ⎜
+ ... =
−
+
−
+
−
−
2 ⎟⎠ ⎜⎝ 2
2 ⎟⎠ ⎜⎝ 2
2 ⎟⎠
2
2
⎝ 2
Таким образом, мы доказали теорему о кинетической энергии тела: изменение
кинетической энергии тела равно работе внешних сил.
В простейшем случае движения тела вдоль прямой и при постоянной силе работа
r r
равна произведению вектора силы на вектор перемещения A = F ⋅ S = FS cos α , где α угол между указанными векторами. Как следует из определения, работа может быть как
положительной, если угол α острый (в этом случае кинетическая энергия тела
возрастает), так и отрицательной, если угол α - тупой (в этом случае кинетическая
энергия уменьшается). Если сила не является постоянной, вычисление работы этой силы
требует особых приемов.
Пусть на тело, движущееся вдоль оси X , действует
внешняя сила, модуль которой зависит от координаты тела.
Построим график (рис. 81) зависимости модуля этой силы
от координаты F ( x) . При смещении тела на малую
величину ∆x можно пренебречь изменением величины силы
на этом малом интервале. Тогда работа, совершенная на
этом участке, может быть вычислена по формуле
δA = F ( x )∆x . Легко заметить, что численно она равна
площади «полоски», основанием которой является ∆x , а
высотой F ( x ) . Для произвольного интервала изменения координаты тела от x1 до x 2 ,
суммарная работа, совершенная переменной силой, будет численно равна площади
криволинейной трапеции под графиком функции F ( x ) .
Обсудим теперь результат действия внешних сил не на отдельное взятое тело
(материальную точку), а на систему взаимодействующих тел. В этом случае результат
действия внешних сил может проявляться не только в изменении кинетической энергии
системы, но и приводить к другим последствиям: изменению взаимного расположения тел
системы (например, деформации тела), изменению температуры системы, появлению
звука, света, электрических зарядов и так далее. Иными словами, результат воздействия
внешних сил зависит от внутренних свойств рассматриваемой системы, в частности от
характера внутренних сил системы. Однако оказывается возможным установить
чрезвычайно общие закономерности поведения систем, введя для них специальную
характеристику – энергию, частным случаем которой является кинетическая энергия.
Дать общее определение энергии системы чрезвычайно затруднительно (да и вряд ли возможно) –
эта физическая величина фигурирует во всех разделах физики, принимает множество различных форм, с
которыми вы будете знакомиться на протяжении всего изучения физики. Общим для всех этих форм
является то, что различные формы энергии могут переходить друг в друга в ходе многообразных
физических процессов, при этом оставаясь постоянной для замкнутых систем. Своеобразным образом
энергия является некоторой универсальной мерой различных форм движения7, а сохранение энергии
свидетельствует о неуничтожимости движения.
В механике под энергией понимают способность системы совершить
механическую работу. Если рассматриваемая система совершает положительную работу
над внешними телами, то энергия системы уменьшается на величину совершенной
работы; если внешние силы совершают положительную работу над системой, то энергия
системы возрастает на величину совершенной работы. Таким образом, энергия и работа
являются близкими взаимосвязанными, но не идентичными понятиями.
Так
работа
является характеристикой физических процессов, а энергия - характеристика
состояния системы, причем работа играет роль меры изменения энергии системы.
7
В данном случае мы имеем в виду не только механическое движение, а движение в философском смысле –
«всякое изменение вообще».
69
При изучении различных видов энергии мы будем рассматривать два подхода:
первый, внешние силы совершают работу над системой, второй – система совершает
работу над внешними телами. В обоих случаях изменение энергии равно совершенной
работе, что позволяет получать математические выражения для различных форм энергии.
Подойдем с этой точки зрения к понятию кинетической энергии. Мы показали, что
работа внешних сил, совершенная над телом, приводит к увеличению его кинетической
энергии, которая выражается формулой
mV 2
K=
.
(2)
2
Сейчас, покажем, что движущееся тело, способно совершить работу, которая в
точности определяется формулой (2).
Итак, пусть тело массой m , движется со скоростью V0 . Для торможения тела до
r
полной остановки к нему необходимо приложить некоторую силу F , направленную в
сторону, противоположную его скорости.
Для определенности будем считать, что
рассматриваемое тело взаимодействует с другим телом
M , причем природа сил взаимодействия может быть
любой (рис. 82). По третьему закону Ньютона,
движущееся тело действует на тормозящее тело с
r
силой F ' , равной по величине и противоположной по
r
направлению силе F . Следовательно, тело m посредством этой силы будет совершать
работу над телом M . Считая для простоты, что силы взаимодействия постоянны по
величине, можем записать, что смещение S движущегося тела до остановки определяется
кинематической формулой (т.к. конечная скорость равна нулю)
V2
S= 0 ,
2a
F
- модуль ускорения движущегося тела. С учетом этих соотношений, работа,
где a =
m
r
совершенная силой F ' (движущимся телом), рассчитывается следующим образом:
V02 mV02
=
,
A = F'S = F
2a
2
что в точности равно начальной кинетической энергии тела.
6.4 Потенциальная энергия.
Если тела взаимодействуют между собой, то есть если между ними действуют
силы, то в процессе их взаимного движения также может совершаться механическая
работа. Следовательно, можно говорить, что взаимодействующие тела обладают
энергией. Энергия, обусловленная взаимодействием тел, их взаимным расположением,
называется потенциальной. Если сила взаимодействия совершает положительную
работу, то потенциальная энергия этого взаимодействия уменьшается на величину
совершенной работы.
Как мы покажем в дальнейшем, многие взаимодействия обладают важнейшим
свойством: работа этих сил не зависит от формы траектории движения, а полностью
определяется начальным и конечным положением тела. Силы, которые
удовлетворяют
этому
условию,
называются
потенциальными,
или
8
консервативными .
При изучении энергетических характеристик различных
взаимодействий вопрос о зависимости (или независимости) работы о форме траектории
8
Термин «консервативные, используется в том смысле, что для систем, в которых действуют подобные
силы, справедлив закон сохранения механической энергии, о котором мы будем говорить позднее.
70
является важнейшим, поэтому при изучении взаимодействий мы всегда будем его
анализировать. Если взаимодействия удовлетворяет условию потенциальности, то можно
ввести специальную функцию от координат всех взаимодействующих тел, описывающую
взаимодействие – потенциальную энергию U . Строго говоря, эта функция от взаимного
расположения всех взаимодействующих тел. Однако во многих случаях можно
рассматривать движение одного тела, при условии, что остальные тела неподвижны, тогда
можно говорить о потенциальной энергии отдельного тела и рассматривать
потенциальную энергию как функцию координат только этого движущегося тела
U ( x, y, z ) . Эта функция имеет следующий физический смысл: работа потенциальной
силы при перемещения тела из одной точки с координатами (x1 , y1 , z1 ) в другую, с
координатами (x 2 , y 2 , z 2 ) равна изменению потенциальной энергии, взятому с
противоположным знаком:
A = − ∆U = −(U ( x 2 , y 2 , z 2 ) − U ( x1 , y1 , z1 )) .
(1)
Изменение знака в данном определении достаточно логично: если сила совершила
положительную работу ( A > 0 ) , то ее энергия уменьшается (∆U < 0 ) .
Условие потенциальности взаимодействия может быть сформулировано в
эквивалентном виде: работа потенциальной силы по любой замкнутой траектории
равна нулю. Доказательство этого утверждения непосредственно следует из определения
потенциальной энергии.
Действительно, пусть некоторое тело переместилось по
некоторой замкнутой траектории (рис. 83). Тогда при движении
от точки 1 до точки 2, работа силы определяется формулой (7)
A12 = −(U 2 − U 1 ) , а придвижении в обратном направление по
любой другой траектории, работа будет равна A21 = −(U 1 − U 2 ) .
Суммарная же работа будет равна нулю.
Заметьте, что в том случае, когда работа силы зависит от траектории движения,
нельзя определить функцию потенциальной энергии, так работа зависит не только от
начального и конечного положения тела.
Мы можем установить связь между силой и потенциальной энергией
r
взаимодействия. Пусть под действием силы F тело сместилось на малое расстояние ∆x
вдоль оси X , при этом совершена работа A = Fx ∆x (где Fx - проекция силы на ось X ).
Уменьшение потенциальной энергии равно совершенной работе, поэтому
∆U = − A = − Fx ∆x .
(2)
Из этой формулы также следует выражение, позволяющее определить силу по известной
потенциальной энергии взаимодействия
∆U
Fx = −
.
(3)
∆x
Аналогичным образом определяются проекции силы на другие оси координат.
Обратим внимание на еще одно общее обстоятельство, общее для различных видов
потенциальной энергии. Как следует из определения, физический смысл имеет изменение
потенциальной энергии, так как только изменение энергии определяет экспериментально
измеряемые величины – работу и силу. Следовательно, если к функции потенциальной
энергии U ( x, y, z ) во всех точках добавить постоянное слагаемое, то эта добавка никак не
скажется на поведении системы. Поэтому часто говорят, что потенциальная энергия
определяется с точностью до произвольного слагаемого, или нулевой уровень
потенциальной энергии выбирается произвольно.
Теперь мы можем дать еще одно толкование потенциальной энергии.
Потенциальная энергия тела U ( x, y, z ) , находящегося в точке с координатами
(x, y, z ) равна работе, которую совершают силы взаимодействия при перемещении
71
тела из данной точки, в точку с координатами (x 0 , y 0 , z 0 ) , где потенциальная энергия
принимается равной нулю U ( x0 , y 0 , z 0 ) = 0 .
Таким образом, потенциальная энергия в некоторой точке определяется силами
взаимодействия не только в данной точке, но и на всем пути до точки с нулевой
потенциальной энергией.
С другой стороны, если над системой внешние силы совершают работу, то энергия
системы увеличивается, причем изменение энергии системы равно совершенной работе.
Однако работа внешних сил может пойти на увеличение любого вида энергии системы –
кинетической, потенциальной и других.
Итак, для расчета потенциальной энергии необходимо доказать, что работа силы не
зависит от траектории движения, а затем подсчитать эту работу, которая и будет равна
изменению потенциальной энергии.
6.5 Потенциальная энергия тел, находящихся в поле тяжести.
Пусть тело массой m падает с некоторой высоты, проходя при этом путь h . Так
r
сила тяжести mg , действующая на это тело, постоянно, то работа этой силы вычисляется
элементарно A = mgh .
Покажем, что эта работа не зависит от траектории,
по которой движется тело. Разобьем произвольную
траекторию движения тела на малые участки,
r
перемещения на которых обозначим ∆r (рис. 84). Тогда
работа силы тяжести на этом малом участке определяется
r r
по формуле δA = mg ⋅ ∆r = mg∆r cos α , где α - угол
между вертикалью и вектором перемещения. Как следует
из рисунка ∆r cos α = ∆h , где ∆h - изменение высоты
тела. Таким образом, работа полностью определяется
только изменением высоты тела, его вертикальной
координаты, а не траектории движения. Для вычисления
работы силы тяжести на произвольном участке
необходимо просуммировать выражения для работ на малых участках, что сведется к
суммированию изменения высот. Следовательно, эта работа не зависит от формы
траектории, поэтому сила тяжести является потенциальной. Используя определение
потенциальной энергии, можно записать
∆U = mg (h1 − h2 ) ,
(1)
где h1 , h2 - начальная и конечная высоты, на которых находилось тело. Так как
потенциальная энергия определяется с точностью до постоянного слагаемого, то уровень,
от которого отсчитываются высоты, может быть выбран произвольно, поэтому выражение
для потенциальной энергии традиционно записывают в виде U = mgh . Важно отметить,
что положительным направлением вертикальной оси (в наших обозначениях это h )
считается направление вертикально вверх, в сторону противоположную силе тяжести.
Если тело движется вниз, то сила тяжести совершает положительную работу, поэтому
потенциальная энергия тела уменьшается.
Для увеличения потенциальной энергии, к телу необходимо
приложить внешнюю силу, которая совершит работу. Так, чтобы поднять
тело на некоторую высоту h к нему необходимо приложить внешнюю силу
r
r
F , превышающую силу тяжести mg (рис.85). Если поднимать тело
равномерно, то внешняя сила по модулю будет равна mg . В этом случае,
работа внешней силы будет минимальна и вычисляется элементарно
A = mgh . Эта работа внешней силы пошла на увеличение энергии тела, а
точнее потенциальной энергии его взаимодействия с Землей.
72
Если приложенная сила превышает силу тяжести, то в ходе подъема тела будет
возрастать его скорость, а, следовательно, и кинетическая энергия. В этом случае работа
внешней силы пойдет на увеличение как потенциальной, так и кинетической энергии тела.
В обоих рассмотренных случаях совершенная работа выступает в роли меры изменения
энергии, а еще точнее – меры перехода энергии из одной формы в другую.
6.6 Потенциальная энергия деформированной пружины.
Деформированная (например, растянутая) пружина
способна совершить работу. Действительно, если к
растянутой пружине прикрепить некоторое тело, то пружина
будет действовать на него с некоторой силой, под действием
которой тело начнем смещаться, следовательно, будет
совершена работа (рис. 86).
Сила, с которой пружина действует на тело, не
является постоянной, поэтому для вычисления работы
воспользуемся графическим методом. Построим график
зависимости силы упругости F = kx от координаты, который
является прямой линией (рис. 87). Площадь выделенного
треугольника под графиком равна максимальной работе,
которую может совершить пружина, понятно, что она равна
kx 2
1
A = kx ⋅ x =
.
(1)
2
2
Для того чтобы пружине приписать потенциальную
энергию, равную максимальной работе (1) необходимо
показать, что эта работа не зависит от траектории движения
тела. Чтобы доказать это утверждение, достаточно
r
рассмотреть работу на малом участке перемещения ∆r при
движении по произвольной траектории (рис. 88). В данном
r r
δA = F ⋅ ∆r = kx ⋅ ∆r cos α = kx ⋅ ∆x ,
случае
эта
работа
полностью определяется изменением деформации пружины
x , поэтому она не зависит от траектории движения тела.
Таким образом, силы упругости, подчиняющиеся
закону Гука, являются потенциальными, и потенциальная энергия деформированной
пружины определяется формулой
kx 2
U=
.
(2)
2
Нулевой уровень потенциальной энергии, рассчитываемой по формуле (2),
соответствует недеформированной пружине.
Подсчитаем, какую минимальную работу следует совершить, чтобы пружину,
жесткостью k , растянуть на величину x (рис. 89). Чтобы
деформировать пружину, к ней необходимо приложить
внешнюю силу.
Очевидно, что эта работа будет
минимальная в том случае, когда внешняя приложенная сила
в любой точке равна силе упругости, действующей со
стороны пружины, поэтому работа этой силы будет равна
kx 2
A=
, то есть увеличению потенциальной энергии пружины.
2
73
6.7 Потенциальная энергия гравитационного притяжения.
Все тела обладающие массой притягиваются друг к другу, с силой, подчиняющейся
закону всемирного тяготения И.Ньютона. Следовательно, притягивающиеся тела
обладают энергией взаимодействия.
Покажем, что работа гравитационных сил не зависит
от формы траектории, то есть гравитационные силы также
являются потенциальными. Для этого рассмотрим движение
небольшого тела массой m , взаимодействующего с другим
массивным телом массы M , которое будем полагать
неподвижным9 (рис. 90). Как следует из закона Ньютона сила
r
F , действующая между телами, направлена вдоль линии,
соединяющей эти тела. Поэтому при движении тела m по дуге
окружности с центром в точке, где находится тело M , работа
гравитационной силы равна нулю, так как векторы сил и
перемещения
все
время
остаются
взаимно
перпендикулярными. При движении вдоль отрезка,
направленного к центру тела M , векторы перемещения и
силы параллельны, поэтому в этом случае при сближении тел
работа гравитационной силы положительна, а при удалении
тел – отрицательна. Далее заметим, что при радиальном
движении работа силы притяжения зависит только от
начального и конечного расстояния между телами. Так при
движении по отрезкам (см. рис.91) DE и D1 E1 совершенные
работы равны, так законы изменения сил от расстояния на
обоих отрезках одинаковы. Наконец, произвольную траекторию тела m можно разбить на
набор дуговых и радиальных участков (например, ломаная ABCDE ). При движении по
дугам работа равна нулю, при движении по радиальным отрезкам работа не зависит от
положения этого отрезка – следовательно, работа гравитационной силы зависит только от
начального и конечного расстояния между телами, что и требовалось доказать.
Заметьте, что при доказательстве потенциальности мы воспользовались только тем фактом, что
гравитационные силы являются центральными, то есть направленными вдоль прямой, соединяющей тела, и
не упоминали о конкретном виде зависимости силы от расстояния. Следовательно, все центральные силы
являются потенциальными.
Мы доказали потенциальность силы гравитационного взаимодействия между двумя
точечными телами. Но для гравитационных взаимодействий справедлив принцип
суперпозиции – сила, действующая на тело со стороны системы точечных тел, равна
сумме сил парных взаимодействий, каждая из которых является потенциальной,
следовательно, и их сумма также потенциальна. Действительно, если работа каждой силы
парного взаимодействия не зависит от траектории, то и их сумма также не зависит от
формы траектории. Таким образом, все гравитационные силы потенциальны.
Нам осталось получить конкретное выражение для потенциальной энергии
гравитационного взаимодействия.
Для вычисления работы силы притяжения между
двумя точечными телами достаточно подсчитать эту работу
при движении вдоль радиального отрезка при изменении
расстояния от r1 до r2 (рис. 92).
9
Вспомните, что сила гравитационного взаимодействия между сферически симметричными телами
эквивалентна силе взаимодействия между точечными телами, таких же масс.
74
Очередной раз воспользуемся графическим методом, для чего построим
Mm
зависимость силы притяжения F = G 2
от
r
расстояния r между телами, тогда площадь под
графиком этой зависимости в указанных пределах
и будет равна искомой работе (рис. 93).
Вычисление этой площади представляет собой не
слишком сложную задачу, требующее, однако,
определенных математических знаний и навыков.
Не вдаваясь в детали этого расчета, приведем
конечный результат, для данной зависимости
силы от расстояния площадь под графиком, или
работа силы притяжения определяется формулой
⎛ 1 1⎞
A12 = GMm⎜⎜ − ⎟⎟ .
⎝ r2 r1 ⎠
Так как мы доказали, что гравитационные силы
являются потенциальными, эту работу равна уменьшению потенциальной энергии
взаимодействия, то есть
⎛ 1 1⎞
A12 = GMm⎜⎜ − ⎟⎟ = − ∆U = −(U 2 − U 1 ) .
⎝ r2 r1 ⎠
Из этого выражения можно определить выражение для потенциальной энергии
гравитационного взаимодействия
Mm
U (r ) = −G
.
(1)
r
При таком определении потенциальная энергия отрицательна и стремится к нулю
при бесконечном расстоянии между телами U (∞ ) = 0 . Формула (1) определяет работу,
которую совершит сила гравитационного притяжения при увеличении расстояния от r до
бесконечности, так как при таком движении векторы силы и перемещения направлены в
противоположные стороны, то эта работа отрицательна. При противоположном движении,
при сближении тел от бесконечного расстояния до расстояния r , работа силы притяжения
будет положительна. Эту работу можно подсчитать по определению потенциальной
Mm
.
энергии A∞ → r = −(U (∞ ) − U (r )) = G
r
Подчеркнем,
что
потенциальная
энергия
является
характеристикой
взаимодействия, по меньшей мере, двух тел. Нельзя говорить о том, что энергия
взаимодействия «принадлежит» одному из тел, или каким образом «разделить эту
энергию между телами». Поэтому, когда мы говорим об изменении потенциальной
энергии, мы подразумеваем изменение энергии системы взаимодействующих тел. Однако
в некоторых случаях допустимо все же говорить об изменении потенциальной энергии
одного тела. Так, при описании движения небольшого, по сравнению с Землей, тела в поле
тяжести Земли, говорим о силе действующей на тело со стороны Земли, как правило, не
упоминая и не учитывая равную силу, действующую со стороны тела на Землю. Дело в
том, что при громадной массе Земли, изменение ее скорости исчезающее мало. Поэтому
изменение потенциальной энергии взаимодействия приводит к заметному изменению
кинетической энергии тела и бесконечно малому изменению кинетической энергии Земли.
В такой ситуации допустимо говорить о потенциальной энергии тела вблизи поверхности
Земли, то есть всю энергию гравитационного взаимодействия «приписать» небольшому
телу. В общем случае можно говорить о потенциальной энергии отдельного тела, если
остальные взаимодействующие тела неподвижны.
75
Мы неоднократно подчеркивали, что точка, в которой потенциальная энергия принимается равной
нулю, выбирается произвольно. В данном случае такой точкой оказалась бесконечно удаленная точка. В
некотором смысле этот непривычный вывод, может быть признан разумным: действительно, на
бесконечном расстоянии исчезает взаимодействие – исчезает и потенциальная энергия. С этой точки зрения
логичным выглядит и знак потенциальной энергии. Действительно, чтобы разнести два притягивающиеся
тела внешние силы должны совершить положительную работу, поэтому в таком процессе потенциальная
энергия системы должна возрастать: вот она возрастает, возрастает и … становится равной нулю!
Если притягивающиеся тела соприкасаются, то сила притяжения не может совершать положительную
работу, если же тела разнесены, то такая работа может быть совершена при сближении тел. Поэтому часто
говорят, о том, что притягивающиеся тела обладают отрицательной энергией, а энергия
отталкивающихся тел положительна. Это утверждение справедливо, только в том случае, если нулевой
уровень потенциальной энергии выбирается на бесконечности.
Так если два тела связаны пружиной, то при увеличении расстояния между телами, между ними
будет действовать сила притяжения, тем не менее, энергия их взаимодействия является положительной. Не
забывайте, что нулевому уровню потенциальной энергии соответствует состояние недеформированной
пружины (а не бесконечность).
6.8 Работа сил трения.
При относительном движении одного тела по поверхности другого возникают силы
трения, то есть тела взаимодействуют друг с другом. Однако этот вид взаимодействия
принципиально отличается от рассмотренных ранее. Наиболее существенным отличием
является тот факт, что сила взаимодействия определяется не взаимным расположением
тел, а их относительной скоростью. Следовательно, работа этих сил зависит не только от
начального и конечного положения тел, но и от формы траектории, от скорости
перемещения. Иными словами, силы трения не являются потенциальными.
Рассмотрим подробнее работу различных видов трения.
Самой простой случай – трения покоя. Достаточно сказать, что при отсутствии
перемещения, работа равна нулю, поэтому трения покоя работы не совершает.
При движении одного тела по поверхности другого возникает сила сухого трения.
По закону Кулона-Амонтона величина силы трения постоянна и направлена в сторону
противоположную скорости движения. Следовательно, в любой момент времени, в любой
точке траектории векторы скорости и силы трения направлены в противоположные
стороны, угол между ними равен 180° (вспомните cos 180° = −1 ). Таким образом, работа
силы трения равна произведению силы трения на длину траектории S :
Aтр. = − Fтр. S .
(1)
Между двумя точками можно проложить сколько угодно траекторий, длины
которых могут изменяться в широких пределах, при движении по каждой из этих
траекторий сила трения будет совершать различную работу.
Использование понятия работы оказывается полезным и при наличии сил трения.
Рассмотрим простой пример. Пусть на горизонтальной поверхности находится брусок,
которому толчком сообщили скорость v 0 . Найдем, какой путь пройдет брусок до
остановки при наличии сухого трения, коэффициент которого равен µ . Так как при
остановке кинетическая энергия обращается в нуль, то изменение кинетической энергии
mv 2
mv 2
тела равно ∆E кин. = 0 − 0 = − 0 . По теореме о кинетической энергии, изменение
2
2
последней равно работе внешних сил. Единственной силой, совершающей работу,
является сила трения, которая равна в данном случае Aтр. = − µmgS . Приравнивая эти
v02
.
выражения, легко находим путь до остановки S =
2 µg
Для того, чтобы рассматриваемый брусок двигался по горизонтальной поверхности
с постоянной скоростью к нему необходимо прикладывать постоянную горизонтально
направленную силу F , равную по модулю силе трения. Эта внешняя сила будет
совершать положительную работу A , равную по модулю работе силе трения.
76
Кинетическая энергия бруска при таком движении возрастать не будет. Заметим, что
противоречия с теоремой о кинетической энергии в этом утверждении нет – так
суммарная внешняя сила, действующая на брусок, равна нулю. Тем не менее, необходимо
твердо уяснить, что работа всякой силы есть мера перехода энергии из одной формы в
другую, поэтому следует определить, какие изменения с системой (бруском и
поверхностью) произошли в результате совершенной работы.
Ответ известен –
произошло нагревание, как поверхности, так и бруска. Иными словами работа внешней
силы пошла на увеличение внутренней, тепловой энергии. Аналогично, при торможении
начальная кинетическая энергия бруска перешла во внутреннюю энергию. В любом
случае работа силы трения приводит к увеличению тепловой энергии.
При движении тела в вязкой среде, на тело действует сила сопротивления,
зависящая от скорости и направленная в сторону противоположную вектору скорости,
поэтому работа этих сил всегда отрицательна, причем зависит от траектории движения
тела. Следовательно, силы вязкого трения не являются потенциальными.
Преобразования энергии, происходящие при наличии вязкого трения аналогичны
рассмотренным ранее, правда их расчет усложняется зависимостью сил от скорости. Не
потенциальные силы, приводящие к увеличению внутренней энергии, называются
диссипативными10. Примерами таких сил являются силы трения.
6.9 Закон сохранения энергии.
Пусть некоторое материальное тело взаимодействует с другими неподвижными
телами, причем все силы взаимодействия являются потенциальными. Обозначим
кинетическую энергию тела в некоторый начальный момент времени K 0 , а
потенциальную энергию его взаимодействия с другими телами в тот же момент времени
U 0 , через K ,U - обозначим кинетическую и потенциальную энергии в произвольный
момент времени. В этом случае изменение кинетической энергии тела ∆K = K − K 0 = A ,
согласно доказанной нами теореме, равно работе внешних сил. С другой стороны, по
определению потенциальной энергии, работа потенциальных сил равна изменению
потенциальной энергии, взятой с противоположным знаком A = − ∆U = −(U − U 0 ) .
Приравнивая эти выражения, получим уравнение
K − K 0 = −(U − U 0 ) ,
которое перепишем в виде
K + U = K0 + U0 .
(1)
Сумма кинетической и потенциальной энергия тела называется механической энергией.
Полученное уравнение (15) указывает, что при сформулированных условиях сумма
кинетической и потенциальной энергий тела (его механическая энергия) остается
постоянной в процессе движения.
Рассмотрим теперь движение двух
взаимодействующих тел. Будем считать для
упрощения, что два небольших тела движутся
навстречу друг другу вдоль одной прямой,
соединяющей эти тела (рис. 94). Применим
теорему о кинетической энергии для каждого
тела для их малых смещений ∆r1 , ∆r2 за малый промежуток времени
∆K 1 = F12 ∆r1
.
(2)
∆K 2 = F21 ∆r2
Просуммируем эти уравнения с учетом равенства модулей сил, действующих на каждое
тело ( F12 = F21 = F ) .
10
Термин «диссипативные» означает «рассеивающие» - эти силы «рассеивают механическую энергию».
77
∆(K 1 + K 2 ) = F (∆r1 + ∆r2 ) .
Теперь обратим внимание, что сумма смещений тел есть изменение расстояния между
телами. Так как, сила взаимодействия зависит только от расстояния между телами, то
выражение F (∆r1 + ∆r2 ) = −(U − U 0 ) совпадает с выражением для работы силы
взаимодействия при условии, что одно из тел покоится, следовательно, оно равно
изменению потенциальной энергии взаимодействия, взятой с противоположным знаком
∆K = −∆U , или K + U = const .
Таким образом, мы получаем, что увеличение суммарной кинетической энергии равно
уменьшению потенциальной энергии взаимодействия, поэтому суммарная механическая
энергия системы из двух тел сохраняется. Этот вывод достаточно легко можно обобщить
на произвольную замкнутую систему тел, все силы взаимодействия между которыми
потенциальны. Отметим, что системы, в которых отсутствуют диссипативные силы,
называются консервативными.
Итак, механическая энергия замкнутой консервативной системы сохраняется.
Это чрезвычайно важное утверждение составляет содержание закона сохранения
механической энергии. Подчеркнем, для сохранения механической энергии необходимо
выполнение двух условий: первое, система должна быть замкнута, то есть не
взаимодействовать с другими телами; второе, система должна быть консервативна, то есть
все силы взаимодействия должны быть потенциальными.
Рассмотрим теперь систему, в которой присутствуют неконсервативные
(диссипативные) силы. Опять для упрощения алгебраических выкладок, будем считать,
что система состоит из двух описанных
ранее тел, на каждое из которых помимо сил
взаимодействия, действуют диссипативные
r r
силы Fд1 , Fд 2 , которые не обязаны быть
одинаковыми,
являясь
абсолютно
независимыми (рис. 95). В этом случае в
каждом уравнении системы (2) появится дополнительное слагаемое, описывающее работу
диссипативных сил
r r
∆K 1 = F12 ∆r1 + Fд1 ∆r1
(3)
r r.
∆K 2 = F21 ∆r2 + Fд 2 ∆r2
Проводя над этой системой аналогичные преобразования, получим уравнение
∆(K + U ) = Aд ,
(4)
r r r r
где Aд = Fд1 ∆r1 + Fд 2 ∆r - суммарная работа диссипативных сил в системе (заметим, что,
как правило, эта работа отрицательна). Эти рассуждения легко обобщаются на систему
произвольного числа тел.
Таким образом, в замкнутой неконсервативной системе изменение
механической энергии равно работе диссипативных сил.
Наконец, можно рассмотреть не замкнутую систему, то есть ситуацию, когда на
тела системы действуют внешние силы любой природы. В этом случае в уравнения типа
(2) следует включить работу внешних сил, после аналогичных преобразований можно
прийти к выводу: в незамкнутой неконсервативной системе изменение полной
механической энергии равно сумме работы внешних сил и работы диссипативных
сил.
Второй способ описания таких систем заключается в их расширении: достаточно в
нее включить все взаимодействующие тела и рассматривать расширенную систему как
замкнутую.
Мы уже отмечали, что всякая работа есть мера перехода энергии из одной формы в
другую. Так в рассмотренных случаях работа потенциальных сил приводит к изменению
кинетической энергии, эта работа показывает, сколько энергии перешло из кинетической
78
в потенциальную (или обратно). Наличие сил трения приводит к выделению теплоты,
работа этих сил показывает, сколько механической энергии перешло во внутреннюю,
тепловую. Если в энергию системы включить и ее внутреннюю энергию, то можно
сделанный вывод можно переформулировать в виде закона сохранения энергии: в
замкнутой системе полная энергия сохраняется.
Этот закон является предельно общим – он справедлив для любых физических явлений. В ходе
дальнейшего изучения физики мы постоянно будем обобщать этот закон, включая в него иные формы
энергии – электрическую, магнитную, атомную, ядерную и т.д. Смело можно утверждать, что закон
сохранения энергии является основой современной физики. В любых явлениях мы будем искать и находить
формулы для различных форм энергии. Что общего в этих различных формах энергии – энергия может
переходить, превращаться из одной формы в другую, поэтому справедливо уважительно расширить
название закона – ЗАКОН СОХРАНЕНИЯ И ПРЕВРАЩЕНИЯ ЭНЕРГИИ.
Невозможно назвать одного автора этого закона, многие физики внесли свой вклад в его
формулировку, обоснование и развитие - от неизвестных авторов, сформулировавших «золотое правило
механики» до современных исследователей. С некоторыми из них мы познакомимся в дальнейшем.
Что касается его проявления в механических явления, то полученные нами уравнения следуют из
уравнений законов Ньютона и свойств конкретных взаимодействий. Но закон сохранения энергии имеет
более широкие и общие рамки, да и его обоснование имеет более прочный фундамент. Так как этот закон
тесно связан с однородностью времени – если вы уверены, что результаты физического эксперимента
проведенного сегодня, приведут завтра (при сохранении всех условий) к тем же результатам, вы должны
быть уверены в законе сохранения энергии.
6.10 Заметки о симметрии.
Хотя в физике очень много сложного, в ней также много простоты и изящества, что
в значительной мере обусловлено симметрией физических законов и систем. В
соответствии с этим симметрия не только занимает важное место в физике, но и играет
все возрастающую роль в современных физических исследованиях.
Симметрия в широком смысле – свойство геометрической фигуры,
характеризующее некоторую правильность формы, неизменность ее при движениях и
зеркальных отображениях.
Рассмотрим некоторые виды и элементы симметрии.
1. Симметрия относительно плоскости (зеркальная симметрия) .
Две точки A и A' симметричны относительно плоскости П , если они
расположены на одном перпендикуляре к плоскости и на равном расстоянии от нее (рис.
96). Фигуры и тела симметричны относительно плоскости, если для каждой точки тела,
существует симметричная относительно плоскости другая точка тела. Плоскостью
симметрии могут обладать как плоские, так и объемные фигуры. Тела могут обладать и
несколькими плоскостями симметрии, так фигура, показанная на рисунке, обладает
двумя плоскостями симметрии. Если ввести декартовую ось координат Z ,
перпендикулярную плоскости симметрии, то любая характеристика системы будет
сохраняться при изменении знака этой координаты F ( x, y, z ) = F ( x, y,− z ) .
79
2 . Оси симметрии.
Тело обладает осью симметрии n -го порядка On , если при вращении вокруг этой
оси, тело n раз совмещается с самим собой (рис. 97).
Если фигура совмещается сама с собой при повороте на любой угол, то такое тело
называется осесимметричным, а прямая, вокруг которой можно проводить поворот на
любой угол без изменения формы фигуры, называется осью симметрии. Формально ось
симметрии можно рассматривать как ось симметрии бесконечного порядка O∞ .
Простейшей пространственной фигурой, обладающей осью симметрии, является цилиндр,
поэтому такой тип симметрии также называют цилиндрической симметрией.
Заметим, что любая плоскость, содержащая ось симметрии, является плоскостью
симметрии.
Сферическая (центральная) симметрия. Тело обладает центром симметрии, если любая
прямая проходящая через центр, является осью симметрии. Иными словами, тело можно
повернуть на любой угол относительно любой прямой, проходящей через центр
симметрии. Такой симметрией обладает сфера (чем и обусловлено ее название).
Любая характеристика системы, обладающей сферической симметрией, зависит только от
расстояния до центра. Так сила гравитационного притяжения между точечными телами
зависит только от расстояния между телами, поэтому говорят, что эта сила сферически
симметрична.
80
Трансляционные симметрии. Этот вид симметрии
связан с восстановлением тел при их смещении.
Понятно, что такими видами симметрии обладают
только бесконечно большие тела. В некоторых
случаях
системы
повторяют
себя
строго
определенных смещениях. Так для бесконечной
плоскости, покрытой рисунками (рис. 98), при ее
r
r
r
смещении на векторы A = k x a x + k y a y (где k x , k y -
любые целые числа) происходит ее совмещение с
начальным положением. Такой вид симметрии
присущ кристаллам, поэтому его изучение играет
важную роль в кристаллографии.
Некоторые системы повторяют себя при
смещении на произвольное расстояние в
определенном направлении. Таким свойством
обладает, например, бесконечно длинный прямой
цилиндр произвольного сечения (рис. 99).
Для однородной плоскости, восстановление
происходит при смещении на любой расстояние вдоль любого вектора, параллельного
плоскости.
Наконец, в однородном веществе, можно провести сдвиг в любом направлении на
любое расстояние.
Симметрии реальных физических систем обладают свойством «самосохранения»,
так если источники (света, электрические заряды и т.д.) обладают какой либо симметрией,
то такой же симметрией обладают и результаты действия этих источников.
81
§7. Механика жидкости и газа.
Рассмотренные нами методы описания механического движения, законы,
управляющие этим движением, в принципе, позволяют изучать движение любой
механической системы. Основные проблемы, возникающие при этом, носят скорее
математический характер – может понадобиться слишком много переменных, слишком
много уравнений, слишком много расчетов. Поэтому до настоящего времени
продолжаются научные исследования в области механики – строятся новые модели,
разрабатываются новые (в том числе компьютерные) методы решения уравнений,
анализируются возможности применения различных упрощений и приближений.
В данном параграфе мы рассмотрим основы описания движения жидкостей и газов.
Данный раздел физики называется гидродинамика и аэродинамика. Даже основные
уравнения этого раздела чрезвычайно сложны, их формулировка и обоснование требует
привлечения не только законов механики, но и законов, описывающих процессы
теплопередачи, упругих свойств жидких и газообразных сред, и других. Поэтому мы
только наметим некоторые основные идеи, тем более что математический аппарат,
привлекаемый для описания вполне наглядного движения жидкости, понадобится нам при
изучении более абстрактных электрических и магнитных полей.
7.1 Модель сплошной среды, «точечные» характеристики вещества.
Хорошо известно, что все тела, в том числе жидкие газообразные, состоят из молекул.
Поэтому если задать положение каждой молекулы в произвольный момент времени, то
движение жидкости или газа будет описано очень подробно. Однако очевидно, что
выполнение этой программы невозможно1 – достаточно вспомнить, что в 1 см 3 содержится
более чем 1019 молекул. Чтобы только выписать нужное число уравнений движения не
хватит ни бумаги, ни чернил, ни времени. Более того, такое сверхподробное описание
является явно излишним, извлечь полезные сведения из такого массива информации
просто невозможно. Итак, нам необходим принципиально иной способ описания
движения жидкости.
Прежде всего, отметим, что в подавляющем большинстве случаев описания
движения жидкостей и газов нет необходимости рассматривать молекулярную структуру
– так как размеры движущихся объемов жидкости, размеры движущихся в жидкости
твердых тел значительно превышают размеры молекул. Поэтому в этих случаях
используется модель сплошной среды. В рамках этой модели газ или жидкость
рассматривается как среда, все характеристики которой плавно и непрерывно изменяются
от одной геометрической точки к другой. В рамках такой модели можно вводить
«точечные» характеристики среды (например, плотность, удельная теплоемкость,
вязкость, показатель преломления, удельное электрическое сопротивление) и
рассматривать их как функции координат точек среды. Если свойства среды одинаковы
во всех точках пространства, то такая среда называется однородной. С точки зрения
математики использование модели сплошной среды означает переход от дискретного к
непрерывному описанию. Рассмотрим для примера понятие плотности неоднородной
среды. Для однородного вещества плотность ρ равна отношению массы тела m к его
m
объему V , или массе единицы объема тела - ρ = . Для однородного вещества
V
отношение массы к объему является величиной постоянной.
1
Справедливости ради, отметим, что в настоящее время разрабатывается и используется, так называемый,
динамический подход к исследованию молекулярных систем, в рамках которого жидкость, газ моделируется
как набор небольших тел (материальных точек, жестких шариков, дисков) движущихся и
взаимодействующих по законам механики. В рамках этих исследований получены достаточно интересные
результаты. Однако, число частиц, входящих в моделируемую систему, мало - не превышает миллиона
6
( 10 ). Реализация таких моделей возможна только с помощью мощных современных компьютеров.
82
В качестве примеров неоднородных веществ можно привести смеси различных
веществ; земную атмосферу, плотность которой уменьшается с высотой, плохо
перемешенные растворы и т.д. Для тела, изготовленного из неоднородного вещества,
m
дает только среднее значение плотности тела.
введенное понятие плотности ρ =
V
Для более подробного описания распределения масс в таких телах, можно мысленно
разбить тело на малые части (рис. 100), указать номер i
«кусочка», определить его объем Vi и массу mi , рассчитать
mi
. Для увеличения точности
Vi
описания число частей должно увеличиваться, соответственно
будет возрастать и число средних плотностей. Фактически
набор величин ρ i представляет собой среднюю плотность как
функцию номера выделенной части. Понятно, что такое
описание не очень удобно.
Поэтому принят другой метод описания распределения масс внутри неоднородного
тела. Выберем внутри тела точку с координатами (x, y, z ) и вокруг нее очертим некоторый
объем ∆V (его форма – кубик, шарик … несущественна), определим массу вещества,
содержащегося внутри выделенного объема ∆m и среднюю плотность этого выделенного
∆m
объема ρ (x, y, z ) =
. Далее мысленно будем уменьшать объем выделенной части,
∆V
соответственно будет уменьшаться и масса этой части. Предел, к которому стремится
средняя плотность при уменьшении объема, и называется плотностью вещества в данной
точке
∆m
ρ ( x, y , z ) =
, при ∆V → 0 .
∆V
При таком определении плотность становится непрерывной функцией координат.
Аналогично определяются и другие «точечные» характеристики вещества.
С математической точки зрения для описания характеристик сплошной среды, мы
используем функции нескольких переменных – координат и времени (в принципе
характеристики среды могут изменяться с течением времени). Такое соответствие – когда
каждой точке пространства (трем координатам) ставится в соответствие число, в
математике называется скалярным полем. В этом математическом смысле говорят о поле
температур, поле давлений, поле плотностей и т.д.
среднюю плотность
ρi =
Обратите внимание, на формальную схожесть определения плотности «в точке» с определением
мгновенной скорости. Строго говоря, понятие плотности «в точке» физического смысла не имеет –
измерению поддается только средняя плотность конечного объема вещества. Особенно абсурдным
становится понятие плотности газа, в пределах объема, размеры которого меньше среднего расстояния
между молекулами!
Реальный смысл имеет произведение ρ ( x, y, z )∆V равное массе вещества в малом
объеме ∆V , окружающем точку с координатами (x, y, z ) . Тем не менее, упрощение
математического описания, искупает логическую противоречивость. В некоторых
случаях, говоря о бесконечно малом объеме, подразумевают физически бесконечно малый
объем – с точки зрения математического описания малый, а с
физической велик по сравнению со средним расстоянием между
молекулами, содержащий достаточно много молекул. В таком
объеме, свойства отдельных частиц (например, их массу) мы
равномерно «размазываем» по всему объему, сохраняя ее суммарное
значение (рис. 101).
83
16.2 Кинематическое описание движения жидкости и газа – «гидрокинематика».
Поле скоростей.
При кинематическом описании движения любой механической системы нет
необходимости подробно рассматривать внутренние физические свойства тел,
включенных в систему. При описании движения жидкости достаточно принять во
внимание ее текучесть – способность изменять свою форму при малейшем внешнем
воздействии. Свойства жидкостей и газов существенно различаются, однако описание
движения жидкостей и газов сходно, поэтому в данном разделе, говоря об описании
движения жидкости, будем иметь виду, что описание движения газов проводится
аналогично.
Если нас интересует движение жидкости целиком, а не конкретно какой-либо
молекулы, мы можем говорить о скорости жидкости в данной точке, в данный момент
времени. Иными словами, будем следить не за отдельной частицей жидкости (ее
скоростью, траекторией и другими характеристиками), а за скоростью жидкости в данной
пространственной точке, не обращая внимания, что в другой момент времени в
рассматриваемой точке будет находиться другая частица жидкости. Таким образом,
основной характеристикой движения будем считать пространственное распределение
r
скоростей жидкости, которое задается векторной функцией V (t , x, y, z ) - функцией,
задающей вектор скорости жидкости, в любой точке, в любой момент времени. Конечно,
математически такая конструкция очень сложна: вспомните, обычная функция f ( x )
каждому числу (аргументу x ) ставит в соответствие другое число (значение функции). В
нашем же случае четырем числам (трем координатам и времени) ставится в соответствие
три числа (компоненты вектора). В математике такое соответствие является обобщением
понятия функции и называется2 векторным полем. Поэтому введенная функция
r
V (t , x, y, z ) часто называется полем скоростей. В частом случае распределение скоростей
может сохраняться в течение некоторого промежутка времени, тогда функция
r
r
V (t , x, y, z ) = V ( x, y, z ) не зависит от времени, такое поле скоростей называется
стационарным. Если же скорости движения жидкости одинаковы во всех точках, то поле
скоростей называется однородным. Подчеркнем, стационарное – значит, в
рассматриваемом временном промежутке скорости остаются постоянными (но могут быть
различными в разных точках); однородное – значит, в рассматриваемом объеме скорости
одинаковы во всех пространственных точках (но могут изменяться с течением времени).
На первый взгляд, мы изменили сформулированную ранее основную задачу механики – определить
закон движения. Однако, в задачах движения жидкости, как правило, бывают важны другие характеристики:
расход жидкости, распределение давлений, силы сопротивления, подъемная сила крыла и т.д. Все эти и
многие другие характеристики могут быть рассчитаны, если известно распределение скоростей жидкости.
Фактически мы признаем, что сплошная среда обладает бесконечно большим числом степеней свободы. Так
одна материальная точка обладает тремя степенями свободы, при непрерывном описании каждая
геометрическая точка рассматривается в некотором смысле как материальная. В частности, мы определяем
вектор скорости (его три компоненты) в каждой точке, число которых, очевидно, бесконечно. При
r
дискретном описании мы должны задать скорости Vi (i = 1,2,3...) для каждой частицы (условно говоря,
вектор скорости, как функцию номера частицы), вместо этого мы определяем скорость как функцию трех
r
V ( x, y , z )
Наглядно представить себе векторное поле достаточно
затруднительно – в каждой точке необходимо изобразить вектор,
что конечно невозможно. Поэтому используются несколько
упрощенных способов графического представления векторных
полей. Наиболее часто встречается изображение векторных с
помощью линий поля – линии, касательные к которым
непрерывных координат
2
Подчеркнем, это тоже чисто математический термин, в дальнейшем мы будем рассматривать физические,
то есть реальные поля.
84
совпадают с вектором поля (рис. 102).
В рассматриваемом случае поля скоростей – линия поля называются линиями тока.
Линия тока – такая линия, касательная к которой в каждой точке совпадает с
направлением вектора скорости в данной точке. На линиях тока принято указывать
направление движения жидкости. Заметим, что линию тока можно провести через любую
точку, поэтому число линий, их густота определяются исключительно эстетическими
соображениями.
Семейство линий тока достаточно наглядно представляет движение жидкости в
некоторой области (рис. 103). Исходя из определения, можно установить их общие
свойства:
1. Линии тока не пересекаются (в противном случае, в
точке пересечения можно построить две касательных, то
есть в одной точке, скорость жидкости имеет два
значения, что абсурдно).
2. Линии тока не имеют изломов (в точке излома опять
можно построить две касательных).
3. Линии тока начинаются на источниках и
заканчиваются на точках стока жидкости.
Если движение жидкости является стационарным,
то линии тока совпадают с траекториями движения частиц жидкости. В нестационарном
потоке, линии тока изменяются с течением времени, поэтому траектория отдельно взятой
частицы отличается от линии тока. В этом случае линии тока следует рассматривать как
вспомогательные математические иллюстрации, не имеющие явного физического смысла.
Задания для самостоятельной работы.
1. Постройте семейство линий тока однородного поля скоростей.
2. Нарисуйте семейство линий тока, исходящих во все стороны от небольшого
источника.
7.3 Поток жидкости.
Пусть нам известно поле скоростей движущейся жидкости. Рассчитаем объем
жидкости, протекающей в единицу времени через некоторую воображаемую площадку,
часто эту характеристику называют расход, или поток жидкости Φ . Проще всего решить
данную задачу для однородного потока жидкости.
∆S
Пусть
воображаемая
площадка,
площадью
расположена перпендикулярно однородному потоку жидкости,
r
движущейся со скоростью V (рис. 104). За промежуток времени
∆t через площадку пройдет жидкость, находящаяся на
расстоянии меньшем, чем V∆t , объем этой жидкости будет равен
V∆t ⋅ ∆S . Итак, в единицу времени, через площадку пройдет
объем жидкости равный
∆Φ = V∆S .
(1)
Пусть площадка расположена под некоторым углом к
набегающему потоку жидкости, который, по-прежнему,
считаем однородным (рис. 105). Ориентацию площадки
удобно задавать, указывая вектор нормали к этой
r
площадке n - модуль, которого равен единице, а
направлен перпендикулярно площадке. Пусть вектор
r
скорости жидкости V образует угол α с вектором
r
нормали n к площадке, площадью ∆S . Объем жидкости,
протекающей через площадку за время ∆t , может быть
85
найден по формуле V∆t cos α ⋅ ∆S . Следовательно, расход (поток) жидкости через
площадку определяется выражениями
r r
∆Φ = V cos α∆S = V ⋅ n ∆S = Vn ∆S .
(2)
r r
r
r
где V ⋅ n = V cos α - скалярное произведение векторов V и n ; Vn - нормальная к
площадке компонента вектора скорости. Отметим, что согласно определению поток
может быть как положительным, так и отрицательным. Знак потока определяется
выбором направление нормали к поверхности, в конце концов, этот произвол, обусловлен
выбором
положительного
направления
движения
жидкости.
Наконец, в произвольном поле скоростей, объем
жидкости, протекающий в единицу времени через
произвольную поверхность, подсчитаем следующим
образом (рис. 106): разобьем поверхность на малые
площадки ∆S (которые будем считать плоскими),
r
определим вектор скорости жидкости V на этой
площадке (который в пределах площадки будем считать
постоянным), запишем выражение (2) для расхода
жидкости через площадку, просуммируем по всем
площадкам рассматриваемой поверхности.
Φ = ∆Φ 1 + ∆Φ 2 + ∆Φ 3 + ... =
∆Φ i =
Vi cos α i ⋅ ∆S i .
(3)
(
)
(
)
∑
i
∑
i
Эта сумма называется потоком вектора скорости через заданную поверхность.
Подобную сумму в некоторых случаях можно вычислить достаточно просто,
иногда ее вычисление может быть громоздким. Заметьте, что скорость жидкости мы
определяем в каждой точке (говорят, что это точечная характеристика), поток через
поверхность определяется движением жидкости в некоторой части пространства, поэтому
эта характеристика является интегральной, описывающей свойства движения обобщенно,
усреднено для этой части пространства.
Оказывается, что некоторые законы движения жидкости могут быть
сформулированы как теоремы для потока жидкости. С использованием таких теорем
можно решать многочисленные и сложные задачи.
Приведем примеры таких «очевидных» теорем.
«Первая теорема о потоке несжимаемой жидкости»: Если в некоторой области
движущейся несжимаемой жидкости отсутствуют источники и стоки, то поток
жидкости, через любую замкнутую поверхность равен нулю Φ = 0 .
Конечно, все реальные жидкости могут изменять свой объем, под действием
внешних сил. Однако изменение объема жидкостей обычно настолько мало, что им можно
пренебречь, именно такое приближение используется в модели несжимаемой жидкости.
Для
замкнутой
поверхности
положительной
принимается внешняя нормаль, направленная наружу от объема,
ограниченного рассматриваемой поверхностью (рис. 107). В
этом случае на одних частях поверхности поток будет
положительным (там, где жидкость вытекает из ограниченного
объема), на других отрицательным (там, где жидкость втекает
внутрь объема). Так как объем жидкости внутри поверхности
остается постоянным, то количество жидкости втекающей
внутрь равно количеству жидкости вытекающей наружу – вот
смысл сформулированной теоремы.
86
Применим эту теорему к жидкости, протекающей по трубе переменного сечения,
сочлененной из двух труб, площадь поперечного
сечения первой S1 , второй S 2 (рис. 108). В
качестве поверхности, к которой применим
теорему о потоке жидкости, выберем часть боковой
поверхности в месте сочленения и две плоских
площадки
перпендикулярных
оси
трубы,
находящиеся в широкой и узкой части. Скорость
жидкости в широкой части обозначим V1 , а в узкой
части V2 . Поток через боковую поверхность равен
нулю Φ бок = 0 , так как здесь векторы скорости и
нормали взаимно перпендикулярны, поток через площадку в широкой части трубы равен
Φ 1 = −V1 S1 (знак минус появился, так как векторы направлены в противоположные
стороны), поток через площадку в узкой части трубы Φ 2 = V2 S 2 . Таким образом, поток
через оговоренную поверхность равен
Φ = Φ 1 + Φ бок + Φ 2 = −V1 S1 + V2 S 2 = 0 .
Из этого соотношения получим уравнение, связывающее скорости в разных частях трубы
V1 S1 = V2 S 2 . Это уравнение является частным случаем уравнения неразрывности, смысл
которого очевиден: «сколько влилось, столько вылилось». Можно сказать, что теорема о
потоке несжимаемой жидкости выражает общий случай уравнения неразрывности.
Обобщим данную теорему. Пусть в некоторой области движущейся жидкости
имеются источники (и стоки) жидкости. В качестве характеристики источника будем
использовать его расход q : количество (объем) жидкости, вытекающей из источника в
единицу времени. Будем считать, что «сток» тоже источник, расход которого отрицателен.
Из источника жидкость вытекает, в сток стекает: математическая же характеристика для
них едина, но отличается знаком.
«Вторая теорема о потоке несжимаемой жидкости»: Поток несжимаемой
жидкости через любую замкнутую поверхность равен сумме расходов источников,
находящихся внутри поверхности Φ = q . Смысл и доказательство этой теоремы
аналогичны предыдущей: «сколько вливается, столько же выливается». Заметим, что если
внутри рассматриваемой поверхности находятся источники, то поток жидкости через
поверхность не зависит от расположения источников. Подчеркнем – распределение
скоростей (то есть скорости в разных точках), конечно, зависит от положения источников,
но суммарный поток через поверхность полностью определяется суммарным расходом
источников. Если же источник находится вне рассматриваемой поверхности, то он
изменяет распределение скоростей, но не изменяет суммарный поток через
рассматриваемую поверхность.
Применим эту теорему к следующей задаче. Пусть внутри очень
большого объема жидкости находится точечный изотропный источник,
расход которого равен q . Найдем распределение скоростей жидкости возле
источника. Изотропным называется источник, посылающий жидкость во все
стороны одинаково. Реально такой источник можно представить в виде
сферы с большим числом маленьких отверстий, через которые вытекает
жидкость (рис. 109). Понятно, что жидкость будет растекаться от источника во все
стороны одинаково, то есть изотропно. Иными словами, скорость течения жидкости по
модулю одинакова во всех точках, находящихся на одинаковом расстоянии r от
источника, вектор скорости направлен во всех точках радиально от источника. Эти
соображения позволяют нам найти зависимость скорости жидкости от расстояния до
источника.
87
В качестве поверхности, к которой применим теорему о
потоке, используем сферу, радиуса r , в центре которой находится
источник (рис. 110). Выделим на поверхности сферы небольшую
площадку площадью ∆S . На поверхности сферы направление
вектора скорости совпадает с направлением внешней нормали,
поэтому поток жидкости через эту площадку равен ∆Φ = V ⋅ ∆S .
Далее, заметим, что на всех участках сферы, модуль скорости
одинаков. Поэтому суммирование потоков через все участки сферы
сводится к суммированию площадей этих площадок. Таким
образом, суммарный поток через поверхность сферы равен произведению модуля
скорости на площадь сферы Φ = 4πr 2V . С другой стороны, по теореме о потоке, эта
величина равна расходу источника Φ = q . Приравнивая эти выражения 4πr 2V = q ,
получим искомое выражение для скорости жидкости
q
V (r ) =
.
(4)
4πr 2
Отметим, важное обстоятельство: сформулированная теорема о потоке жидкости
справедлива для любой поверхности. Успех в решении этой задачи обусловлен
правильным выбором3 поверхности: во всех точках сферы модуль скорости постоянен, а
угол между скоростью и нормалью равен нулю, именно эти обстоятельства позволили
выразить суммарный поток простой формулой. Для другой поверхности теорема о потоке
также будет выполняться, но в разных точках этой поверхности могут быть разные
скорости, разные углы – поэтому получить выражение для скорости в разных точках
невозможно.
Заметим, что сформулированные теоремы не являются математическими, так как
они явным образом используют физические свойства жидкости, а именно, ее слабую
сжимаемость (т.е. возможностью использовать модель несжимаемой жидкости). Для
газов, приведенные теоремы использовать нельзя, так объемы газов могут изменяться в
широких пределах, поэтому для формулировки подобных теорем необходимо привлекать
физические свойства газов – например, зависимость плотности газа от температуры и
давления.
Таким образом, мы показали, что понятие потока оказывается полезным для описания векторного
поля. В дальнейшем мы будем широко использовать эту математическую конструкцию над векторным
полем для описания физических свойств других реальных полей. В общем случае, если задано векторное
поле, то есть в любой точке пространства с координатами
потоком
вектора
( )
через
малую
площадку
∆S
( x, y , z )
с
r
определен некоторый вектор A , то
нормалью
r
n
называется
r r
∆Φ Ar = A ⋅ n ∆S = A∆S cos α , где α - угол между вектором поля и нормалью к площадке.
величина
В случае поля скоростей движения несжимаемой жидкости поток этого поля имеет наглядный смысл –
объем жидкости, протекающий через поверхность в единицу времени. Для других полей найти смысл
потока может быть затруднительно, в таких случаях к потоку следует относиться как к полезной
математической величине.
3
Произволом в выборе надо пользоваться с умом.
88
7.4 Вихревое движение жидкости. Циркуляция скорости.
Каждому знакомо движение воды в реке – помимо плавного почти однородного
движения, часто встречаются вихри, водовороты. С помощью теорем о потоке нельзя
описать вихревое движение – в вихре поток через любую
замкнутую поверхность равен нулю. Поэтому появление вихрей
не изменяет потоки жидкости через замкнутую поверхность.
Таким
образом,
необходимо
«придумать»
еще
одну
характеристику движения жидкости, зависящую от наличия или
отсутствия вихрей.
Если в движущейся жидкости присутствуют вихри, то
можно найти замкнутую линию, двигаясь вдоль которой все
время «будешь плыть по течению» (Рис. 111). Если же вихри
отсутствуют, то при движении по замкнутой линии на некоторых
участках обязательно придется «плыть против течения». Именно
это отличие позволяет построить требуемую величину,
определяющую наличие участков вихревого движения.
Рассмотрим
произвольную
линию
(совсем
не
обязательно, чтобы это была линия тока). Выделим на этом
r
участке малый участок, определяемый вектором ∆l (рис. 112).
r
Пусть скорость жидкости на этом участке равна V , вычислим
r r
скалярное произведение этих векторов ∆Γ = V ⋅ ∆l = V∆l cos α ,
где α - угол между вектором скорости и касательным вектором к выбранной линии (он
r
совпадает с выделенным малым участком ∆l ). Далее возьмем произвольную замкнутую
r
линию, разобьем ее на малые участки ∆li , на каждом из которых вычислим скалярное
r r
произведение ∆Γ = V ⋅ ∆l = V∆l cos α , и просуммируем их по всем участкам замкнутой
линии (контура)
Γ = V1 ∆l1 cos α 1 + V2 ∆l 2 cos α 2 + V3 ∆l3 cos α 3 + ... =
Vi ∆l i cos α i .
(1)
∑
i
Построенная таким образом, математическая конструкция называется
циркуляцией вектора скорости по заданному контуру L . Построенная величина
может быть как положительной, так и отрицательной, ее знак определяется произвольным
выбором положительного направления обхода контура. Но так уж исторически
сложилось, что в физике положительным принимается направление обхода против
часовой стрелки.
Если в движущейся жидкости вихри отсутствуют, то
циркуляция скорости по любому контуру равна нулю (рис.
113). Если же выбранный контур лежит в области вихря, то
циркуляция вектора скорости будет отлична от нуля. Таким
образом, циркуляция определяет присутствие вихревого
движения. Физические свойства движущейся жидкости
таковы, что ее движение может быть как безвихревым
(ламинарным), так и вихревым (турбулентным). Поэтому
сформулировать какую-либо простую теорему о циркуляции
для движущейся жидкости трудно. Однако математическое
понятие циркуляции широко используется для описания других полей. Для примера
можно указать знаменитую теорему Жуковского, утверждающую, что подъемная сила
крыла самолета пропорциональна циркуляции скорости воздуха по контуру,
охватывающему крыло.
Обратимся еще раз к определению циркуляции по формуле (1). Если в этой
математической конструкции заменить вектор скорости вектором силы, действующей на
89
некоторое тело, то мы увидим, что циркуляция вектора силы является работой силы при
перемещении тела по данному контуру. То есть циркуляция вектора силы имеет явный
физический смысл. Ранее мы определили понятие потенциальности силы (сила, работа
которой не зависит от формы траектории), теперь это же определение можно
сформулировать математически иным образом: сила потенциальна, если ее работа по
любому контуру равна нулю.
И в дальнейшем мы будем встречаться с подобной ситуацией – в некоторых случаях та или иная
конструкция имеет наглядный физический смысл, в других является просто удобной вспомогательной
математической величиной.
Доказано, что законы, определяющие поток векторного поля через любую замкнутую поверхности,
и циркуляцию по любому контуру, однозначно позволяют рассчитывать само векторное поле. Поэтому и
физические законы для реальных полей формулируются именно в такой форме.
7.5 Основные законы гидростатики. Давление. Закон Паскаля. Закон Архимеда.
Наметив в самых общих чертах принципы кинематического описания движения
жидкостей и газов, приступим к рассмотрению основных идей динамики движения, то
есть выяснения причин, того или иного вида движения. Основным понятием динамики
является взаимодействие тел и его характеристика – сила. Следовательно, для
динамического описания движения жидкостей и газов необходимо рассмотреть
взаимодействие различных частей жидкой среды между собой. Как мы уже отмечали, эти
силы обусловлены межмолекулярными взаимодействиями, их полное описание
чрезвычайно сложно, но сейчас нам нет необходимости досконально знать законы этих
взаимодействий, достаточно принять во внимание, что при деформации жидкости (то есть
изменении расстояния между молекулами) возникают силы упругости.
Помимо межмолекулярных сил (сил давления, обусловленных деформацией
жидкости), на жидкость могут действовать и внешние силы, например, гравитационные (в
частности, сила тяжести), инерционные, электрические, магнитные и т.д. Имеет смысл,
разделить эти внешние силы на две группы – объемные, действующие, на все части
жидкости, и поверхностные, действующие только на поверхность жидкости со стороны
окружающих тел (например, стенок сосуда).
Пусть жидкость находится в состоянии покоя. В качестве исходных «аксиом»
примем законы динамики Ньютона и очевидный экспериментальный факт - жидкость
обладает свойством текучести. Полученные в данном разделе результаты в равной мере
применимы и к газам.
Рассмотрим, какие следствия можно извлечь из этих «аксиом».
1. Сила, с которой покоящаяся жидкость
действует на стенки сосуда, направлена
перпендикулярно к этим стенке (рис. 114).
Докажем это утверждение методом «от
противного». В пусть в некоторой части сосуда,
r
сила давления F Д , действующая на стенку,
направлена под некоторым (не прямым) углом к
последней. По третьему закону Ньютона, стенка
r
действует на жидкость с силой F , равной по величине и
r
r
противоположной по направлению F = − F Д . Разложим эту силу
r
на нормальную (направленную перпендикулярно стенке) Fn и
r
тангенциальную (направленную по касательной к стенке) Fτ
составляющие (рис. 115). При наличии тангенциальной силы,
действующей на жидкость, жидкость, вследствие текучести,
придет в движение. В состоянии равновесия таких сил быть не
может. Следовательно, силы взаимодействия стенки и жидкости нормальны к стенке.
90
2. Силы, действующие на границу мысленно выделенного объема
неподвижной жидкости, перпендикулярны этой границе (рис. 116).
Это утверждение доказывается аналогично предыдущему, методом от
противного.
Итак, вопрос о направлении сил взаимодействия жидкости с
сосудом и различных частей жидкости, решается однозначно – эти
силы направлены по нормали к границе раздела. Если внутри жидкости выделить
некоторую малую площадку, то модуль силы, действующей на одну сторону этой
площадки, не зависит от ее ориентации. Это свойство внутренних сил позволяет ввести
скалярную силовую характеристику взаимодействий внутри жидкости – давление.
Строго говоря, силы взаимодействия между различными частями жидкости изменяются от точки к
точке, поэтому изменение ориентации не малой площадки приведет к изменению силы, действующей на
нее. Для малой4 же площадки можно пренебречь изменением сил взаимодействия в ее пределах. Поэтому
модуль рассматриваемой силы в этом случае оказывается пропорциональной площади. Следовательно,
отношение модуля силы к площади площадки является характеристикой сил упругости внутри жидкости.
Давление – отношение модуля силы, действующей на выделенную малую площадку,
к площади этой площадки
∆F
p=
при ∆S → 0 .
(1)
∆S
Как мы уже отмечали, жидкость может быть, как сжата, так и растянута, поэтому
силы давления (силы упругости), оставаясь нормальными, могут быть направлены в
разные стороны от границы жидкости. Для указания направления можно указывать знак
давления. Принято считать давление положительным, если сила давления жидкости
направлена наружу от рассматриваемого объема, что соответствует сжатой жидкости, в
случае же растянутой жидкости силы упругости направлены внутрь жидкости, поэтому
давление такой жидкости считается отрицательным.
Понятно, что сила, действующая на площадку, может зависеть от ее положения
внутри жидкости, поэтому и давление может изменяться при переходе от одной точке
объема жидкости к другой. В этом смысле, давление следует рассматривать как точечную
характеристику, то есть как функцию координат p ( x, y, z ) .
Конечно, измерить давление «в данной точке» измерить невозможно – измерению поддается только
сила, действующая на площадку конечной площади. Кроме того, бессмысленно говорить о давлении на
площадях, сравнимых с размерами отдельной молекулы. Однако с точки зрения простоты математического
описания удобней рассматривать давление именно как функцию координат, понимая физическую
ограниченность этого понятия.
Учитывая, что сила, действующая на малую
площадку, направлена по нормали к площадке, а ее
модуль выражается из формулы (1), вектор силы
r
r
r
можно записать в виде ∆F = p∆Sn , где n единичный
вектор нормали к площадке. Для вычисления
суммарной силы давления на некоторую поверхность
внутри
жидкости,
необходимо
разбить
эту
поверхность на малые участки (рис. 117), вычислить
силу, действующую на каждую площадку, и
r
r
просуммировать все эти силы F =
pi ∆S i ni .
∑
i
Продолжим рассмотрение следствий из условий равновесия жидкости.
3. Векторная сумма внешних сил, действующих на любую мысленно выделенную часть
неподвижной жидкости, равна нулю.
Это утверждение просто повторяет общее условие равновесия любого тела, в том
числе и жидкого.
4
Точнее следует говорить о бесконечно малой площадке.
91
4. При отсутствии объемных сил, действующих на жидкость, давление во всех точках
объема одинаково.
Для доказательства этого положения, мысленно выделим
внутри жидкости произвольно ориентированный узкий цилиндр
(рис. 118). Так как жидкость в выделенном объеме находится в
покое, то силы, действующие на основания цилиндра, равны по
r
r
модулю и противоположны по направлению F1 = − F2 . Из этого
соотношения и определения давления следует, что давления в
точках оснований цилиндров равны. Аналогичные рассуждения справедливы для любого
цилиндра, следовательно, давление во всех точках жидкости одинаково.
Справедливо и обратное утверждение.
5. Если давление жидкости во всех точках одинаково, то суммарная сила, действующая
на произвольную замкнутую поверхность, полностью находящуюся внутри жидкости,
равна нулю.
Выделим внутри объема жидкости произвольную
замкнутую поверхность. На каждый малый участок
поверхности
действует сила давления
жидкости,
направленная перпендикулярно данному участку. Докажем,
что сумма проекций сил давления на произвольное
направление (например, ось X ) равна нулю. Для этого
разобьем выделенную часть объема на узкие цилиндры,
боковые поверхности которых параллельны выделенной
оси (рис. 119). На основания этих цилиндров действуют
силы давления, равные F1 = pS1 , F2 = pS 2 , где S1 , S 2 площади оснований цилиндров. Проекции сил на
выбранное
направление
оси
равны
F1x = pS1 cos α 1 , F2 x = − pS 2 cos α 2 , где α 1 , α 2 - углы между
нормалями к основаниям и осью X . Теперь заметим, что S1 cos α 1 = S 2 cos α 2 = S 0 , где
S 0 - площадь поперечного сечения выбранного цилиндра, поэтому F1x + F2 x = 0 .
Аналогичное соотношение справедливо для всех цилиндров, на которые разбито тело,
поэтому сумма проекций сил на ось X равна нулю. Так как ось X выбрана произвольно,
то сумма проекций сил давления на любую ось равна нулю, следовательно, и векторная
сумма рассматриваемых сил также равна нулю.
6. (Закон Паскаля). Давление на поверхность жидкости, произведенное внешними
силами, передается жидкостью во все стороны одинаково.
Данный закон справедлив и в том случае, когда на жидкость действуют объемные силы.
Пусть жидкость находится в сосуде под поршнем (рис. 120). Приложим к
r
поршню дополнительную нормальную силу F . Под действием этой
силы жидкость дополнительно сожмется, что приведет к увеличению
давления. В состоянии равновесия эта дополнительная сила будет
скомпенсирована равным увеличением силы давления на поршень со
стороны жидкости. Следовательно, увеличение давления жидкости
F
, где S 0 - площадь
непосредственно под поршнем будет равно ∆p0 =
S0
поршня.
Выделим внутри жидкости произвольную замкнутую
поверхность, часть которой совпадает с поверхностью поршня. В
r
состоянии равновесия сумма объемных сил Fоб . , действующих на выделенную часть
r
r
жидкости, и поверхностных сил давления Fпов =
pi ∆S i n равна нулю:
∑
i
92
r
Fоб . +
∑
r r
pi ∆S i n = 0
(2)
i
Дополнительная сила давления на часть выбранной поверхности под поршнем
должна быть скомпенсирована увеличением поверхностных сил давления на остальную
поверхность. Обозначим увеличение давления вблизи части ∆S i поверхности - ∆pi . В
состоянии равновесия должно выполняться соотношение, аналогичное (2)
r
r
( pi + ∆pi )∆S i nr = 0
Fоб . +
(3)
∑
i
Учитывая, что суммарная объемная сила не изменилась, из (2), (3) следует, что
соотношение
r r
∆p i ∆S i n = 0 ,
∑
i
должно выполняться для любой поверхности внутри объема жидкости, что возможно
только в том случае, если величины ∆pi одинаковы во всех точках жидкости, то есть
F
∆pi = ∆p 0 =
. Отметим, что закон Паскаля можно интерпретировать следующим
S0
образом: в состоянии равновесия изменение давления в одной точке жидкости
приводит к равному изменению давления во всех остальных точках жидкости.
Существенным в данной формулировке является упоминание о состоянии равновесия, потому, что
при увеличении давления в некоторой точке жидкости, требуется некоторый промежуток времени, чтобы
произошло установления равновесия в остальных частях объема жидкости, иными словами, возмущение
жидкости распространяется внутри объема с конечной скоростью. Позднее мы покажем, что эта скорость
есть скорость распространения упругих волн (т.е. звука) в данной жидкости.
Важными
следствием закона Паскаля является,
так называемый,
«гидростатический парадокс» - давление жидкости на дно сосуда не зависит от формы
сосуда, который проявляется в свойствах сообщающихся сосудов. Закон Паскаля также
является теоретическим обоснованием таких устройств как гидравлический пресс, сифон
и т.д.
7. В поле тяжести земли давление жидкости на глубине h определяется по формуле
p = ρgh ,
(4)
где ρ - плотность жидкости, g - ускорение свободного падения. Давление, определяемое
формулой (4), называется гидростатическим.
Для вывода этой формулы достаточно выделить внутри объема жидкости
вертикальный цилиндр высотой h , верхнее основание которого площадью S находится
на свободной поверхности жидкости, и рассмотреть условия его равновесия. Объемные
силы, действующие на жидкость внутри выделенного цилиндра (в данном случае это сила
тяжести mg = ρgV = ρghS ) уравновешивается силой давления на нижнее основание
цилиндра pS . Из условия равенства этих сил следует формула (4).
Заметим, что формула (4) описывает только ту часть давления, которая обусловлена силой тяжести,
действующей на жидкость. В общем случае полное давление на глубине h будет равно сумме
гидростатического давления и внешнего давления на поверхность жидкости (например, атмосферного
давления).
8. (Закон Архимеда). На погруженное в жидкость тело, действует
выталкивающая сила, равная суммарной объемной силе,
действующей на жидкость в объеме тела.
Доказательство этого закона достаточно просто. По своей
природе выталкивающая сила есть векторная сумма сил давления
жидкости на поверхность тела (рис.121). Следовательно, эта сила
определяется
распределением
давления
жидкости
вблизи
поверхности тела. Мысленно уберем тело из жидкости, оставив
только его «оболочку», которую заполним той же жидкостью. От
93
такой замены суммарная сила давления на поверхность не изменится. С другой стороны,
очевидно, что жидкость в объеме тела, находящаяся в такой же жидкости будет
находиться в равновесии. Поэтому суммарная сила давления будет равна по величине и
противоположна по направлению объемной силе, действующей на жидкость в объеме
тела.
В частном случае, если единственной объемной силой является сила тяжести, и при
постоянной плотности жидкости ρ , выталкивающая сила (сила Архимеда FАр ) по
модулю равна силе тяжести, действующей на жидкость в объеме тела V
противоположна ей по направлению:
r
r
FАр = ρgV или в векторной форме FАр = − ρgV .
и
Заметим, что выталкивающая сила появляется только в том случае, когда давление внутри жидкости
различно в различных точках. В случае постоянного давления (каким бы большим оно не было) суммарная
сила давления равна нулю. Различие давлений обусловлено только объемными силами, действующими на
жидкость. Поверхностные силы, как было нами показано, не могут привести к возникновению разности
давлений в различных точках жидкости. Допустим, что жидкость находится под поршнем – увеличения
силы давления на поршень не приведет к увеличению выталкивающей силы, действующей на погруженное
в жидкость тело.
В общем случае выталкивающая сила может описываться более сложными формулами, которые
могут учитывать изменение плотности жидкости, изменение ускорения свободного падения, как по
величине, так и по направлению, присутствие других объемных сил – инерционных, электрических,
магнитных и т.д.
94
7.6 Движение жидкости - гидродинамика. Течение жидкости по трубам.
Движение жидкости или газа подчиняется всем общим законом механики –
законам Ньютона, законам сохранения энергии, импульса, момента импульса. Однако,
применение этих общих законов встречает значительные трудности обусловленных рядом
причин. Во-первых, жидкость обладает бесконечным числом степеней свободы, что
приводит к необходимости перехода от дискретного к непрерывному описанию. Вовторых, свойства жидкостей (и особенно газов) изменяются при изменении внешних
воздействий. Так могут изменяться плотности, вязкости, сжимаемости жидких и
газообразных сред при изменении давления, температуры и т.д. В-третьих, изменения
параметров среды в одной точке приводит к изменению параметров в других точках не
мгновенно, а через некоторые промежутки времени, обусловленные конечностью
скоростей распространения упругих волн, теплоты и т.д. Эти обстоятельства приводят к
тому, что наука о движении жидкостей и газов (гидродинамика и аэродинамика) является
одной из самых сложных в математическом плане.
Мы рассмотрим существенно упрощенную проблему - описание стационарного
течения жидкости, то есть такого течения, когда скорости (поле скоростей) в различных
точках могут быть различными, но не изменяться с течением времени. Такое течение
жидкости также называется стационарным. Подчеркнем, что при стационарном течении в
некоторых областях жидкость может двигаться с ускорением, ведь при переходе от точки
к точке скорость движения конкретной частицы жидкости может изменяться. Кроме того,
ограничим наше рассмотрение моделью несжимаемой жидкости. При взаимодействии
движущейся жидкости с твердыми телами, а также при относительном движении слоев
жидкости, появляются силы вязкого трения. Если роль этих сил невелика, если ими
можно пренебречь, то используется модель идеальной жидкости – жидкости, не
обладающей вязкостью. Будьте внимательны, так как в данном разделе используются
модели как идеальной, так и вязкой жидкостей.
По-прежнему, мы не рассматривая конкретные физические свойства жидкости,
посмотрим какие следствия можно извлечь из общих законов динамики.
7.7 Давление в движущейся жидкости.
Уточним понятие давления на случай движущейся жидкости. В случае
неподвижной жидкости давление обусловлено сжатием или растяжением жидкости.
Возникающие при этом силы упругости, действующие на произвольную площадку внутри
жидкости, не зависят от ориентации последней. Для иллюстрации высказанного
утверждения проведем такой эксперимент (хотя бы
мысленный).
В качестве измерителя давления будем использовать
манометр, представляющий собой маленькую жесткую
цилиндрическую коробку, одно из оснований которой способно
деформироваться (рис. 122). Это основание назовем
мембраной. Прогиб мембраны служит мерой давления
жидкости на мембрану. Можно присоединить к коробке
измерительную трубку. Заполнив коробку и частично трубку
некоторой жидкостью, получим измеритель давления –
манометр, высота уровня жидкости в трубке пропорциональна силе давления на
мембрану. Если площадь мембраны мала, то описанный прибор позволяет измерять
давление «в точке». При погружении такого манометра в неподвижную жидкость
показания будут одинаковы при любой ориентации мембраны.
Иное дело – показания манометра при его погружении его в движущуюся
жидкость. Понятно, что высота поднятия жидкости в трубке будет максимальна, если
плоскость мембраны перпендикулярна скорости движения жидкости (рис. 123). В этом
случае сила, действующая на мембрану со стороны жидкости, будет зависеть не только от
95
степени сжатия жидкости, но и от ее скорости. Та часть силы
давления, которая зависит от скорости потока, называется
динамическим напором. Его появление связано с тем, что наш
измерительный прибор будет возмущать поток жидкости, заставляя
часть жидкости изменять направление скорости, что неизбежно
приводит к появлению дополнительной силы давления. Если же
расположить мембрану так, чтобы вектор скорости жидкости был
направлен параллельно (по касательной, тангенциально)
измерительной мембране, то возмущение движения жидкости
может быть пренебрежимо малым, поэтому при таком положении манометра, его
показания будут соответствовать давлению, обусловленному исключительно сжатием
(или растяжением) жидкости. Измеренное таким способом давление мы и будем
подразумевать в дальнейшем изложении.
7.8 Распределение давления в идеальной жидкости, движущейся по горизонтальной
трубе.
Рассмотрим распределение давления в горизонтальной цилиндрической трубе,
полностью заполненной жидкостью. Для этого расположим на трубе ряд измерительных
манометров, высота уровня жидкости в которых будет показывать величину давления в
данном месте трубы.
Если жидкость неподвижна, то давление
жидкости (и соответственно высоту жидкости в
измерительных трубках) будут одинаковы во всех
точках трубы (рис. 124).
Для идеальной жидкости (то есть при
пренебрежении силами вязкого трения) давление
внутри горизонтальной трубы остается постоянным и
при равномерном движении жидкости – в этом случае
нет необходимости преодолевать силы сопротивления.
Исследуем теперь распределение давлений внутри трубы переменного сечения при
движении идеальной жидкости. Пусть труба состоит из двух сочлененных частей,
площади поперечных сечений которых равны S1 и S 2 (рис. 125). В такой трубе при
движении даже идеальной жидкости в области сочленения должна существовать область
изменения
давления.
Действительно,
согласно
уравнению
неразрывности
скорости
движения
жидкости в разных частях трубы связаны
соотношением v1 S1 = v 2 S 2 . Поэтому, при переходе
жидкости из более широкой в более узкую части трубы
скорость жидкости должна возрастать, что может
произойти только благодаря действию силы,
обусловленной разностью давлений в узкой и широкой
частях. Причем давление в более широкой части
должно быть выше.
Для упрощения расчета разности давлений представим себе, что в обеих частях
трубы расположены легкие подвижные поршни. Кроме того, пренебрежем силами вязкого
трения, то есть будем считать жидкость идеальной. Пусть поршень в левой части трубы
сместился на расстояние h1 , тогда поршень в правой части сместится на расстояние h2 . Из
условия несжимаемости жидкости смещения поршней связаны соотношением
h1 S1 = h2 S 2 = V , где V объем жидкости прошедший через поперечное сечение трубы. На
левый поршень действует внешняя сила F1 = p1 S1 , работа совершенная этой силой при
смещении поршня будет равна A1 = p1 S1 h1 . Правый поршень совершит работу (по
96
перемещению жидкости за поршнем) A2 = p 2 S 2 h2 . Кроме того, при перемещении
жидкости возрастает кинетическая энергия жидкости, прошедшей через место
ρS 2 h2 2 ρS1 h1 2
сочленения. Увеличение кинетической энергии равно ∆E k =
v2 −
v1 . По
2
2
закону сохранения энергии работа, совершенная над левым поршнем внешней силой,
равна сумме работы, совершенной правым поршнем над «внешней» жидкостью, и
изменению кинетической энергии системы: A1 = A2 + ∆E k . С учетом условия постоянства
объема жидкости, это уравнение приобретает вид
ρv 2 ρv 2
(1)
p1 − p 2 = 2 − 1 .
2
2
Таким образом, мы получили величину скачка давления в месте сочленения трубы,
которая квадратично возрастает с ростом скорости течения.
На
рисунке
126
схематически
показано
распределение давления вдоль оси трубы, скачок давления
происходит в области сочленения. При скорости движения
равной нулю, давление постоянно во всех точках жидкости.
Из уравнения (1) можно вычислить скорости движения и
расход жидкости в зависимости от приложенной разности
давлений
2S12 S 22 ∆p
⋅
.
(2)
S12 − S 22 ρ
Как следует из полученной формулы, расход жидкости не пропорционален приложенной
разности давлений – так, для увеличения расхода жидкости в два раза, разность давлений
должна быть увеличена в четыре раза.
Q = S1v1 = S 2 v 2 =
Задания для самостоятельной работы.
1. Из формулы (1) следует, что скачок давления не зависит от направления движения
жидкости. Объясните полученный результат. В какую же сторону будет двигаться
жидкость, если к концам трубы приложить некоторую разность давлений?
2. Нарисуйте силы, действующие на движущуюся жидкость в трубе переменного
сечения со стороны стенок трубы.
3. Из формулы (2) следует, что при выравнивании площадей поперечного сечения труб
( S 2 → S1 ) расход жидкости стремится к бесконечности. Объясните этот результат.
Можно ли применять эту формулу при S 2 > S1 ?
7.9 Уравнение Бернулли.
Уравнение (1) предыдущего раздела можно
записать в форме уравнения
2
2
ρv
ρv
сохранения
p1 + 1 = p 2 + 2 = const . Можно показать, что такое уравнение
2
2
справедливо для идеальной несжимаемой жидкости при ее движении по горизонтальной
трубе переменного сечения. Иными словами величина
ρv 2
p+
= const
(1)
2
остается постоянной в любом сечении трубы.
97
Задание для самостоятельной работы.
Покажите, что при движении идеальной несжимаемой
жидкости по не горизонтальной трубе в любом поперечном
сечении остается постоянной величина
ρv 2
p + ρgh +
= const ,
(2)
2
h - высота, на которой находится центр
где
рассматриваемого сечения, g - ускорение свободного
падения (рис. 127).
Уравнение (12) или в более общей форме (13) впервые получено Даниилом
Бернулли и носит его имя. Это одно из основных уравнений динамики идеальной
жидкости, справедливое для любого не турбулентного движения идеальной жидкости. По
своей же физической сути оно выражает закон сохранения механической энергии для
движущейся жидкости.
Из уравнения Бернулли следует, что давления жидкости меньше в тех местах, где
скорость движения больше. Однако нельзя утверждать, что увеличение скорости является
причиной уменьшения давления. Наоборот – уменьшение давления приводит к
увеличению скорости. Как и прежде – в установившемся режиме устанавливается такое
распределения давления, которое обеспечивает стационарное течение. При учете вязкого
трения уравнение Бернулли оказывается несправедливым, так как часть механической
энергии «теряется», переходит в тепловую. Однако и в этом случае связь между
давлением и скоростью качественно остается прежней: в местах большей скорости
движения давления должно быть меньше.
Задания для самостоятельной работы.
1. Какой физический смысл имеют величины ρgh и
ρv 2
?
2
2. Открытый вертикальный цилиндрический сосуд заполнен жидкостью до высоты h . В
дне сосуда проделывают небольшое отверстие. Используя уравнение Бернулли,
покажите, что скорость истечения жидкости из отверстия определяется формулой Э.
Торричелли v = 2 gh .
7.10 Плотность энергии движущейся жидкости.
Как и всякое движущееся тело, движущаяся жидкость обладает кинетической
энергией.
Выделим внутри движущейся жидкости малый
5
объем ∆V (рис. 128), в котором заключена масса жидкости
∆m = ρ∆V . Если в пределах этого выделенного объема
жидкость движется со скоростью v , то она обладает
ρ∆V ⋅ v 2
кинетической энергией ∆W =
. Введем «точечную»
2
энергетическую характеристику – для этого разделим
кинетическую энергию на объем, в котором эта энергия
заключена
∆W ρv 2
=
.
(1)
w=
∆V
2
5
Следите внимательно за обозначениями физических величин – их так много, что не хватает различных
букв, в этом разделе символ V означает объем, а v - скорость.
98
Полученная физическая величина называется объемной плотностью кинетической
энергии – энергии заключенной в единице объема движущейся жидкости.
В неоднородных полях скоростей для строго определения плотности энергии «в данной точке»,
необходимо совершить обычный предельный переход ∆V → 0 , не забывая, что физический смысл имеет
только произведение w∆V .
Таким образом, мы получаем еще одну характеристику поля скоростей
движущейся жидкости. В движущейся жидкости энергия переносится от одной точки к
другой. Характеристикой переноса энергии служит вектор плотности потока энергии,
который определяется как произведение плотности энергии на скорость движения
жидкости
r
r
J = wv .
(2)
Эта векторная физическая величина определена в каждой пространственной точке,
поэтому с математической точки зрения также описывается векторным полем, для
которого определены все математические операции над векторным
полем.
Поток (как математическая операция) этого вектора через
r
площадку ∆S , положение которой определяется вектором нормали n
r r
∆Φ j = J ⋅ n∆S
имеет смысл энергии, которая перетекает через площадку в единицу
времени (рис. 129).
В принципе, на основании физических законов можно сформулировать ряд теорем, определяющих
как плотность энергии, так и плотность потока энергии. При описании движения твердых тел пользуются
как динамическим (основанном на законах Ньютона), так и энергетическим подходами. Аналогичная
ситуация и при описании движении жидкостей, правда в последнем случае уравнения гораздо сложнее и
решаются значительно реже.
99
7. 10 Движение вязкой жидкости по горизонтальной трубе.
Если по горизонтальной трубе постоянного сечения будет протекать жидкость
реальная жидкость, для которой нельзя пренебречь силами вязкого трения, то давление в
трубе не будет постоянным, произойдет перераспределение давления, которое будет
существенно зависеть от свойств жидкости. Рассматривая проблемы возникновения сил
вязкого трения, мы упоминали о такой характеристике жидкости
как вязкость. Сейчас мы уточним это понятие.
Рассмотрим плоский поток жидкости, в пределах которого
r
скорость v ( z ) различных слоев которого изменяется, оставаясь
параллельной основанию потока (рис. 130). В реальной жидкости
различные слои жидкости, имеющие разные скорости будут
взаимодействовать между собой, то есть между слоями жидкости
благодаря межмолекулярным взаимодействиям будут возникать
силы вязкого трения – более медленный слой будет тормозить более быстрый.
Важно
отметить, что эти силы направлены параллельно слоям
жидкости, то есть тангенциально к границе раздела (рис.
131). Величина этих сил также зависит от распределения
r
скорости v ( z ) , где z - координата, ось которой направлена
перпендикулярно скорости течения.
Силы
вязкости
определяется
законом
Ньютона6:
тангенциальная сила вязкого трения между движущимися слоями жидкости приходящаяся на единицу
площади соприкосновения равна
F =η
∆v
,
∆z
в этой формуле коэффициент пропорциональности η - полностью определяется свойствами жидкости и
называется ее вязкостью. Вязкость может изменяться в широких пределах, она мала для легко подвижных
жидкостей, таких как вода, бензин, эфир, и велика для малоподвижных жидкостей таких как масло, мед,
смола и т.д. В целом строгое понятие вязкости вполне соответствует обычным представлениям о вязких и
маловязких жидкостях. Модель движущейся жидкости, в рамках которой пренебрегают вязкостью,
называется идеальной жидкостью.
Обратите внимание – в случае неподвижной жидкости силы взаимодействия
между слоями всегда нормальны, в движущейся жидкости появляются тангенциальные
составляющие!
Важно отметить, что силы вязкости не являются консервативными, наличие этих
сил, их работа приводит к переходу механической энергии в тепловую, к потерям
механической энергии.
При стационарном движении жидкости трубы на нее со
стороны стенок будут действовать тормозящие силы вязкого
трения. Поэтому скорость движения жидкости в поперечном
сечении будет различной, установится некоторое стационарное
распределение скоростей – скорость максимальна в центре трубы
и приближается к нулю вблизи стенок (рис. 132).
Для расчета сил вязкого трения, действующих на жидкость
необходимо, прежде всего, найти распределение скоростей жидкости внутри трубы
(используя закон вязкого трения), после чего можно вычислить силу сопротивления
движению, расход жидкости и так далее.
Для круговой цилиндрической трубы эта задача была решена французским
физиком Ж. Пуазейлем, который установил, что расход7 жидкости пропорционален
6
И. Ньютон является автором многих законов и не только в механике!
Напомним, расходом называется объем жидкости, который протекает через поперечное сечение трубы в
единицу времени.
7
100
разности давлений на концах трубы ∆p , четвертой степени радиуса трубы, обратно
пропорционален ее длине
r4
Q = K ∆p ,
(1)
l
коэффициент пропорциональности зависит от вязкости жидкости. Если поперечный
профиль отличен от кругового, то формула Пуазейля несколько видоизменяется, но
расход жидкости остается пропорциональным разности давлений на концах трубы
∆p
,
(2)
Q=
R
1
в этой формуле коэффициент пропорциональности обозначен
, тогда величина R R
называется гидродинамическим сопротивлением. Гидростатическое сопротивление
участка трубы длиной ∆l можно представить в виде R = r∆l , где r - сопротивление
единицы длины трубы, зависящее от вязкости жидкости, размеров и формы поперечного
сечения трубы. С увеличением площади поперечного сечения гидродинамическое
сопротивление уменьшается.
Внимательно посмотрим на формулу (2) – она достойна того. Если площадь
поперечного сечения трубы постоянна, то скорости движения жидкости не изменяются
вдоль трубы, то есть любая частица жидкости движется с постоянной скоростью, без
ускорения. Тем не менее, для того чтобы жидкость двигалась с постоянной скоростью, к
ней необходимо прикладывать постоянную внешнюю силу, то есть создавать разность
давлений на концах трубы. Кажущееся противоречие легко снимается, если принять во
внимание силы вязкого трения, действующие между различными слоями жидкости.
Фактически внешнюю силу необходимо прикладывать, чтобы преодолеть силы вязкого
трения. Конечно, суммарная сила, действующая на любую часть равномерно движущейся
жидкости равна нулю.
Ситуация аналогична движению тела в вязкой среде, когда на
него действует сила сопротивления (рис. 133), пропорциональная
скорости движения Fсопр. = βv . Если к телу приложить постоянную
F , то тело будет двигаться со скоростью,
F
пропорциональной внешней приложенной силе v = .
внешнюю силу
β
Итак, при движении вязкой жидкости по трубе внутри устанавливается
распределение давлений – давление линейно падает при
смещении вдоль направления движения жидкости
(рис.134). Подчеркнем, что в данном случае,
приложенная разность давлений является причиной
движения жидкости – при стационарном движении
происходит установление нужного распределения
давлений вдоль трубы.
Можно
сказать, что для преодоления
гидростатического сопротивления
R
необходимо
приложить разность давлений (или на сопротивлении
происходит падение давления) ∆p = RQ .
Направим координатную ось X вдоль трубы. Пусть в точке с координатой x = 0
Применим формулу Пуазейля для слоя жидкости от x = 0 до
давление равно p 0 .
произвольного значения координаты x . Из формулы (15) следует, что
p 0 − p( x ) = QR = Qrx ,
где p (x ) -давление жидкости в сечении с координатой x .
101
Таким образом, распределение давления вдоль трубы при движении вязкой
жидкости представляет собой линейную зависимость
p ( x ) = p1 − Qrx .
Коэффициент наклона графика данной
∆p
зависимости
возрастает с ростом скорости течения
∆x
жидкости и гидродинамического сопротивления (рис.135).
В установившемся режиме скорость8 изменения
∆p
давления вдоль трубы
остается постоянной вдоль трубы.
∆x
∆p
имеет явный физический смысл. Величина F = S∆p - есть
Заметим, что отношение
∆x
суммарная сила давления, действующая на слой жидкости толщиной ∆x ; следовательно,
∆p
F
=
- есть суммарная сила давления, действующая на единицу объема
величина f =
S∆x ∆x
жидкости – то есть объемная плотность силы давления.
Выделим в движущейся жидкости небольшой параллелепипед, одно из ребер
которого длиной l параллельно скорости жидкости, площадь грани
перпендикулярной скорости равна S (рис. 136). Пусть разность
давлений между противоположными гранями этого объема равна ∆p ,
тогда произведение ∆F = ∆pS равно суммарной силе давления на
жидкость внутри выделенного объема, а величина ∆A = ∆pSl равна
работе, которую совершают силы давления внутри данного объема.
∆A
= ∆p с одной стороны разность давлений, с
Наконец, отношение
Sl
другой – работа сил давления, которая совершается при перетекании жидкости через
данный объем.
Полученное распределение давления соответствует стационарному течению жидкости. Качественно
рассмотрим процесс установления движения. Пусть длинная горизонтальная труба полностью заполнена
жидкостью, с одной стороны внутри трубы расположен поршень (рис. 137). В некоторый момент времени к
поршню начинают прикладывать постоянную силу. Вся жидкость в трубе
сразу прийти в движение не сможет. Непосредственно перед поршнем
возникнет область сжатия, которая начнет распространяться по трубе,
приводя в движение все более удаленные области жидкости внутри
трубы. Скорость распространения области сжатия совпадает со
скоростью звука в жидкости. Наконец, по прошествии некоторого
небольшого промежутка времени в трубе установится такое распределение давления, которое обеспечит
постоянство скорости вдоль трубы. Именно этот установившийся режим мы и рассматриваем.
Задание для самостоятельной работы.
1. Представьте расход жидкости в виде Q = v S , где S - площадь поперечного сечения
трубы, v - усредненная по поперечному сечению скорость течения. Используя формулу
Пуазейля для круглой трубы (1), выразите среднюю скорость течения жидкости через
разность давлений, а также через объемную плотность силы давления. Что вам
напоминают полученные формулы?
2. Постройте примерный график распределения давления в трубе переменного сечения
(состоящей из двух сочлененных труб разного радиуса) при движении в ней вязкой
жидкости.
8
В данном виду имеется в виду изменение давления по ходу трубу, а не скорость изменения со временем.
102
7.11 Движение вязкой жидкости по горизонтальному замкнутому контуру.
Безусловно, для обеспечения постоянного движения вязкой жидкости необходим
источник энергии, необходимо устройство для поддержания постоянной разности
давления на концах трубы.
Для перекачки жидкости таким устройством
является насос. Рассмотрим контур, состоящий из
замкнутой трубы с постоянным сечением,
подключенной к насосу (рис. 138). Включенный
насос создает между своим входом и выходом
некоторую разность давлений. Назовем напором
насоса разность давлений между входом и выходом
при неподвижной жидкости и обозначим его P .
При движении жидкости по трубе из-за сил вязкого трения происходит падение давления,
величина которого может быть рассчитана по формуле Пуазейля ∆p = QR , где Q - расход
жидкости, R - гидродинамическое сопротивление трубы. При прохождении через насос
на жидкость также действуют силы вязкого трения, поэтому разность давлений между
входом и выходом насоса в этом случае окажется меньше напора, и будет уменьшаться с
ростом скорости движения жидкости. По аналогии с падением давления в трубе можно
говорить о падении давления в насосе ∆p 0 , величины равной разности давлений
необходимой для преодоления сил вязкого трения при прохождении через насос. Это
падение давления также можно считать пропорциональным скорости движения жидкости,
или ее расходу. Таким образом, можно ввести гидродинамическое сопротивление насоса
R0 из условия ∆p 0 = QR0 . Тогда разность давлений между концами трубы равно
∆p = P − ∆p 0 .
Схематически распределение давления в контуре
изображено на рисунке 139. В насосе давление
повышается в направлении движения жидкости и
убывает по ходу жидкости в трубе.
Понятно, что разность давлений (напор),
создаваемая насосом, равна сумме падений давления в
трубе и насосе
P = ∆p + ∆p 0 .
(1)
Из этих соотношений можно выразить расход жидкости
в данной системе
P
Q=
,
(2)
R + R0
расход жидкости в замкнутом контуре равен
отношению напора насоса к полному гидродинамическому сопротивлению контура.
Полученному соотношению можно придать и энергетическое истолкование. Как
известно, мощность (работа в единицу времени), развиваемая силой, равна произведению
силы на скорость движения тела N = Fv . При движении жидкости по трубе, сила,
действующая на жидкость равна F = ∆pS ( S - площадь поперечного сечения трубы).
Поэтому мощность сил давления вычисляется по формуле N = Fv = ∆pSv = ∆pQ , и равна
произведению разности давлений на расход жидкости Q = Sv . Используя формулу
Пуазейля, связывающее расход жидкости с разностью давлений, выражение для
мощности течения можно записать в нескольких формах
(∆p )2 .
N = ∆pQ = Q 2 R =
(3)
R
103
Подчеркнем еще одно существенное обстоятельство – при стационарном течении
суммарная сила давления по модулю равна суммарной силе вязкого трения. Поэтому
формулы (3) также выражают мощность сил сопротивления. Действие этих сил
сопротивление приводит к переходу механической энергии в тепловую, поэтому эти же
формулы определяют мощность теплоты, выделяющейся при прохождении жидкости.
Аналогично, произведение напора на расход равно мощности, развиваемой насосом.
Умножим равенство (1) на расход жидкости
PQ = ∆pQ + ∆p 0 Q .
(4)
Смысл полученного соотношения – мощность, развиваемая насосом равна, суммарной
мощности сил вязкости. Работа, совершенная насосом, равна тепловой энергии
выделяющейся при протекании жидкости. Иными словами – очередное проявление закона
сохранения энергии.
Задание для самостоятельной работы.
Рассмотрите движение идеальной жидкости
по системе, изображенной на рисунке 140.
Найдите расход жидкости, если напор насоса
равен P , площадь поперечного сечения трубы
постоянна и равна S , плотность жидкости
ρ.
104
§ 8. Электростатические взаимодействия. Электрический заряд. Закон Кулона.
В большинстве учебников физики данный раздел начинается с банальной фразы
«еще древние греки заметили, что палочка янтаря, потертая шерстью, притягивает мелкие
предметы – перышки, кусочки коры и т.д.» Действительно, в жизни нам приходится
встречаться с особым видом взаимодействий тел – электрическими взаимодействиями1.
Внутренняя природа этих взаимодействий не известна до сих пор, поэтому нам остается
только признать объективную реальность – некоторые тела обладают способностью
взаимодействовать друг с другом также как «кусочки янтаря, потертые шерстью».
Безусловно, со времен Древней Греции наши знания об окружающем мире
невероятно расширились. Мы знаем, что все тела состоят из молекул, молекулы состоят из
атомов, атомы состоят из электронов и ядер, ядра состоят из протонов и нейтронов,
протоны и нейтроны состоят из… Впрочем, на этом пока можно остановится, мы и так
уже вернулись к электрону, но не к «кусочку» янтаря, а к мельчайшей элементарной
частице, способной взаимодействовать с некоторыми другими частицами также как
«кусочки янтаря, потертые шерстью».
8. 1 Два вида электрических зарядов.
Если некоторые частицы (или тела) обладают способностью принимать участие в
электрических
взаимодействиях, то имеет смысл приписать им некоторую
характеристику, которая и будет указывать на это их свойство. Такая характеристика
получила название электрический заряд. Тела, принимающие участие в электрических
взаимодействиях называются заряженными. Таким образом, термин «электрически
заряженный» является синонимом выражения «участвует в электрических
взаимодействиях». Почему некоторые элементарные частицы обладают электрическим
зарядом, а другие нет – никому не известно!
Дальнейшие рассуждения, основанные на экспериментальных данных, призваны
конкретизировать эту характеристику, по возможности, сделать ее количественной.
История изучения электрических явлений длительна и полна драматизма, …
Далее мы опишем ряд простых опытов, которые можно провести дома «на кухне», или в школьной
лаборатории. При их объяснении мы будем пользоваться теми знаниями, которые получены в течение
многими учеными нескольких сотен лет, в результате многочисленных и разнообразных экспериментов.
Сейчас, мы воспроизведем в очень упрощенной форме некоторые этапы экспериментальных исследований,
выводы из которых послужили основой современной теории электрических взаимодействий.
Для проведения экспериментов, прежде всего, следует научиться получать
заряженные тела. Простейший метод достижения этой цели – электризация трением.
Например, хорошо электризуется, (то есть приобретает электрический заряд) стекло, если
его потереть шелком. Появление электрического заряда проявляется в том, что такая
палочка начинает притягивать кусочки бумаги, волоски, пылинки и т.д.
Также можно установить, что многие другие вещества также электризуются
посредством трения. Зная результат
заранее, в качестве второго «источника»
электричества выберем эбонитовую палочку, потертую шерстью. Назовем электрический
заряд, который появляется на стекле – «стеклянным», а заряд на эбоните «смоляным2».
Далее нам необходим «прибор», который мог бы реагировать на присутствие
электрического заряда. Для этого подвесим на нити легкий стаканчик, скрученный из
кусочка фольги. Легко проверить, что этот стаканчик не заряжен - чтобы мы не
подносили к нему, карандаш, руку, учебник физики и т.д., никакого действия на стаканчик
не проявляется.
1
Напомним, что термин электричество происходит от греческого названия янтаря – «электрон».
Во-первых, эбонит это застывшая смола, а во-вторых, такие термины являются историческими, на заре
изучения электрических явлений именно так назывались различные типы электрических зарядов.
2
105
Поднесем к незаряженному стаканчику заряженную стеклянную электрическую
палочку (рис. 141). Стаканчик притягивается к ней, как и другие мелкие тела. По углу
отклонения нити (при известной массе стаканчика и длине
нити) можно даже рассчитать силу притяжения. Если стаканчик
не соприкоснулся с заряженной палочкой он остается
незаряженным, что легко можно проверить экспериментально.
Если же стаканчик прикоснется к заряженной палочке, то он
резко оттолкнется от нее. Если теперь убрать палочку,
стаканчик окажется заряженным, что можно проверить, если
поднести к нему другое незаряженное тело. Например, он будет
притягиваться к поднесенной руке.
Аналогичные результаты получаются, если заменить
стеклянную палочку, потертую о шелк, эбонитовой палочкой,
потертой о шерсть.
Таким образом, в этих экспериментах различие между
«стеклянным» и «смоляным» электричеством не проявляется.
Не будем пока, обсуждать, почему незаряженный стаканчик притягивается к
заряженной палочке, а заряженный стаканчик притягивается к незаряженной руке.
Единственный вывод, который мы сделаем из проведенного эксперимента – в результате
контакта стаканчик приобрел электрический заряд. Следовательно, электрический заряд
может передаваться от одного тела к другому.
Возьмем два одинаковых стаканчика из
фольги, подвесим рядом их на нитях одинаковой
длины. Если стаканчики зарядить одинаково (либо
с помощью стеклянной, либо с помощью
эбонитовой палочки), то стаканчики отталкиваются
(рис, 142). Если же стаканчики заряжены
различными зарядами, то они притягиваются.
Таким образом, мы доказываем, что
существует, по меньшей мере, два вида электрических зарядов.
Для дальнейших экспериментов заменим «измерительные стаканчики» более
совершенным прибором, который называется
электрометр (рис, 143). Прибор состоит из
металлического
стержня
и
легкой
металлической
стрелки,
которая
может
вращаться вокруг горизонтальной оси. Это
устройство помещено в металлический корпус,
закрытый стеклянными крышками. Угол
отклонения стрелки можно измерять с помощью
шкалы. Стержень со стрелкой закреплен в
корпусе с помощью плексигласовой втулки.
Стержень со стрелкой играют ту же роль, что и
стаканчики из фольги в предыдущих опытах –
при прикосновении
заряженного тела к
стержню, заряд будет перетекать на стержень и
на стрелку, что приведет к ее отклонению.
Причем, направление отклонения стрелки не зависит от вида сообщенного заряда.
Для дальнейших экспериментов будем использовать два одинаковых электроскопа.
Зарядим один из них с помощью, например, стеклянной палочки. Далее начнем соединять
стержни электрометров с помощью различных материалов. При соединении стержней с
помощью деревянной, незаряженных стеклянной, эбонитовой, пластмассовых палочек;
текстильных нитей, никаких изменений не происходит – один электрометр остается
106
заряженным, второй незаряженным.
Если же соединить стержни с помощью
3
металлической проволоки, то оказываются заряженными оба электрометра. Причем,
отклонение
стрелки
первоначально
заряженного
электрометра уменьшится (рис. 144).
Из результатов этого опыта можно сделать два
важных вывода: во-первых, некоторые материалы (металлы)
могут передавать электрический заряд, другие (стекло,
пластмасса, дерево) нет; во-вторых, заряд может изменяться,
быть больше или меньше. Эти же эксперименты можно
повторить с использованием и второго вида («смоляного»)
электричества. Результаты окажутся такими же –
материалы, которые проводят «стеклянное» электричество,
проводят и «смоляное». Если «стеклянный» заряд
перераспределяется между электрометрами, то также себя
ведет и «смоляной» заряд.
Итак, мы можем разделить материалы на две группы – те,
которые передают электрический заряд (эти материалы
назвали проводники), и те, которые не передают
электрический заряд (их назвали изоляторы). Кстати, стержень электрометра отделен от
корпуса с помощью втулки из изолятора, чтобы электрический заряд не «растекался» по
корпусу, а оставался на стержне и стрелке.
Различные отклонения стрелки электрометра однозначно свидетельствуют о том,
что сила взаимодействия между заряженными телами может быть различной, поэтому и
величины зарядов могут быть различными. Следовательно, заряд можно характеризовать
некоторой численной величиной (а не так, как мы говорили ранее – «есть, или нет»).
Еще один интересный результат – если к стержню заряженного электрометра прикоснуться рукой,
то электрометр разряжается – заряд исчезает. Даже на основании этих качественных наблюдений можно
объяснить, куда исчезает заряд, при прикосновении руки. Человеческое тело является проводником,
поэтому заряд может перетечь в тело человека.
Для подтверждения этой идеи о количественном характере заряда можно провести
следующий опыт. Зарядим один электрометр – заметим угол отклонения стрелки.
Соединим его со вторым электрометром – угол отклонения стрелки заметно уменьшится.
Уберем контакт между приборами и рукой разрядим второй электрометр, после чего
опять соединим электрометры – отклонение стрелки опять уменьшится. Таким образом,
электрический заряд можно делить на части. Можно
провести и обратный эксперимент – постепенно добавляя
заряд электрометру.
«Смешаем» сейчас, два
имеющихся
вида
электричества. Для этого зарядим один электрометр
«стеклянным» электричеством, а второй – «смоляным»,
стараясь, чтобы начальные отклонения стрелок обоих
электрометров были примерно одинаковыми. После этого
соединим
стержни
электрометров
металлической
проволокой (на изолирующей ручке, чтобы заряды не
убежали»). Результат этого опыта может вызвать
удивление – оба электроскопа разрядились, или
«стеклянное»
и
«смоляное»
электричество
нейтрализовали,
скомпенсировали
друг
друга.
Следовательно, оказывается возможным приписать
различным видам заряда различные алгебраические знаки
3
При проведении этого к металлической проволоке нельзя прикасаться голыми руками – иначе электроскоп
сразу разряжается. Поэтому лучше использовать металлический стержень на деревянной или пластмассовой
ручке.
107
– один заряд назвать положительным, второй отрицательным. Разумно предположить, что
сила взаимодействия зависит от суммарного заряда. Если первоначально электрометры
были заряжены разными видами электричества, но в разной степени (отклонения стрелок
– различны), а потом их соединить, то произойдет лишь частичная компенсация зарядов –
стрелки будут отклонены, но в гораздо меньшей степени.
Исторически сложилось, что положительным назвали «стеклянный» заряд, а
«смоляной» заряд стал отрицательным4.
Описанный нами прибор, электрометр, позволяет лишь качественно судить о величине зарядов,
проводить с ним количественные измерения невозможно. Попробуйте, например, поднести к заряженному
электрометру руку (не прикасаясь к стержню) – отклонение стрелки увеличится! Поднесите к
незаряженному стержню заряженную палочку, не прикасаясь к стержню – стрелка отклонится, хотя
электрометр не заряжен. К объяснению этих фактов мы вернемся позднее.
8.2 Закон Кулона.
Для количественного изучения электрических зарядов и электрических
взаимодействий потребуются более точные измерительные приборы.
Такие измерения были впервые проведены французским физиком Шарлем
Кулоном в 1785 году. Чтобы исключить влияние размеров и формы взаимодействующих
тел на силу электрического взаимодействия, Ш. Кулон исследовал взаимодействие малых
шариков, размеры которых значительно меньше расстоянии между ними. Как мы знаем,
для описания таких тел используется модель материальной точки, только в данном случае
материальная точка наделяется еще одной характеристикой - электрическим зарядом q .
Такую модель - заряженную материальную точку называют точечным зарядом. Часто
точечное заряженное тело называют кратко - заряд.
Кроме того, закон взаимодействия заряженных тел имеет наиболее простой вид для
неподвижных тел. Раздел физики, изучающий взаимодействие неподвижных заряженных
тел называется электростатикой, а силы взаимодействия электростатическими.
Ш. Кулон
сконструировал и создал специальный прибор, позволивший
экспериментально открыть основной закон взаимодействия
заряженных тел. Схема прибора Ш. Кулона показана на рисунке 146.
На очень тонкой серебряной нити подвешен тонкий легкий
непроводящий стержень (играющий также роль стрелки), на одном
конце которого закреплен
маленькие шарик, а на другом
противовес. Верхний конец нити закреплен на вращающейся головке
прибора, угол поворота которой можно точно отсчитывать. Внутри
прибора имеется еще один шарик такого же размера, укрепленный на
изолирующей подставке. Все эти части помещены в стеклянный
цилиндрический сосуд, чтобы предохранить шарики от движения
воздуха. Это прибор получил название крутильные весы. Обратите внимание, что
принципиально крутильные весы Кулона не отличаются от наших «стаканчиков» из
фольги, подвешенных на нитях.
Первоначально, Ш. Кулон очень тщательно измерил зависимость угла
закручивания серебряной нити от приложенного к ней момента сил. Зная длину стрелки и
измеряя угол закручивания нити, можно с высокой точностью измерять силу,
действующую на шарик, расположенный на стержне. В результате проведенных опытов,
Ш. Кулон установил, что при неизменных зарядах на шариках сила взаимодействия
между ними обратно пропорциональна квадрату расстояния между центрами шариков
1
F∝ 2.
r
4
«Смоляное» электричество ничем не хуже «стеклянного», выбор знака – чистая условность. К слову, один
из полюсов магнита мы до сих пор называем «северным», а второй «южным» - то есть обходимся без
положительного и отрицательного магнетизма.
108
Более сложная задача – исследовать зависимость силы взаимодействия от
величины зарядов шариков, тем более, что единицы измерения заряда во время
проведения этих экспериментов еще не существовало. Ш. Кулон применил оригинальную
идею. Сначала оба шарика заряжаются, при этом стрелка весов поворачивается на
некоторый угол. Используя вращающуюся головку на конце нити можно установить
шарики на известном определенном расстоянии. После этого к одному шарику (проще
неподвижному) надо прикоснуться точно таким же шариком. Так как шарики одинаковы,
то разумно предположить, что заряд равномерно распределится между ними. Таким
способом можно уменьшить заряд шарика ровно в два раза. При уменьшении заряда угол
закручивания нити уменьшится. С помощью вращающейся головки стрелку можно
вернуть в исходное положение. По измеренному новому значению угла закручивания
нити можно определить, как изменилась сила взаимодействия, при неизменном
расстоянии между телами. Процедуру деления заряда как одного, так и второго шарика
можно продолжить. В результате проведенных измерений Ш. Кулон пришел к выводу,
что сила взаимодействия прямо пропорциональна зарядам шариков. Аналогичные
результату были получены, если заряды шариков противоположны, только в этом случае
отталкивание сменялось притяжением.
В результате проведенных опытов Ш. Кулон сформулировал закон взаимодействия,
который носит его имя:
Два неподвижных точечных заряда в вакууме взаимодействуют с силой
пропорциональной произведению зарядов, обратно пропорциональной квадрату
расстояния между ними и направленной вдоль прямой, соединяющей эти тела.
Дадим несколько комментариев к приведенной формулировке:
- приведенный закон справедлив для точечных тел, размеры которых значительно меньше
расстояния между ними;
- если заряженные тела находятся в некоторой среде, то сила электрического
взаимодействия изменяется, поэтому указание о вакууме является обязательны;
- сила является векторной величиной, поэтому в законе, определяющем силу, обязательно
упоминание о направлении действия силы; как установлено Ш. Кулоном
электростатические силы являются центральными.
Сила электростатического взаимодействия может быть записана в виде
qq
F = k 1 22 ,
(1)
r
где q1 , q 2 - заряды тел, r - расстояние между ними, k неопределенный пока коэффициент пропорциональности.
Этот же закон в векторной форме имеет вид
r
qq r
F21 = k 1r 2 r12 ,
(2)
r
r
здесь F21 - сила, действующая на второе тело со стороны
r
первого, r12 - вектор, проведенный от первого тела ко второму
(рис. 147).
В векторной формулировке автоматически учтено направление действующей силы
– если знаки зарядов одинаковы, то заряды отталкиваются, если знаки зарядов различны,
r
r
то тела притягиваются (вектор F21 направлен противоположно вектору r12 ). Отметим
r
r
также, что электростатические силы удовлетворяют третьему закону Ньютона F21 = − F12 .
Как видите, математическая формулировка закона электростатических
взаимодействий Ш. Кулона практически полностью совпадает с законом всемирного
тяготения И. Ньютона. Возможно, такое совпадение не является случайным, а связано со
свойствами трехмерного пространства, в котором мы живем. Единственное отличие в этих
законах заключается в том, что гравитационное взаимодействие всегда проявляется как
109
притяжение тел, а электрически заряженные тела могут как притягиваться, так и
отталкиваться.
Прежде чем переходить к обсуждению следствий и приложений закона Кулона нам
необходимо обсудить свойства электрического заряда и установить единицы его
измерения.
8.3 Единицы измерения электрического заряда.
Сейчас нам проще всего установить величину единицы заряда на основании закона
Кулона. Для этого можно положить коэффициент пропорциональности в формулах (1)-(2)
равным единице и дать следующее определение единицы заряда: два единичных заряда,
находящихся на единичном расстоянии, взаимодействуют с единичной силой. Кстати
именно так определяется величина заряда в одной из систем единиц измерения СГСЭ,
которой до сих пор с удовольствием пользуются некоторые физики-теоретики.
В
общепринятой (и обязательной) системе единиц СИ принято другое определение
единицы заряда, основанное на другом физическом законе – законе взаимодействия
электрических токов Ампера, строгое определение этой единицы мы дадим при изучении
взаимодействия токов. Основная причина такого определения заключается в том, что
создать эталон силы тока технически намного проще, чем эталон электрического заряда.
Поэтому в системе СИ в качестве основной электрической единицы выбрана единица
силы тока – Ампер. Единица заряда в этой системе является производной. Эта единица
носит название Кулон (сокращенно Кл), в честь автора основного закона электростатики.
По определению 1 Кулон это заряд, который протекает через поперечное сечение
проводника при силе тока в 1 Ампер за 1 секунду: [Кл ] = [А] ⋅ [с ] .
Можно обратится к аналогии с законом всемирного тяготения - как мы упоминали,
на основании этого закона можно было бы установить единицы гравитационной массы.
Однако оказалось удобней установить эталон инерционной массы – килограмм. Поэтому в
законе всемирного тяготения появился размерный коэффициент пропорциональности гравитационная постоянная.
Аналогично, так как единица заряда установлена на основании закона Ампера, в
законе Кулона коэффициент пропорциональности должен иметь размерность, а его
численное значение определяется экспериментально.
Для упрощения многих формул электростатики коэффициент пропорциональности
в системе СИ записывают в несколько непривычной форме
1
k=
,
(1)
4πε 0
где константа ε 0 называется электрической постоянной. Поэтому формула закона Ш.
Кулона в системе СИ имеет вид
1 q1 q 2
F=
,
(2)
4πε 0 r 2
Экспериментально5 определенное численное значение электрической постоянной равно
Кл 2
−12
ε 0 ≈ 8,85 ⋅ 10
. При расчетах удобно использовать значение константы
Н ⋅ м2
1
Н ⋅ м2
k=
≈ 9 ⋅ 10 9
.
4πε 0
Кл 2
5
В 1985 году были переопределены основные единицы системы СИ. В частности в качестве точной
фундаментальной точной константы принята скорость света в вакууме. В связи с этим электрическая
постоянная стала точной константой, так как она связана со скоростью света.
110
Физический смысл коэффициента k очевиден – два заряда величиной в 1 Кл
каждый, находящиеся на расстоянии в 1 метр взаимодействуют с силой 9 ⋅ 10 9 Н .
Обратите внимание громадность этой силы! Для электростатики заряд в 1 Кулон является
очень большим – описанные нами стеклянные и эбонитовые палочки при электризации
трением имеют заряды порядка 10 −10 Кл .
8.4 Закон сохранения электрического заряда.
Использованный Ш. Кулоном способ деления заряда неявно предполагает, что при
соприкосновении двух одинаковых шариков их суммарный заряд сохраняется.
Фактически Ш. Кулон использовал гипотезу о сохранении электрического заряда.
Многочисленные эксперименты по измерению зарядов в различных системах
подтвердили эту гипотезу. В настоящее время считается точно установленным закон
сохранения электрического заряда: суммарный электрический заряд замкнутой
системы сохраняется.
Так при электризации если одно тело приобретает положительный заряд, то какоето другое обязательно заряжается отрицательно. Так при взаимодействии стекла и шелка
стекло заряжается положительно, а шелк отрицательно. При соединении проводников
электрический заряд перераспределяется между проводниками, но их суммарный заряд
остается неизменным.
Свойство сохранения электрического заряда объясняется в рамках современных
представлений о строении вещества. Все вещества построены из электрически
заряженных частиц, важнейшими из которых являются отрицательно заряженные
электроны и положительно заряженные протоны. Заряды электрона т протона по модулю
равны. В обычном, незаряженном состоянии, суммарный заряд протонов полностью
компенсируется зарядом электронов, или число электронов равно числу протонов.
Поэтому для таких тел закон сохранения электрического заряда есть закон сохранения
электрически заряженных частиц. Более подвижными частицами являются электроны,
поэтому в большинстве случаев при электризации происходит переход части электронов с
одного тела на другое. Тело, имеющее избыток электронов заряжено отрицательно, тело с
недостатком электронов заряжено положительно.
Однако закон сохранения электрического заряда имеет и более фундаментальный
смысл. Элементарные частицы при взаимодействиях могут «превращаться» друг в друга
– может происходить рождение одних частиц и исчезновения других. Во всех этих
превращениях суммарный электрический заряд сохраняется – если появляется
положительно заряженная частица, то обязательно появляется отрицательно заряженная
частица. В чем причина такого поведения частиц неизвестно. Единственный ответ,
который можно дать на этот вопрос – «Так устроен наш мир!»
8.5 Дискретность электрического заряда. Объемная плотность заряда.
Чрезвычайно точные измерения показали, что заряд протона по модулю в точности
равен заряду электрона. Более того, другие заряженные элементарные частицы также
имеют электрические заряд в точности равный заряду электрона. Таким образом, заряд
электрона является минимально возможным электрическим зарядом, минимальной
«порцией» электрического заряда, поэтому его называют элементарным зарядом.
Многочисленные попытки, продолжающиеся и в настоящее время, обнаружить частицы,
имеющие заряд, меньший элементарного, закончились неудачей. Так как заряды тел
обусловлены избытком или недостатком электронов, то их заряд оказывается кратным
элементарному заряду.
Первые измерения величины заряда электрона провел в 1909 – 1913 году
американский физик Р. Милликен. Идея его экспериментов очень проста – он наблюдал
движение микроскопических капелек масла в электрическом поле. Ему удалось показать,
что заряды капелек кратны элементарному заряду, и измерить величину этого заряда. В
111
настоящее время заряд электрона измерен с очень высокой точностью, относительная
погрешность измерений меньше чем 10 −8 . По современным данным величина этого
заряда равна e ≈ 1,60 ⋅ 10 −19 Кл . Малость этой величины объясняет, почему в течение
длительного времени дискретность6 электрического заряда не наблюдалась.
Первые теории электричества строились на представлении о заряде, как некоторой особой
электрической жидкости (о молекулярной структуре настоящих жидкостей тогда тоже не было известно).
Долгие споры велись о том, сколько электрических жидкостей существует, одна или две. Отголоски этих
жидкостных представлений дошли до нас в многочисленных терминах – заряд перетекает (отсюда
электрический ток), конденсатор обладает электрической емкостью (показывающий сколько электрической
жидкости он может вместить), и др. Электрон, а следовательно и элементарный заряд, был открыт только в
1897 году английским физиком Дж. Дж. Томсоном.
Дискретность электрического заряда проявляется только в том случае, когда
заряды тел малы, сравнимы с элементарным зарядом. Не случайно Р. Милликен в своих
экспериментах использовал микроскопические капельки, заряды которых составляли
несколько элементарных зарядов. Во многих случаях нет необходимости учитывать
дискретность электрического заряда. То есть в математическом описании перейти к
непрерывному описанию распределения зарядов. В этом случае можно ввести понятие
объемной плотности заряда как функции координат ρ ( x, y, z ) , как отношение величины
заряда ∆q , содержащегося в малом объеме ∆V вокруг точки с координатами (x, y, z ) , к
величине этого объема
∆q
ρ ( x, y , z ) =
, при ∆V → 0 .
∆V
Это определение полностью совпадает с обсуждавшимся ранее понятием плотности «в
точке».
8.6 Инвариантность электрического заряда.
Одним из основных принципов всей физики является принцип относительности –
во всех инерциальных системах отсчета все физические явления протекают одинаково.
Или, что равносильно, равномерное движение не влияет на протекание физических
процессов. Поэтому, при введении любой физической величины важным является вопрос
о зависимости этой величины от скорости движения тела, или от выбора системы отсчета.
Экспериментальный данные свидетельствуют, что электрический заряд обладает
инвариантностью, то есть его величина не зависит от выбора системы отсчета, не
зависит от скорости движения частиц.
Не случайно в данной нами формулировке закона Ш. Кулона опоминается о неподвижности
заряженных тел. При движении зарядов между ними действуют также и магнитные силы. Проблемы,
связанные с взаимодействием движущихся частиц, мы будем обсуждать позднее, при изучении магнетизма.
8.7 Принцип суперпозиции для электростатических сил.
Вернемся к обсуждению закона Ш. Кулона. При этом
мы постоянно будем использовать его аналогию с законом
всемирного тяготения – раз формулировки совпадают, то и
следствия из них должны совпадать. Поэтому у нас есть
возможность достаточно быстро повторить основные выводы.
Прежде всего, обратим внимание, что сила
взаимодействия точечных тел прямо пропорциональна
величине заряда. Это обстоятельство является математическим
выражением принципа суперпозиции: сила, действующая
на точечный заряд
q0 со стороны системы зарядов
q1 , q 2 ,...q k ... равна сумме сил, действующих со стороны
6
Дискретность означает «прерывность, раздельность», существование только в виде отдельных порций.
112
каждого из зарядов q1 , q 2 ,...q k ... (рис. 148)
r
r r
r
F( рез.) = F1 + F2 + ...Fk + ...
(1)
Подчеркнем, что формула закона Ш. Кулона выражает справедливость принципа
суперпозиции, который является обобщением экспериментальных фактов.
Принцип суперпозиции выражает независимость сил электростатических
взаимодействий, взаимодействие с одним зарядом, никак не влияет на взаимодействие с
остальными.
Закон Ш. Кулона для точечных тел и принцип
суперпозиции позволяют, в принципе, вычислять силы
взаимодействия между заряженными телами конечных размеров.
Для этого необходимо мысленно разбить каждое из тел на малые
участки, каждый из которых можно рассматривать как точечный
заряд (Рис. 149), затем вычислить двойную сумму сил
взаимодействия между всеми парами точек.
Для использования этого метода расчета силы
взаимодействия, необходимо знать распределение зарядов внутри каждого из
взаимодействующих тел. В отличие от гравитационного взаимодействия, во многих
случая (точнее, практически всегда) распределение зарядов на телах заранее не известно.
Так одно заряженное тело существенно влияет на распределение зарядов на другом,
поэтому расчет сил взаимодействия между заряженными телами является еще более
сложной задачей, чем расчет силы гравитационного взаимодействия. Для подтверждения
этого утверждения сошлемся на существование сил притяжения между заряженным и
незаряженным телом.
Так сила электростатического взаимодействия между точечными зарядами обратно
пропорциональна квадрату расстояния между телами, то сила взаимодействия между
равномерно заряженными сферами равна силе взаимодействия между точечными
зарядами, равными зарядам сфер, и расположенными в центрах этих сфер. Аналогичный
вывод справедлив и для любых сферически симметричных распределений зарядов.
Иными словами – сферически симметричные заряды можно собрать в одну точку – в
центр, при этом силы электростатического взаимодействия не изменятся. И. Ньютон
доказал это утверждения для гравитационных сил, совсем скоро мы докажем его для
электростатических взаимодействий.
Одинаковая зависимость гравитационных и электростатических сил от расстояния
позволяет сравнивать эти силы между собой. Для двух одинаковых точечных тел
имеющих массы m и заряды q , отношение электрической к гравитационной силе
выражается формулой
⎛ 1 e2 ⎞
⎜
⋅ ⎟
Fэл. ⎜⎝ 4πε 0 r 2 ⎟⎠
e2
=
.
=
⎛ m 2 ⎞ 4πε 0 Gm 2
Fгр.
⎜⎜ G ⋅ 2 ⎟⎟
r ⎠
⎝
Так для двух протонов это отношение приблизительно равно 1⋅ 10 36 , а для более легких
электронов даже
4 ⋅ 10 42 - весьма внушительные числа! Поэтому при описании
взаимодействия заряженных частиц гравитационным взаимодействием пренебрегают. В
наших экспериментах (со стаканчиками), гравитационные взаимодействия между ними
также пренебрежимо малы, по сравнению с электрическими. Практически во всех
случаях, где появляются электрические силы, гравитационные уходят на второй план.
Громадность электрических сил, во многом, обуславливает их широкое применение в
нашей жизни, и необходимость их изучения.
113
§ 9. Электрическое поле и его свойства.
Громадные успехи механики, основанной на законах динамики И. Ньютона и
закона Всемирного тяготения, привели к тому, что в течение более ста лет (весь XVIII век)
в физике господствовала, так называемая, теория дальнодействия. В рамках этой теории
считалось возможным, что тела могут воздействовать друг на друга на расстоянии, без
всякого «посредника» передающего взаимодействия. Так, для того, чтобы лошадь тянула
телегу, необходима соответствующая упряжь, для передачи звука необходима среда, хотя
бы воздух. А гравитационные силы могут передаваться от одного тела к другому через
пустое пространство. Так закон всемирного тяготения дает выражение для силы
взаимодействия, но не объясняет механизма возникновения этой силы. Можно даже
сказать, что такой вопрос и не ставился учеными – достаточно вспомнить знаменитое
высказывание И. Ньютона: «Гипотез не измышляю». Еще одним важным аспектом
дальнодействия
является
бесконечная скорость передачи взаимодействий – так
изменение положения одного тела в тот же момент времени проявляется в изменении
силы его воздействия на другие тела, независимо от того, на каком расстоянии они
находятся.
Первые теории электричества и магнетизма так же строились на идее
дальнодействия. Основной закон электростатики Ш. Кулона совпадает с законом
всемирного тяготения, его идеология также аналогична: заряженные тела могут
взаимодействовать на расстоянии, изменение положения одного тела мгновенно влияет на
силы, действующие на другие тела, природа электрических взаимодействий не известна и
«не интересна», достаточно знать формулу для силы взаимодействия. Аналогично была
построена и теория магнитных взаимодействий. Даже используя эту ошибочную, как мы
теперь убеждены, концепцию дальнодействия, ученые (в основном французские Ш.
Кулон, С. Пуассон, П. Лаплас, А. Ампер, Ж. Био, Ф. Савар и др.) сумели построить
достаточно совершенную и математически изящную теорию электрических и магнитных
явлений, многие из положений которой сохраняют свое значение до настоящего времени.
«Французская» электродинамика начала XIX века добилась значительных успехов, не
смотря на ошибочность общего подхода, потому, что она рассматривала «статику»
электростатику и магнитостатику - поведение неподвижных (или движущихся с малыми
скоростями) заряженных тел. Действительно, в стационарном случае время
распространения взаимодействий не играет никакой роли – все тела либо неподвижны,
либо движутся со скоростями, значительно меньшими скорости распространения
взаимодействий. Поэтому модели с бесконечной скоростью распространения
взаимодействий вполне приемлемы, а вопрос о наличии или отсутствии «посредника»
имеет только общепознавательный интерес.
Ситуация радикально изменилась, когда физики приступили к
изучению
электродинамики, изучению электрических и магнитных явлений, изменяющихся во
времени. В этих описании этой группы явлений «статика» оказалась бессильна.
Принципиально новые идеи были высказаны в 20-х – 30-х годах XIX века выдающимся
английским ученым М. Фарадеем. Основная из них - понятие электрического и
магнитного полей, или единого электромагнитного поля. Подчеркнем,
не
математической абстракции, а объективно существующей реальности, особого вида
материи. Электромагнитное поле и является «посредником», переносчиком электрических
и магнитных взаимодействий. В рамках полевых воззрений электромагнитные
взаимодействия трактуются следующим образом: заряды создают электромагнитное
поле, которое воздействует на другие заряженные тела. Иными словами, произошло
возвращение к идее «близкодействия», взаимодействие возможно только при
непосредственном контакте, была найдена «веревочка», передающее взаимодействие от
одного заряженного тела к другому. Физические идеи М.Фарадея о поле развиты другим
английским физиком Дж. К. Максвеллом, которому удалось найти математические
уравнения, описывающие все свойства электромагнитных полей и их взаимодействий с
114
заряженными телами. Система уравнений Дж. К. Максвелла и в настоящее время является
основой электродинамики. Почти не преувеличивая, можно сказать, что теоретическая
электродинамика это уравнения Дж. К. Максвелла и их решения. Фактически содержание
нашего дальнейшего курса – это изучение этой системы уравнений.
В течение достаточно длительного промежутка времени (всего XIX века) считалось, что
электрические и магнитные явления (в том числе и оптические!) есть процессы (натяжения, сгущения,
колебания, волны) в особой среде эфире, который заполняет все пространство. Эту особую среду наделяли
рядом механических свойств, пытаясь свести электромагнитные явления к механическим, дать им
механическое истолкование. Электромагнитное поле также рассматривалось как поле особых напряжений
эфира. С помощью теории удалось «объяснить» и описать множество явлений, даже предсказать новые, до
того неизвестные явления. Однако по мере накопления опытных данных свойства эфира «становились» все
более сложными и экзотическими, наконец, этот эфир никак не удавалось обнаружить экспериментально.
Наконец, в начале XX века эфир оказался изгнанным из физики, так же как флогистон, теплород и
электрические жидкости.
Каковы же подтверждения объективного существования электромагнитного поля?
Как мы уже подчеркивали, электромагнитные явления в статических системах с
неподвижными (или медленно движущимися) зарядами могут быть достаточно точно
описаны и без привлечения понятия поля. Существование полей проявляется только в
системах, быстроизменяющихся со временем. В таких системах существенным и
наблюдаемых является запаздывание взаимодействий – изменение системы в одной точке
проявляется в других точках через некоторый промежуток времени, необходимый для
распространения возмущения от одной точки до другой. Дж. К. Максвеллу удалось
вычислить (!) скорость распространения электромагнитных взаимодействий, она
оказалась равной скорости света. Этот открытие позволило выдвинуть гипотезу об
электромагнитной природе света.
Еще одним подтверждением объективного существования электромагнитного поля
является М. Фарадеем в 1831 году явление электромагнитной индукции. Суть этого
явления заключается в возникновении электрического поля (легко регистрируемого) при
изменении магнитного поля. То есть, на заряженное тело может подействовать
электрическая сила, даже если нет других электрических зарядов – сила со стороны поля.
Противоположное явление – порождение магнитного поля изменяющимся электрическим
полем было теоретически предсказано Дж. К. Максвеллом. В последствии это
предсказание было подтверждено экспериментально.
Так как электрические и магнитные поля могут порождать друг друга,
электромагнитное поле может существовать в виде волн. Существование
электромагнитных волн также было предсказано Дж. К. Максвеллом, экспериментально
эти волны были открыты1 и исследованы немецким физиком Г. Герцем. Начиная свои
эксперименты, Г.Герц ставил целью опровергнуть теорию Дж. К. Максвелла. Однако, по
его же словам, чем больше он ставил экспериментов, тем больше убеждался в ее
справедливости. Электромагнитное поле в виде волн может оторваться от зарядов, то есть
существовать (и регистрироваться) без зарядов, его породивших, «как свет угасших
звезд». Не является ли это окончательным доказательством того, что электромагнитное
поле материальная реальность!
Упомянутые явления указывают, что реально существует единое электромагнитное
поле. Однако в некоторых простых случаях оказывается возможным разделить
электрические и магнитные поля, рассматривать их независимо. Так в системе
неподвижных электрических зарядов электромагнитное поле проявляется как
электрическое (электростатическое), в системе постоянных электрических токов – как
магнитное (магнитостатическое). Условность такого разделения легко показать. Пусть в
некоторой системе отсчета все заряды неподвижны – создаваемое ими поле является
электростатическим. Если описывать эти же заряды в другой «движущейся системе
1
Нельзя сказать, что электромагнитные волны не были известны – ведь свет это тоже электромагнитная
волна, но до Дж. К. Максвелла никто не знал этого.
115
отсчета, то заряды будут движущимися, следовательно, они будут создавать и магнитное
поле.
Так как электромагнитное поле является объективной реальностью, то для его
изучения необходимо ввести, определить, набор его характеристик, параметров. Среди
них есть, как новые для нас, с которыми предстоит познакомиться, так и наши «старые
знакомые» - энергия, импульс и т.д.
Не смотря на то, что существование полей проявляется наиболее ярко только при
их изменение, изучение характеристик и свойств электромагнитного поля мы начинаем с
изучения поля, создаваемого неподвижными электрическими зарядами, такое поле
называется электростатическим.
Современная теория электромагнитного поля базируется на концепции близкодействия. Эта общая
идея не могла не оказать влияния на теорию гравитации. В 1916 году знаменитый немецкий физик А.
Эйнштейн выдвинул новую теорию гравитации – общую теорию относительности. Эта теория также
основана на идее близкодействия, в этой теории описывается гравитационное поле, гравитационные волны и
др. Не смотря на ряд существенных экспериментальных подтверждений справедливости новой теории, до
настоящего времени она представляет скорее теоретический интерес. При описании движений планет,
спутников, космических кораблей используется ньютоновская теория, так скорости движения этих тел
значительно меньше скорости света, поэтому модель мгновенной скорости распространения
гравитационного взаимодействия оказывается приемлемой.
Для описания поведения микрочастиц,
движущихся со скоростями, близкими к скорости света, гравитационные силы слишком слабы, поэтому ими
пренебрегают.
9.1 Напряженность электрического поля.
В рамках представлений о поле взаимодействие зарядов, описываемое законом Ш.
Кулона, «разбивается» на две части – один заряд создает электрическое поле, которое
воздействует на другой заряд. Таким образом, электрический заряд играет двойную роль:
с одной стороны он является источником поля, а с другой индикатором, прибором для
изучения поля.
Основное свойство электростатического поля заключается в его воздействии на
неподвижные электрические заряды. Поэтому характеристика электрического поля
должна быть связана с силой, действующей на заряженное тело. Чтобы определить
характеристику поля в каждой пространственной точке,
в качестве «прибора»,
регистрирующего поле, необходимо использовать очень малое тело, размерами которого
можно пренебречь. Моделью такого тела является электрически заряженная материальная
точка, то есть точечный заряд. Так как этот точечный заряд используется в качестве
датчика, мы будем также его называть пробный заряд. Итак, для изучения поля в
r
некоторой точке, в эту точку следует поместить пробный заряд q и измерить силу F ,
действующую на него. Согласно закону Ш. Кулона величина этой силы пропорциональна
величине пробного заряда. Следовательно, отношение этой силы к величине заряда не
зависит от величины заряда, поэтому данное это отношение является характеристикой
r
поля, которая называется напряженностью электрического поля - E .
Напряженностью электрического поля называется отношение силы,
действующей на точечный заряд, помещенный в данную точку поля, к величине
этого заряда
r
r F
(1)
E= .
q
Можно дать и эквивалентную формулировку: напряженность электрического поля есть
сила, действующая на единичный положительный заряд, помещенный в данную
точку поля.
Так как сила является векторной физической величиной, то и напряженность
электрического поля также является векторной величиной. Пробный заряд можно
поместить в любую пространственную точку, поэтому и вектор напряженности также
определен в любой точке пространства. Таким образом, для описания электрического
116
поля нам необходимо использовать следующую математическую конструкцию: каждой
точке пространства (задаваемой тремя координатами (x, y, z ) ), ставится в соответствие
r
вектор E (имеющий три компоненты (E x , E y , E z )). Иными словами, нам необходимо
задать три функции, каждая из которых зависит от трех координат. С подомной
математической конструкцией мы познакомились при описании движения жидкости – это
векторное поле2. Поэтому при описании электрического поля мы можем использовать
образы и методы, с которыми мы познакомились при изучении течения жидкости.
9.2 Напряженность электрического поля точечного заряда.
Рассмотрим электрическое поле, создаваемое одним
точечным зарядом. Чтобы подчеркнуть, что этот заряд мы
рассматриваем как источник поля, обозначим его величину
прописной буквой Q (Рис. 150). Возьмем произвольную
пространственную точку A . Для определения напряженности
электрического поля, поместим в эту точку пробный заряд q .
Согласно закону Ш. Кулона, сила, действующая на пробный
заряд равна
r
1 Qq r
⋅
F=
r,
4πε 0 rr 3
r
где r - вектор, проведенный от заряда источника Q , к точке A , в которой рассчитывается
поле (точку наблюдения). Тогда, по определению,
напряженность поля в этой точке равна
r
r F
1
Q r
E= =
⋅ r3 r ,
(1)
q 4πε 0 r
и, заметьте, не зависит от величины пробного заряда. Формула (1), определяет
напряженность электрического поля, создаваемого точечным зарядом.
Фактически
формула
(2)
определяет
вектор
напряженности в зависимости от 6 координат: трех
координат заряда и трех координат точки наблюдения.
Введем декартовую систему координат (Рис. 151), пусть
в этой положение заряда определяется радиус-вектором
r
r1 (или координатами (x1 , y1 , z1 ) ), а положение точки
r
наблюдения - радиус-вектором r0 (или координатами
(x0 , y 0 , z 0 ) ). Тогда вектор rr , соединяющий заряд и
точку наблюдения, фигурирующий в формуле (1), равен
r r r
r = r0 − r1 . Следовательно, напряженность поля в точке
наблюдения определяется формулой
r r
r
Q (r0 − r1 )
(2)
⋅ r r3,
E=
4πε 0 r0 − r1
r r r
Перепишем эту формулу в координатной форме. Длина вектора r = r0 − r1 равна
r r
r r
2
2
2
r0 − r1 = ( x0 − x1 ) + ( y 0 − y1 ) + ( z 0 − z1 ) , а его проекция на ось X - (r0 − r1 ) x = x0 − x1 .
Следовательно, проекция вектора напряженности на ось X определяется по формуле
(x0 − x1 )
Q
⋅
.
(3)
Ex =
4πε 0 ( x − x )2 + ( y − y )2 + ( z − z )2 3 2
(
0
1
0
1
0
1
)
2
Сказываются недостатки языка – математическое векторное поле описывает физическое электрическое
поле. Думаем, что проблемы различения этих понятий будут возникать не слишком часто.
117
Две аналогичных формулы надо выписать и для оставшихся компонент вектора напряженности.
Оцените очередной раз прелесть векторной записи (2) – во-первых, короче; во-вторых, не зависит от
выбора системы координат, хотя конкретные численные расчеты, все равно необходимо проводить в
координатной форме.
9.3 Принцип суперпозиции для напряженности электрического поля.
Для расчета поля, создаваемого нескольким
точечными зарядами, следует воспользоваться
принципом суперпозиции. Пусть электростатическое
поле создается системой зарядов (Рис, 152)
Q1 , Q2 ...Qk ,...(k = 1,2...N ) , расположенных в точках,
положение которых задается радиус-векторами
r r r
r1 , r2 ...rk ... Для определения напряженности в
r
некоторой точке с радиус-вектором r0 , поместим в
нее пробный заряд q . По принципу суперпозиции для
электростатических сил, результирующая сила,
действующая на пробный заряд равна сумме сил,
действующих со стороны каждого заряда в отдельности
r r
r r
r r
r r
N
r
Qk q (r0 − rk )
Qk q (r0 − rk )
Q1 q (r0 − r1 ) Q2 q (r0 − r2 )
F( рез.) =
⋅
+
⋅
+ ...
⋅
+ ... =
⋅ r r 3.
4πε 0 rr0 − rr1 3 4πε 0 rr0 − rr2 3
4πε 0 rr0 − rrk 3
4
πε
r0 − rk
0
k =1
Для вычисления напряженности поля, эту силы необходимо разделить на величину
пробного заряда. Тем самым, мы доказали принцип суперпозиции для напряженности
электрического поля: напряженность поля, создаваемого системой зарядов, равна
сумме напряженностей полей, создаваемых каждым зарядом в отдельности:
r r
N
r r
r
r
r
Qk (r0 − rk )
E = E1 + E 2 + ...E k + ... =
Ek =
⋅ r r 3.
(1)
4
πε
r
−
r
0
k
k =1
0
k
∑
∑
∑
Если заряды распределены внутри некоторого тела непрерывно (заданы объемной
плотностью зарядов), то для вычисления напряженности поля необходимо разбить тело на
малые части, каждую из которых можно рассматривать как точечный заряд, после чего
можно воспользоваться формулой (1).
Таким образом, закон Ш. Кулона и принцип суперпозиции позволяет рассчитать
напряженность поля, создаваемого произвольной (но известной) системы зарядов. Правда,
провести такие расчеты не легко, но это уже проблемы математики, а не физики.
9. 4 Силовые линии электростатического поля.
Для наглядного графического представления поля удобно
использовать силовые линии – направленные линии, касательные
к которым в каждой точке совпадают с направлением вектора
напряженности электрического поля (Рис. 153). Согласно,
определению силовые линии электрического поля обладают
рядом общих свойств (сравните со свойствами линий тока
жидкости):
1. Силовые линии не пересекаются (в противном случае, в точке пересечения можно
построить две касательных, то есть в одной точке, напряженность поля имеет два
значения, что абсурдно).
2. Силовые линии не имеют изломов (в точке излома опять можно построить две
касательных).
3. Силовые линии электростатического поля начинаются и заканчиваются на зарядах.
Так напряженность поля определена в каждой пространственной точке, то силовую
линию можно провести через любую пространственную точку. Поэтому число силовых
118
линий бесконечно велико. Число линий, которые используются для изображения поля,
чаще всего определяется художественным вкусом физика-художника. В некоторых
учебных пособиях рекомендуется строить картину силовых линий так, чтобы их густота
была больше там, где напряженность поля больше. Это требование не является строгим, и
не всегда выполнимым, поэтому силовые линии рисуют, удовлетворяя
сформулированным свойствам 1-3.
Очень просто построить силовые линии поля создаваемого
точечным зарядом. В этом случае силовые линии представляют
собой набор прямых, выходящих (для положительного), или
входящих (для отрицательных) в точку расположения заряда
(Рис..154). Такие семейства силовых линий полей точечных
зарядов демонстрируют, что заряды являются источниками поля,
по аналогии с источниками и стоками поля скоростей жидкости.
Доказательство того, что силовые линии не могут начинаться или заканчиваться в тех
точках, где заряды отсутствуют, мы проведем позднее.
Картину силовых линий реальных полей можно воспроизвести экспериментально.
В невысокий сосуд следует влить небольшой слой касторового масла и всыпать в него
небольшую порцию манной крупы. Если масло с крупой поместить в электростатическое
поле, то крупинки манной крупы (они имеют слега вытянутую форму) поворачиваются по
направлению напряженности электрического поля и выстраиваются приблизительно
вдоль силовых линий, по прошествии нескольких десятков секунд в чашке
вырисовывается картина силовых линий электрического поля. Некоторые такие
«картинки» представлены на фотографиях.
Также можно провести теоретический расчет и построение силовых линий. Правда,
эти расчеты требуют громадного числа вычислений, поэтому реально (и без особого
труда) проводятся с использованием компьютера, чаще всего такие построения
выполняются в некоторой плоскости.
При разработке алгоритмов расчета картины силовых линий встречается ряд проблем, требующих
своего разрешения. Первая такая проблема - расчет вектора поля. В случае электростатических полей,
создаваемых заданным распределением зарядов, эта проблема решается с помощью закона Кулона и
принципа суперпозиции. Вторая проблема - метод построения отдельной линии. Идея простейшего
алгоритма, решающего данную задачу, достаточна очевидна. На малом участке каждая линия практически
совпадает со своей касательной, поэтому следует построить множество отрезков касательных к силовым
линиям, то есть отрезков малой длины l , направление которых
совпадает с направлением поля в данной точке. Для этого необходимо,
прежде всего, рассчитать компоненты вектора напряженности в
заданной точке E x , E y и модуль этого вектора E =
E x2 + E y2 .
Затем можно построить отрезок малой длины, направление которого
совпадает с направлением вектора напряженности поля. его проекции
на оси координат вычисляются по формулам, которые следуют из рис.
155: ∆x = l
E
Ex
;∆y = l y . Затем следует повторить процедуру,
E
E
начиная с конца построенного отрезка. Конечно, при реализации
такого алгоритма встречаются и другие проблемы, носящие скорее
технический характер.
На рисунках 156 показаны силовые линии полей создаваемых двумя точечными
зарядами. Знаки зарядов указаны, на рисунках а) и б) заряды по модулю одинаковы, на
рис. в), г) различны - какой из них больше предлагаем определить самостоятельно.
Направления силовых линий в каждом случае также определите самостоятельно.
Интересно, отметить, что М.Фарадей рассматривал силовые линии электрического поля как
реальные упругие трубки, связывающие между собой электрические заряды, такие представления очень
помогали ему предсказывать и объяснять многие физические явления.
Согласитесь, что прав был великий М. Фарадей – если мысленно заменить линии упругими
резиновыми жгутами, характер взаимодействия очень нагляден.
119
9. 5 Поток вектора напряженности электрического поля. Теорема Гаусса.
Как и для любого векторного поля важно рассмотреть свойства потока
электрического поля. Поток электрического поля определяется традиционно.
Выделим малую площадку площадью ∆S , ориентация которой задается
r
единичным вектором нормали n (Рис, 157). В пределах малой площадки
электрическое поле можно считать однородным3, тогда поток вектора
напряженности ∆Φ E определяется как произведение площади площадки
на нормальную составляющую вектора напряженности
r r
∆Φ E = E cos α∆S = E ⋅ n ∆S = E n ∆S .
(1)
r r
r
r
где E ⋅ n = E cos α - скалярное произведение векторов E и n ; E n нормальная к площадке компонента вектора напряженности.
В произвольном электростатическом поле поток
вектора напряженности через произвольную поверхность,
определяется следующим образом (Рис. 158):
- поверхность разбивается на малые площадки ∆S (которые
можно считать плоскими);
r
- определяется вектор напряженности E на этой площадке
(который в пределах площадки можно считать постоянным);
- вычисляется сумма потоков через все площадки, на которые
разбита поверхность
(
)
(
)
3
Электрическое поле называется однородным, если во всех точках вектор напряженности постоянен, как по
величине, так и по направлению – обычное определение однородности, как для любого поля.
120
Φ = ∆Φ 1 + ∆Φ 2 + ∆Φ 3 + ... =
∑ ∆Φ = ∑ E cosα ⋅ ∆S .
i
i
i
i
i
(1)
i
Эта сумма называется потоком вектора напряженности электрического поля через
заданную поверхность. Трудно найти явный физический смысл этой величины, но как
мы указывали, поток векторного поля является полезной вспомогательной
математической величиной.
Рассмотрим электрическое поле точечного заряда Q (рис.
159). Это поле обладает сферической симметрией – модуль вектора
напряженности зависит только от расстояния для заряда, в любой
точке вектор напряженности направлен радиально, вдоль прямой,,
соединяющей заряд с точкой наблюдения. Окружим заряд сферой,
произвольного радиуса R , центр которой совпадает с точечным
зарядом. Во всех точках поверхности сферы вектор напряженности
электрического поля направлен вдоль нормали к поверхности
сферы (поэтому угол между ними равен нулю), его модуль
постоянен и по закону Ш. Кулона равен
Q
E=
.
4πε 0 R 2
Выделим на поверхности сферы малую площадку площадью ∆S i , поток вектора
напряженности через эту площадку равен
Q
∆Φ i =
∆S i .
4πε 0 R 2
Так как модуль вектора напряженности во всех точках сферы одинаков, суммирование
потоков через поверхность сферы, сводится к суммированию площадей участков, на
которые разбивается сфера. Вычислим поток вектора напряженности
Q
Q
Q
Q
ΦE =
∆S i =
∆S i =
⋅ 4πR 2 =
,
(2)
2
2
2
ε0
4πε 0 R
4πε 0 R i
4πε 0 R
i
∑
здесь
∑ ∆S
i
∑
=4πR 2 - площадь поверхности сферы. Обратите внимание, что этот поток не
i
зависит от радиуса сферы. Итак, поток вектора напряженности электрического поля
точечного заряда через поверхность сферы равен отношению заряда к электрической
постоянной.
Для обобщения полученного результата, вспомним теоремы о потоке несжимаемой
жидкости. Самое важное – распределение скоростей от точечного источника, описывается
такой же зависимостью, как и напряженность электрического поля, созданного точечным
источником. Следовательно, и потоки этих векторных полей подчиняются одинаковым
законам. Поэтому, мы не будем подробно доказывать каждое утверждение, только
приведем его основные этапы.
1. Выражение для суммарного потока (3) вывод можно обобщить для
любой замкнутой поверхности, окружающей точечный заряд.
Поток вектора напряженности электрического поля точечного заряда
через любую замкнутую поверхность, окружающую заряд, равен величине
Q
заряда, деленного на электрическую постоянную: Φ E =
(Рис. 160)
ε0
2. Пусть внутри поверхности находится несколько зарядов (Рис. 161).
Так как для вектора напряженности электрического поля
электрического поля справедлив принцип суперпозиции, то такой же
принцип будет справедлив и для потока вектора напряженности.
Следовательно, поток вектора напряженности электрического поля,
121
созданного системой зарядов Q1 , Q2 ,... , через любую замкнутую поверхность,
окружающую заряды, равен сумме зарядов, деленную на электрическую постоянную ε 0 :
ΦE =
Q1
ε0
+
Q2
ε0
+ ...
3. Если заряд Q ′ находится вне замкнутой поверхности (Рис. 162),
то поток вектора напряженности поля, созданного этим зарядом
через эту поверхность равен нулю: Φ E = 0 .
Наконец, можно объединить эти положения и
сформулировать
теорему
о
потоке
вектора
напряженности электрического поля (Рис. 163):
Поток вектора напряженности электрического поля
через любую замкнутую поверхность равен сумме
зарядов, находящихся внутри этой поверхности,
деленную на электрическую постоянную ε 0 :
ΦE =
Q1 + Q2 + ..
ε0
.
Эта важнейшая теорема впервые сформулирована немецким математиком К.
Гауссом и носит его имя (теорема Гаусса).
В отличие от напряженности поля, которая является точечной характеристикой
поля (определена в каждой точке поля), поток этого вектора есть характеристика
некоторого объема (усредненной, интегральной) характеристикой. Если в некоторой части
пространства электрическое поле отсутствует (напряженность равна нулю), то и поток
вектора напряженности через любую поверхность, находящуюся в этой части также равен
нулю. Обратное утверждение не верно – если поток вектора напряженности равен нулю,
то из этого не следует, что поле отсутствует. Единственный вывод, который можно
сделать из равенства потока нулю – внутри рассматриваемой поверхности суммарный
заряд равен нулю.
Заряды, находящиеся вне рассматриваемой замкнутой поверхности, создают
электрическое поле, в том числе и внутри объема, ограниченного рассматриваемой
поверхностью. Только суммарный поток поля созданного этими зарядами равен нулю
(«сколько втекает – столько вытекает»). Можно сказать, что заряды вне поверхности,
перераспределяют поток поля, создаваемый зарядами внутри поверхности (Рис. 164).
Теорема Гаусса строго доказывается на основании закона Ш. Кулона, поэтому она
не несет нового физического содержания. Из теоремы Гаусса, легко выводится формула
закона Ш. Кулона. Поэтому с точки зрения физики, теорема Гаусса и закон Кулона
122
эквиваленты, это один и тот же физический закон, облаченный в разные математические
оболочки.
9.6 Поле равномерно заряженной плоскости.
Решим задачу, которая нам неоднократно понадобится в дальнейшем. Пусть
электрическое поле создается зарядами, которые равномерно распределены по
бесконечной плоскости.
Конечно, в реальности бесконечно больших
поверхностей не существует. В данном случае, мы
подразумеваем, что точка A , в которой рассчитывается
напряженность поля, находится на расстоянии h от
плоскости, которое значительно меньше расстояний до
краев заряженного участка (Рис. 165). В этом случае
влияние зарядов, расположенных достаточно далеко от рассматриваемой точки
становится пренебрежимо малым. Проводить расчеты для бесконечно больших
плоскостей оказывается проще, чем для конечных участков.
В качестве характеристики распределения зарядов введем величину σ поверхностную плотность заряда. Выберем на плоскости произвольную точку с
координатами ( x, y ) , окружим ее малой площадкой площадью ∆S . Пусть заряд этой
выделенной площадки равен ∆Q , тогда средняя поверхностная плотность заряда
∆Q
определяется как отношение заряда площадки к ее площади σ =
. При уменьшении
∆S
площади выделенной площадки, получим поверхностную плотность заряда в данной
точке поверхности
∆Q
σ ( x, y ) =
, при ∆S → 0 .
(1)
∆S
Для равномерно заряженной поверхности поверхностная плотность заряда постоянна
σ ( x, y ) = σ = const .
Для
расчета
напряженности
поля
воспользуемся законом Ш. Кулона и принципом
суперпозиции.
Разобьем заряженную плоскость на малые
участки. Такое разбиение можно проводить
различными способами. Расчеты упрощаются, если
мысленно разбить плоскость на тонкие кольца, а
затем каждое кольцо разделить на малые участки
(Рис. 166). Каждый малый участок плоскости можно
рассматривать как точечный заряд величиной
∆Q = σ∆S ,
который
создает
поле,
вектор
r
∆E
направлен вдоль прямой,
напряженности которого
соединяющий заряд с точкой наблюдения A (Рис. 167). Полная
напряженность электрического поля будет равна векторной сумме
напряженностей полей, создаваемых отдельными участками
плоскости. Ясно, что результирующий вектор напряженности будет
направлен перпендикулярно плоскости (обозначим это направление
осью z ). Действительно, для каждого заряда ∆Q найдется
симметрично расположенный заряд ∆Q' , сумма векторов
r
r
напряженностей полей ∆E + ∆E ' , создаваемых этими зарядами,
будет направлена вдоль оси z .
123
Вычислим напряженность поля, создаваемого равномерно заряженным кольцом, в
точке находящейся на оси кольца на расстоянии h от его центра.
Разобьем кольцо на малые участки, заряд каждого из них обозначим ∆Qi . В точке
r
наблюдения вектор напряженность поля ∆E i , создаваемого этим зарядом, направлен
вдоль линии, соединяющей заряд и точку наблюдения. Величина этого вектора может
быть рассчитана по закону Ш. Кулона
∆Qi
∆E i =
,
4πε 0 r 2
где r = h 2 + R 2 - расстояние от заряда то точки наблюдения.
Как мы показали, результирующий вектор напряженности направлен вдоль оси кольца.
r
Поэтому для его расчета достаточно просуммировать проекции векторов ∆E на эту ось
h
∆EiZ = ∆Ei cos α = ∆Ei . Просуммируем проекции векторов напряженностей полей,
r
создаваемых всеми зарядами, на которые мы разбили кольцо
∆Qi
E Z = ∆E1Z + ∆E 2 Z + ... =
∆EiZ =
⋅ cos α .
4πε 0 r 2
i
i
∑
∑
Так как все заряды находятся на равных расстояниях r от точки наблюдения, а векторы
r
∆E i образуют равные углы α с осью Z , вычисление этой суммы сводится суммированию
зарядов (постоянные множители можно вынести за знак суммы):
∆Qi
Q
Q
h
cos α
EZ =
∆Qi =
⋅
.
(2)
cos α =
cos α =
2
2
2
4πε 0 (h 2 + R 2 )3 2
4πε 0 r
4πε 0 r i
4πε 0 r
i
∑
∑
Заметим, что в центре кольца напряженность поля равна нулю, затем с ростом h
напряженность поля возрастает до некоторого максимального значения, после чего
начинает монотонно убывать. Причем на больших
расстояниях при h >> R в формуле (2) можно
пренебречь R в знаменателе, при этом напряженность
Q
поля определяется формулой E Z ≈
, которая
4πε 0 h 2
соответствует напряженности поля точечного заряда.
Данный результат понятен, на расстояниях значительно
превышающих радиус кольца, кольцо можно
рассматривать как точечный заряд. График функции (2)
показан на рисунке 168.
Далее для вычисления напряженности поля,
созданного всей плоскостью, необходимо просуммировать
выражения (2) по всем кольцам, на которые была разбита
плоскость. Такое суммирование, в принципе, можно
провести, но этот расчет требует привлечения операции
интегрирования, поэтому заниматься этим не будем. Тем
более, что результат можно получит гораздо быстрее,
использую теорему Гаусса.
Для использования этой теоремы для определения
напряженности поля, необходимо рассмотреть симметрию
поля, которая, очевидно связана с симметрией зарядов.
Распределение зарядов не изменится, если плоскость
r
сместить на любой вектор a , лежащий в самой плоскости.
Поэтому при таком смещении не изменится и напряженность поля (рис. 169).
Следовательно, напряженность поля может зависеть только от расстояния до плоскости
124
h . Любая прямая, перпендикулярная плоскости является осью симметрии, то есть при
повороте плоскости на любой угол относительно любой оси, перпендикулярной
плоскости, распределение зарядов не изменяется – следовательно, и вектор
напряженности при таком повороте не изменится, поэтому этот вектор должен быть
перпендикулярен плоскости. Наконец, заряженная плоскость является плоскостью
симметрии для поля. Поэтому в симметричных точках векторы напряженности также
симметричны. Выявленные свойства симметрии электрического поля позволяют выбрать
поверхность, для которой можно выразить поток вектора напряженности в простой
форме. Итак, в качестве такой поверхности выберем поверхность прямого цилиндра,
образующие которого перпендикулярны плоскости, а основания площадью S
параллельны ей и находятся на равных расстояниях от плоскости.
Прежде всего, заметим, что поток вектора напряженности через боковую
поверхность цилиндра равен нулю, так как во всех точках боковой поверхности векторы
r
r
напряженности E и нормали n взаимно перпендикулярны (поэтому cos α = 0 ) (рис. 170).
Поток через верхнее основание цилиндра может быть
записан в виде Φ = ES , так модуль напряженности
поля на основании цилиндра постоянен, а по
направлению совпадает с вектором нормали. Такое же
значение имеет поток через нижнее основание. Таким
образом, суммарный поток вектора напряженности
электрического поля через поверхность цилиндра
равен Φ E = 2 ES . По теореме Гаусса этот поток равен
заряду внутри поверхности Q = σS , деленному на
σS
электрическую постоянную Φ E = 2 ES =
. Их этого
ε0
равенства выражаем модуль вектора напряженности
электрического поля
E=
σ
.
2ε 0
(4)
Как видите, с использованием теоремы Гаусса нам удалось решить поставленную
задачу «в одно действие». Главная составляющая успеха – анализ симметрии поля,
позволивший разумно выбрать поверхность, для использования теоремы Гаусса. Также
обратите внимание, что напряженность данного поля одинакова во всех точках,
следовательно, это поля является однородным. Подчеркнем, независимость
напряженности поля от расстояния до плоскости h никак не следует из симметрии поля,
это результат нашего расчета.
9.7 Поле равномерно заряженной сферы.
Рассмотрим теперь с помощью теоремы Гаусса, поле, создаваемое равномерно
заряженной тонкой сферической оболочки. Опять начнем с рассмотрения симметрии
поля. Очевидно, что поле, также как распределение зарядов имеет сферическую
симметрию. Это означает, что модуль вектора напряженности зависит только от
расстояния до центра сферы (или во всех точках, находящихся от центра сферы на одном
расстоянии, модуль напряженности постоянен), а направление –
радиальное, от центра сферы к точке наблюдения.
Выберем в качестве замкнутой поверхности, к которой
применим теорему Гаусса, сферу, концентрическую с заряженной
оболочкой (Рис. 171). Пусть радиус сферы r больше радиуса
оболочки. Тогда во всех точках этой сферы вектор напряженности
направлен вдоль нормали к поверхности, а его модуль постоянен.
Поэтому поток вектора напряженности через сферу равен
125
произведению модуля напряженности на площадь сферы Φ E = E ⋅ 4πr 2 . По теореме
Q
Гаусса это поток равен заряду сферы, деленному на электрическую постоянную Φ E =
.
ε0
Из равенства этих выражений получаем зависимость напряженности поля от расстояния
Q
E=
.
(1)
4πε 0 r 2
Полученная формула, соответствует формуле закона Кулона для точечного заряда,
следовательно, вне сферы, поле равномерно заряженной сферы, совпадает с полем
точечного заряда, помещенного в центре сферы. Таким образом, результат, на
доказательство которого И. Ньютон затратил несколько лет, получен нами почти
автоматически. Подчеркнем, что для доказательства формулы (1) помимо теоремы К.
Гаусса, потребовалось рассмотреть симметрию поля.
Поле внутри заряженной сферической оболочки также должно
обладать
сферической
симметрией.
Поэтому,
поток
вектора
напряженности электрического поля через сферу, концентрическую с
заряженной оболочкой и расположенную внутри нее (Рис. 172) также
выражается формулой Φ E = E ⋅ 4πr 2 . Однако внутри этой сферы
электрических зарядов нет, поэтому, из теоремы К. Гаусса следует, что
напряженность поля внутри сферы равна нулю. Подчеркнем, если бы
теорема Гаусса была не справедлива, то внутри равномерно заряженной оболочки
существовало бы электрическое поле.
Таким образом, функция, описывающая напряженность
поля равномерно заряженной сферы радиуса R , имеет вид
(график этой функции показан на рисунке 173)
⎧0, при r < R
⎪
.
E (r ) = ⎨ Q
⎪ 4πε r 2 , при r > R
0
⎩
126
9.8 Потенциальность электростатического поля. Потенциальная энергия
взаимодействия электрического заряда с электрическим полем.
Если электрическое тело действует на электрически заряженные тела, то оно
способно совершить работу по перемещению заряженных тел.
Электростатическое поле, создаваемое точечным зарядом, является центральным,
то есть сила, действующая на точечный заряд в таком поле, направлена вдоль прямой,
соединяющей заряд-источник и пробный заряд. Ранее мы показали, что любая
центральная сила является потенциальной, то есть работа этой силы не зависит от формы
траектории, а определяется только начальным и конечным положением тела.
Вкратце напомним доказательство этого важнейшего
утверждения. Пусть точечный пробный заряд q движется в
центральном поле, создаваемом неподвижным зарядом Q (Рис.
174). Сила, действующая на пробный заряд, определяется
законом Кулона
r
1 Qq r
F=
⋅
r,
4πε 0 rr 3
r
где r - вектор, проведенный от заряда источника Q , к точке A ,
в которой находится пробный заряд. При движении заряда по
дугам окружностей с центром на заряде Q (например, по дугам
AB, CD ) работа электрической силы равна нулю, так векторы силы и перемещения
взаимно перпендикулярны. При движении же в радиальном направлении (например, по
отрезкам BC, DE ) работа зависит только от начального и конечного расстояния до заряда
источника. Так работы электростатического поля при перемещении по отрезкам DE и
D1 E1 , очевидно равны. Самое красивое доказательство этого утверждения связано с
симметрией поля – повернем нашу систему вокруг оси проходящей через источник, так,
что бы отрезок D1 E1 совпал с отрезком DE - распределение поля при этом не изменится,
почему должна изменится работа поля?
Так как для напряженности электростатического поля справедлив принцип
суперпозиции, то потенциальным является любое электростатическое поле.
Действительно, пусть точечный заряд q находится в электрическом поле, создаваемым
системой неподвижных точечных зарядов Q1 , Q2 ,...Qk ...(k = 1,2,..N ) . При перемещении
r
заряда на малый вектор перемещения ∆r , по определению, электрическое поле совершит
r
r
работу δA = Fрез. ⋅ ∆r , где
r
r r
r
F рез. = F1 + F2 + ... + Fk + ... =
N
r
∑F
k
k =1
результирующая сила, действующая на движущийся заряд q , равная сумме сил,
действующих со стороны каждого из неподвижных точечных зарядов Qk . Работа этой
силы может быть вычислена по формуле
N
r
r
r
r r
r r
r
r
r
δA = F рез. ⋅ ∆r = F1 ⋅ ∆r + F2 ⋅ ∆r + ... + Fk ⋅ ∆r + ... =
Fk ⋅ ∆r .
(1)
∑
k =1
Для того, чтобы вычислить работу по конечному
участку
траектории,
необходимо
разбить
траекторию на малые участки (Рис. 175), затем с
помощью формулы (1) вычислить работу на
каждом малом участке, после чего их
просуммировать
127
r
r r
r r
r
A = δA1 + δA2 + δA3 + ... = F1( рез.) ⋅ ∆r1 + F2( рез.) ⋅ ∆r2 + F3( рез.) ⋅ ∆r3 + ...
(2)
Фактически, данная сумма является двойной, так как каждая результирующая сила,
является суммой сил, в соответствии с формулой (1). Обратим внимание, что в формуле
(2) результирующая сила изменяется, так как вычисляется в разных точках траектории.
Как мы показали ранее, работа электрического поля точечного заряда не зависит от
формы траектории, то есть каждое слагаемое из формулы (1) не зависит от формы
траектории, следовательно, и вся сумма не зависит от формы траектории. Таким образом,
любое электростатическое поле является потенциальным.
Следовательно, для точечного заряда, находящегося в электростатическом поле можно
U ( x, y, z ) . Эта функция имеет
ввести потенциальную энергию взаимодействия
следующий физический смысл: работа электрического поля при перемещения
точечного заряда из одной точки с координатами (x1 , y1 , z1 ) в другую, с координатами
(x 2 , y 2 , z 2 ) равна изменению потенциальной энергии, взятому с противоположным
знаком:
A = − ∆U = −(U ( x 2 , y 2 , z 2 ) − U ( x1 , y1 , z1 )) .
(3)
Изменение знака в данном определении достаточно логично: если электрическое поле
совершило положительную работу ( A > 0 ) , то его энергия уменьшается (∆U < 0 ) .
Для
вычисления
работы
силы
взаимодействия
между двумя точечными
заряженными телами достаточно подсчитать эту
работу при движении вдоль радиального отрезка
при изменении расстояния от r1 до r2 (Рис. 176).
Если
построить
зависимость
силы
1 Qq
взаимодействия между зарядами F =
от расстояния r между телами, тогда
4πε 0 r 2
площадь под графиком этой зависимости в указанных
пределах и будет равна искомой работе (Рис. 177).
Зависимость силы электростатического взаимодействия от
расстояния
аналогична
силе
гравитационного
взаимодействия, с одним существенным отличием:
гравитационная сила всегда есть сила притяжения, а
электрическая может быть как силой притяжения, так и
силой отталкивания. В частности два положительных заряда
отталкиваются.
Поэтому
выражение
для
работы
электрического поля, будет аналогично формуле для работы
гравитационной силы, но иметь противоположный знак
Qq ⎛ 1 1 ⎞
⎜ − ⎟.
A12 =
4πε 0 ⎜⎝ r1 r2 ⎟⎠
Эта работа равна уменьшению потенциальной энергии взаимодействия, то есть
Qq ⎛ 1 1 ⎞
⎜ − ⎟ = −∆U = −(U 2 − U 1 ) .
A12 =
4πε 0 ⎜⎝ r1 r2 ⎟⎠
Из этого выражения можно определить выражение для потенциальной энергии
электростатического взаимодействия двух точечных зарядов
1 Qq
U (r ) =
.
(4)
4πε 0 r
При таком определении потенциальная энергия взаимодействия двух зарядов
одного знака положительна и стремится к нулю при бесконечном расстоянии между
телами U (∞ ) = 0 . Сила взаимодействия зарядов противоположных знаков направлена в
128
противоположную сторону, поэтому работа этой силы при увеличении расстояния между
зарядами будет отрицательна. Однако нам нет необходимости делать какие-то
дополнительные оговорки, так как формула (4) автоматически учитывает знаки зарядов –
если заряды противоположны, то их произведение (соответственно и энергия)
отрицательны.
Знак потенциальной энергии взаимодействия зарядов имеет очень наглядный смысл. Заряды одного
знака отталкиваются, поэтому при их «разбегании» на бесконечно большое расстояние, электрическое поле
совершит положительную работу – следовательно, изначально система этих зарядов обладает способностью
совершить работу, поэтому ее энергия положительна, при удалении зарядов друг от друга их энергия
уменьшается до нуля. Заряды противоположных знаков притягиваются, для того чтобы удалить их на
бесконечно большое расстояние, внешние силы должны совершать положительную работу. При этом
энергия пары зарядов должна возрастать, следовательно, изначально она отрицательна, а при удалении
зарядов друг от друга возрастает до нуля. В целом обычная ситуация – притяжению соответствует
отрицательная энергия, а отталкиванию - положительная. Отметим только, что такая очевидность
справедлива только при выборе нулевого уровня потенциальной энергии на бесконечности.
Формула (4) определяет потенциальную энергию взаимодействия двух точечных
заряженных тел. Величины зарядов тел Q и q входят, как и следовало ожидать, в эту
формулу симметрично. Подразделение зарядов на заряд-источник и пробный заряд
является условным, их вполне можно поменять местами. Поэтому данную формулу
предпочтительнее записывать в симметричном виде: энергия взаимодействия двух
точечных зарядов q1 и q 2 равна
1 q1 q 2
,
(5)
U (r ) =
4πε 0 r
и имеет смысл работы, совершаемой полем при увеличении расстояния между зарядами
от r до бесконечности, независимо от того, движется ли первый заряд, или второй, или
движутся оба заряда, наконец, не зависимо от траекторий движения обоих зарядов.
Далее, нельзя сказать какому именно заряду «принадлежит» эта энергия, в дальнейшем
мы покажем, что энергия взаимодействия зарядов есть часть энергии самого
электростатического поля, то есть она «размазана» по всему пространству, где существует
поле, создаваемое этими зарядами.
Если система состоит из более чем двух зарядов, то для
подсчета энергии взаимодействия этих зарядов необходимо
просуммировать энергии взаимодействия всех пар зарядов
U = U 12 + U 13 + U 14 + ...
+ U 23 + U 24 + ...
+ U 34 + ... =
(6)
∑
qi q k
4πε 0 rik
по парам
1
здесь U ik - энергия взаимодействия зарядов qi и q k , находящихся на
расстоянии rik друг от друга (Рис. 178).
С несколько иной формой записи энергии взаимодействия зарядов мы
познакомимся чуть позднее.
9.9 Потенциал электростатического поля.
Введенная функция U ( x, y, z ) (потенциальная энергия взаимодействия точного
заряда и электрического поля), естественно, зависит от свойств поля и от величины
пробного заряда. Сила, действующая на заряженное тело, пропорциональна заряду,
следовательно, работа и потенциальная энергия взаимодействия также пропорциональны
величине пробного заряда. Поэтому если работу, по перемещению заряженного тела,
разделить на величину пробного заряда, то получим характеристику поля (не зависящую
от пробного заряда). Аналогично, если разделить потенциальную энергию взаимодействия
заряда с полем на величину заряда, то получим характеристику поля, которая называется
129
потенциалом электрического поля. Итак, потенциалом электрического поля ϕ ( x, y, z )
называется отношение потенциальной энергии взаимодействия электрического поля
и пробного точечного U ( x, y, z ) заряда к величине заряда:
U ( x, y , z )
ϕ ( x, y , z ) =
.
(1)
q
Потенциал электрического поля является размерной физической величиной, по
[U ] = Джоуль . В системе единиц СИ единица
определению размерность потенциала [ϕ ] =
[q ] Кулон
измерения потенциала называется Вольт (сокращенно В), и названа в честь итальянского
физика Алесандро Вольта. По определению
1 Джоуль
1 Дж
1 Вольт =
, 1В =
1 Кулон
1 Кл
или разность потенциалов между двумя точками равна 1 вольту, если при перемещении
заряда в 1 кулон электрическое поле совершает работу в 1 джоуль.
Задание для самостоятельной работы.
1. Выразите единиц разности потенциалов Вольт через основные единицы системы СИ.
Рассуждая о потенциальной энергии, мы неоднократно подчеркивали, что
физический смысл имеет только разность потенциальных энергий между точками, или
потенциальная энергия определяется с точностью до постоянного слагаемого, которое, в
свою очередь, зависит от выбора «нулевого» уровня энергии. Аналогичные рассуждения
полностью применимы и потенциальной энергии взаимодействия поля и заряда и
потенциалу электростатического поля. Таким образом, для однозначного определения
потенциала в любой точке пространства необходимо выбрать произвольную точку, в
которой потенциал принимается равным нулю. Так же как и в случае гравитационного
поля, в качестве точки нулевого потенциала выбирается «бесконечность», то есть точки
удаленные от зарядов на очень большое расстояние ϕ (∞ ) = 0 .
Особо подчеркнем, что такой выбор является произвольным, не обусловленным никакими
физическими законами. Более того, в некоторых случаях работа поля по перемещению заряда из данной
точки на бесконечно большое расстояние равна бесконечности, в таких случаях условие ϕ (∞ ) = 0
невозможно.
При выборе «нулевого» уровня на бесконечности
ϕ (∞ ) = 0 , потенциал
электростатического поля равен работе поля по перемещению единичного
A( x , y , z )→∞
положительного заряда из данной точки на бесконечность: ϕ ( x, y, z ) =
.
q
Разность потенциалов двух точек не зависит от выбора уровня нулевого
потенциала, поэтому именно эта величина имеет явный физический смысл и поддается
измерению. Работа, совершаемая силами электрического поля по перемещению
единичного положительного заряда равна разности потенциалов между этими
точками, взятой с противоположным знаком A1→2 = −(ϕ 2 − ϕ 1 ) . Данное высказывание
также можно рассматривать как определение разности потенциалов.
Введенная нами ранее напряженность электрического поля является точечной характеристикой
поля – она однозначно определяется свойствами поля в рассматриваемой точке. Не смотря на то, что мы
определили потенциал тоже в конкретной пространственной точке, потенциал является интегральной
характеристикой поля, так как зависит от свойств поля в области от рассматриваемой точки, до точки
нулевого потенциала.
Используя определение потенциала и выведенную формулу для потенциальной
энергии взаимодействия зарядов, легко получить выражение для потенциала
электростатического поля, создаваемого точечным зарядом Q
130
U (r )
1 Q
=
,
(2)
q
4πε 0 r
где r - расстояние от заряда источника Q до точки наблюдения с координатами (x, y, z ) , в
которой вычисляется потенциал поля. Так если заряд находится в точке с координатами
(x1 , y1 , z1 ) , а потенциал вычисляется в точке с координатами (x0 , y 0 , z 0 ) , расстояние между
ϕ ( x, y , z ) =
(x0 − x1 )2 + ( y 0 − y1 )2 + (z 0 − z1 )2
этими точками рассчитывается по формуле r =
.
Легко доказать, что для потенциала электростатического поля также справедлив
принцип суперпозиции: потенциал поля создаваемого системой зарядов
Q1 , Q2 ,...Qk ...(k = 1,2,..N ) равен сумме потенциалов, создаваемых каждым зарядом в
N
отдельности ϕ рез. = ϕ1 + ϕ 2 + ...ϕ k + ... =
∑ϕ
k
.
k =1
Таким образом, при известном распределении зарядов, задача вычисления потенциала в
произвольной точке становится чисто технической проблемой вычисления громоздких сумм. В некоторых
случаях такое суммирование проводится элементарно, в других требует привлечения интегрального
исчисления, а иногда и компьютерных расчетов. Однако, в любом случае – это проблема математическая;
физически задача решена: для потенциала справедлив принцип суперпозиции, а потенциал поля точечного
заряда определяется формулой (2).
Задание для самостоятельной работы.
1. Докажите принцип суперпозиции для потенциала электростатического поля.
9.10 Связь между потенциалом и напряженностью электрического поля.
Потенциал является важной характеристикой электрического поля, он определяет
всевозможные энергетические характеристики процессов, проходящих в электрическом
поле. Кроме того, расчет потенциала поля проще расчета напряженности, хотя бы потому,
что является скалярной (а не векторной) величиной. Безусловно, что потенциал и
напряженность поля связаны меду собой, сейчас мы установим эту связь.
Пусть в произвольном электростатическом поле точечный заряд q
r
совершил малое перемещение ∆r из точки 1 в точку 2 (Рис. 179).
r
Пренебрегая изменением напряженности поля E на этом участке,
работу, совершенную полем можно записать в виде
r r
r r
δA = F ⋅ ∆r = qE ⋅ ∆r .
По определению эта величина равна разности потенциалов, взятой с
противоположным знаком, деленной на величину заряда, поэтому
r r
δA
∆ϕ = −(ϕ 2 − ϕ1 ) = −
= − E ⋅ ∆r .
(1)
q
Если расстояние между точками 1 и 2 не
является малым, то необходимо эти точки
соединить произвольной линией (Рис. 180),
r r r
разбить ее на малые участки ∆r1 , ∆r2 , ∆r3 , и
просуммировать разности потенциалов между (1)
ними
r
r r
r r
r
ϕ1 − ϕ 2 = E1 ⋅ ∆r1 + E 2 ⋅ ∆r2 + E3 ⋅ ∆r3 + ...
(2)
Формула (2) позволяет рассчитать разность потенциалов между произвольными
точками, по известным значениям напряженности поля во всех точках.
131
Как и следовало ожидать, связь между разностью потенциалов
и напряженностью поля аналогична связи между изменением
потенциальной энергии и действующей силой. Так, если вдоль
некоторой прямой (назовем ее осью X ), проекция вектора
напряженности на эту ось изменяется по некоторому закону E X ( x ) ,
то площадь под графиком этой функции между точками с
координатами x1 и x 2 численно равна разности потенциалов между
этими точками, взятой с противоположным знаком.
Заметим, что если двигаться вдоль направления
вектора напряженности, то потенциал поля будет
уменьшаться, так как при таком движении поле совершает
положительную работу, поэтому энергия взаимодействия уменьшается.
Так как электростатическое поле является потенциальным, то результат
суммирования в формуле (2) не зависит от выбранной линии, важно только, чтобы она
начиналась в точке 1 и заканчивалась в точке 2. Кстати, с подобной конструкцией сумма
скалярных произведений вектора на малый элемент траектории мы уже неоднократно
встречались. Напомним, что такая сумма, вычисленная по замкнутой траектории,
называется циркуляцией векторного поля.
Так как электростатическое поле потенциально, то циркуляция
вектора напряженности электростатического поля по любой
замкнутой линии равна нулю ΓE = 0 (Рис. 182).
Таким образом, мы сформулировали вторую важнейшую теорему для вектора
напряженности стационарного электростатического поля. Никакого нового физического
содержания в этой теореме нет – это просто повторение в иной форме свойства потенциальности. Заметим
также, что теорема о циркуляции утверждает, что в электростатическом поле не может быть замкнутых
силовых линий, все силовые линии начинаются и заканчиваются на электрических зарядах, или что
равносильно – единственными источниками электростатического поля являются электрические заряды.
Заметим, что данной утверждении справедливо, только в статических полях (не зависящих от времени), в
дальнейшем мы познакомимся с электрическим полями, в которых существуют замкнутые силовые линии,
такие поля порождаются изменяющимися магнитными полями.
Задание для самостоятельной работы.
Докажите, что в электростатическом поле не могут существовать замкнутые
силовые линии.
Формула (1) позволяет выразить значение вектора напряженности через известное
распределение потенциала поля. Только не следует делить на вектор – такая операция в
математике еще не определена. Рассмотрим две близких точки 1 и
2, находящиеся на прямой, параллельной оси x на малом
расстоянии ∆x (Рис. 183). Пусть напряженность вблизи этих точек
r
равна E , и ее изменением пренебрежем из-за близости
рассматриваемых точек. Тогда разность потенциалов между этими
точками равна
r r
− ∆ϕ = ϕ 1 − ϕ 2 = E ⋅ ∆r = E x ∆x .
Из этого выражения законно находим проекцию вектора
напряженности на ось X :
∆ϕ
ϕ ( x + ∆x, y, z ) − ϕ ( x, y, z )
Ex = −
.
(3)
=−
∆x
∆x
Аналогично, рассматривая две близких точки 1 и 3, находящиеся на прямой, параллельной
оси Y на малом расстоянии ∆y , можно получить выражение для проекции вектора
напряженности на ось Y :
132
∆ϕ
ϕ ( x, y + ∆y, z ) − ϕ ( x, y, z )
=−
.
(4)
∆y
∆y
Выражение для проекции вектора на ось Z - E z также полностью аналогично
∆ϕ
ϕ ( x, y, z + ∆z ) − ϕ (x, y, z )
Ez = −
=−
.
(5)
∆z
∆z
Особо отметим, что величины ∆ϕ , фигурирующие в формулах (3)-(5) различны,
так как они выражают разности потенциалов между близкими точками, но смещенными в
различных направлениях.
Полученным выражениям для напряженности
поля можно дать и графическую интерпретацию (Рис.
184): коэффициент наклона касательной к графику
зависимости ϕ ( x ) , взятый с обратным знаком, численно
равен проекции вектора напряженности на ось x .
В общем случае потенциал электрического поля
зависит от трех координат точки, поэтому графически
представить эту зависимость невозможно. Мы уже
пользовались зависимостью потенциала от одной
координаты ϕ ( x ) и строили графики этой зависимости.
Фактически, мы задавали зависимость потенциала от одной координаты, при движении
вдоль прямой параллельной оси x , если мы выберем другую прямую, также
параллельную оси x , то получим другую функцию ϕ ( x ) . Поэтому при рассмотрении
подобных зависимостей надо явно указывать на какой прямой, рассматривается
потенциал. Проще всего, во избежание путаницы указывать в явном виде при каких
значениях других координат y 0 = const , z 0 = const рассматривается зависимость
ϕ ( x ) = ϕ ( x, y 0 , z 0 ) . Точно также можно изучать зависимость потенциала от двух
координат, считая третью постоянной: например, ϕ ( x, y ) = ϕ ( x, y, z 0 ) . То есть,
рассматривать распределение потенциала в некоторой плоскости параллельной
координатной плоскости xOy , находящей на расстоянии z 0 от нее. Графически эта
зависимость может быть представлена некоторой поверхностью, высота точек которой
пропорциональна потенциалу в данной точке, такую поверхность далее будем называть
потенциальной, по аналогии с потенциальными кривыми, рассмотренными нами ранее.
Так на рисунке в качестве примера показана потенциальная поверхность поля точечного
заряда, в плоскости, содержащей заряд этот заряд.
Если точечный заряд q находится в начале
некоторой системы координат, то потенциал поля,
создаваемого этим зарядом в произвольной точке с
координатами (x, y, z ) определяется формулой
q
q
.
(6)
ϕ ( x, y , z ) =
=
4πε 0 r 4πε 0 x 2 + y 2 + z 2
Ey = −
Если мы хотим построить распределение потенциала в
плоскости xOy , то в формуле (6) следует положить z = 0 .
Поверхность, описываемая этим уравнением, показана на
рисунке 185. Заметим, что в начале координат потенциал
стремится к бесконечности, поэтому изображение
потенциальной поверхности искусственно обрезан сверху.
Потенциальные поверхности строить не легко, для этого, как правило,
используется компьютер. Однако изображения таких поверхностей бывают очень
полезными при анализе движения заряженных частиц. Так движение положительно
133
заряженной частицы в поле, описываемом заданной потенциальной поверхностью,
аналогично движению массивного шарика в поле тяжести земли по геометрической
поверхности, которая совпадает с потенциальной.
На рисунке 186 для примера построены потенциальные поверхности поля,
создаваемого двумя одинаковыми по модулю зарядами: а) одинаковых знаков; б)
противоположных знаков.
Вторым способом графического представление потенциала является построение
эквипотенциальных поверхностей, то есть геометрического места точек, имеющих
одинаковый потенциал, то есть удовлетворяющих уравнению ϕ (x, y, z ) = ϕ 0 = const .
Так для поля точечного заряда (1) эквипотенциальными поверхностями являются
сферы, концентрические с точечным зарядом – все точки, находящиеся на одинаковом
расстоянии от заряда, имеют одинаковый потенциал. Формально, уравнение
эквипотенциальной сферы можно получить из функции (6). Из уравнения
q
= ϕ0
2
4πε 0 x + y 2 + z 2
2
⎛ q ⎞
⎟⎟ , причем сфера большего потенциала
следует уравнение сферы x + y + z = ⎜⎜
⎝ 4πε 0ϕ 0 ⎠
имеет меньший радиус.
2
2
2
Заметим, что симметрия эквипотенциальных поверхностей повторяет симметрию источников поля,
так поле точечного заряда сферически симметрично, то и
эквипотенциальные поверхности обязаны быть сферами.
Конечно, для увеличения наглядности, следует
рассматривать не одну эквипотенциальную поверхность, а
их семейство. Однако изобразить графически семейство
сложных поверхностей на одном рисунке крайне
затруднительно. Поэтому часто графически изображают
только
сечения
эквипотенциальных
поверхностей
некоторой плоскостью, или, что равносильно – множества
точек равного потенциала в некоторой плоскости (которые
являются линиями).
Линии равного потенциала и потенциальные
поверхности тесно связаны между собой. Фактически
линии
равного
потенциала
является
сечениями
потенциальной
поверхности.
Семейство
эквипотенциальных линий полностью аналогично линиям
равной высоты (изолиниям) на географической карте. На
134
рисунке 187 показана потенциальная поверхность электростатического поля, созданного
двумя точечными зарядами одного знака, но разной величины, в плоскости, содержащей
эти заряды. Ниже построено семейство эквипотенциальных линий этого поля в той же
плоскости. Эти линии являются линиями уровня для потенциальной поверхности.
В данном примере легко вообразить и семейство трехмерных эквипотенциальных
поверхностей. Система двух точечных зарядов обладает осевой симметрией – осью
симметрии является прямая, проходящая через оба заряда, на рисунке она обозначена как
ось X . Поэтому и поле, и его эквипотенциальные поверхности обладают осевой
симметрией – достаточно повернуть картину эквипотенциальных линий вокруг оси X ,
чтобы получить семейство эквипотенциальных поверхностей.
Эквипотенциальные поверхности также тесно связаны с силовыми линиями
электрического поля. Если электрический заряд перемещается по эквипотенциальной
поверхности, то работа поля равна нулю, так работа по перемещению заряда q
пропорциональна изменению потенциала δA = − q∆ϕ , а на эквипотенциальной
поверхности ∆ϕ = 0 . С другой стороны эта работа выражается через напряженность поля
r
r r
r
E как δA = qE ⋅ ∆r = qE∆r cos α (где ∆r - вектор перемещения заряда, α - угол между
векторами напряженности поля и перемещения). Если вектор перемещения направлен
вдоль эквипотенциальной поверхности, то работа поля
равна нулю, следовательно, вектор напряженности в этом
случае перпендикулярен вектору перемещения (косинус
прямого угла равен нулю). Таким образом, силовые
линии электростатического поля перпендикулярны
эквипотенциальным поверхностям (Рис. 188). Если же
вектор перемещения направлен вдоль силовой линии, то
изменение
потенциала
будет
максимальным,
следовательно, силовые линии указывает направления
максимального изменения (точнее уменьшения) потенциала.
На рисунке 189 показаны одновременно семейства силовых линий и семейство
эквипотенциальных поверхностей поля двух точечных зарядов, рассмотренных ранее.
135
9.11 Примеры расчета потенциалов электростатических полей.
Поле равномерно заряженной сферы. Пусть
электрическое поле создается зарядом Q , равномерно
распределенным по поверхности сферы радиуса R
(Рис. 190). Для вычисления потенциала поля в
произвольной точке, находящейся на расстоянии r от
центра сферы, необходимо вычислить работу,
совершаемую полем при перемещении единичного
положительного заряда от данной точки до
бесконечности. Ранее мы доказали, что напряженность
поля равномерно заряженной сферы вне ее эквивалентно полю точечного заряда,
расположенного в центре сферы. Следовательно, вне сферы потенциал поля сферы будет
совпадать с потенциалом поля точечного заряда
Q
ϕ (r ) =
.
(1)
4πε 0 r
Q
. Внутри сферы
В частности, на поверхности сферы потенциал равен ϕ 0 =
4πε 0 R
электростатическое поле отсутствует, поэтому работа по перемещению заряда из
произвольной точки, находящейся внутри сферы, на ее поверхность равна нулю A = 0 ,
поэтому и разность потенциалов между этими точками
также равна нулю ∆ϕ = − A = 0 . Следовательно, все
точки внутри сферы имеют один и тот же потенциал,
совпадающий с потенциалом ее поверхности
Q
ϕ0 =
.
4πε 0 R
Итак, распределение потенциала поля равномерно
заряженной сферы имеет вид (Рис. 191)
⎧ Q
⎪ 4πε R , при r < R
⎪
0
ϕ (r ) = ⎨
.
(2)
Q
⎪
, при r > R
⎪⎩ 4πε 0 r
Обратите внимание, поле внутри сферы отсутствует, а потенциал отличен от нуля! Этот
пример является яркой иллюстрацией, того, что потенциал определяется значением поля
от данной точки до бесконечности.
Поле равномерно заряженного кольца. Вычислим потенциал
поля, создаваемого зарядом Q , равномерно распределенным по
тонкому кольцу радиуса R , причем ограничимся расчетом
потенциала поля только на оси кольца (Рис. 192).
Ранее
мы
вычислили напряженность поля на оси кольца, как функцию
расстояния до его центра . Поэтому для вычисления потенциала
можно, в принципе, подсчитать работу, совершаемую полем при
перемещении заряда от данной точки до бесконечности. Однако, в
данном случае проще воспользоваться принципом суперпозиции
для потенциала поля. Для этого мысленно разобьем кольцо на малые участки, несущие
заряд ∆Qk . Тогда в точке, находящейся на расстоянии z от его центра, этот заряд создает
поле, потенциал которого равен
136
δϕ k =
∆Qk
∆Qk
=
.
4πε 0 r 4πε 0 R 2 + z 2
Так как все точки кольца находятся на одинаковом расстоянии r = R 2 + z 2 от
рассматриваемой точки, то суммирование потенциалов полей, создаваемых зарядами ∆Qk
сводится к суммированию самих зарядов
∆Qk
1
Q
.
(3)
ϕ=
δϕ k =
=
∆Qk =
2
2
4πε 0 R 2 + z 2 k
4πε 0 R 2 + z 2
k
k 4πε 0 R + z
График этой функции показан на рисунке. Там же повторен график зависимости
напряженности поля кольца на его оси от расстояния до центра кольца. Напомним, что
значения потенциала ϕ ( z 0 ) в точке с координатой z 0 численно равно площади под
графиком зависимости E ( z ) в интервале от z 0 до z → ∞ .
∑
∑
∑
Обратите внимание – так как проекция вектора напряженности не изменяет свой знак, то
функция ϕ ( z ) является монотонной.
Поле равномерно заряженной бесконечной пластины. Ранее мы показали, что
электрическое поле, создаваемое бесконечной равномерно заряженной пластиной
является однородным, то есть напряженность поля одинакова во всех точках, причем
вектор напряженности направлен перпендикулярно плоскости, а его модуль равен
E0 =
σ
. Семейством силовых линий такого поля явяется набор параллельных прямых,
2ε 0
перпендикулярных пластине. На рис. 194 так же изображен график зависимости проекции
вектора напряженности поля E z на ось Z перпендикулярную пластине (начало отсчета
этой оси расположим на пластине). Понятно, что потенциал данного поля зависит только
от координаты z , то есть эквипотенциальные поверхности в данном случае являются
плоскостями, параллельными заряженной пластине.
137
При традиционном выборе нулевого уровня потенциала ϕ ( z → ∞ ) = 0 , потенциал
произвольной точки равен работе по перемещению единичного положительного заряда из
данной точки на бесконечность. Так как модуль напряженности постоянен, то такая
работа (а, следовательно, и потенциал) оказывается равной бесконечности!
Следовательно, указанный выбор нулевого уровня потенциала в данном случае
непригоден.
Поэтому следует воспользоваться произволом выбора
нулевого уровня. Достаточно выбрать произвольную точку с
координатой z = z 0 , и приписать ей произвольное значение
потенциала ϕ ( z 0 ) = ϕ 0 (Рис. 195). Теперь, чтобы вычислить
значение потенциала в произвольной точке ϕ ( z ) , можно
воспользоваться соотношением между напряженностью и
r r
потенциалом поля ∆ϕ = − E ⋅ ∆r . Учитывая, что в данном случае
напряженность поля постоянна (при z > 0 ) это выражение
записывается в виде
ϕ (z 0 ) − ϕ (z ) = − E0 (z 0 − z ) ,
из которого следует искомая зависимость
потенциала от координаты (при z > 0 )
ϕ (z ) = ϕ 0 − E0 (z − z 0 )
(4)
В частности, можно задать произвольное значение
потенциала самой пластины, то есть положить
при
z = z0 = 0
ϕ = ϕ 0 . Тогда значение
потенциала в произвольной точке определяется
функцией
ϕ (z ) = ϕ 0 − E0 z ,
(5)
график которой показан на рисунке 196.
То, что потенциал относительно бесконечности оказался бесконечно большим, вполне очевидно –
ведь и бесконечная пластина обладает бесконечно большим зарядом. Как мы уже подчеркивали, такая
система является идеализацией – бесконечных пластин не существует. В реальности все тела имеют
конечные размеры, поэтому для них традиционный выбор нулевого потенциала возможен, правда в этом
случае распределение поля может быть очень сложным. В рамках же рассматриваемой идеализации удобнее
воспользоваться использованным нами выбором нулевого уровня.
Задание для самостоятельной работы.
1. Покажите, что при произвольном выборе нулевого уровня потенциала функция (4)
может быть обобщена на все значения координаты z (в том числе и отрицательные)
следующим образом
ϕ (z ) = ϕ 0 − E0 ( z − z 0 ) .
Постройте график этой функции.
Поле двух параллельных равномерно заряженных
пластин.
Найдем
распределение
потенциала
поля,
создаваемого двумя одинаковыми равномерно заряженными
параллельными пластинами, заряды которых равны по модулю
и
противоположны по знаку1 (Рис. 197). Обозначим
поверхностную плотность заряда на одной пластине + σ , а на
другой − σ . Расстояние между пластинами h будем считать значительно меньшим
размеров пластин. Введем систему координат, ось z которой перпендикулярна
1
Такая система называется плоским конденсатором, подробнее эти устройства мы будем изучать позже.
138
пластинам, начало координат разместим по средине между пластинами. Очевидно, для
бесконечно больших пластин все характеристики поля (напряженность и потенциал)
зависят только от координаты z . Для расчета напряженности поля в различных точках
пространства воспользуемся полученным выражением для напряженности поля,
создаваемого бесконечной равномерно заряженной пластиной и принципом
суперпозиции.
Каждая равномерно заряженная пластина создает однородное поле, модуль
напряженности которого равен E 0 =
σ
, а направления указаны на рисунке 198.
2ε 0
Складывая напряженности полей по принципу суперпозиции, получим, что в
пространстве между пластинами напряженность поля E = 2 E 0 =
σ
вдвое превышает
ε0
напряженность поля одной пластины (здесь поля отдельных пластин параллельны), а вне
пластин поле отсутствует (здесь поля отдельных пластин противоположны).
Строго говоря, для пластин конечных
размеров поле не является однородным,
силовые линии поля пластин конечных
размеров показаны на рисунке 199. Наиболее
сильные
отклонения
от
однородности
наблюдаются вблизи краев пластин (часто эти
отклонения называют краевыми эффектами).
Однако, в области прилегающей к середине
пластин поле с высокой степенью точности
можно считать однородным, то есть в этой области можно пренебречь краевыми эффектами. Заметим, что
погрешности такого приближения тем меньше, чем меньше отношение расстояния между пластинами к их
размерам.
Для
однозначного
определения
распределения
потенциала поля, необходимо выбрать уровень нулевого
потенциала. Будем считать, что потенциал равным нулю в
плоскости расположенной по средине между пластинами, то
есть, положим ϕ = 0 при z = 0 .
Не смотря на произвол в выборе нулевого уровня потенциала, наш
выбор может быть логически обоснован на основании симметрии системы.
Действительно, рассматриваемая система зарядов зеркально повторяет себя
при зеркальном отражении относительно плоскости z = 0 и одновременном
изменении знаков зарядов. Поэтому желательно, чтобы и распределение
потенциала обладало такой же симметрией: восстанавливалось при
зеркальном отражении с одновременным изменением знака всех функций
поля. Выбранный нами способ выбора нулевого потенциала удовлетворяет такой симметрии.
Обозначим потенциал положительно заряженной пластины + ϕ 0 , тогда потенциал
отрицательно заряженной пластины будет равен − ϕ 0 . Эти потенциалы легко определить,
используя найденное значение напряженности поля между пластинами и связь между
139
напряженностью и разностью потенциалов электрического поля. Уравнение этой связи в
данном случае имеет вид ϕ 0 − (− ϕ 0 ) = Eh . Из этого соотношения определяем значения
σh
потенциалов пластин ϕ 0 =
. Учитывая, что между пластинами поле однородное
2ε 0
(поэтому потенциал изменяется линейно), а вне пластин поле отсутствует (поэтому здесь
потенциал постоянен), зависимость потенциала
от координаты z имеет вид (рис. 201)
h
⎧
⎪+ ϕ 0 , при z < − 2
⎪
h
h
⎪ ϕ
ϕ ( z ) = ⎨− 2 0 z, при − < z < + .
h
2
2
⎪
h
⎪
⎪− ϕ 0 , при z > + 2
⎩
(6)
Задания для самостоятельной работы.
1. Во всех рассмотренных примерах проделайте обратную операцию: по найденному
∆ϕ
рассчитайте напряженности
распределению потенциала с помощью формулы E x = −
∆x
рассмотренных полей.
2. Строго выведите формулу (6).
3. Качественно объясните следующий «парадокс». В поле плоского конденсатора
неоднозначно определен потенциал «бесконечности»: при движении в положительном
направлении оси Z потенциал «бесконечности» оказался равным − ϕ 0 ; при движении в
отрицательном направлении оси Z - + ϕ 0 , при движении вдоль осей X или Y - равен
нулю. Так чему равен потенциал «бесконечности» в реальной системе двух пластин
конечных размеров?
9.12 Электрический диполь.
Часто возникает необходимость найти характеристики электрического поля,
создаваемого системой зарядов, локализованных в небольшой области пространства.
Примером такой системы зарядов могут служить атомы и молекулы, состоящие из
электрически заряженных ядер и электронов. Если требуется найти поле на расстояниях,
которые значительно больше размеров области расположения частиц, то нет
необходимости пользоваться точными, но громоздкими формулами, достаточно
ограничится более простыми приближенными выражениями.
Пусть электрическое поле создается набором
точечных зарядов q k (k = 1,2...N ) , расположенных
в
пределах небольшой области пространства, характерные
размеры которой обозначим l (Рис. 202). Для расчета
характеристик электрического поля, в некоторой точке A ,
находящейся на расстоянии r , значительно превышающем
l , все заряды системы можно «объединить» и рассматривать
систему зарядов как точечный заряд Q , величина которого
равна сумме зарядов исходной системы
140
N
Q = q1 + q2 + ... + q N =
∑q
(1)
k
k =1
Этот заряд можно мысленно расположить в любой точке области расположения системы
зарядов q k (k = 1,2...N ) , так как при l << r , изменение положения в пределах малой
области незначительно повлияет на изменение поля в рассматриваемой точке.
В рамках такого приближения напряженность и потенциал электрического поля
определяются по известным формулам
Q
Q
E=
,
ϕ=
.
(2)
2
4πε 0 r
4πε 0 r
Если суммарный заряд системы равен нулю, то указной приближение является
слишком грубым, приводящим к выводу об отсутствии электрического поля.
Более точное приближение можно получить, если мысленно собрать отдельно
положительные и отрицательные заряды рассматриваемой системы. Если их «центры»
смещены друг относительно друга, то электрическое поле такой системы может быть
описано как поле двух точечных зарядов, равных по величине и противоположных по
знаку, смещенных друг относительно друга. Более точную характеристику системы
зарядов в этом приближении мы дадим немного позднее, после изучения свойств
электрического диполя.
Электрическим диполем называется система, состоящая из двух точечных
зарядов одинаковых по величине и противоположных по знаку, расположенных на
малом расстоянии друг от друга.
Рассчитаем
характеристики
электрического поля, создаваемого диполем,
состоящего из двух точечных зарядов + q и − q ,
расположенных на расстоянии a друг от друга
(Рис. 203). Сначала найдем потенциал и напряженность электрического поля диполя на
его оси, то есть на прямой, проходящей через оба заряда. Пусть точка A , находится на
расстоянии r от центра диполя, причем будем считать, что r >> a . В соответствии с
принципом суперпозиции потенциал поля в данной точке описывается выражением
q
q
q
a
qa
ϕ=
=
⋅
≈
.
(3)
−
2
a⎞
a ⎞ 4πε 0 2 ⎛ a ⎞
4πε 0 r 2
⎛
⎛
4πε 0 ⎜ r − ⎟ 4πε 0 ⎜ r + ⎟
r −⎜ ⎟
2⎠
2⎠
⎝
⎝
⎝ 2⎠
2
⎛a⎞
На последнем шаге мы пренебрегли вторым малой величиной ⎜ ⎟ по сравнению с r 2 .
⎝ 2⎠
Величину вектора напряженности электрического поля также можно вычислить на
основании принципа суперпозиции
q
q
q
2ar
qa
.
(4)
−
=
⋅
E=
≈
2
2
2
3
2
4πε 0 ⎛
2
πε
r
a⎞
a⎞
⎛
⎛
⎞
0
4πε 0 ⎜ r − ⎟
4πε 0 ⎜ r + ⎟
⎜ r 2 − ⎛⎜ a ⎞⎟ ⎟
2
2
⎜
⎝
⎠
⎝
⎠
⎝ 2 ⎠ ⎟⎠
⎝
Напряженность поля можно вычислить, используя соотношение между потенциалом и
∆ϕ
напряженностью поля E x = −
. В данном случае вектор напряженности направлен
∆x
вдоль оси диполя, поэтому его модуль рассчитывается следующим образом
141
qa 1 ⎛
∆ϕ
1
1⎞
ϕ (r + ∆r ) − ϕ (r )
⎜
⎟=
=−
=−
−
2
4πε 0 ∆r ⎜⎝ (r + ∆r )
∆r
∆r
r 2 ⎟⎠
.
(5)
2
qa 1 − 2r∆r − (∆r )
qa
=−
≈
4πε 0 ∆r r 2 (r + ∆r )2
2πε 0 r 3
Обратите внимание, что поле диполя ослабевает быстрее поля точечного заряда, так
потенциал поля диполя убывает обратно пропорционально квадрату расстояния, а
напряженность поля - обратно пропорционально кубу расстояния.
E=−
Аналогичным, но более громоздким, способом можно найти
потенциал и напряженность поля диполя в произвольной точке,
положение которой определим с помощью полярных координат:
расстояния до центра диполя r и угла θ (Рис. 204). По принципу
суперпозиции потенциал поля в точке A равен
ϕ=
q
q
−
=
q
⋅
(r− − r+ ) .
r− r+
4πε 0 r+ 4πε 0 r− 4πε 0
Учитывая, что r >> a , формулу (6) можно упростить с помощью
2
приближений r− r+ ≈ r , r− − r+ ≈ a cosθ , в этом случае получаем
qa cosθ
ϕ=
.
4πε 0 r 2
r
Вектор напряженности электрического поля E удобно
r
разложить на две составляющие: радиальную E r , направленную
(6)
вдоль прямой, соединяющей данную точку с центром диполя, и
r
перпендикулярную ей Eθ (рис. 205). При таком разложении каждая
компонента направлена вдоль направления изменения каждой из
координат точки наблюдения, поэтому может быть найдена из
соотношения, связывающего напряженность поля и изменение
потенциала.
Для того, чтобы найти компоненты вектора напряженности поля, запишем отношение изменения
потенциала, при смещении точки наблюдения в направлении
соответствующих векторов (Рис. 206).
Радиальная составляющая тогда выразится соотношением
qa cosθ 1 ⎛
∆ϕ
ϕ (r + ∆r ) − ϕ (r )
1
1⎞
⎜
=−
=−
− 2 ⎟⎟ =
2
⎜
∆r
∆r
4πε 0 ∆r ⎝ (r + ∆r )
r ⎠
.
2
qa cosθ 2r∆r + (∆r )
qa cosθ
=
≈
4πε 0 ∆r (r + ∆r )2 r 2
2πε 0 r 3
Er = −
Для расчета перпендикулярной составляющей следует учесть, что величина
малого смещения в перпендикулярном направлении выражается через
изменение угла следующим образом ∆l = r∆θ . Поэтому величина этой
компоненты поля равна
Eθ = −
=
qa cos(θ + ∆θ ) − cosθ
ϕ (θ + ∆θ ) − ϕ (θ )
∆ϕ
=
=−
=−
r∆θ
r∆θ
∆θ
4πε 0 r 3
qa sin θ sin ∆θ qa sin θ
≈
4πε 0 r 3 ∆θ
4πε 0 r 3
При выводе последнего соотношения использована тригонометрическая формула для разности косинусов и
приближенное соотношение, справедливое при малых ∆θ : sin ∆θ ≈ ∆θ .
142
Полученные соотношения полностью определяют поле диполя в
произвольной точке и позволяют построить картину силовых линий
этого поля (рис. 207).
Теперь обратим внимание, что во всех формулах,
определяющих потенциал и напряженность поля диполя,
фигурирует только произведение величины одного из
зарядов диполя на расстояние между зарядами. Поэтому
именно это произведение является полной характеристикой
электрических свойств и называется дипольным моментом системы. Так как диполь
является системой двух точечных зарядов, то он обладает осевой симметрией, осью
которой является прямая, проходящая через заряды. Следовательно, для задания полной
характеристики диполя следует указать и ориентацию оси диполя. Проще всего это
сделать, задавая вектор дипольного момента, величина которого равна дипольному
моменту, а направление совпадает с осью диполя
r
r
(7)
p = qa ,
r
2
где a - вектор, соединяющий отрицательный и положительный заряды диполя . Такая
характеристика диполя весьма удобна и позволяет во многих случая упрощать формулы,
придавая им векторный вид. Так, например, потенциал поля диполя в произвольной точке,
описываемый формулой (6), может быть записан в векторной форме
r r
p⋅r
ϕ=
.
(8)
4πε 0 r 3
После введения векторной характеристики диполя, его дипольного момента, появляется
возможность использовать еще одну упрощающую модель – точечный диполь: систему
зарядов, геометрическими размерами которой можно пренебречь, но обладающей
дипольным моментом3.
Рассмотрим поведение диполя в электрическом поле.
Пусть два точечных заряда, находящиеся на фиксированном
расстоянии друг от друга, помещены в однородное электрическое
поле. Со стороны поля на заряды действуют силы F = ± qE ,
равные по величине и противоположные по направлению.
Суммарная сила, действующая на диполь равна нулю, однако эти
силы приложены к различным точкам, поэтому суммарный
момент этих отличен от нуля, а равен
M = Fa sin α = qEa sin α = pE sin α ,
(9)
где α - угол меду вектором напряженности поля и вектором дипольного момента.
Наличие момента силы, приводит к тому, что дипольный момент системы стремится
повернуться по направлению вектора напряженности электрического поля.
Обратите внимание, что и момент силы, действующий на диполь, полностью определяется его
дипольным моментом. Как мы показали ранее, если сумма сил, действующих на систему, равна нулю, то
суммарный момент сил не зависит от оси, относительно которой этот момент рассчитывается. Положению
равновесия диполя соответствуют как направление по полю α = 0 , так и против него α = π , однако легко
показать, что первое положение равновесия устойчиво, а второе нет.
Если электрический диполь находится в неоднородном электрическом поле, то
силы, действующие на заряды диполя различны, поэтому результирующая сила отлична
от нуля.
2
Направление вектора дипольного момента, в принципе можно задать и противоположным, но исторически
сложилось задание направления дипольного момента от отрицательного к положительному заряду. При
таком определении силовые линии как бы являются продолжением вектора дипольного момента.
3
Очередная, абсурдная на первый взгляд, но удобная абстракция – материальная точка, имеющая два
заряда, разнесенных в пространстве.
143
Для упрощения, будем считать, что ось диполя
совпадает с направлением вектора напряженности
внешнего электрического поля. Совместим ось x
системы
координат
с
направлением
вектора
напряженности (Рис. 209). Результирующая сила,
действующая на диполь, равна векторной сумме сил,
действующих на заряды диполя,
∆E
.
(10)
∆x
Здесь E ( x ) - напряженность поля в точке расположения отрицательного заряда, E ( x + a ) напряженность в точке положительного заряда. Так как расстояние между зарядами мало,
разность напряженностей представлена как произведение скорости изменения
напряженности на размер диполя. Таким образом, в неоднородном поле, на диполь
действует сила, направлена в сторону возрастания поля, или диполь втягивается в область
более сильного поля.
В заключение вернемся к строгому определению
дипольного момента произвольной системы зарядов. Вектор
дипольного момента, системы, состоящей из двух зарядов (Рис.
210), может быть записан в виде
r
r
r
r
r
r
p = qa = q (r+ − r− ) = (+ q )r+ + (− q )r− .
Если теперь пронумеровать заряды, то эта формула приобретает
вид
r
r
r
r
r
p = (+ q )r+ + (− q )r− = q1 r1 + q 2 r2 ,
где величины зарядов понимаются в алгебраическом смысле, с
учетом их знаков. Последняя формула допускает очевидное обобщение (обоснованием
которого является принцип суперпозиции) на систему произвольного числа зарядов
r
r
r
r
r
p = q1 r1 + q 2 r2 + q3 r3 + ... =
q k rk .
(11)
F = F+ − F− = q(E ( x + a ) − E ( x )) = qa
∑
k
Эта формула определяет дипольный момент
произвольной системы зарядов, с ее помощью произвольная
система зарядов может быть заменена на точечный диполь
(Рис. 211). Положение диполя внутри области расположения
зарядов произвольно, естественно, если электрическое поле
рассматривается на расстояниях значительно превышающих
размеры системы.
Задания для самостоятельной работы.
1. Докажите, что для произвольной системы зарядов, алгебраическая сумма которых
равна нулю, дипольный момент, определяемый по формуле (11), не зависит от выбора
системы отсчета.
2. Определите «центры» положительных и отрицательных зарядов системы, по
формулам аналогичным, формулам для координат центра масс системы. Если все
положительный и все отрицательные заряды собрать в своих «центрах», то получим
диполь, состоящий из двух зарядов. Покажите, что его дипольный момент совпадает с
дипольным моментом, рассчитанным по формуле (11).
3. Получите двумя способами формулу, выражающую силу взаимодействия точечного
диполя и точечного заряда, находящегося на оси диполя: во-первых, найдите силу,
действующую на точечный заряд со стороны диполя; во-вторых, найдите силу,
действующую на диполь со стороны точечного заряда; в-третьих, убедитесь, что эти
силы равны по модулю и противоположны по направлению.
144
9.13 Энергия электрического поля. Плотность энергии.
Вернемся к обсуждению вопроса об энергии взаимодействия
электрических зарядов. Ранее мы показали, что потенциальная энергия
электростатического взаимодействия двух точечных зарядов q1 и q 2 ,
находящихся на расстоянии r друг от друга (рис. 212), рассчитывается
по формуле
1 q1 q 2
.
U (r ) =
4πε 0 r
Придадим этой формуле несколько иной вид
⎛ 1 q2 ⎞
1 q1 q 2
⎟⎟ = q1ϕ 1 ,
U (r ) =
= q1 ⎜⎜
4πε 0 r
⎝ 4πε 0 r ⎠
(1)
q2
- потенциал поля, создаваемого вторым зарядом, в точке, где находится
4πε 0 r
первый заряд. Аналогично можно записать
⎛ 1 q1 ⎞
1 q1 q 2
⎟⎟ = q 2ϕ 2 ,
= q 2 ⎜⎜
U (r ) =
πε
r
4πε 0 r
4
0
⎝
⎠
1
здесь ϕ1 =
q1
- потенциал поля, создаваемого первым зарядом, в точке, где находится
4πε 0 r
второй заряд. Теперь, перепишем выражение (1), в симметричной форме, легко
допускающей обобщение
1
U (r ) = (q1ϕ1 + q 2ϕ 2 ) .
(2)
2
где ϕ 2 =
1
В этой формуле мы выписали два равных слагаемых, каждое из которых можно трактовать как
энергию взаимодействия одного из зарядов с другим, но мы подчеркивали, что энергия взаимодействия, не
«принадлежит» ни одному из зарядов, поэтому нельзя учитывать эту энергию дважды – из-за этого и
появляется в формуле множитель 1 / 2 .
Если система состоит из нескольких зарядов q1 , q 2 ...q k ... (k = 1,2...N ) , то полная
энергия их взаимодействия есть сумма энергий взаимодействий всех пар зарядов.
Используя симметричное выражение (2), суммирование по парам зарядов (двойную
сумму), можно заменить на суммирование по самим зарядам, то есть записать
1 qi q k 1
1
U=
= (q1ϕ 1 + q 2ϕ 2 + ...q k ϕ k + ...) =
qkϕ k
(3)
4πε 0 rik
2
2 по зарядам
по парам
∑
∑
В этой формуле ϕ k - потенциал поля в точке, где находится заряд q k , причем поля,
создаваемого всеми зарядами,
кроме самого заряда q k (как говорят, исключая
самовоздействие заряда на самого себя).
Использование понятия энергии взаимодействия требует чрезвычайной точности и
внимательности. Произвол в выборе нулевого уровня энергии, с одной стороны,
предоставляет определенную свободу, а, с другой, требует четкого понимания о какой
именно энергии идет речь. Так, если в формуле (3) потенциалы отсчитываются
относительно точек, бесконечно удаленных от зарядов, то эта формула определяет работу,
которую совершит электрическое поле при удалении всех зарядов на бесконечно большие
расстояния друг от друга. Если же требуется рассчитать работу поля при изменении
положения зарядов, то выбор нулевого уровня не принципиален – эта работа не зависит от
нулевого уровня потенциала.
Для того чтобы разобраться в некоторых нюансах применения формулы (3),
рассмотрим примеры расчета энергии электростатического взаимодействия.
145
Три точечных заряда.
Пусть три одинаковых точечных заряда, величины которых
равны между собой q1 = q 2 = q3 = q , расположены в вершинах
правильного треугольника со стороной a (рис.213). Для расчета
энергии взаимодействия этих зарядов заметим, что все заряды
равноправны, находятся в одинаковых условиях. В месте
расположения одного из зарядов потенциал поля, создаваемого
двумя другими зарядами равен
q
ϕ1 = ϕ 2 = ϕ 3 = 2
.
4πε 0 a
В соответствии с формулой (3) энергия взаимодействия зарядов равна
1
q2
U 0 = (q1ϕ1 + q 2ϕ 2 + q3ϕ 3 ) = 3
.
(4)
2
4πε 0 a
Такую работу совершит электрическое поле, при удалении всех зарядов на бесконечное
расстояние друг от друга.
Если заряды сместятся, так что окажутся в вершинах
правильного треугольника со стороной a1 , то их энергия
окажется равной
q2
U1 = 3
.
4πε 0 a1
При таком смещении работа электрического поля будет равна
уменьшению энергии системы
q2 ⎛ 1 1 ⎞
⎜ − ⎟.
A = U 0 − U1 = 3
4πε 0 ⎜⎝ a a1 ⎟⎠
Обратите внимание, при a1 → ∞ эта работа становится в точности равной начальной
энергии U 0 .
Если из первоначальной системы мы удалим один заряд
при неподвижных оставшихся (рис. 215), то энергия системы
станет равной
q2
U1 =
,
4πε 0 a
При этом поле совершит работу
q2
q2
q2
A1 = U 0 − U 1 = 3
−
=2
.
4πε 0 a 4πε 0 a
4πε 0 a
Если теперь удалить еще один заряд, то энергия системы станет
равной нулю, при этом поле совершит работу A2 = U 1 . В итоге
начальная энергия полностью расходуется на совершение
полной работы U 0 = A1 + A2 .
Задание для самостоятельной работы.
1. Проанализируйте изменение энергии и совершенные работы в рассмотренной системе,
если один из зарядов отрицательный.
146
Энергия взаимодействия двух равномерно заряженных параллельных пластин.
Найдем энергию взаимодействия двух равных по
модулю зарядов противоположного знака, равномерно
распределенными по двум параллельным пластинам.
Обозначим поверхностную плотность заряда на одной
пластине + σ , а на другой
− σ . Расстояние между
пластинами h будем считать значительно меньшим
размеров пластин, площадь каждой пластины обозначим S .
Краевыми эффектами пренебрежем.
Для расчета энергии взаимодействия воспользуемся формулой U = qϕ ′ , где ϕ ′ потенциал поля создаваемого всеми зарядами, кроме заряда q .
Напряженность поля между пластинами была вычислена нами
ранее, она равна
E=
σ
.
ε0
(5)
Для «упрощения» расчетов положим потенциал отрицательно
заряженной пластины равным нулю, тогда потенциал другой
пластины будет равен
r r
σh
ϕ = − E ⋅ ∆r = Eh = ,
(6)
ε
0
r
Здесь ∆r - вектор перемещения от отрицательной пластины к положительной. Данная
формула определяет потенциал поля, создаваемого зарядами на обеих пластинах.
Теперь необходимо найти потенциал поля ϕ ′ , создаваемого только одной
пластиной. Напряженность поля E ′ , создаваемого одной пластиной в два раза меньше
E
σ
, поэтому искомый потенциал будет
напряженности поля между пластинами E ′ = =
2 2ε 0
σh
равен ϕ ′ = E ′h =
. Таким образом, энергия взаимодействия зарядов оказывается
2ε 0
равной
σh σ 2
U = qϕ ′ = (σS )
=
Sh ,
(7)
2ε 0 2ε 0
здесь σS - заряд положительно заряженной пластины.
Не смотря на то, что противоположно заряженные пластины притягиваются, их энергия оказалась
положительной – в этом нет ничего удивительного: мы положили потенциал одной из пластин равным
нулю. Это значит, что нулевой энергии соответствует положение, когда положительно заряженная пластина
совпадает с отрицательно заряженной, то есть когда пластины совпадают, а электрическое поле отсутствует.
Если пластины находятся на некотором расстоянии h друг от друга, то при их сближении поле совершит
положительную работу. Наоборот, чтобы разнести пластины, внешние силы должны совершить работу,
увеличивая энергию системы.
Энергию рассматриваемой системы можно найти,
рассчитывая работу внешних сил, по разнесению пластин.
На одну из пластин со стороны другой действует сила
электрического притяжения
F = qE ′ = (σS )
σ
σ2
=
S,
2ε 0 2ε 0
причем эта сила не зависит от расстояния между
пластинами. Для того, чтобы раздвинуть пластины на расстояние h , необходимо
приложить внешнюю силу, равную по модулю силе электрического притяжения (рис.
218). При этом эта сила совершит работу (равную увеличению энергии системы)
147
A = U = Fh =
σ2
Sh .
2ε 0
(7’)
Таким образом, мы получаем ту же формулу для энергии систему зарядов.
Используя соотношение между напряженностью поля между пластинами и поверхностной
плотностью заряда σ = ε 0 E , выразим энергию взаимодействия через напряженность поля
U=
ε0E 2
Sh .
(8)
2
В процессе разнесения пластин создается электрическое поле во все большем
объеме между пластинами, поэтому можно утверждать, что совершенная работа
увеличивает энергию электрического поля, или работа расходуется на создание поля. Так
при смещении пластины на расстояние ∆z , объем занятый полем увеличивается на S∆z ,
если расстояние между пластинами увеличилось от нуля до некоторого значения h , то
поле создается в объеме Sh . Таким образом, найденная энергия взаимодействия зарядов
(7) есть энергия электрического поля - энергия «размазанная» по той области
пространства, где создано поле. Косвенным подтверждением сделанного заключения,
является тот факт, что энергия взаимодействия пропорциональна объему части
пространства V = Sh , занятого полем и выражается через характеристику поля (его
напряженность) – в формуле (8) нет характеристик зарядов. Электрическое поле, уже
благодаря своему существованию обладает энергией. В качестве энергетической
характеристики поля следует рассматривать энергию, содержащуюся в единице объема,
U
то есть объемную плотность энергии: w = . Из выражения (8) следует, что объемная
V
плотность энергии электрического поля определяется формулой
ε E2
(9)
w= 0 .
2
Как обычно, в неоднородном поле корректное определение плотности энергии «в данной точке»
требует предельного перехода: плотностью энергии электрического поля называется отношение энергии
поля, заключенной в малом объеме к величине этого объема, при стремлении последнего к нулю
w=
∆U
, при ∆V → 0 .
∆V
Энергия поля равномерно заряженной сферы.
Пусть электрический заряд Q равномерно распределен по
поверхности сферы радиуса R . Вне сферы электрическое поле,
создаваемое зарядами на сфере, эквивалентно полю точечного
заряда, помещенного в центре сфере (рис. 219). Внутри сферы поле
отсутствует. Так напряженность поля в точке, находящейся на
расстоянии r от центра сферы равна
Q
,
(10)
E (r ) =
4πε 0 r 2
в частности непосредственно у поверхности сферы напряженность поля равна
Q
.
E0 =
4πε 0 R 2
(11)
Обратим внимание, что произведение S = 4πR 2 есть площадь сферы, поэтому отношение
Q
= σ является поверхностной плотностью заряда на сфере, поэтому напряженность
4πε 0
поля у поверхности сферы выражается той же формулой, что и напряженность поля
148
между пластинами, рассмотренными в предыдущем разделе E 0 =
σ
.
ε0
Потенциал
поверхности сферы также был вычислен нами ранее
Q
.
(12)
ϕ0 =
4πε 0 R
Рассчитаем теперь энергию поля, создаваемого зарядами на
сфере. Мысленно разделим заряд сферы на N равных малых частей
Q
(рис.220), величины которых равны δQk = , (k = 1,2...N ) . Рассмотрим
N
один из этих малых зарядов. В точке его расположения потенциал поля,
(N − 1)δQ .
создаваемого всеми остальными (N − 1) зарядами равен ϕ k =
4πε 0 R
1
q k ϕ k , выражение для энергии
С использованием симметричной формулы U =
2 k
∑
взаимодействия приобретает вид
1
U=
2
∑
k
1
qkϕ k =
2
N
∑ δQ
k =1
k
(N − 1)δQ ,
4πε 0 R
данная сумма содержит N одинаковых слагаемых, поэтому равна
N
∑
(N − 1)δQ = 1 NδQ (N − 1)δQ = 1 N (N − 1) (δQ )2
1⎞
Q2 ⎛
δQ k
(13)
=
⎜1 − ⎟ .
4πε 0 R
2
4πε 0 R
2
4πε 0 R 8πε 0 R ⎝ N ⎠
k =1
Так как число частей N , на которые разбивается сфера, может быть сделано сколь угодно
большим, поэтому в пределе N → ∞ слагаемое 1 исчезает, поэтому окончательное
N
выражение для энергии взаимодействия зарядов сферы имеет вид
Q2
.
(14)
U=
8πε 0 R
1
Заметим, что полученное выражение имеет вид U = Qϕ 0 . Если сразу заявить, что уменьшение
2
заряда на малую величину δQ пренебрежимо мало изменяет потенциал сферы, то результат (4) получается
1
U=
2
прямым применением формулы для энергии взаимодействия зарядов. Однако обращение с малыми
величинами требует известной строгости, поэтому мы и привели несколько «удлиненный» вывод.
Приведем еще один вывод этой же формулы. Для этого энергию системы
рассчитаем как работу, которую необходимо совершить, чтобы зарядить сферу. Мысленно
Q
будем заряжать сферу малыми равными порциями заряда δQk = , (k = 1,2...N ) ,
N
которые будем переносить на сферу из «бесконечности». Если сфера не заряжена, то
перенесение первой «порции» заряда не требует совершения никакой работы. После того
как сфера приобрела некоторый электрический заряд, перенесение следующей порции
заряда требует совершения работы по преодолению сил отталкивания со стороны зарядов
сферы. Если на сферу перенесено (k − 1) порций заряда, то ее потенциал равен
(k − 1)δQ . Поэтому для того, что бы перенести на сферу следующую порцию
ϕ (k −1) =
4πε 0 R
заряда необходимо совершить работу
(δQ )2 .
Ak = δQϕ (k −1) = (k − 1)
4πε 0 R
Заметьте, что для перенесения каждой следующей порции заряда надо совершать большую работу.
149
Полная работа по зарядке сферы (равная энергии электрического поля сферы) выражается
суммой геометрической прогрессии
N ( N − 1)
Q2 ⎛
1⎞
(15)
=
⎜1 − ⎟ .
πε
R
πε
R
πε
R
N
4
4
2
8
⎠
⎝
0
0
0
k =1
k =1
Как и следовало ожидать, мы получили выражение, полностью совпадающее с (13), при
бесконечном уменьшении порций переносимых зарядов (N → ∞ ) мы опять приходим к
формуле (14).
N
U = A=
∑
Ak =
(δQ )2
(δQ )2
(
)
k
1
−
=
∑
N
В этом нет ничего удивительного, так как в первом случае мы подсчитали энергию, которая
выделится при разбегании зарядов со сферы, а во втором – энергию, которую необходимо затратить, чтобы
собрать их обратно.
Покажем, что энергию взаимодействия зарядов и в этом случае можно истолковать
как энергию электрического поля, «размазанную» по всему пространству, где существует
поле. Представим, что радиус сферы увеличился на малую величину ∆R , а ее заряд при
этом не изменился. Согласно формуле (14) энергия взаимодействия зарядов при этом
уменьшится. В пространстве вне сферы увеличенного радиуса
электрическое поле не изменилось, а в тонком сферическом слое между
начальной и расширенной сферами – исчезло (рис. 221)_. Поэтому
следует считать, что уменьшение энергии взаимодействия зарядов при
увеличении радиуса сферы равно энергии, которая заключена в этом
тонком сферическом слое. При малой толщине слоя его объем можно
вычислить как произведение площади сферы на толщину слоя
∆V = 4πR 2 ∆R . Пренебрегая изменением напряженности поля в пределах тонкого слоя,
энергию, заключенную в нем запишем в виде
(16)
∆U = w∆V = 4πR 2 ∆Rw
где w - плотность энергии поля. С другой стороны эта энергия равна изменению энергии
взаимодействия зарядов при увеличении радиуса сферы
Q2
Q2
Q2
∆R
Q 2 ∆R
∆U =
−
=
⋅
≈
⋅
.
8πε 0 R 8πε 0 (R + ∆R ) 8πε 0 R(R + ∆R ) 8πε 0 R 2
На последнем шаге, мы пренебрегли малым изменением радиуса ∆R . Наконец, выразим
заряд шара через напряженность электрического поля у его поверхности Q = 4πε 0 R 2 E :
Q 2 ∆R ε 0 E 2
⋅ 2 =
4πR 2 ∆R .
8πε 0 R
2
Из сравнения с формулой (16) следует, что и в рассматриваемом случае плотность энергии
ε0E2
.
электрического поля выражается формулой w =
2
∆U =
9.14 Энергия поля и энергия взаимодействия зарядов.
Рассмотрим еще раз взаимодействие двух точечных зарядов q1 и q 2 , находящихся
на расстоянии r друг от друга. Мы показали, что энергия их взаимодействия
рассчитывается по формуле
1 q1 q 2
.
(1)
U (r ) =
4πε 0 r
С другой стороны, мы показали, что электрическое поле обладает энергией, объемная
плотность которой определяется формулой
ε0E2
w=
.
(2)
2
Для того чтобы рассчитать полную энергию электрического поля W ,
напряженность которого изменяется от точки к точке, необходимо разбить пространство,
150
где существует поле на малые объемы ∆Vk , в каждом из
которых вычислить плотность энергии поля wk (если
изменяется напряженность поля, то изменяется и его
плотность энергии), после чего просуммировать энергию
по всему пространству, где существует поле
W =
w k ∆V k .
(3)
∑
k
Выполнить такое суммирование не всегда просто, но, тем не менее, такая операция вполне
выполнима. В данном случае нас интересуют не математические проблемы, связанные с вычислением
подобных сумм, а физический смысл получаемых результатов.
Применим формулы (2)-(3) к расчету энергии
поля, создаваемого двумя точечными зарядами. По
принципу
суперпозиции
напряженность
электрического поля в произвольной точке,
окруженной
объемом
∆Vk
равна
сумме
напряженностей полей, создаваемых каждым зарядом
в отдельности (рис. 223)
r
r
r
E k = E1k + E 2 k .
Полную энергию поля запишем в виде1
r 2
ε0 r
W =
wk ∆Vk =
E1k + E 2 k ∆Vk =
2
k
k
.
ε0 r 2
ε0 r 2
ε0 r r
=
E1k ∆Vk +
E 2 k ∆Vk + 2
E1k ⋅ E 2 k ∆Vk
2
2
2
k
k
k
∑
∑
∑ (
∑
)
∑
(4)
Прежде всего, обратим внимание, что для энергии поля принцип суперпозиции
не выполняется – энергия системы зарядов не равна сумме энергий зарядов, взятых
по отдельности. Математическим выражением нарушения принципа суперпозиции
является нелинейная зависимость энергии от напряженности поля – плотность энергии
пропорциональна квадрату напряженности. Если напряженность поля увеличится в два
раза, то плотность энергии увеличивается в четыре раза! Кстати, аналогичное заключение
можно сделать и для полученной ранее энергии заряженной сферы – энергия
пропорциональная квадрату заряда.
Первое слагаемое в формуле (4)
ε0 r 2
W1 =
E1k ∆Vk
2
k
∑
полностью определяется зарядом q1 и не зависит от наличия второго заряда – это
слагаемое описывает энергию поля, создаваемого этим зарядом. Аналогично, второе
слагаемое
ε0 r 2
W2 =
E 2 k ∆Vk
2
k
∑
описывает энергию поля, создаваемого зарядом q 2 . Наконец третье слагаемое
ε0 r r
Wвз. = 2
E1k ⋅ E 2 k ∆Vk ,
2
k
∑
зависит от величин зарядов и от взаимного расположения. Аккуратное вычисление этой
суммы приводит к результату2
1
2
Квадрат вектора следует понимать как скалярное произведение вектора на себя.
Поверьте на слово, если не можете проверить.
151
∑
Wвз. = 2
k
ε0 r
r
qq
E1k ⋅ E 2 k ∆Vk = 1 2 = U .
2
4πε 0 r
Таким образом, это слагаемое определяет энергию взаимодействия зарядов, которая
является частью энергии электрического поля.
Если сами заряды не изменяются, то первые два слагаемых в энергии поля (4) не
изменяются при изменении взаимного расположения зарядов, поэтому их можно не
учитывать. Вспомните – протекание всех физических процессов определяется изменением
энергии, поэтому постоянная, не изменяющаяся часть энергии для описания этих
процессов не существенна.
Мы показали, что энергия заряженной сферы обратно пропорциональна ее радиусу. Точечный заряд
можно рассматривать как заряженную сферу бесконечно малого радиуса. При стремлении радиуса сферы к
нулю (при сохранении ее заряда) энергия поля стремится к бесконечности - энергия поля точечного заряда
бесконечно велика. Конечно, можно утверждать, что точечный заряд является математической абстракцией.
Однако, до настоящего времени не известно никаких экспериментальных данных о том, что электрон имеет
конечные размеры, поэтому должен рассматриваться как реально существующий точечный заряд. Эта
серьезная проблема современной физики еще ждет своего разрешения.
Аналогичным образом можно рассмотреть энергию поля, создаваемого несколькими
точечными зарядами q1 , q 2 , q3 ... Энергия поля, рассчитанная с помощью принципа
суперпозиции и формулы (3), представляется в виде
r
r
2
ε0 r
W =
wk ∆Vk =
E1k + E 2 k + E3k + ... ∆Vk =
2
k
k
ε0 r 2
ε0 r 2
ε0 r 2
=
E1k ∆Vk +
E 2 k ∆Vk +
E3k ∆Vk + ...
2
2
2
.
(4)
k
k
k
r
ε0 r r
ε0 r r
ε0 r
+2
E1k ⋅ E 2 k ∆Vk + 2
E1k ⋅ E3k ∆Vk + ... + 2
E 2 k ⋅ E3k ∆Vk + ... =
2
2
2
k
k
k
∑
∑
∑
∑ (
∑
)
∑
∑
∑
= W1 + W2 + W3 + ... + U 12 + U 13 + ... + U 23 + ...
То есть энергия этого поля является суммой энергий полей отдельных зарядов и энергий
всех парных взаимодействий.
Интересно отметить, что если бы плотность энергии зависела от напряженности не квадратично, а
по более сложному закону, то в полной энергии появились бы слагаемые, учитывающие тройные и другие
взаимодействия.
Таким образом, формулы (2)- (3) описывают полную энергию электрического поля, а
формула (1) только ее часть – энергию взаимодействия, изменяющуюся при измени
взаимного расположения зарядов.
Наконец, обсудим еще один парадокс, связанный с расчетами энергии
электрического поля. При расчете энергии взаимодействия зарядов, распределенных по
поверхности сферы, нами получен следующий результат
Q2
U=
.
8πε 0 R
Расчет полной энергии электрического поля равномерно заряженной сферы приводит к
тому же результату! Таким образом, кажется, что собственная энергия зарядов
«исчезает». Покажем, что это противоречие возникло при разбиении заряда на
Q
бесконечно малые части. Если исходный заряд разбит на N частей, величиной δQ =
N
каждый, то энергия взаимодействия эти зарядов между собой пропорциональна квадрату
1
2
заряда (δQ )
и числу взаимодействующих пар
N ( N − 1) . Таким образом
2
2
⎛Q⎞
2
U ∝ (δQ ) N ( N − 1) = ⎜ ⎟ N ( N − 1) , а при N → ∞ U ∝ Q 2 , то есть энергия
⎝N⎠
152
взаимодействия не зависит от числа частей, на который мы мысленно разбиваем
2
исходный заряд. Собственная энергия зарядов пропорциональна квадрату заряда (δQ ) и
их числу N , поэтому при N → ∞
собственная энергия стремится к нулю:
2
2
Q
⎛Q⎞
Wсоб . ∝ N (δQ ) = N ⎜ ⎟ =
→ 0 . Строго говоря,
предельный переход δQ → 0
N
⎝N⎠
физически некорректен, так электрический заряд дискретен – существует минимальный
электрический заряд. Тем не менее, учитывая малость элементарного заряда, наши
расчеты обеспечивают достаточную точность.
1
Кстати, при расчете энергии заряженной сферы мы также пренебрегли слагаемым пропорциональным
.
N
2
Для того, чтобы учесть дискретность заряда (то есть, заряжать сферу по одному электрону), следует
положить
N=
Q
, где e - элементарный заряд.
e
153
§ 10. Проводники и диэлектрики в электростатическом поле.
При известном распределении всех зарядов
расчет всех характеристик
электростатического поля представляет собой чисто техническую проблему, связанную в
общем случае только с множеством математических преобразований.
r r
Формально, электрическое поле E (r ) однозначно и напрямую посредством ряда
r r
r
r
математических операций выражается через распределение зарядов q (r ) : E (r ) = F [q(r )] .
К сожалению, точное расположение зарядов известно далеко не всегда. Во многом
это связано с тем, что электростатическое поле способно изменять распределение зарядов
в материальных телах, под действием поля могут возникать1 новые электрические заряды,
поэтому распределение электрических зарядов зависит от структуры электрического поля,
r r
r
что формально можно выразить соотношением q(r ) = G E (r ) , причем вид этой
зависимости зависит и от электрических свойств вещества, взаимодействующего с полем.
Взаимодействие электрического поля и вещества носит взаимный характер:
электрическое поле изменяет распределение зарядов в веществе, которое в свою очередь
изменяет электрическое поле. Формальные соотношения между структурой поля и
распределением зарядов имеют
вид
r r«зацикленный»
r r
r
E (r ) = F [q (r )] = F G E (r ) , или
,
r r
r
r
q (r ) = G E (r ) = G[F [q (r )]]
r r r
где функции q(r ), E (r ) заранее неизвестны. Разрешить эти уравнения удается далеко не
всегда. Поэтому для описания взаимодействия электрического поля с веществом
разработаны особые методы, введены специальные физические величины,
характеризующие это взаимодействие.
[ ]
[ ]
[ [ ]]
Особенно сложна эта проблема в случае изменяющихся во времени полях, поэтому ее изучение
начнем с рассмотрения статического взаимодействия, когда установилось равновесие между зарядами и
полем. Чтобы показать, на сколько мы упрощаем себе задачу, приведем такую аналогию: попробуйте
описать процесс наливания жидкости в стакан (струи, волны, брызги …), а в состоянии равновесия все
предельно просто – покоящаяся жидкость заполняет часть стакана, причем ее свободная поверхность
горизонтальна. Этой проблеме, описанию состояния неподвижной «электрической жидкости» внутри
неподвижных материальных тел, посвящен данный параграф. Во многом мы будем использовать
математический аппарат, рассмотренный нами при описании равновесия жидкостей, поэтому перед
изучением данного параграфа полезно повторить гидростатику – условия равновесия обычных жидкостей,
описание «электрической жидкости» во многом аналогично.
19.1 Проводники.
Строения вещества и его многообразные физические свойства мы будем изучать в
дальнейшем. Тем не менее, уже сейчас нам необходимы некоторые начальные сведения из
этой области физики.
Все различные вещества состоят из молекул и атомов, которые в свою очередь,
состоят из заряженных частиц – положительно заряженных ядер и движущихся вокруг
них отрицательно заряженных электронов. Поэтому все вещества взаимодействую с
электрическим полем. Электрические свойства различных веществ различаются весьма
заметно. Тем не менее, все вещества по своим электрическим свойствам можно разделить
на две большие группы – проводники и диэлектрики.
Проводниками называются вещества способные проводить электрический
ток. Для того, что бы вещество являлось проводником, оно должно содержать заряженные
частицы, способные достаточно свободно передвигаться по объему проводника.
Типичным представителем проводников являются металлы. Внутренняя структура
металлов, представляет собой кристаллическую решетку, образованную положительно
заряженными ионами. Электроны атомов металлов, находящиеся на высоких орбиталях,
1
Конечно, в любом случае закон сохранения электрического заряда остается незыблемым.
154
слабо связаны с ядром, при образовании кристалла отрываются от своего атома и могут
свободно передвигаться по объему всего кристалла, образуя своеобразное облако
свободных электронов. Суммарный электрический заряд проводника остается равным
нулю, электрическое поле облака свободных электронов компенсируется полем
положительных ионов кристаллической решетки. Наличие этих свободных электронов
обуславливает проводящие свойства металлов.
Подчеркнем, что свободные электроны связаны с кристаллической
решеткой, поэтому для того, чтобы покинуть металл электроны должны
получить довольно значительную дополнительную энергию. Поведение
электрона подобно поведению шарика в глубокой яме с плоским дном:
двигаться по дну может свободно, а выскочить наружу трудно (рис. 224).
Проводниками также являются растворы солей, кислот,
щелочей. При попадании этих молекул в жидкую среду они распадаются (диссоциируют)
на ионы, способные перемещаться по объему раствора и тем самым проводить
электрический ток.
При некоторых условиях проводить электрический ток могут и газы.
19.2 Условия равновесия между зарядами и электрическим полем.
r
При помещении металла2 в электрическое поле E 0 на
свободные электроны действуют электрические силы, под
действием которых электроны приходят в движение. Если
электрическое поле не слишком велико, то электроны не могут
покинуть объем металла и скапливаются на одной стороне
проводника, с другой стороны проводника образуется недостаток
электронов, поэтому положительный заряд ионов решетки
оказывается нескомпенсированным (рис. 225). Таким образом, на
поверхности проводника появляются электрические заряды, при
этом суммарный заряд проводника остается, конечно, неизменным.
Явление возникновения электрических зарядов на проводнике под
воздействием электрического поля называется электростатической индукцией, а
возникшие заряды – индуцированными.
Появившиеся индуцированные заряды создают собственное
r
индуцированное электрическое поле E ′ , которое направлено в сторону,
противоположную внешнему полю (рис. 226). Конечно, эти заряды
создают поле как внутри проводника, так и вне его. Суммарное поле
r r
r
E = E 0 + E ′ отличается от внешнего поля.
Рассмотренные особенности поведение проводников
достаточно легко проиллюстрировать экспериментально.
Мы уже упоминали, что стрелка электроскопа отклоняется
даже в том случае, когда заряженное тело не прикасается к его
стержню (рис. 227). Это явление легко объясняется явлением
электростатической индукции. Для увеличения эффекта, на
стержень электроскопа следует насадить сферическую насадку.
Поднесем к металлической сфере заряженную стеклянную
палочку, заряд которой
положительный. Под действием
электрического
поля
зарядов
палочки
произойдет
перераспределение зарядов на сферической насадке, стержне и
стрелке. Отрицательно заряженные электроны под действием
электрического поля будут приближаться к палочке, поэтому
сфера приобретет отрицательный заряд, равный ему положительный заряд распределится
2
В данном разделе мы говорить главным образом о поведении металлов в электрическом поле, хотя
аналогичные явления происходят и в других типах проводников.
155
между стержнем и стрелкой. Суммарный заряд электроскопа останется равным нулю.
Вследствие электрического отталкивания между положительными зарядами стержня и
стрелки, последняя отклонится.
Зарядим электроскоп, прикоснувшись к нему
заряженной стеклянной палочкой. Если
теперь
к
насадке поднести незаряженное проводящее тело
(например, просто свою руку), не касаясь насадки,
отклонение стрелки электроскопа уменьшится (рис.
228). Это явление объясняется следующим образом:
под действием положительного заряда электроскопа на
руке индуцируются заряды противоположного знака,
которые притянут положительные заряды стрелки и
стержня к насадке, то есть между ними произойдет
перераспределение зарядов, в результате чего заряд
стрелки и стержня уменьшится.
Электростатической индукцией объясняется и
притяжение незаряженного тела к заряженному. Если заряженную стеклянную палочку
поднести к небольшому проводящему телу (например, кусочку фольги), то в этом теле
произойдет перераспределение зарядов: ближняя к
палочке часть зарядится отрицательно, дальняя
положительно (рис. 229). Следовательно, тело
приобретет дипольный момент. Так как электрическое
поле, создаваемое зарядом палочки не является
однородным, а убывает с расстоянием, то на кусочек фольги будет действовать сила
притяжения, поэтому незаряженное тело втягивается в
область более сильного поля.
Подчеркнем, одним из необходимых условий
притяжения незаряженного тела к заряженному является
неоднородность электрического поля – если поместить
проводящее тело в однородное электрическое поле (рис.
230), то индуцированные заряды возникнут, но суммарная
сила, действующая на них, будет равна нулю!
Задание для самостоятельной работы.
1. Что произойдет с отклонением стрелки заряженного электроскопа, если к его насадке
поднести другое заряженное тело (не касаясь насадки)?
Некоторые важнейшие свойства электрического поля, и распределения зарядов на
проводниках можно получить, рассматривая только условия равновесия электрических
зарядов. Условия равновесия не изменятся, если проводнику сообщить избыточный заряд,
который также перераспределится по поверхности проводника, и также будет создавать
электрическое поле. Далее, мы рассмотрим условия равновесия зарядов на проводнике и
электрического поля, независимо от того, какими зарядами это поле создается –
изначально находящимися на проводнике, индуцированными, или внешними; тем более,
что нет принципиальной возможности разделить и различить эти поля, так как
единственной реальностью является суммарное электрическое поле.
r r
1. Напряженность электрического поля внутри проводника равна нулю E = 0 .
Можно предположить, что заряды, возникающие на поверхности проводника,
образуются крайне незначительной долей общего количества свободных электронов,
поэтому внутри проводника всегда имеется значительное число свободных электронов.
Если внутри проводника существует отличное от нуля электрическое поле, то под его
действием свободные электроны будут продолжать перемещаться, в стационарном же
156
состоянии равновесия такое движение прекращается. Следовательно, в состоянии
r
r
равновесия поле индуцированных зарядов E ′ полностью компенсирует внешнее поле E 0 .
В некоторых пособиях утверждается, что проводники «не пропускают» электрическое поле. Данное
высказывание не совсем корректно – проводник создает собственное поле, которое компенсирует внешнее,
породившее его поле.
Проверим высказанное предположение о малости числа
электронов, образующих индуцированные заряды. Пусть медная
пластинка помещена в однородное электрическое поле
перпендикулярно его силовым линиям (рис. 231).
Под действием внешнего электрического поля на гранях
пластинки возникнут индуцированные электрические заряды,
поверхностную плотность которых обозначим σ . Эти заряды
породят электрическое поле, напряженность которого равна E ′ =
σ
. В состоянии
ε0
r
равновесия это поле полностью компенсирует внешнее поле E 0 , поэтому E ′ = E 0 , а
поверхностная плотность индуцированных зарядов связана с напряженностью внешнего
поля соотношением σ = ε 0 E 0 . Число электронов, приходящихся на единицу площади
σ ε E
поверхности (поверхностная концентрация), равно n пов . = = 0 0 , где e - заряд
e
e
электрона. Для численной оценки примем, что напряженность внешнего поля равна
В
В
E 0 = 1 ⋅ 10 5 = 1 ⋅ 10 3
(что в тысячу раз превышает напряженность электрического поля
м
см
Земли). Тогда поверхностная концентрация электронов равна
ε E
8,85 ⋅ 10 −12 ⋅ 1 ⋅ 10 5
n пов. = 0 0 =
≈ 6 ⋅ 1012 м − 2 = 6 ⋅ 1010 см − 2 .
−19
e
1,6 ⋅ 10
На первый взгляд достаточно много, но сравним с общим числом электронов в единице
объема. Для расчета концентрации электронов примем, что каждый атом меди отдает
один электрон в электронное облако. Число атомов меди (следовательно, и число
свободных электронов) в единице объема рассчитаем следующим образом: масса единицы
г
объема равна плотности меди ρ ≈ 9 3 ; число молей вещества в единице объема равно
см
m
г
ρ
- молярная масса меди; концентрация атомов3 (и свободных
ν=
=
, где M ≈ 65
M M
моль
г
9 3
ρ
см ⋅ 6 ⋅ 10 23 моль −1 ≈ 8 ⋅ 10 22 см −3 .
электронов) nоб . = νN A =
NA =
г
M
65
моль
Если принять толщину пластинки h = 1 см , то доля электронов, которые оказались на
n
поверхности, оказывается равной η = пов. ≈ 10 −12 , что действительно крайне мало (одна
nоб . h
десятимиллиардная доля процента).
Напомним, такая доля электронов создает индуцированные заряды, если к медной
пластинке толщиной в один сантиметр приложить напряжение в тысячу вольт! Поэтому с
высокой степенью точности можно считать, что появление индуцированных зарядов не
изменяет объемную концентрацию свободных электронов.
3
Здесь N A = 6,02 ⋅ 10 23 моль −1 - число Авогадро.
157
2. Все точки проводника имеют одинаковые потенциалы.
Это утверждение является прямым следствием связи между разностью потенциалов и
r r
напряженностью поля ∆ϕ = − E ⋅ ∆l . Если напряженность поля внутри проводника равна
нулю, то разность потенциалов также равна нулю, поэтому потенциалы всех точек
проводника одинаковы. Также можно привести еще одно равноценное доказательство:
если между двумя точками проводника существует разность потенциалов, то между ними
будет течь электрический ток, то есть равновесия не будет.
3. В состоянии равновесия все заряды располагаются только на поверхности проводника,
объемная плотность электрического заряда внутри проводника равна нулю.
Доказательство этого утверждения проведем методом от
противного. Допустим, что в некоторой части проводника
существует заряженная область. Окружим эту область замкнутой
поверхностью S (рис. 232). Согласно теореме Гаусса поток вектора
напряженности электрического поля через эту поверхность отличен
от нуля и пропорционален заряду, находящемуся внутри
поверхности. Следовательно, в точках этой поверхности
напряженность электрического поля отлична от нуля. Но мы
доказали, что в состоянии равновесия внутри проводника электрическое поле отсутствует,
мы пришли к противоречию, поэтому внутри проводника электрические заряды
отсутствуют. Реально, если каким то образом внутрь проводника поместить избыточный
электрический заряд, то под действием сил отталкивания этот заряд «разбежится» на
поверхность проводника.
Строго говоря, электрические заряды существуют в очень тонком слое вблизи поверхности,
толщина которого измеряется несколькими атомными слоями, поэтому практически можно говорить о
поверхностном заряде, пренебрегая толщиной заряженного слоя.
4. У поверхности проводника вектор напряженности электрического поля направлен
перпендикулярно поверхности проводника.
Опять воспользуемся доказательством методом от
противного – предположим, что в некоторой точке поверхности
r
проводника вектор напряженности электрического поля E
направлен под некоторым углом к поверхности проводника
(рис. 233). Разложим это вектор на две составляющих:
r
En ,
перпендикулярную
поверхности,
и
нормальную
r
тангенциальную Eτ - направленную по касательной к
поверхности. Аналогично можно провести и разложения
вектора силы, действующей на электроны. Нормальная составляющая этой электрической
силы уравновешивается силой, действующей на электрон со стороны кристаллической
решетки. Под действием же тангенциальной составляющей электроны придут в движение
вдоль поверхности, но …нас интересует состояние равновесия, поэтому в состоянии
равновесия тангенциальная составляющая электрического поля отсутствует.
Если в какой-то момент времени тангенциальная составляющая поля отлична от нуля, то
под ее действием начнется движение электрических зарядов, которое будет продолжаться
до тех пор, пока не установится такое распределение зарядов, при котором вектор поля
будет перпендикулярен поверхности во всех ее точках.
связана с
5. Напряженность электрического поля у поверхности проводника
поверхностной плотностью зарядов соотношением E =
σ
.
ε0
Итак, мы установили, что внутри проводника напряженность электрического поля
равна нулю, а у поверхности вектор напряженности перпендикулярен поверхности
проводника. Кроме того, электрические заряды локализованы на поверхности проводника.
158
Эти факты позволяют с помощью теоремы Гаусса установить связь между
напряженностью поля и поверхностной плотностью заряда.
Выделим на поверхности проводника малую
∆S ,
поверхностную
площадку,
площадью
плотность заряда на ней обозначим σ , и будем
считать ее постоянной в пределах выбранной малой
площадки (рис. 234). Окружим эту площадку
замкнутой поверхностью, состоящей из двух
частей: первая Ω1 расположена над поверхностью и
непосредственно примыкает к выбранной площадке
∆S , вторая Ω 2 находится под поверхностью, внутри проводника. Поток вектора
напряженности через поверхность Ω 2 равен нулю, так как внутри проводника поля
отсутствует Φ E 2 = 0 ; поток вектора напряженности через поверхность Ω1 равен
произведению напряженности поля на площадь площадки Φ E1 = E∆S , так как на этой
поверхности вектор напряженности направлен вдоль нормали. Так как Ω1 и Ω 2 образуют
замкнутую поверхность, то суммарный поток через нее равен заряду, находящемуся
внутри поверхности
q = σ∆S , деленному на электрическую постоянную ε 0 :
q
σ∆S
Φ E1 + Φ E 2 = . Подставив выражения для потоков и заряда E∆S + 0 =
, получим
ε0
ε0
искомое соотношение
E=
σ
.
ε0
(1)
К сожалению, эта формула только устанавливает связь между напряженностью поля и
плотностью заряда, хотя обе величины остаются неизвестными.
Следует отметить, что электрическое поле E , входящее в
формулу (1) создается не только зарядами, находящимися на
выбранной площадке4 ∆S , но и всеми остальными зарядами на
проводнике и вне его (рис. 235). Представим это поле в виде суммы
r r
r
r
полей E = E 0 + E1 , где E 0 напряженность поля, создаваемого
r
зарядами на площадке σ 0 ; E1 - напряженность поля, создаваемого
всеми остальными зарядами σ 1 . Рассмотрим теперь эти поля
непосредственно под площадкой ∆S внутри проводника.
r
Напряженность поля E 0′ зарядов σ 0 будет направлена в противоположную сторону, так
как рассматривается точка с противоположной стороны площадки. А напряженность поля
остальных зарядов остается неизменной, так как мы выбираем две точки в
непосредственной близости друг от друга. Теперь, внимание, так как внутри проводника
r
r
r
поле отсутствует, то E1 − E 0 = 0 , поэтому модули напряженности этих полей равны и
σ
E
. С помощью полученного соотношения
определяются формулой E 0 = E1 = =
2 2ε 0
можно вычислить силу, действующую на выбранную площадку поверхности, как
произведение заряда площадки q = σ∆S = ε 0 E∆S на напряженность поля E1 , создаваемого
всеми зарядами кроме, заряда на самой площадке F = qE1 =
ε0E2
2
∆S . Сила, действующая
4
Напомним, поток вектора напряженности через замкнутую поверхность полностью определяется зарядами
внутри поверхности, то есть в данном случае зарядами на поверхности.
159
на единицу площади поверхности проводника со стороны электрического поля (то есть
давление поля) вычисляется по формуле
ε0E2
F
P=
=
.
2
∆S
Удивитесь (и попытайтесь его осмыслить) полученному результату: давление электростатического поля на
поверхность проводника равно плотности энергии электрического поля!
19.3 Применение электростатических свойств проводников.
Приведем некоторые примеры использования рассмотренных свойств поведения
проводников в электрическом поле.
Электростатическая защита.
Иногда возникает необходимость изолировать некоторые тела, приборы от
воздействия внешних электрических полей. Для такой изоляции их помещают внутрь
металлического корпуса. Мы показали, что при помещении проводника во внешнее
электрическое поле, индуцированные заряды возникают только на поверхности
проводника, а поле внутри проводника оказывается равным нулю.
Пусть, например, металлический шар помещен в однородное электрическое поле
r
напряженностью E 0 (рис. 236). Под действием этого поля на поверхности шара возникнут
индуцированные заряды, поверхностная плотность которых σ 0 , будет различна в
различных точках поверхности шара. Эти заряды приведут к изменению электрического
поля: внутри шара напряженность поля станет равной нулю, снаружи – силовые линии
поля будут перпендикулярны поверхности шара. Если теперь внутри шара вырезать
произвольную полость, то от этой «операции» распределение поля и индуцированных
зарядов не изменится, так как изъята та часть шара, где нет ни зарядов, ни поля.
Аналогичные рассуждения можно распространить на произвольную полость внутри
проводящего тела произвольной формы,
находящегося в произвольном
электростатическом поле – в любом случае поле внутри полости будет отсутствовать.
Говорят, что проводящая оболочка экранирует внешнее электрическое поле.
Более того, можно показать, что аналогичного эффекта достигается даже в том
случае, если сплошную проводящую оболочку заменить на металлическую сетку с
мелкими ячейками. В этом случае электрическое поле проникает за сетку на глубину
порядка размеров ячейки сетки.
Подчеркнем, что сплошная металлическая оболочка экранирует электрическое
поле, находящееся снаружи от оболочки, но не те, которые находятся внутри нее. Пусть
точечный заряд + q0 находится внутри металлической сферической оболочки (рис. 237).
Этот заряд создает электрическое поле, которое индуцирует электрические заряды, как на
160
внутренней, так и на внешней поверхностях оболочки. Рассмотрим, как в этом случае
изменится распределение электрического поля.
На
внутренней
поверхности
распределятся
отрицательные
заряды
с
некоторой поверхностной плотностью σ 1 .
Внутри металла напряженность поля равна
нулю, поэтому отрицательные индуцированные
заряды σ 1 полностью экранируют поля заряда
q0 . Используя теорему Гаусса, легко показать,
что суммарный заряд, индуцированный на
внутренней
поверхности,
равен
− q0 .
Суммарный заряд оболочки остается равным
нулю,
следовательно,
на
ее
внешней
поверхности индуцируется положительный
заряд равный
+ q0 . На поверхностное
распределение этого заряда σ 2 , заряды
внутренней поверхности и заряд полости не действуют, поэтому они распределятся по
поверхности оболочки равномерно, и вне оболочки будут создавать электрическое поле
эквивалентное полю точечного заряда + q0 , помещенного в центр сферической оболочки.
Подчеркнем такое распределение поля вне оболочки не зависит от положения заряда
внутри полости – смещение этого заряда приведет к изменению поля внутри полости,
изменению распределения зарядов на внутренней поверхности, но не изменяет поля вне
оболочки.
Чтобы «убрать» поле снаружи от оболочки ей необходимо сообщить дополнительный
отрицательный заряд, такого эффекта можно добиться, заземлив оболочку.
Заземление.
Как распределяются заряды между двумя связанными проводящими телами?
С точки зрения здравого смысла на теле больших
размеров
должен
накапливаться
больший
электрический заряд. Чтобы обосновать это
утверждение, рассмотрим два проводящих шара,
радиусы которых обозначим R1 , R2 , находящиеся на
большом расстоянии l друг от друга ( l >> R1 , R2 ), и
соединенных проводником (рис. 238). Если этой
системе сообщить электрический заряд Q , то заряды
шаров q1 , q 2 распределятся так, чтобы их потенциалы
были равны; суммарный же заряд системы, конечно,
останется равным сообщенному заряду q1 + q 2 = Q . Так как расстояние между шарами
значительно больше их радиусов, то при расчете потенциала каждого шара можно
пренебречь их взаимным влиянием и воспользоваться формулой для потенциала
уединенного шара
q1
q2
.
ϕ1 =
, ϕ2 =
4πε 0 R1
4πε 0 R2
Приравнивая эти потенциалы, получим, что заряды шаров пропорциональны их радиусам
q1 R1
,
=
q 2 R2
или
161
R2
R1
Q.
(1)
Q, q 2 =
R1 + R2
R1 + R2
Качественно аналогичный вывод справедлив и для проводящих тел произвольной
формы. Если одно из тел значительно больше другого, то практически весь заряд
окажется на большем теле. Действительно, из формул (1) следует, что при R2 >> R1
q1 ≈ 0 , q 2 ≈ Q .
(2)
Именно это обстоятельство используется для того, чтобы разрядить небольшое
заряженное тело – его необходимо соединить с телом больших размеров. Так если к
заряженному электроскопу прикоснуться рукой, то заряд перераспределится между
электроскопом и телом человека, но так как размер последнего значительно больше
размеров электроскопа, то можно считать, что весь заряд «сбежит» на человека. Часто в
качестве тела больших размеров используют весь земной шар. Приборы, на которых не
должен собираться электрический заряд «заземляют», для чего подключают их к
массивному проводнику, закопанному в землю. В этом случае можно считать, что
соотношения (2) выполняются точно. На схемах для указания того, что тело или прибор
q1 =
заземлены, используется специальное обозначение .
В теоретических расчетах полагают, что заземление – есть соединение данного
тела с телом бесконечно больших размеров, так что потенциал этого тела не изменяется
при сообщении ему произвольного заряда и, наоборот, при необходимости это тело может
сообщить произвольный заряд, не изменяя его потенциала, который естественно можно
положить равным нулю. Поэтому также можно сказать, что заземление – это «соединение
с бесконечностью», а потенциал заземленного тела равен нулю, кроме того, суммарный
заряд заземленного тела может изменяться.
Уместно привести следующую аналогию. Если небольшое тело находится в тепловом контакте с
окружающей средой, то с течением времени его температура станет равной температуре окружающей
среды, независимо от того, было тело первоначально нагрето или охлаждено. То есть окружающая среда
может получить любое количество теплоты, или отдать любое количество теплоты, а при этом ее
температура не изменяется. Такая модель окружающей среды называется термостатом. Заземление в
электростатике играет такую же роль, как окружающая среда (термостат) в теории тепловых явлений.
Если рассмотренную в предыдущем разделе сферическую оболочку заземлить, то
положительные заряды на внешней поверхности «исчезнут –
уйдут в землю», поэтому поле вне оболочки также исчезнет
(рис. 239). Можно рассуждать и в обратном порядке: если
внутрь полости заземленной оболочки поместить электрический
заряд, то его поле индуцирует заряды противоположного знака
на внутренней поверхности, эти заряды «прибегут из
заземления».
Заметим, что поле внутри заземленной полости
полностью определяется ее формой и распределением зарядов
внутри нее и не зависит от формы всего тела и заряда
последнего.
162
Генератор Ван-дер-Граафа.
Как мы показали, в условиях равновесия электрический заряд распределяется по
внешней поверхности проводника – это позволяет в некоторых случаях накапливать на
проводниках значительные электрические заряды.
Можно провести следующий эксперимент. На
изолирующей
ручке
расположен
небольшой
металлический шарик (рис. 240). Если этому шарику
сообщить небольшой электрический заряд q0 (например, с
помощью стеклянной палочки) и прикоснуться шариком к
поверхности сферической насадки электроскопа, то
только часть этого заряда перейдет на электроскоп. Если
затем опять зарядить шарик до прежнего значения заряда
q0 и опять прикоснуться к внешней поверхности насадки,
то меньшая часть заряда шарика перейдет на электроскоп.
Таким способом можно сообщить электроскопу только
конечный заряд, сколько бы раз мы не подзаряжали
шарик. Действительно, когда потенциалы уединенного
шарика и электроскопа сравняются, то перераспределение зарядов прекратится.
Приближенно максимальный заряд электроскопа Qmax при таком способе зарядки можно
R
оценить из условия равенства потенциалов, поэтому Qmax ≈ q 0 , где R - радиус насадки
r
электроскопа, r - радиус шарика. Если же зарядку электроскопа проводить с помощью
такого же шарика, но прикасаясь к внутренней поверхности насадки, то электроскопу
можно сообщить гораздо больший заряд. Действительно, если прикоснуться шариком к
внутренней поверхности, то весь его заряд перейдет на внешнюю поверхность насадки,
независимо от того, какой заряд на ней находится. В этом случае максимальный заряд
электроскопа будет определяться внешними причинами – при очень большом заряде
насадке начнется утечка зарядов через окружающую среду, т.е. через воздух.
По этому принципу работают устройства, позволяющие накапливать очень
большие заряды (соответственно создающие большие
разности потенциалов). Одним из первых таких
устройств (заметим, использующихся до настоящего
времени) является электростатический генератор Вандер-Граафа, принципиальная схема которого показана на
рисунке 241. В генераторе Ван-дер-Граафа резиновая
лента приводится в движение с небольшой скоростью
электродвигателем. При движении лента проходит
между
электрически
заряженными
пластинами.
Возникшие на ленте индуцированные заряды снимаются
с внешней поверхности ленты с помощью контактной
щетки и подаются на внутреннюю поверхность
металлическом купола генератора, создавая достаточно
сильные электростатические поля (высокие напряжения)
в окружающем купол пространстве. Заряды с внутренней
стороны ленты отводятся через шину заземления.
Максимальный электрический заряд купола (и его
потенциал) ограничиваются только утечкой заряда с
купола через воздух. Такие генераторы используются для создания высокой разности
потенциалов в линейных ускорителях частиц. Диаметр купола генератора может
составлять несколько метров, а создаваемая разность потенциалов несколько миллионов
вольт.
163
10.4 Расчет поля в присутствии проводников. Метод изображений.
Мы уже подчеркивали, что основная проблема расчета полей в присутствии
проводников заключается в появлении индуцированных зарядов, распределение которых
заранее не известно. В связи с этим рассмотренные ранее методы, основанные на законе
Кулона и принципе суперпозиции, в данном случае оказываются непригодными.
Принципиально иной подход
к решению данной задачи заключается в расчете
распределения потенциала электростатического поля. Действительно, на поверхности
проводника распределение заряда не известно, но ведь потенциал проводника постоянен!
Сам метод основан на решении уравнений1 для потенциала поля. Сами эти
уравнения довольно сложны и рассматриваются в курсе физики высшей школы, однако,
их физический смысл основывается на законе Кулона и связи потенциала с
напряженностью поля.
Однако в некоторых случаях можно рассчитать электрическое поле и
распределение индуцированных на поверхности проводника зарядов, используя
искусственный прием, который называется метод изображений.
Изложим кратко суть и дадим обоснование этого метода.
Пусть в некоторой области пространства V , ограниченной
поверхностью S (в частном случае граница области может
простираться до бесконечности), задано распределение зарядов qi
(рис. 242).
Электрическое поле в выделенной области определяется
однозначно, если
- задано распределение зарядов внутри этой области;
- задано распределение потенциала на границе области.
Заметим, что на границе области могут существовать заряды, однако даже при
неизвестном их распределении, задание потенциала на границе однозначно определяет
поле внутри области. Поэтому две различные задачи, но с одинаковыми распределениями
зарядов внутри области и одинаковыми потенциалами на границе имеют внутри области
одинаковые решения. Иногда при неизвестном распределении индуцированных зарядов
на границе удается подобрать такое распределение зарядов вне рассматриваемой области,
что для нового распределения выполненяются граничные условия исходной задачи. В
этом случае дополнительные заряды называются зарядами-изображениями. Поиск
изображений имеет смысл вести тогда, когда новая задача оказывается проще исходной и
имеет простое решение.
Помимо задания распределения потенциала, в качестве граничных условий могут использоваться и
некоторые другие, например, значение напряженности поля. Формулировке граничных условий, по этой
причине уделяется серьезное внимание в курсе электродинамики.
Точечный заряд над плоской проводящей поверхностью.
Рассмотрим простейшую задачу, допускающую
решение с помощью метода изображений.
Пусть точечный заряд + q 0 находится на расстоянии l
от бесконечной металлической пластины (рис. 243).
Очередной раз мы пользуемся моделями – в данном случае под
бесконечной, понимается пластина, размеры которой значительно
больше расстояния до заряда. Кроме того, можно считать, что пластина
заземлена, так как она «касается бесконечности».
Под действием электрического поля заряда + q 0 электроны пластины придут в
движения и начнут скапливаться под точечным зарядом, создавая отрицательный
индуцированный заряд.
1
Эти уравнения называются уравнениями С. Пуассона, или в частных случаях уравнениями П. Лапласа. С
математической точки зрения они являются уравнениями в частных производных, поэтому их изучение
далеко выходит за рамки наших возможностей.
164
Если пластина реально заземлена, то эти заряды натекут из заземления. На большой незаземленной
пластине возникнут положительные заряды на краях пластины, но так как эти края находятся далеко, то их
полем в рассматриваемой области можно пренебречь.
Распределение поверхностной плотности индуцированных зарядов на пластине σ
не известно, но известно, что ее потенциал постоянен и равен нулю.
Легко придумать другую задачу, для
которой будет выполнено такое же граничное
условие.
Действительно,
рассмотрим
поле,
создаваемое двумя точечными зарядами q = + q 0 и
q ′ = −q 0 , находящимися на расстоянии 2l друг от
друга (рис. 244). Во всех точках плоскости,
перпендикулярной отрезку, соединяющими заряды
и проходящей через ее середину, потенциал равен
нулю, так как эти точки находятся на равном
расстоянии от двух зарядов равных по величине и противоположных по направлению.
Сравним данную простую задачу (два точечных заряда) с исходной (точечный
заряд и индуцированные им заряды σ на проводящей пластине): в полупространстве над
пластиной распределения зарядов одинаковы (в обоих случаях – один точечный заряд), на
граничной плоскости потенциалы равны; следовательно, в этом полупространстве
электрические поля также одинаковы.
Строго говоря, мы должны рассматривать замкнутую
область пространства, поэтому мысленно накроем заряд + q 0
полусферой, опирающейся на плоскость, положим ее потенциал
равным нулю и устремим ее радиус к бесконечности, и таким
образом придем к рассматриваемому полупространству (рис. 245).
Таким образом, в верхнем полупространстве
задачи эквивалентны – заряды и поле распределены
одинаково. Следовательно, можно утверждать, что индуцированные на металлической
пластине заряды σ создают в верхнем полупространстве такое же электрическое поле как
заряд q ′ = −q0 , расположенный симметрично относительно верхней поверхности
пластины. Следовательно, для расчета электрического поля следует зеркально
симметрично под пластиной расположить заряд-изображение q ′ = −q 0 . Подчеркнем, что
реально никакого такого заряда не возникает, его роль – описать поле, создаваемое
реальными индуцированными зарядами на поверхности пластины. Ввиду явной
симметрии такое же поле возникает и в нижнем полупространстве (то есть поле заряда
q ′ , расположенного в той же точке, что и исходный заряд + q 0 ). Это поле
индуцированных зарядов складывается с полем исходного заряда, поэтому и оказывается,
что в нижнем полупространстве поле равно нулю, как и должно быть внутри проводника.
r
Напряженность суммарного поля у границы E0 можно
рассчитать по принципу суперпозиции как сумму полей,
r
r
создаваемых исходным зарядом E и его изображением E ′ (рис.
246):
r
r r
E0 = E ′ + E .
Суммарный вектор направлен перпендикулярно границе и равен
q
ql
,
E0 = 2
cos α =
2
2
3
4πε 0 (l + r )
2
2 2
2πε 0 (l + r )
здесь r расстояние от основания перпендикуляра из заряда на
плоскость пластины до рассматриваемой точки. Поверхностная плотность заряда у
поверхности проводника связана с напряженностью поля соотношением σ = ε 0 E , поэтому
165
распределение поверхностной
осесимметрично и имеет вид
плотности
σ =
индуцированных
ql
3
2
зарядов
на
пластине
.
2π (l 2 + r 2 )
Сила притяжения заряда к пластине определяется полем, создаваемым
индуцированными зарядами, которое в свою очередь эквивалентно полю заряда
изображения, поэтому равно силе взаимодействия двух точечных зарядов q и q′
q2
q2
=
−
.
4πε 0 (2l ) 2
16πε 0 l 2
Энергия взаимодействия исходного и индуцированных зарядов равна только
половине (!) энергии взаимодействия зарядов q и q′ . Заметьте, что две задачи (заряд и
пластина - два заряда) эквивалентны только в верхнем полупространстве. Реально поле
существует только в верхней половине пространства. Так энергия взаимодействия есть
энергия поля, то и энергия взаимодействия будет в два раза меньше. Поэтому
1
q2
q2
=−
.
W =− ⋅
2 4πε 0 (2l )
16πε 0 l
Этот вывод можно пояснить следующим образом: при двух реальных точечных зарядах
при перемещении одного из них второй остается неподвижным. Если же уносить заряд от
проводящей границы, то его изображение также удаляется, поэтому совершаемая работа
будет меньше.
Картина силовых линий также может быть рассчитана, как поле двух точечных
зарядов (рис. 247). Обратите внимание, что во всех точках плоскости силовые линии
перпендикулярны поверхности.
F =−
Продолжим развитие идей построения зарядов-изображений.
Пусть точечный заряд q находится на биссектрисе
прямого двугранного угла AOB , образованного двумя
бесконечными проводящими плоскостями (рис. 248).
Попытаемся построить набор зарядов изображений так, чтобы
удовлетворить граничным условиям - на гранях угла потенциал
должен быть равен нулю. Прежде всего, зеркально отобразим
исходный заряд в двух плоскостях - получим два изображения
q′ . Но эти три заряда не обеспечивают равенство нулю
потенциала на гранях угла. Необходимо еще один раз
отобразить изображения в другой грани - тем самым появляется
еще один заряд-изображение q′′ . Отметим, что этот заряд
является одновременно изображением обоих зарядов q′ . Однако его величина также
равна q (а не 2q ), так как единственное и основное правило построения - удовлетворение
граничных условий. Легко проверить, что поле четырех зарядов имеет нулевой потенциал,
166
как на плоскости OA , так и на плоскости OB . Таким образом, поле, образованное зарядом
q и индуцированными на плоскостях зарядами эквивалентно полю четырех точечных
зарядов, причем эта эквивалентность выполняется только в одной четверти угла,
содержащей исходный заряд. В оставшихся четвертях поле отсутствует. Но картина
силовых линий получается достаточно симпатичной, если построить поле четырех
зарядов, подразумевая, что реально поле только в одной четверти, поэтому в остальных
четвертях оно заштриховано (рис. 249).
Совершенно аналогично можно построить поле заряда, помещенного на
биссектрису двугранного угла, величина которого целое число раз укладывается в полном
угле, например, в угле 60° . Шесть зарядов, знаки которых чередуются, расположенных в
вершинах правильного шестиугольника, обеспечивают равенство нулю потенциала на
гранях угла.
Изображение заряда в сфере.
Прежде, чем приступить к рассмотрению следующей группы задач, связанных с
описанием взаимодействия точечного заряда и проводящей сферы, решим одну
вспомогательную задачу.
Пусть электростатическое поле создается двумя точечными зарядами,
находящимися на расстоянии l друг от друга. Величины и знаки зарядов различны и
равны q1 и − q2 . Покажем, что поверхность нулевого потенциала этого поля представляет
собой сферу.
Выберем систему координат, так чтобы
заряд q1 находился в начале координат, а заряд q 2
на оси Ox (рис. 250). Так задача обладает осевой
симметрией, то достаточно показать, что в
плоскости xOy линия нулевого потенциала
является окружностью. Запишем выражение для
потенциала
электростатического
поля
в
произвольной точке A с координатами ( x, y )
q1
q2
q1
q2
1
+
=
+
(
).
ϕ=
2
2
4πε 0 r1 4πε 0 r2 4πε 0 x + y
(x − l)2 + y 2
Полагая ϕ = 0 , получим уравнение, определяющее линию нулевого потенциала.
q2
= k , и преобразуем это уравнение к виду:
Обозначим
q1
167
k 2l 2
l
2
2
+
=
)
.
y
(k 2 − 1) 2
k2 −1
kl
А это есть уравнение окружности радиуса R = 2
с центром, лежащим на оси X в
k −1
l
точке с координатой xC = − 2
. В пространстве, с учетом осевой симметрии (вращая
k −1
вокруг оси X ) эта линии образует сферу.
Итак, запомним – в поле создаваемом двумя точечными зарядами разными по
знаку и величине, поверхность нулевого потенциала представляет собой сферу.
Рассмотрим теперь такую систему: точечный заряд q расположен на расстоянии l
от центра металлической заземленной сферы радиуса R . Исследуем электрическое поле
в этом случае.
На поверхности металлической заземленной сферы возникнут индуцированные
заряды, распределение которых заранее не известно, однако потенциал сферы равен нулю.
Мы показали, что поле двух точечных зарядов имеет в качестве поверхности нулевого
потенциала сферу. Теперь мы можем использовать этот результат.
Для этого необходимо внутри сферы можно построить заряд изображение q' ,
такой, чтобы поле двух точечных зарядов имело нулевой потенциал на поверхности
сферы. В этом случае вне сферы поле двух точечных зарядов q, q' и поле, создаваемое
зарядом q и зарядами, индуцированными на поверхности металлической сферы, будут
одинаковыми. (Вне сферы распределения зарядов одинаковы, на границе - одинаковые
граничные условия – поэтому поля вне сферы будут одинаковыми).
Для определения величины заряда-изображения q ′ и его положения можно
потребовать выполнения условия ϕ = 0 в двух
точках сферы, например, A и B (рис. 251):
1
1
q
q′
=0
+
4πε 0 l − R 4πε 0 R − x
.
1
1
q
q′
+
=0
4πε 0 l + R 4πε 0 R + x
Решив эту систему относительно неизвестных q ′
и x , получим
R
R2
q ′ = −q ; x =
.
l
l
Таким образом, вне сферы поле эквивалентно полю двух точечных зарядов
исходного q и найденного заряда изображения q ′ . Внутри сферы эти поля, конечно же,
различаются - внутри реальной проводящей сферы поле отсутствует.
Для определения суммарного индуцированного заряда воспользуемся теоремой
Гаусса. Окружим сферу замкнутой поверхностью. По теореме Гаусса, поток вектора
напряженности электрического поля через эту поверхность равен суммарному заряду
внутри поверхности, деленному на ε 0 . Так поле индуцированных зарядов эквивалентно
полю заряда изображения, то и суммарный индуцированный заряд равен величине зарядаR
изображения q ′ = − q .
l
На рисунке 252 показаны силовые линии поля, при двух различных значениях
расстояниях до точечного заряда. Обратите внимание, что при увеличении расстояния
между зарядом и сферой искажения поля точечного заряда уменьшаются. Как всегда, у
поверхности проводника силовые линии перпендикулярны границе, что соответствует
условию равновесия индуцированных зарядов на поверхности проводника.
(x +
168
Еще раз подчеркнем - вне сферы поля эквивалентны, но это не значит, что индуцированные заряды
концентрируются в одной точке - они распределены по поверхности сферы.
Силу взаимодействия между сферой и точечным зарядом можно найти как силу
взаимодействия между двумя точечными зарядами q, q ′ :
qq ′
q2
Rl
.
F=
=−
⋅ 2
2
4πε 0 (l − R 2 ) 2
4πε 0 (l − x)
Заметим, что при l >> R сила взаимодействия становится равной
q2 R
F =−
⋅ ,
4πε 0 l 3
то есть сила убывает обратно пропорционально кубу расстояния. Такая зависимость
может быть качественно объяснена: величина заряда, индуцированного на сфере обратно
пропорциональна расстоянию до исходного заряда, а сила взаимодействия между
точечными зарядами обратно пропорциональна квадрату расстояния - следовательно, сила
взаимодействия сферы и заряда обратно пропорциональна кубу расстояния.
Рассмотрим, как изменится картина поля, если сфера не заземлена. Потенциал
незаземленной сферы отличен от нуля, но по-прежнему постоянен, но величина его
заранее не известна.
Но для изолированной сферы
суммарный индуцированный заряд равен нулю - в поле
точечного заряда произойдет только перераспределение
зарядов по поверхности сферы. Мы можем добиться
выполнения граничных условий, поместив в центр шара
еще один заряд-изображение q′′ = − q′ (рис. 253).
Действительно, заряды q, q ′ создают поле, потенциал
которого на поверхности сферы равен нулю, а заряд, помещенный в центре сферы, на ее
поверхности создает постоянный (но не равный нулю) потенциал, поэтому
эквипотенциальность сферы не нарушится. Из теоремы Гаусса следует, что суммарный
индуцированный заряд сферы равен сумме зарядов изображений, поэтому при
выполнении условия q′′ = − q′ , этот заряд окажется равным нулю.
Итак, вне сферы поле, создаваемое точечным зарядом q и индуцированными
зарядами на поверхности, эквивалентно полю трех точечных зарядов q, q′, q′′ .
Обратите внимание, число зарядов изображений определяется только необходимостью выполнения
граничных условий.
169
На рисунке 254 показана картина
силовых
линий
электрического
поля
рассматриваемой системы зарядов. Обратите
внимание, что имеются силовые линии,
начинающиеся на положительных зарядах
сферы. Незаземленная сфера гораздо меньше
возмущает поле точечного заряда, чем
заземленная.
Действительно,
на
ней
происходит
только
перераспределение
зарядов.
Сила, действующая на заряд q ,
вычисляется как сумма сил, действующих со
стороны двух изображений
qq′
qq′′
q 2 R 3 (2l 2 − R 2 )
.
F=
+
=
−
⋅
4πε 0 (l − x) 2 4πl 2
4πε 0 l 3 (l 2 − R 2 ) 2
При l >> R сила взаимодействия
q 2 R3
F =−
⋅
,
2πε 0 l 5
убывает обратно пропорционально пятой степени расстояния, что также легко объяснимо:
величина индуцированного дипольного момента пропорциональна величине внешнего
поля (которое убывает обратно пропорционально квадрату расстояния), а величина поля
диполя убывает обратно пропорционально кубу расстояния.
Заметим, что в данном случае можно вычислить потенциал сферы, не рассчитывая распределения
зарядов на поверхности. По принципу суперпозиции, потенциал центра сферы равен сумме потенциалов
заряда q и индуцированных зарядов на поверхности сферы. Все индуцированные заряды находятся на
одном и том же расстоянии от центра и их сумма равна нулю, следовательно, равен нулю и потенциал,
создаваемый ими в центре сферы. Поэтому потенциал в центре сферы, следовательно, и в любой ее точке,
равен потенциалу поля точечного заряда
ϕ=
q
.
4πε 0 l
Суммарный заряд сферы остается равным нулю, но сфера приобретает
индуцированный дипольный момент, который равен дипольному моменту двух зарядовизображений
R3
p = q ′x = q 2 .
l
Перепишем эту формулу в виде
R3
q
p=q 2 =
ε 0 (4πR 3 ) = 3Vε 0 E 0 ,
l
4πε 0 l 2
4
q
- напряженность поля, создаваемого точечным
где V = πR 3 - объем сферы, E 0 =
3
4πε 0 l 2
зарядом в центре сферы. Таким образом, мы видим, что индуцированный дипольный
момент сферы пропорционален напряженности внешнего поля. В общем случае связь
между напряженностью внешнего поля и величиной индуцированного заряда записывают
виде
p = αε 0 E
где E - напряженность внешнего электрического поля, коэффициент пропорциональности
α имеет размерность объема и называется поляризуемостью тела. Мы показали, что для
проводящей сферы (аналогично шара), поляризуемость равна ее утроенному объему. В
170
общем случае поляризуемость зависит от формы тела и его электрических свойств, однако
по порядку величины она равна объему тела.
Достаточно интересно рассмотреть распределение потенциала в плоскости,
проходящей через точечный заряд и центр сферы. Эти потенциальные функции для
заземленной (а) и незаземленной (б) сфер изображены на рисунке 255. Функция,
описывающая потенциал поля, вне сферы совпадает с потенциалом поля точечных
зарядов (исходного и изображений), а внутри сферы равна нулю в случае (а) и постоянна в
случае (б) – круглые горизонтальные площадки совпадает с сечением сферы. Резкое
«возвышение» есть потенциал поля точечного заряда, который стремится к
бесконечности, здесь, как и на других рисунках, он «обрезан».
Проводящий шар в однородном поле.
Посмотрим, какие изменения внесет проводящий шар, помещенный в однородное
электрическое поле. Данная задача весьма популярна, известно несколько принципиально
различных методов ее решения. Мы же
воспользуемся уже полученными нами
результатами. Поместим шар посредине
между двумя одинаковыми по величине, но
противоположными по знаку точечными
зарядами + Q и − Q (рис. 256). Обозначим
расстояния от зарядов до центра шара l .
Построим изображения каждого заряда в шаре - два заряда, величины которых
R
R2
от центра шара. Теперь мысленно
равны q ′ = Q , и расположены на расстоянии x =
l
l
начнем уносить заряды Q на бесконечность l → ∞ . При этом заряды-изображения будут
приближаться к центру шара, образуя точечный диполь с дипольным моментом
QR 3
p = 2q ′x = 2 2 .
l
При увеличении расстояния между зарядами поле в области шара становится практически
однородным с напряженностью
Q
E=2
.
4πε 0 l 2
Выразим индуцированный дипольный момент шара через напряженность поля
p = 4πε 0 R 3 E ,
как видите, этот дипольный момент не зависит от «придуманных» зарядов Q и
расстояния l , поэтому и в однородном поле шар будет иметь такой же дипольный
171
момент. Обратите внимание, что и в данном случае поляризуемость шара равна его
утроенному объему.
Таким образом, поле индуцированных на поверхности шара зарядов эквивалентно
полю точечного диполя, находящегося в центре шара. Картину силовых линий такого
поля мы уже использовали ранее.
Неплохо также смотрится и
распределение потенциала (рис. 257).
Заметим,
что
потенциал
однородного
поля
изменяется
по
линейному
закону,
поэтому
распределение потенциала в таком поле
изображается наклонной плоскостью.
При помещении в это поле проводящего
шара на наклонной плоскости появляется
горизонтальная площадка, постоянного
потенциала на проводнике.
Задание для самостоятельной работы.
1. Найдите распределение поверхностной плотности индуцированных зарядов на
поверхности металлического шара, помещенного во внешнее электрическое поле.
172
10.5 Диэлектрики. Поляризация диэлектриков.
Вторая группа большая группа веществ, различаемых по их электрическим
свойствам – диэлектрики (изоляторы), вещества, не проводящие электрический ток. К
диэлектрикам относятся различные виды пластмасс, стекол, керамики, кристаллы солей,
сухая древесина, многие чистые жидкости (дистиллированная вода, масла, бензины), газы
при не очень сильных внешних полях. Все заряженные частицы, образующие данное
непроводящее вещество, связаны между собой и не способны передвигаться по объему
тела.
Заметим, что резкой границы между проводниками и изоляторами нет, так как все вещества в той
или иной степени способны проводить электрический ток, однако, во многих случаях слабой
проводимостью веществ можно пренебречь и считать их идеальными изоляторами. Возможность такого
приближения необходимо рассматривать в каждом конкретном случае отдельно. Заметим, что во многом
применимость модели идеального изолятора определяется временами протекания рассматриваемых
процессов, более подробно эта проблема будет рассмотрена позднее.
Так как все вещества состоят из электрически заряженных частиц, то все вещества
взаимодействуют с электрическим полем. В диэлектриках под действием электрического
поля заряды могут смещаться на незначительное расстояние, величина этого смещения
меньше размеров атомов и молекул. Тем не менее, эти смещения могут приводить к
весьма заметным последствиям, таки как появление индуцированных зарядов. В отличие
от проводников, в диэлектриках индуцированные заряды могут возникать как на их
поверхности, так и внутри их объема. Явление возникновения зарядов под действием
внешнего поля называется поляризацией диэлектрика, а сами возникающие заряды
называются поляризационными.
Существуют несколько механизмов поляризации диэлектрика, соответственно с
которыми различают несколько типов диэлектриков, некоторые из них мы сейчас кратко
рассмотрим.
Неполярные диэлектрики. К этому классу диэлектриков относятся вещества, состоящие
из атомов и молекул, не обладающих собственными дипольными моментами в отсутствии
поля. Типичными примерами таких веществ являются одноатомные благородные газы;
газы, состоящие из симметричных двухатомных молекул – кислород, водород, азот;
различные органические жидкости масла, бензины; из
твердых тел – пластмассы.
В молекулах этих веществ центры положительных
зарядов ядер и отрицательных зарядов электронных
облаков совпадают (рис. 258). Под действием внешнего
электрического
поля
происходит
незначительное
смещение центров этих зарядов, благодаря чему каждый
атом приобретает индуцированный дипольный момент,
направление которого совпадает с направлением внешнего
приложенного электрического поля. Величина этого дипольного момента сложным
образом зависит от напряженности внешнего поля. Однако в полях слабых по сравнению
с внутриатомными полями величина индуцированного дипольного момента оказывается
пропорциональной напряженности внешнего поля
r
r
p = αε 0 E ,
где коэффициент пропорциональности α называется поляризуемостью молекулы.
Справедливость такой записи обосновывается малостью смещения центров положительных и
отрицательных зарядов, а на малых изменениях любая функция может быть приближенно заменена на
линейную.
Задание для самостоятельной работы.
1. Оцените напряженность электрического поля внутри атома водорода.
173
Так как каждая молекула приобретает дипольный момент то и весь диэлектрик в
целом приобретает дипольный момент. Величина этого дипольного момента может
служить характеристикой степени поляризации диэлектрика. Однако более удобно ввести
«точечную» характеристику воздействия электрического поля на диэлектрик. Для этого
внутри диэлектрика небольшой объем ∆V , индуцированный дипольный момент этого
объема равен сумме дипольных моментов отдельных молекул, находящихся внутри
r
рассматриваемого объема
pi , отношение этого дипольного момента к объему
∑
i
называется поляризацией1 (вектором поляризации) диэлектрика
r
pi
r
P= i
.
(1)
∆V
Как обычно, данная характеристика становится «точечной», при объеме выделенной
части, стремящейся к нулю ( ∆V → 0 ).
Если индуцированный дипольный момент каждой молекулы пропорционален
напряженности внешнего поля, то и дипольный момент каждой части диэлектрика также
пропорционален напряженности внешнего поля. Поэтому связь между вектором
поляризации и напряженностью внешнего поля принято записывать в виде
r
r
P = χε 0 E ,
(2)
где χ (греческая буква «хи») – называется поляризуемостью вещества. Поляризуемость
вещества в отличии от поляризуемости тела и молекулы является безразмерной
величиной, характеризующей данное вещество. В отличие от проводников, где
воздействие поля характеризуется величиной индуцированных зарядов, для диэлектриков
такой характеристикой является дипольный момент единицы объема, то есть вектор
поляризации.
Рассмотренный механизм поляризации неполярных диэлектриков называется
индукционным.
∑
Формально из сравнения формул (1) и (2) следует, что поляризуемость вещества связана с
поляризуемостью отдельной молекулы соотношением χ = αn , (где n - число молекул в единице объема,
то есть концентрация). Однако такое простое соотношение справедливо только для разреженных газов, где
можно пренебречь взаимодействием молекул. В жидких и твердых телах каждая молекула находится в поле,
которое создается не только внешними источниками, но дипольными моментами других молекул. Иными
словами – та же «заклиненная» задача, только еще в более сложной постановке.
Задание для самостоятельной работы.
1. Считая, что поляризуемость молекулы равна ее объему оцените поляризуемость
молекул газов. Оцените также поляризуемость воздуха при нормальных условиях. Для
проведения оценок примите, что диаметр молекулы примерно равен 1 ангстрему.
Полярные диэлектрики. Некоторые молекулы
обладают
собственным дипольным моментом даже в отсутствии внешнего
электрического поля. Такие молекулы называются полярными,
а диэлектрики, образованные такими молекулами –
полярными. Полярные молекулы несимметричны, электронные
плотности в них смещены к одному из атомов.
Типичным примером такой молекулы служит молекула воды H 2 O , в которой
электронные облака смещены к атому кислорода, вследствие чего центры положительных
1
Обращайте внимание на терминологию: поляризация диэлектрика – явление, поляризация или вектор
поляризации – характеристика воздействия поля на вещество. Еще сложнее с поляризуемостью –
поляризуемость тела, поляризуемость молекулы, далее появится поляризация вещества.
174
и отрицательных зарядов смещены друг относительно друга, поэтому молекула обладает
собственным дипольным моментом (рис. 259).
Механизм поляризации полярных диэлектриков иной, чем неполярных. В
отсутствие внешнего поля дипольные моменты молекул ориентированы хаотически,
поэтому в любом объеме диэлектрика, содержащем достаточно много молекул,
суммарный дипольный момент равен нулю. Во внешнем электрическом поле на молекулы
действует вращающий момент, поэтому молекулы начинают ориентироваться, так, что
вектор дипольного момента выстраивается вдоль вектора напряженности внешнего поля
(рис. 260). Тем самым диэлектрик и каждая его часть приобретает индуцированный
дипольный момент. Такой механизм поляризации называется ориентационным. Полной
ориентации всех молекул препятствует хаотическое тепловое движение, поэтому
молекулы диэлектрика лишь частично ориентируются по внешнему полю.
Понятно, что в очень сильных полях подавляющая часть молекул выстроится вдоль
вектора напряженности внешнего поля. Однако при комнатных температурах степень
ориентации молекул является незначительной, поэтому и в случае полярных диэлектриков
можно приближенно считать, что вектор поляризации диэлектрика пропорционален
напряженности электрического поля
r
r
P = χε 0 E .
Отметим, что поляризуемость полярных диэлектриков на несколько порядков превышает
поляризуемость неполярных.
Заметим, что индукционный механизм поляризации присутствует и в полярных
диэлектриках. То есть под действием электрического поля происходит смещение зарядов
в молекулах, однако эффект ориентации на несколько порядков превосходит
индукционный эффект, поэтому последним часто пренебрегают.
Задание для самостоятельной работы.
1. Объясните, почему поляризуемость полярных диэлектриков зависит от температуры,
а неполярных практически нет. Как ведет себя поляризуемость полярных диэлектриков с
ростом температуры?
Электреты. Интересный класс веществ образуют диэлектрики, способные длительное
время сохранять наэлектризованное состояние и создающие собственное электрическое
поле в окружающем пространстве. Такие вещества называются электретами, они
аналогичны постоянным магнитам, сохраняющим состояние намагниченности.
Стабильные электреты можно получить, нагревая диэлектрик до температуры плавления,
а затем охлаждая их в сильном электрическом поле. В жидком состоянии полярные
175
молекул, находящиеся в электрическом поле, ориентируются, при отвердевании
подвижность молекул исчезает, поэтому ориентированное состояние молекул может
сохраняться длительное время. Изготавливают электреты из органических (воск, парафин,
нафталин, эбонит) и неорганических (сера, некоторые виды стекол) полярных
диэлектриков. Первые электреты были изготовлены в начале XIX века итальянским
физиком А. Вольта.
10.6 Описание электрического поля в диэлектриках.
Описание электрического поля в диэлектриках, помимо проблем, рассмотренных
при расчете полей в присутствии проводников, усложняется тем, что внутри диэлектриков
могут возникать объемные поляризационные заряды. Поэтому мы в состоянии
рассмотреть только простейшие задачи, связанные с описанием полей в присутствии
диэлектриков.
Прежде всего, мы ограничим рассмотрение однородными и изотропными
диэлектриками, то есть веществами, у которых поляризуемость одинакова во всех точках
и не зависит от направления поля. Кроме того, будем рассматривать электрические поля
только простейшей конфигурации.
Заметим, что среди диэлектриков существуют такие кристаллические диэлектрики, в которых
поляризуемость зависит от направления поля (анизотропия). Качественно понять такую зависимость можно
– смещение зарядов различно в различных направлениях. В таких диэлектриках направление вектора
поляризации может не совпадать с направлением вектора напряженности электрического поля.
Пусть во внешнее однородное электрическое поле помещена плоскопараллельная
пластина толщиной h , изготовленная из однородного диэлектрика, причем силовые
линии электрического поля перпендикулярны граням пластины.
Под действием электрического поля диэлектрик поляризуется, то есть происходит
смещение положительных и отрицательных зарядов. Схематически картину поляризации
можно представить следующим образом. Мысленно разделим
пластину на две – однородно заряженные (положительно и
отрицательно) вложенные друг в друга (рис.261). Объемные плотности
зарядов этих воображаемых пластин равны по модулю. Поэтому когда
платины полностью вложены одна в другую, то суммарная объемная
плотность заряда равна нулю. При наложении внешнего однородного
поля происходит малое смещение этих пластин друг относительно
друга. В области их перекрытия объемный заряд по-прежнему
отсутствует,
а
там
где
они
расходятся,
появляются
нескомпенсированные заряды. Так как смещения зарядов крайне малы, то можно считать,
что на поверхностях появляются поверхностные заряды, поверхностную плотность
которого обозначим σ . Заметим, что в данном случае поляризационные заряды не
создают электрического поля вне пластины, поэтому здесь поле остается неизменным.
Свяжем поверхностную плотность индуцированных поляризационных зарядов с
величиной вектора поляризации диэлектрика. Для этого выделим в пластине цилиндр,
основания которого (площадью ∆S ) расположены на гранях пластины. С одной стороны,
по определению вектора поляризации P , дипольный момент выделенного цилиндра равен
произведению модуля вектора поляризации на объем цилиндра ∆V = h∆S
p = P∆V = Ph∆S ,
а с другой, по определению дипольного момента, эта же величина равна произведению
заряда основания q = σ∆S , на расстояние между зарядами h
p = qh = σ∆Sh .
Из сравнения этих выражений следует замечательный результат: поверхностная
плотность поляризационных зарядов равна модулю вектора поляризации
диэлектрика:
σ = P.
(1)
176
В общем случае вектор поляризации диэлектрика может быть направлен под некоторым углом α к
поверхности. Также выделим внутри пластины наклонный цилиндр, основания которого находятся на
r
гранях пластины, а образующие параллельны вектору поляризации P . В этом
случае запишем нормальную к поверхности составляющую дипольного момента
выделенного цилиндра в двух формах:
-по определению вектора поляризации
pn = Pn ∆V = P cos α ⋅ h∆S ;
- по определению дипольного момента
p n = qh = σ∆Sh .
Из сравнения этих выражений следует, что поверхностная плотность
поляризационных зарядов равна нормальной составляющей вектора
поляризации диэлектрика:
σ = Pn .
(2)
Вернемся к расчету поля внутри диэлектрической пластины. Напряженность
электрического поля внутри пластины равно сумме
r
напряженностей внешнего поля E0 и поля, создаваемого
r
поляризационными зарядами E ′ (рис. 263)
r r
r
E = E0 + E ′ .
(3)
Напряженность поля поляризационных зарядов выражается
через поверхностную плотность зарядов σ
E′ =
σ
,
ε0
которая в свою очередь равна модулю вектора поляризации σ = P . Поляризация среды
определяется полем внутри нее, то есть величиной суммарной напряженности P = χε 0 E .
Подставляя значение напряженности E ′ в выражение (3), записанное в проекции на
направление внешнего поля получим
χε E
σ
P
(4)
E = E0 − E ′ = E0 −
= E0 −
= E0 − 0 .
ε0
ε0
ε0
Обратите внимание, искомая величина напряженности поля внутри диэлектрика
входит в обе части уравнения (4). Яркая иллюстрация «зацикленности» - поле внутри
зависит от индуцированных зарядов, индуцированные заряды зависят от поля внутри.
Однако в данном простейшем случае задача определения поля оказалась разрешимой.
Из уравнения (4) получаем
E
E
E= 0 = 0
(5)
1+ χ
ε
Из записанных соотношений также можно выразить поверхностную плотность
поляризационных зарядов
ε −1
(6)
σ = P = χε 0 E =
ε 0 E0 .
ε
В этих соотношениях обозначено ε = 1 + χ . Таким образом, поляризационные
заряды уменьшают поле внутри диэлектрика в (1 + χ ) раз по сравнению с внешним полем.
Величина ε = 1 + χ называется диэлектрической проницаемостью вещества. Именно
эта величина выступает в качестве основной характеристики электрических свойств
веществ и чаще всего приводится в справочниках физических величин.
Диэлектрическая проницаемость веществ может изменяться в широких пределах –
так для газов она отличается от единицы на величину порядка 10 −4 − 10 −6 (поэтому часто
диэлектрическими свойствами газов пренебрегают);
- для жидких и твердых неполярных диэлектриков она составляет несколько единиц
(например, для керосина ε = 2 );
177
- для полярных диэлектриков несколько десятков единиц (например, для воды ε = 81 );
- есть вещества, для которых диэлектрическая проницаемость составляет величины
порядка десятков и сотен тысяч (эти вещества называются сегнетоэлектриками, с ними мы
в следующем учебном году).
Диэлектрическая проницаемость вещества показывает, во сколько раз это вещество
уменьшает напряженность электрического поле, при условии, что силовые линии поля
перпендикулярны поверхности диэлектрика. Конечно, это уменьшение связано с тем, что
на поверхности диэлектрика возникают поляризационные заряды, поле которого
направлено противоположно внешнему полю, породившему эти заряды.
Особо подчеркнем, что поле внутри диэлектрического тела зависит от:
r
- внешнего поля E 0 ;
- диэлектрической проницаемости вещества;
- формы тела.
Утверждение о том, что диэлектрик всегда уменьшает поле в ε раз, мягко говоря, не всегда
справедливо, оно верно тогда когда силовые линии перпендикулярны границам тела, или если эти границы
находятся так далеко, что полем поляризационных зарядов можно пренебречь.
r
Пусть теперь внешнее однородное поле E 0
направлено под некоторым углом α к нормали
поверхности пластины (рис. 264). Напряженность
поля внутри пластины и в этом случае сумме
r
напряженностей внешнего поля E0 и поля,
r
создаваемого поляризационными зарядами E ′
r r
r
E = E0 + E ′ .
Напряженность
поля
создаваемого
r
E′
направлено
поляризационными зарядами
r
перпендикулярно поверхности пластин (не совпадает с направлением внешнего поля E0 ),
поэтому вектор напряженности электрического поля внутри пластины направлен под
другим углом к поверхности пластины.
Для определения поля разложим векторы
напряженности полей вне и внутри пластины на
r
r
нормальные (перпендикулярные к поверхности) E 0 n , E n
r
r
и тангенциальные (параллельные поверхности) E 0τ , Eτ
составляющие
(рис.
265).
Согласно
принципу
суперпозиции
эти
компоненты
поля
можно
рассматривать независимо.
Случай нормальных составляющих мы уже рассмотрели
и показали, что для напряженностей полей выполняется
E
соотношение E n = 0 n , которое можно переписать в
ε
виде
E 0 n = εE n .
(7)
Так как поляризационные заряды создают поле, вектор напряженности которого
направлен перпендикулярно поверхности, то тангенциальные составляющие полей вне и
внутри пластины будут равны
E 0τ = Eτ .
(8)
Соотношения (7) и (8) определяют законы изменения векторов напряженностей
полей на границе диэлектрика (задают граничные условия). Они играют важную роль
при расчетах полей в присутствии диэлектриков.
Выразим модуль вектора напряженности поля внутри диэлектрика
178
2
E
⎛ E cos α ⎞
2
E= E +E = ⎜ 0
⎟ + (E 0 sin α ) = 0 cos 2 α + ε 2 sin 2 α .
ε
ε
⎝
⎠
Как видите, вектор напряженности поля внутри диэлектрика не только не
совпадает по направлению с напряженностью внешнего поля, но и его модуль зависит от
угла, между напряженностью внешнего поля и вектором нормали к поверхности
диэлектрика.
2
n
2
n
Задания для самостоятельной работы.
1. Покажите, что на плоской границе двух диэлектриков с
диэлектрическим проницаемостями ε 1 и ε 2
для нормальных
составляющих векторов напряженностей полей выполняется граничное
условие ε 1 E1n = ε 2 E 2 n (рис. 266).
2. Найдите соотношение между углами, которые образуют векторы
напряженностей полей с нормалью к границе раздела двух диэлектриков.
Если проводящее тело находится внутри диэлектрика, то на границе проводника и
диэлектрика возникают поляризационные заряды, которые уменьшают поле внутри
диэлектрика. Найдем поверхностную плотность этих зарядов. Пусть в некоторой точке
поверхности проводника поверхностная плотность заряда равна σ 0 , тогда напряженность
поля, создаваемого зарядами на проводнике определяется выражением E 0 =
σ0
. Это поля
ε0
выступает в качестве внешнего по отношению к диэлектрику и направлено
перпендикулярно границе диэлектрика. Поэтому согласно формуле (6) поверхностная
плотность поляризационных зарядов на диэлектрике равна
ε −1
ε −1
σ′=
ε 0 E0 =
σ0.
ε
ε
Понятно, что эти заряды противоположны по знаку зарядам на проводнике,
поэтому суммарная поверхностная плотность заряда в данной точке границы равна
σ 0 −σ ′ =
σ0
.
ε
Вот еще одно явное объяснение уменьшения поля в диэлектрике – на границе проводника
и диэлектрика возникают поляризационные заряды противоположного знака, при этом
суммарный поверхностный заряд уменьшается в ε раз, соответственно во всех точках
внутри диэлектрика поле также уменьшается во столько же раз (конечно, если пренебречь
полем зарядов, возникающих на других границах диэлектрика).
Если два небольших заряженных тела (которые можно считать точечными
зарядами) находятся внутри бесконечного диэлектрика, то сила взаимодействия между
ними уменьшается, по сравнению с силой взаимодействия в вакууме. На границе раздела
заряженных тел и диэлектрика возникают поляризационные заряды, которые частично
экранируют поля, создаваемые точечными зарядами. Как мы показали, напряженность
поля, создаваемого одним из зарядов, уменьшается в ε раз, по сравнением с полем в
вакууме. Поэтому сила, действующая на второе тело, также уменьшается в ε раз.
Заметьте, что речь идет о силе, действующей на само заряженное тело, без учета сил,
действующих на поляризационные заряды, возникшие вблизи этого тела. Ведь эти
поляризационные заряды «привязаны» к диэлектрику, а не к рассматриваемому телу.
Поэтому сила взаимодействия двух точечных зарядов, находящихся в однородном
бесконечном диэлектрике рассчитывается по формуле
q1 q 2
F=
.
4πε 0 εr 2
179
В некоторых учебных и справочных пособиях по физике именно эту формулу приводят в качестве
формулировки закона Кулона. Однако, такое расширение закона Кулона нельзя признать
удовлетворительным. Во-первых, эта формула получена как следствие применения законов электрического
поля и свойств веществ, во-вторых, ее применение требует значительных оговорок – диэлектрик должен
быть бесконечным, однородным, для него должна выполняться линейная связь между напряженностью поля
и поляризацией диэлектрика. Далее, диэлектрическая проницаемость является усредненной
характеристикой вещества, она никоим образом не учитывает атомную структуру строения материи – очень
интересный вопрос: «чему равна сила взаимодействия между двумя электронами, находящимися в воде?»,
ведь размеры электрона намного меньше размеров молекулы воды. Поэтому разумно формулировать, как
постулат (подтверждаемый экспериментально) закон Кулона, как закон взаимодействия точечных зарядов в
вакууме, а влияние среды на взаимодействие заряженных тел рассматривать отдельно, и полученные
результаты рассматривать как следствие из закона Кулона и электрических свойств среды.
10.7 Метод изображений для диэлектриков.
Идеи метода изображений, развитые для описания поля в присутствии
проводников, могут быть распространены и для описания поля в присутствии
диэлектриков. Существенным отличием этих методов в случае диэлектриков является
изменение (существенное усложнение) граничных условий. Если поверхность металла
является эквипотенциальной, то на поверхности диэлектрика должны выполняться
составляющих векторов
граничные условия для нормальных и тангенциальных
напряженности полей (7)-(8). Поэтому чаще всего приходится «угадывать» вид
распределения поверхностной плотности поляризационных зарядов, что удается сделать
только в редких случаях.
Рассмотрим для примера электрическое поле создаваемое точечным зарядом q ,
который находится на расстоянии h от бесконечной плоской границы с бесконечным
диэлектриком с проницаемостью ε .
Предположим, что на плоской границе диэлектрика, взаимодействующего с
точечным зарядом q , возникают поляризационные заряды, распределение σ ′ которых
совпадает с распределением зарядов на поверхности проводника, находящегося в
аналогичных условиях. Такое распределение
поверхностных
зарядов,
создает
в
полупространстве поле, эквивалентное полю
точечного заряда. Таким образом, будем
рассматривать
поле
в
верхнем
полупространстве над диэлектриком как
суперпозицию зарядов q и q′ , расположенных
симметрично по разные стороны от границы, а
поле внутри диэлектрика как поле двух
точечных зарядов q и q′ , расположенных в
одной точке (рис. 267).
Для того, чтобы доказать справедливость нашего предположения необходимо
добиться выполнения граничных условий
E 0 n = εE n ;
E 0τ = Eτ .
Легко видеть, что условие постоянства тангенциальной составляющей
выполняется при любом значении заряда-изображения q′ . Попытаемся подобрать такую
величину этого заряда, что бы выполнялось граничное условие и для нормальных
составляющих поля. Согласно нашему предположению, в пространстве над диэлектриком
возле границы нормальная составляющая поля определяется формулой
q − q′
cosθ ,
E0n =
4πε 0 R 2
а внутри диэлектрика, непосредственно у границы
180
q + q′
cos θ .
4πε 0 R 2
Граничное условие для нормальных составляющих поля E 0 n = εE n будет выполняться в
любой точке границы, если положить q − q′ = ε (q + q′) , или
ε −1
.
(1)
q′ = −q
ε +1
Итак, мы показали, что предположение о характере распределения поляризационных
зарядов на границе диэлектрика справедливо, так как выполняются оба граничные
условия.
Таким образом, для расчета полей приходится строить заряд-изображение,
расположенный внутри диэлектрика , если рассчитывается поле вне его; и наоборот
снаружи от диэлектрика, если рассматривается поле внутри его.
Отметим, что поле внутри диэлектрика в данном случае совпадает с полем
2
точечного заряда, величина которого равна q + q′ =
, соответственно, напряженность
ε +1
r r
r
2 r
поля внутри диэлектрика равна E = E 0 + E ′ =
E 0 . То есть диэлектрик уменьшает
ε +1
поле, но не в ε раз, как это бывает в случае бесконечного диэлектрика, или когда силовые
линия поля перпендикулярны границе. Поле вне диэлектрика отличается от поля
точечного заряда.
Аналогично может быть решена задача о расчете поля, создаваемого
диэлектрическим шаром, помещенным во внешнее однородное электрическое поле.
Оказывается, что и в этом случае вид распределения поляризационных зарядов на
поверхности шара совпадает с видом распределения индуцированных зарядов на
поверхности проводящего шара. Использование этого обстоятельства позволяет найти
напряженности полей как внутри шара, так и вне его. Суммарное поле внутри шарика
будет оставаться однородным и направленным так же, как и внешнее поле, однако его
величина будет меньше
r r
r
3 r
E = E0 + E ′ =
E0 .
(2)
ε +2
Поле вне шара перестанет быть однородным.
Обратите внимание, что множитель, показывающий во сколько раз изменилась
напряженность поля, отличается от аналогичного множителя для случая плоской границы
- форма границы оказывает существенное влияния на поле внутри и снаружи от
диэлектрика.
En =
Заметим, что переход от диэлектрика к проводнику в задачах электростатики может быть
осуществлен, полагая ε → ∞ , действительно, в этом пределе формулы определяющие заряды-изображения
и напряженности полей в диэлектрике, переходят в соответствующие формулы, полученные ранее для
проводника2.
Если же положить ε = 1 , то все индуцированные заряды исчезают, как и должно быть в отсутствие
диэлектрика.
Задание для самостоятельной работы.
1. Докажите формулу (2),
2
Обратный переход от проводника к диэлектрику невозможен. Иными словами, «уйти на бесконечность
легко, вернуться трудно!»
181
§ 11 Постоянный электрический ток.
Мы подробно рассмотрели свойства электростатического поля, порождаемого
неподвижными электрическими зарядами. При движении электрических зарядов
возникает целый ряд новых физических явлений, к изучению которых мы приступаем.
В настоящее время широко известно, что электрические заряды имеют дискретную
структуру, то есть носителями зарядов являются элементарные частицы – электроны,
протоны и т.д. Однако в большинстве практически значимых случаев эта дискретность
зарядов не проявляется, поэтому модель сплошной электрически заряженной среды
хорошо описывает явления, связанные с движением заряженных частиц, то есть с
электрическим током.
Электрическим током называется направленное движение заряженных
частиц.
С использованием электрического тока вы хорошо знакомы, так как электрический
ток чрезвычайно широко используется в нашей жизни. Не секрет, что наша нынешняя
цивилизация в основном базируется на производстве и использовании электрической
энергии. Электрическую энергию достаточно просто производить, предавать на большие
расстояния, преобразовывать в другие требуемые формы.
Кратко остановимся на возможных проявлениях действия электрического тока.
Тепловое действие электрического тока проявляется практически во всех
случаях протекания тока. Благодаря наличию электрического сопротивления при
протекании тока выделяется теплота, количество которой определяется законом ДжоуляЛенца, с которым вы должны быть знакомы. В некоторых случаях выделяемая теплота
полезна (в разнообразных электронагревательных приборах), часто выделение теплоты
приводит к бесполезным потерям энергии при передаче электроэнергии.
Магнитное действие тока проявляется в создании магнитного поля, приводящего
к появлению взаимодействия между электрическими токами и движущимися
заряженными частицами.
Механическое действие тока используется в разнообразных электродвигателях,
преобразующих энергию электрического тока в механическую энергию.
Химическое действия проявляется в том, что протекающий электрический ток,
может инициировать различные химические реакции. Так, например, процесс
производства алюминия и ряда других металлов основан на явлении электролиза –
реакции разложения расплавов оксидов металлов под действием электрического тока.
Световое действие электрического тока проявляется в появлении светового
излучения при прохождении электрического тока. В некоторых случаях свечение является
следствие теплового разогрева (например, в лампочках накаливания), в других
движущиеся заряженные частицы непосредственно вызывают появление светового
излучения.
В самом названии явления (электрический ток) слышны отголоски старых физических воззрений,
когда все электрические свойства приписывались гипотетическое электрической жидкости, заполняющей
все тела. Поэтому при описании движения заряженных частиц используется терминология аналогичная
используемой при описании движения обычных жидкостей. Указанная аналогия простирается дальше
простого совпадения терминов, многие законы движения «электрической жидкости аналогичны законам
движения обычных жидкостей, а частично знакомые вам законы постоянного электрического тока по
проводам аналогичны законам движения жидкости по трубам. Поэтому настоятельно рекомендуем вам
повторить раздел, в котором описаны эти явления – гидродинамику.
11.1 Характеристики электрического тока.
Все заряженные тела взаимодействуют друг с другом посредством электрических
сил, которые для неподвижных частиц описываются законом Кулона. При относительном
движении заряженных частиц сила взаимодействия изменяется. Следовательно,
движущиеся частицы создают поле, отличное от электростатического, такое поле
называется магнитным. Если заряженные частицы движутся хаотически, то суммарное
магнитное поле оказывается равным нулю. Поэтому при описании движении заряженных
182
частиц наибольший интерес представляет усредненное направленное движение,
приводящее к переносу электрического заряда.
В настоящее время широко известно, что электрические заряды имеют
дискретную структуру, то есть носителями зарядов являются элементарные частицы –
электроны, протоны и т.д. Однако в большинстве практически значимых случаев эта
дискретность зарядов не проявляется, поэтому модель сплошной электрически
заряженной среды хорошо описывает явления, связанные с движением заряженных
частиц, то есть с электрическим током.
В электростатике мы ввели понятие объемной плотности
электрического заряда ρ , как усредненной характеристики
распределения дискретных точечных зарядов. В рамках этой же
модели можно говорить о движении зарядов как о движении
некоторой сплошной среды и использовать математический
аппарат, рассмотренный нами при описании движения жидкости,
то есть ввести понятия скорости движения «электрической
жидкости в данной точке», векторного поля скоростей, линиях
тока и т.д. Однако нас интересует не столько движение самой
«электрической жидкости», сколько электрический заряд переносимый ею.
Рассмотрим некоторую пространственную область, в которой движутся
электрические заряды («электрическая жидкость»), на рисунке изображены линии тока
этого движения. Выделим в этой области малую площадку площадью ∆S
перпендикулярную линиям тока (рис. 268). Пусть скорость
r
движения заряда в пределах площадки равна v . За промежуток
времени ∆t через площадку пройдет заряд, заключенный в
объеме параллелепипеда длиной v∆t , опирающийся на
выбранную площадку (рис. 269). Величина этого заряда равна
∆q = ρv∆t∆S . Чтобы определить «точечную» характеристику
переноса заряда разделим величину заряда, прошедшего через
площадку, на площадь площадки и рассматриваемый промежуток
времени. Полученная таким образом характеристика называется плотностью
электрического тока
∆q
(1)
j=
= ρv .
∆t∆S
Имеет смысл считать данную характеристику векторной, направление которой совпадает
с направлением скорости движения зарядов
r
r
j = ρv .
(2)
Таким образом, плотностью электрического тока называется векторная
физическая величина, модуль которой равен количеству электрического заряда,
протекающего в единицу времени через площадку единичной площади,
расположенную перпендикулярно направлению движения заряда, а направление
совпадает с направлением переноса электрического заряда.
Для того чтобы плотность тока была определена «в каждой
точке», рассмотренную площадку следует сделать бесконечно
малой.
Рассмотрим определение плотности электрического тока с
точки зрения дискретного описания. Выделим
в объеме
движения дискретных зарядов небольшую часть объемом ∆V ,
содержащую достаточно много заряженных частиц (рис. 270).
Пронумеруем все заряженные частицы, находящиеся в этом
объеме; обозначим величины зарядов этих частиц q k , а их
183
r
r
скорости v k ( k = 1,2,3...N ). Построим векторную сумму J =
∑
r
q k v k . Если движение
k
заряженных частиц является хаотическим, то есть скорости частиц равновероятно
направлены во все стороны, то данная сумма будет приблизительно равна нулю, если же в
движении заряженных частиц присутствует преимущественное направление, то
построенная величина будет указывать направление переноса заряда и характеризовать
количество этого заряда. Чтобы построенная таким образом характеристика была
точечной, необходимо разделить ее на величину выделенного объема и устремить
последний к нулю
∑
r
j =
r
qkvk
k
.
∆V
(3)
Покажем теперь, что построенная таким образом величина совпадает с определенной
нами выше плотностью тока. Для простоты будем считать, что все заряженные частицы
Определим среднюю
одинаковы q k = q (например, электроны в металле).
r
vk
r
арифметическую скорость движения частиц
, из которого следует, что
v = k
N
r
r
v k = N v . С учетом этого выражения, формула преобразуется к виду
∑
∑
k
r
j=
∑q v
k
k
∆V
r
q
k
=
∑v
r
k
∆V
k
=
r
qN v
∆V
r
= qn v ,
(4)
N
- число заряженных частиц в единице объема, то есть их
∆V
концентрация. Произведение же концентрации частиц на их электрический заряд равно
электрическому заряду, заключенному в единице объема, то есть объемной плотности
заряда qn = ρ . Таким образом, формула (4) совпадает с формулой (2), если скорость
движения «электрической жидкости» отождествить со средней скоростью движения
заряженных частиц.
где обозначено n =
В качестве наглядной модели движения заряженных частиц можно представить движения облака
комаров, каждый из которых движется хаотически в пределах облака, а под действием ветерка это облако
целиком смещается в некотором направлении.
Если в переносе заряда участвует несколько типов заряженных частиц, то можно
определить плотность тока каждого типа части, а суммарную плотность тока, как сумму
плотностей токов всех типов частиц. Так в растворе поваренной соли могут двигаться
положительно заряженные ионы натрия Na + и отрицательно заряженные ионы хлора
Cl − . В этом случае вектор плотности тока выражается суммой
r r+ r−
r
r
j = j + j = q+n+ v + + q−n− v − ,
(5)
r+ r−
r
r
где j , j - плотности токов, q + , q − - заряды, n + , n − - концентрации, v + , v − - средние
скорости ионов натрия и хлора, соответственно.
Заметим, что согласно данному определению вектор плотности тока совпадает со
скоростью движения положительных зарядов, при движении отрицательных зарядов
вектор плотности тока противоположен вектору их скорости. Иными словами за
положительное направление движения электрического тока принимается направление
движения положительных зарядов.
В большинстве применений электрический ток проходит по металлам, в которых носителями тока
являются отрицательно заряженные электроны, поэтому, как ни странно, чаще всего направление тока
противоположно направлению движения реальных частиц электронов. Такая несуразность также является
184
следствием исторической традиции – направление электрического тока было определено еще в начале XIX
века, когда о природе носителей тока не имели ни малейшего представления.
Таким образом, мы определили векторную характеристику переноса заряда –
плотность тока. Этот вектор определен в каждой точке пространства,
поэтому с
r
математически движение зарядов описывается векторным полем j ( x, y, z ) .
Рассмотрим физический смысл потока1 данного
векторного поля. Для этого мысленно выделим малую
площадку площадью ∆S , в пределах которой вектор плотности
r
тока j можно считать постоянным и направленным под углом
r
α к вектору нормали площадки n (рис. 271). Если скорость
направленного движения заряда равна v , то за время ∆t через
площадку пройдет заряд, содержащийся в наклонном
параллелепипеде, длина стороны которого равна v∆t . Величина
этого заряда равна произведению объемной плотности заряда на
объем параллелепипеда ∆q = ρ∆Sh = ρ∆Sv∆t cos α . Следовательно, в единицу времени
через площадку протекает электрический заряд равный
r r
∆q
I=
= ρ∆Sv cos α = j∆S cos α = j ⋅ n∆S = Φ j .
(6)
∆t
Как следует из полученного соотношения, rданная
величина равна потоку вектора плотности тока j через
площадку ∆S . Если требуется найти количество заряда
протекающего через некоторую поверхность (рис. 272), в
пределах которой вектор плотности тока изменяется, то
следует поступать традиционным образом: разбить
поверхность на малые площадки, найти по формуле (6)
поток
через
каждую
площадку,
после
чего
просуммировать эти потоки
r r
Φj =
∆Φ jk =
j k ⋅ n k ∆S k .
∑
k
∑
k
Поток вектора плотности тока играет важную роль в изучении электрического тока,
поэтому получил «персональное» наименование – сила электрического тока.
Силой электрического тока называется заряд, протекающий через площадку в
∆q
единицу времени: I =
.
∆t
По определению, сила тока является скалярной физической величиной,
описывающей движение электрических зарядов усреднено – являясь характеристикой,
описывающей свойства тока в пределах некоторой площадки целиком, без конкретизации
распределения в пределах рассматриваемой поверхности.
При течении электрического тока по проводам, распределения тока в поперечном
сечении провода мало интересно – вполне достаточно знать значение суммарного тока
через поперечное сечении провода, так эта физическая величина позволяет находить
интересующие характеристики – мощность, передаваемую энергию и так далее. Поэтому
часто именно силу электрического тока определяют как заряд, протекающий через
поперечное сечение проводника в единицу времени и считают основной
характеристикой электрического тока.
Как уже отмечалось ранее единица силы электрического тока Ампер (обозначается
А), является основной единицей международной системы единиц СИ. Строгое
определение этой единицы мы дадим позднее, на основании закона взаимодействия
электрических токов. Характерные значения сил токов, используемых в бытовых
1
Речь идет, конечно, о математическом понятии потока векторного поля.
185
приборах, составляют величины порядка одного ампера, так лампочка накаливания
мощностью 100 Вт потребляет электрический ток немного меньше, чем 0,5 А.
Оценим скорость направленного движения электронов в металлических проводниках.
Ранее мы оценили концентрацию свободных электронов в меди, получив значение
n ≈ 8 ⋅ 10 22 см −3 = 8 ⋅ 10 28 м −3 . Если электрический ток силой в I = 1A протекает по медному
проводнику с площадью поперечного сечения S ≈ 1 мм 2 , то для оценки средней скорости
движения электронов (заряд которых
e ≈ 1,6 ⋅ 10 −19 Кл )
можно воспользоваться
соотношением
I = jS = en v S , из которого следует
I
м
1А
=
≈ 8 ⋅ 10 −5 ,
−19
−3
−6
28
2
enS 1,6 ⋅ 10 Кл ⋅ 8 ⋅ 10 м ⋅ 1 ⋅ 10 м
с
то есть составляет очень малую величину порядка одной десятой доли миллиметра в
секунду. При силе тока в 10А скорость направленного движения электронов «достигает»
величины порядка миллиметра в секунду! И при таких мизерных скоростях эти
движущиеся электроны переносят значительную энергию.
v =
Во избежание возможных недоразумений, подчеркнем, что мы оценили скорость направленного
движения электронов, а не скорость распространения тока. При подключении сети к источнику тока
движение зарядов во всех проводниках начинается практически мгновенно – электрическое поле,
заставляющее двигаться электроны, распространяется по проводнику со скоростью света (триста тысяч
километров в секунду). Аналогично, при открывании водопроводного крана практически мгновенно вся
вода в трубе начинает двигаться - упругие силы, приводящие воду в движение, распространяются со
скоростью звука в воде (несколько тысяч километров в секунду), хотя вода может двигаться по трубе очень
медленно.
11.2 Закон Ома.
В данном разделе нам предстоит выяснить причины возникновения направленного
движения заряженных частиц, то есть электрического тока. Природа электрического тока
в различных проводящих средах (металлах, электролитах, газах и т.д.) различна –
носителями тока могут выступать разные заряженные частицы, силы, действующие на
них со стороны окружающей среды, так же различаются. Подробное изучение
электропроводящих свойств различных веществ мы проведем позднее. Сейчас наша
задача установить ряд общих закономерностей, присущих протеканию электрического
тока в различных средах. В качестве основного объекта нашего нынешнего рассмотрения
будет выступать электрический ток в металлах. Мы уже оговаривали в общих чертах
строение металлов. Все металлы в твердом состоянии имеют кристаллическую структуру,
образованную ионами - атомами, потерявшими один или два электрона. Эти электроны
(их также называют свободными) «обобществляются», то есть могут перемещаться,
«блуждать», по кристаллической решетке в пределах всего объема металлического тела
(рис.273).
При отсутствии внешнего воздействия свободные электроны хаотически движутся,
такое движение называется тепловым, скорость его возрастает с ростом температуры. Для
того чтобы заставить электроны двигаться направлено, к ним необходимо приложить
186
внешнюю силу. В качестве такой силы чаще всего выступает сила со стороны
электрического поля.
При изучении электростатики мы утверждали, что электрическое поле внутри проводника
отсутствует. Но не забывайте, электростатика рассматривает условия равновесия, когда индуцированные
внешним полем заряды создают собственное поле, которое полностью компенсирует внешнее поле. Можно
сказать, что сейчас мы рассматриваем процесс перехода к этому равновесному состоянию, и условия, при
которых процесс движения электрических зарядов может продолжаться сколь угодно долго.
r
Итак, если внутри проводника создано электрическое поле напряженности E , то
свободные электроны
начинают двигаться с ускорением, определяемым вторым законом
r
r eE
Ньютона2 a =
(где e - заряд электрона, m - его масса) и направленным по
m
направлению внешнего поля. При увеличении скорости электрона он чаще сталкивается с
ионами кристаллической решетки, отдавая ей часть своей кинетической энергии. Эта
энергия, передаваемая решетке, идет на увеличение энергии ее движения, то есть
увеличение тепловой, внутренней энергии метала, благодаря чему его температура
возрастает. Наличие неупругих столкновений свободных электронов с ионами решетки
приводит к тому, что средняя скорость направленного движения не растет неограниченно,
а стабилизируется.
Для упрощенного описания движения электронов примем, что в течение
некоторого промежутка времени τ электрон движется без столкновений, а затем в
результате неупругого столкновения полностью отдает свою кинетическую энергию иону
решетки. Введенное время τ имеет смысл среднего времени движения электрона между
столкновениями. В рамках такой модели
между столкновениями скорость электрона
r
r
r
eE
τ . Так как мы считаем движение электрона
возрастает от v = 0 до v max = aτ =
m
равноускоренным,
то средняя скорость направленного движения электрона равна
r
r
1r
eE
v = v max =
τ . Следовательно, плотность электрического тока описывается
2
2m
формулой
r
r
e 2 nτ r
j = en v =
E.
(1)
2m
Таким образом, мы приходим к выводу, что плотность электрического тока
оказывается пропорциональной напряженности электрического поля.
Этот же результат можно получить в рамках несколько иной модели. Будем считать, что при
движении заряженной частицы со стороны окружающей среды действует тормозящая сила,
пропорциональная
скорости
движения
частицы
r
r
Fсопр. = − βv . Под действием
электрического поля скорость электрона будет возрастать до тех пор, пока сила
сопротивления не уравновесит силу, со стороны электрического поля (рис. 274). Таким
образом, в установившемся равномерном движении выполняется соотношение
r
r
r r
r
Fсопр. + eE = − βv + eE = 0 ,
из которого также следует, что скорость установившегося движения (а, следовательно, и плотность тока)
пропорциональны напряженности действующего электрического поля
r
r e2n r
j = env =
E
β
(2)
Две рассмотренные модели не противоречат друг другу. Фактически, в рамках второй модели
рассматривается движение, усредненное по промежутку времени, превышающему среднее время между
2
Строго говоря, движение электронов внутри кристаллической решетки подчиняется законам квантовой
физики (физики микрочастиц). Однако, качественное описание и объяснение законов электрического тока
может быть дано в рамках классических моделей движения этих частиц.
187
столкновениями. Для полного согласования результатов необходимо принять, что коэффициент
пропорциональности между силой сопротивления среды и средней скоростью электрона равен
β=
2m
τ
.
Рассмотренные модели, как мы подчеркивали, носят качественный характер,
поэтому основной вывод о пропорциональности между плотностью тока требует
экспериментальной проверки. Более того, введенные параметры τ и β не могут быть
измерены экспериментально. Запишем полученные выражения в общепринятом виде
r 1 r
r
j = λE = E ,
(3)
ρ
где введенные коэффициенты характеризуют свойства проводящей среды и называются:
ρ - удельное электрическое сопротивление, λ - удельная проводимость среды.
Удельное электрическое сопротивление является макроскопическое характеристикой вещества,
описывающей его свойства усреднено, в рамках рассмотренных нами моделей оно может быть выражено
через микроскопические характеристики строения металла
2m
β
= 2 .
(4)
2
e nτ e n
Применим формулу (3) для расчета силы электрического тока по проводящей
проволоке. Выделим участок проволоки длиной l , площадь поперечного сечения
проволоки обозначим S . Если электрическое поле внутри проволоки является
r
однородным, то и плотность электрического тока j также будет постоянна во всех точках
проводника. В этом случае сила тока через поперечное сечения проволоки будет равна
произведению плотности тока на площадь поперечного сечения I = jS . Для плотности
тока используем выражение (3), тогда силу тока можно представить в виде
S
U
1
I = jS = ES =
El =
,
(5)
ρ
ρl
R
где обозначено U = El = ∆ϕ - разность потенциалов между концами рассматриваемого
участка, которая в данном случае также называется электрическим напряжением3;
l
R=ρ
(6)
S
1
электрическое сопротивление участка проводника. Обратная величина Λ =
называется
R
электрической проводимостью участка.
Формула (5) может быть легко проверена экспериментально, так как достаточно
давно разработаны простые и знакомые вам приборы для измерения силы тока
(амперметры) и электрического напряжения (вольтметры). Многократно проведенные
исследования (в том числе многочисленными учащимися средних школ) действительно
свидетельствуют, что для многих веществ, в том числе для металлов, это соотношение
выполняется с высокой степенью точности.
Впервые экспериментально эта зависимость была установлена в 1826 году
немецким физиком Георгом Симоном Омом, поэтому носит название закона Ома для
участка цепи. Связанное с ним соотношение между плотностью тока и напряженностью
поля (3) носит название закона Ома в дифференциальной форме.
Установленный закон Ома не носит универсального характера – имеется целый ряд
веществ (газы, полупроводники) и электронных устройств, для которых связь между
током и напряжение носит более сложный характер.
ρ=
Еще раз подчеркнем аналогию между законами электрического тока и законами движения
жидкости. Так закон Ома может быть сформулирован в виде аналогичном формуле Пуазейля для движения
вязкой жидкости по трубе:
3
Между разностью потенциалов и электрическим напряжением есть различие, о котором мы поговорим
немного позднее, но в данном случае они совпадают.
188
сила электрического тока, т.е. заряд, протекающий через поперечное сечение проводника (расход
жидкости, то есть объем жидкости, протекающей через поперечное сечение трубы) пропорционален
разности потенциалов, приложенной к концам проводника (разности давлений, приложенной к концам
трубы). Причина такой аналогии заключается в том, что и движению зарядов и движению жидкости
препятствуют силы сопротивления (вязкого трения), которые пропорциональны скорости движения.
11.3 Закон Джоуля-Ленца.
Рассмотренному закону Ома для участка цепи можно дать энергетическое
истолкование. Действительно, по определению, разность потенциалов (напряжение) равна
работе, которую совершает электрическое поле по перемещению единичного
положительного заряда. При движении заряженных частиц в среде необходимо
преодолевать силы сопротивления среды, поэтому для поддержания постоянного тока к
движущимся частицам постоянно необходимо прикладывать внешнюю силу. Очевидно,
что работа электрического поля по перемещению заряда по проводнику пропорциональна
силе сопротивления, которая в свою очередь пропорциональна скорости движения
заряженных частиц, или силе тока. Именно поэтому сила тока оказывается
пропорциональной приложенному напряжению. В таком установившемся режиме работа
электрических сил по перемещению заряженных частиц тратится на увеличение
внутренней
энергии среды. Заметим, что в некоторых случаях электрическое
сопротивление обусловлено не только неупругими столкновениями электронов с
кристаллической решеткой, но и иными причинами. Так при работе электрического
двигателя на движущиеся электроны действую тормозящие силы со стороны магнитного
поля, в этом случае работа электрического поля равна механической работе, совершаемой
двигателем.
Приведем еще одну простую механическую аналогию. Если тело движется только под действием
только одной постоянной силы, то его движение является равноускоренным и вся работа этой силы идет на
увеличение кинетической энергии тела. Если же тело движется в вязкой среде, то на него также действует
сила вязкого трения, пропорциональная скорости. Поэтому по прошествии некоторого промежутка времени
после начала движения, скорость тела становится постоянной. Так, например, при движении лодки в воде ее
скорость пропорциональна мощности двигателя (то есть работе, совершаемой двигателем). В
установившемся режиме кинетическая энергия тела также как и скорость остается постоянной, а работа
внешней силы расходуется на увеличение внутренней энергии среды.
Если среда не обладает электрическим сопротивлением, то для создания
постоянного тока постоянное электрическое поле не требуется – достаточно заряженным
частицам сообщить некоторую скорость, а дальше они будут двигаться по инерции. Таким
образом, в установившемся режиме работа электрического поля по поддержанию
постоянного тока равна увеличению энергии рассматриваемой системы.
За некоторый промежуток времени ∆t при силе тока I через поперечное сечение
проводника протекает электрический заряд ∆q = I∆t . Электрическое поле при этом
совершает работу
A = U∆q = UI∆t .
(1)
Используя закон Ома это выражение также можно записать в виде
U2
2
A = UI∆t = I R∆t =
∆t .
(2)
R
Как известно, работа, совершаемая в единицу времени, называется мощностью, поэтому
мощность электрического тока рассчитывается по формулам
A
U2
P=
= UI = I 2 R =
.
(3)
∆t
R
Если единственной причиной электрического сопротивления являются неупругие
столкновения заряженных частиц с частицами окружающей среды, то работа
электрического поля по поддержанию электрического тока равна количеству теплоты,
выделяющемуся в проводнике при прохождении электрического тока
189
U2
∆t .
(4)
R
Эти соотношения выражают закон Джоуля-Ленца, открытый экспериментально
английским физиком Джеймсом Джоулем и русским физиком Эмилем Ленцом.
Подчеркнем, что формулы для работы и мощности тока (2) и (3) справедливы в любом
случае при любом действии электрического тока (тепловом, механическом, химическом и
т.д.).
Q = UI∆t = I 2 R∆t =
11. 4 Электрическое сопротивление.
Если для участка цепи выполняется закон Ома, то коэффициент
пропорциональности между приложенным напряжением и силой тока ( U = RI )
называется электрическим сопротивлением участка. Электрическое сопротивление
зависит от материала проводника, его формы и размеров. Единицей измерения
электрического сопротивления в Международной системе единиц СИ является Ом сопротивление участка проводника, в котором при напряжении в 1 Вольт возникает
электрический ток силой 1 Ампер:
[1 Ом] = [1 В] .
[1 А]
Электропроводящие свойства веществ характеризуются их удельным электрически
сопротивлением ρ . Из формулы (6) предыдущего раздела следует, что размерностью
[R] ⋅ [S ] = Ом ⋅ м . Величины
удельного электрического сопротивления является [ρ ] =
[l ]
удельных сопротивлений различных веществ чаще всего определяются экспериментально
и
приводятся в физических справочниках. Для различных веществ удельное
электрическое сопротивление может изменяться в очень широких пределах. Так среди
чистых металлов наилучшими проводниками являются серебро ( ρ ≈ 1,6 ⋅ 10 −8 Ом ⋅ м ), медь
( ρ ≈ 1,7 ⋅ 10 −8 Ом ⋅ м ), алюминий ( ρ ≈ 2,8 ⋅ 10 −8 Ом ⋅ м ). В некоторых приборах (например,
электронагревательных) используются сплавы, обладающие гораздо большим удельным
сопротивлением, например,
нихром ( ρ ≈ 1,1 ⋅ 10 −6 Ом ⋅ м ). Строго говоря, между
проводниками и изоляторами нет резкой грани, все вещества (в том числе и те которые
относятся к изоляторам) в той или иной степени проводят электрический ток. Для
изоляторов удельной электрическое сопротивление велико, например, для различных
типов стекол удельное электрическое сопротивление лежит в пределах
ρ ≈ 10 9 − 1013 Ом ⋅ м , для воздуха ρ ≈ 1015 − 1018 Ом ⋅ м .
Обратите внимание – в приведенных примерах диапазон изменения удельного
сопротивления – 26 порядков!
К настоящему времени теории строения вещества разработаны достаточно глубоко, в рамках этих
теорий удается рассчитывать такую важную характеристику, как удельной сопротивление. Так даже в
рассмотренных нами элементарных моделях макроскопическая характеристика - удельное электрическое
сопротивление - выражается через микроскопические параметры.
Приведенные табличные данные являются приближенными, так как удельное
электрическое сопротивление может заметно изменяться при наличии крайне
незначительных примесей.
Кроме того, электрическое сопротивление всех веществ зависит от температуры.
Так для металлов
удельное электрическое сопротивление возрастает с ростом
температуры. Механизм этого явления достаточно сложный, мы рассмотрим его в ходе
изучения физических теорий строения веществ. Заметим, что имеются вещества (графит,
полупроводники, некоторые растворы электролитов) для которых электрическое
сопротивление уменьшается при возрастании температуры.
190
Для большинства металлов удельное электрическое сопротивление в небольшом
диапазоне температур (естественно, не включающем точку плавления) зависит от
температуры линейно, то есть может быть описано формулой
ρ = ρ 0 (1 + αt °) ,
(1)
где t ° - температура вещества, измеренная в градусах Цельсия, ρ 0 - удельное
электрическое сопротивление, α - температурный коэффициент электрического
сопротивления, равный относительному изменению сопротивления при изменении
температуры на 1° . Температурный коэффициент электрического сопротивления так же
является «индивидуальной»
характеристикой веществ, он также определяется
экспериментально. Так, например, для серебра, меди, алюминия он приблизительно равен
α ≈ 4 ⋅ 10 −3 °C −1 . В некоторых случаях необходимы вещества, для которых сопротивление
слабо зависит от температуры, так, например, для такого сплава как константан4
α ≈ 5 ⋅ 10 −5 °C −1 , что почти в сто раз меньше аналогичного показателя для меди и
алюминия.
В 1911 году голландским физиком было открыто явления сверхпроводимости. При очень низких
температурах электрическое сопротивление металлов скачком падает до нуля. Температуры перехода в
сверхпроводящее состояние различны для различных материалов, так для первого сверхпроводника,
открытого Г. Камерлинг-Оннесом, ртути эта температура составляет всего 4° K . Теория этого явления
чрезвычайно сложна и была построена только через пятьдесят лет после его открытия.
Электрическое сопротивление проводника зависит не только от материала, но и от
его размеров и формы. Широко известна полученная нами формула для расчета
сопротивления
l
R=ρ ,
(2)
S
где l - длина проводника, S - площадь его поперечного сечения.
Однако ее использование допустимо только при выполнении дополнительных условий:
1. Ток в проводнике должен быть постоянным (или изменяющимся медленно, в некотором
смысле), так как закон Ома описывает только установившейся режим протекания тока.
2. Плотность тока должна быть постоянна в поперечном сечении проводника, в противном
случае связь силой плотностью тока более сложная.
3. Длина проводника l должна быть измерена в направлении движения тока, а площадь
S в плоскости, перпендикулярной вектору плотности тока.
Пренебрежение или незнание этих дополнительных условий может приводить к курьезным
ситуациям. Так попробуйте ответить на вопрос: «Чему равно электрическое сопротивление прямоугольного
параллелепипеда изготовленного из материала с удельным электрическим сопротивлением ρ , размеры
которого равны a × b × c ?» Без указания направления распространения тока этот вопрос бессмысленный!
В общем случае для расчета сопротивления необходимо знать распределение токов
внутри проводника.
Задание для самостоятельной работы.
1. Выразите единицу электрического сопротивления Ом через основные единицы
системы СИ.
2. Найдите размерность произведения (RC ) электрической емкости и электрического
сопротивления (Фарад на Ом).
4
Само название этого сплава означает постоянный, то есть его сопротивление практически не зависит от
температуры.
191
11.5 Последовательное соединение резисторов.
При использовании электрического тока применятся электрические цепи,
различные устройства которых обладают различными электрическими свойствами.
Расчеты распределения токов и напряжений в таких цепях играет важную роль при
конструировании разнообразных приборов, потребляющих энергию электрического тока.
Реально электрическим сопротивлением обладают все проводники, то есть
электрическое сопротивление распределено по всей электрической цепи. Однако во
многих случаях удобно мысленно сосредоточить электрическое сопротивление на какомто элементе цепи, считая, что остальные участки являются идеальными проводниками.
Более того, во многих случаях электрические цепи содержат элементы, электрическое
сопротивление которых заметно превышает сопротивления подводящих проводов. Такие
элементы цепи называются резисторами.
На
электрических
схемах
резисторы
обозначаются общепринятым знаком (рис. 275), иногда
в устройствах используются резисторы, сопротивление
которых можно изменять, такие элементы называются
переменными резисторами и обозначаются на схемах,
как показано на рис. 275.
Промышленностью производятся различные типы резисторов, сопротивления которых изменяются
в широких пределах от нескольких Ом, до миллионов Ом - Мегаом ( 1 МОм = 10 Ом ). Конструктивно,
в качестве проводящего элемента используется либо проволока (проволочные резисторы), либо напыленные
на поверхность керамики слои различных материалов. Важной характеристикой резисторов является
максимальная мощность тока, который можно пропустить через резистор без его разрушения.
6
Пусть n резисторов
соединены последовательно,
то есть электрический ток
первоначально
полностью
протекает
через
один
резистор, затем через второй,
затем третий и т.д. (рис. 276)
Обозначим
сопротивления
резисторов R1 , R2 ,...Rn , напряжения на них U 1 ,U 2 ,...U n , силы токов через резисторы
I 1 , I 2 ,...I n .
Обратите внимание на правильное использование терминов: напряжение (разность потенциалов)
определяется только между двумя точками, поэтому говорят: «напряжение на таком то элементе»; сила тока
определяется для поперечного сечения проводника, для конкретной точки цепи, поэтому говорят: «сила тока
через такой-то элемент».
Суммарное напряжение на всех элементах (то есть разность потенциалов между
крайними точками цепи) назовем общим напряжением и обозначим U об . , силу тока на
входе (и выходе) рассматриваемой цепи обозначим общим I об . . По определению, общим
сопротивлением цепи на основании закона Ома назовем отношение общего напряжения к
общей силе тока
U
Rоб . = об . .
(1)
I об .
Для расчета общего сопротивления рассматриваемой цепи необходимо использовать
сформулированные законы.
По определению напряжения, как работы электрического поля, общее напряжение
равно сумме напряжений на всех элементах данной цепи. Действительно, электрические
заряды последовательно проходят через все элементы цепи, поэтому работа по
перенесению заряда через всю цепь равна сумме работ, по перенесению заряда через
каждый резистор:
192
U об . = U 1 + U 2 + ... + U n .
(2)
Далее, на основании закона сохранения электрического заряда, следует признать, что
силы токов через все резисторы одинаковы. Действительно, электрический заряд,
прошедший через первый резистор должен пройти через второй и т.д.: заряд не может
появиться и не может исчезнуть, поэтому
I об . = I 1 = I 2 = ... = I n .
(3)
Разделив равенство (2) на постоянное значение силы тока в цепи и, используя закон
Ома для каждого резистора, получим известное правило: при последовательном
соединении резисторов общее сопротивление цепи равно сумме сопротивлений всех
элементов цепи
Rоб . = R1 + R2 + ... + Rn .
(4)
В частном случае, когда n одинаковых резисторов, сопротивлением R каждый,
соединены последовательно, то общее сопротивление цепи равно Rоб . = nR
Заметим, что если в качестве резисторов используются куски одинаковой проволоки, различной
длины, то полученное правило равносильно утверждению, что общая длина всех кусков равна сумме длин
отдельных кусков.
11.6 Параллельное соединение резисторов.
При параллельном соединении электрический ток разветвляется, одновременно
проходя через все элементы цепи. Можно также сказать, что входные точки всех
параллельно соединенных резисторов соединены, также соединены их выходные точки.
Найдем общее сопротивление цепи, состоящей из
n , параллельно соединенных резисторов (рис. 277).
Обозначения сопротивлений, сил токов и напряжений
оставим прежними. На основании закона сохранения
электрического заряда можно утверждать, что общая сила
тока равна сумме токов, протекающих через все резисторы
I об . = I 1 + I 2 + ... + I n .
(5)
Электрическое поле является потенциальным, поэтому
разности потенциалов (напряжения) между концами всех
резисторов одинаковы и равны общему напряжения на
концах цепи
U об . = U 1 = U 2 = ... = U n .
(6)
Разделим равенство (5) на равное напряжение и с
помощью закона Ома получим
1
1
1
1
=
+
+ ... +
.
(7)
Rоб . R1 R2
Rn
Величина обратная сопротивлению называется
проводимостью, поэтому правило расчета параллельной цепи формулируется следующим
образом: общая проводимость параллельно соединенной цепи равна сумме
проводимостей всех элементов цепи.
В частном случае, когда n одинаковых резисторов, сопротивлением R каждый,
R
соединены параллельно, то общее сопротивление цепи равно Rоб . = .
n
Заметим, что если в качестве резисторов используются куски проволоки, из одного материала,
одинаковой длины, то полученное правило равносильно утверждению, что общая площадь поперечного
сечения всех кусков равна сумме площадей сечения отдельных кусков.
193
11.7 Примеры расчета сопротивлений цепи.
Пользуясь полученными правилами расчета последовательного и параллельного
соединения, можно рассчитать сопротивление сложной цепи, содержащей резисторы,
соединенные различными комбинированными способами. Для этого необходимо
последовательно заменять участки цепи (последовательного, параллельного соединения)
эквивалентными сопротивлениями.
Подчеркнем, что вид соединения определяется порядком протекания
электрического тока, а не тем как элементы расположены в том или ином приборе, и тем
более не тем, как они изображены на схеме. Так два резистора, показанные на рис.
соединены последовательно, а не перпендикулярно!
Рассмотрим несколько примеров расчета сопротивлений
разветвленных цепей.
Рассчитаем сопротивление цепи, изображенной на
рисунке 279. Для упрощения расчетов и экономии места
положим, что сопротивления всех резисторов одинаковы и
равны R .
Будем шаг за шагом упрощать схему, заменяя ее
части эквивалентными сопротивлениями (Рис 280).
Резисторы R2 и R3 соединены параллельно, поэтому их общее сопротивление
1
равно R23 = R (рис. 280а); резисторы R1 и R23 соединены последовательно,
2
1
3
следовательно, их сопротивление R123 = R1 + R23 = R + R = R (рис. 280б); для расчета
2
2
параллельно соединенных резисторов R123 и R4 (рис. 280 в) воспользуемся формулой
3
R⋅R
R123 ⋅ R4
3
2
R1234 =
=
= R;
R123 + R4 3 R + R 5
2
наконец, этот резистор последовательно соединен с резистором R5 , поэтому общее
3
8
сопротивление исходной цепи равно Rоб . = R1234 + R5 = R + R = R .
5
5
Рассмотрим
теперь
две
схемы, изображенные на рисунке
281.
Элементарные
расчеты,
которые можно провести в уме,
приводят
к
результату:
сопротивления обеих цепей равны
R.
194
Зададимся вопросом, является ли это совпадение случайным?
Схема а, превращается в схему б, если соединить проводником
точки А и В (рис. 282). Однако из симметрии схемы следует,
что электрический ток по этому проводнику АВ не пойдет.
Действительно, в какую сторону ему идти? – оба направления
равноправны. Еще одним доказательством отсутствия тока в
этом проводнике является равенство потенциалов точек А и В.
Рассмотрим общую схему такого соединения с
произвольными значениями сопротивлений резисторов (рис.
283) и вычислим потенциалы точек А и В. Сила тока через
R1
и
R2
последовательно соединенные резисторы
определяется законом Ома
ϕ − ϕ1
.
I1 = 0
R1 + R2
Разность потенциалов на резисторе R1 равна
ϕ − ϕ1
ϕ 0 − ϕ A = I 1 R1 = 0
R1 ,
R1 + R2
поэтому потенциал точки А равен
ϕ − ϕ1
ϕ A = ϕ0 − 0
R1 .
R1 + R2
Аналогичные рассуждения для нижней ветви цепи позволяют записать потенциал
точки В
ϕ − ϕ1
ϕB = ϕ0 − 0
R3 .
R3 + R4
Итак, условие отсутствия тока между точками А и В при их соединении точек, следующее
из равенства потенциалов ϕ A = ϕ B , имеет вид
R3
R1
R1 R3
=
=
, или
.
(1)
R1 + R2 R3 + R4
R2 R4
Рассмотренная схема называется мостиком Уитсона, а условия (1) – условием
уравновешенности (или сбалансированности) моста.
Подобные схемы широко
используются в различных электроизмерительных устройствах.
Простейший пример такого использования показа
на
рис. 284. Кусок однородной проволоки (1-2) с
достаточно высоким удельным сопротивлением натянут
на измерительную линейку, параллельно ей подключают
два резистора, сопротивление одного из них R0 известно,
сопротивление второго Rx измеряется. К образованной
таким образом мостовой схеме подключается источник
тока. К точке соединения резисторов А, подключен
чувствительный гальванометр5, второй вывод которого с
помощью скользящего контакта В подключается к проволоке. Передвигая контакт по
проволоке, добиваются того, чтобы ток через гальванометр прекратился. В этом случае
мот оказывается уравновешенным. Так как сопротивление проволоки пропорционально ее
длине, то условие уравновешенности (1) в данном случае имеет вид
Rx l 2
= ,
R0 l1
5
Гальванометр – индикаторный прибор, задача которого показывать наличие даже малых токов.
195
из которого легко определить неизвестное сопротивление, по измерению длин частей
проволоки. В данной схеме электрическое сопротивление измеряется, фактически, с
помощью линейки. Помимо простоты данной схемы, ее достоинством является отсутствие
необходимости измерять значение силы тока, достаточно убедится в его отсутствии, что
может быть сделано с высокой точностью. Подобный метод измерения называется
«нулевым».
В некоторых случаях точки цепи, имеющие одинаковый потенциал, определяются
просто, исходя из симметрии схемы. В таких ситуациях расчет электрического
сопротивления значительно упрощается: во-первых, если такими точками включены
элементы цепи, то их можно отбросить, так как электрический ток через них не течет; вовторых, точки равного потенциала можно соединить проводником – это не приведет к
изменению сопротивления, так как распределение токов в цепи не изменится.
Рассчитаем, например, сопротивление каркасного октаэдра6, изготовленного из
проволоки, сопротивление каждого ребра которого равно R (рис.
285). При подключении источника тока к противоположным
вершинам А и В, точки 1,2,3,4 равноправны, поэтому имеют
одинаковый потенциал. Следовательно, ток не течет по ребрам
октаэдра, соединяющим эти вершины, поэтому, их можно отбросить,
не нарушая распределения токов по остальным ребрам. Тогда
сопротивление каркаса становится эквивалентным сопротивлению
четырех параллельно соединенных ветвей, состоящих из двух ребер,
общее сопротивление равно R .
2
Найдем сопротивление проволочного куба, сопротивление
каждого ребра которого равно R , при подключении источника тока к
противоположным вершинам А и В (рис. 286). Вершины куба 2,4,5
находятся на расстоянии одного ребра от точки «входа» А, поэтому
их потенциалы равны, следовательно, их можно соединить между
собой, не нарушая при этом распределения токов по ребрам куба.
Аналогично, можно соединить между собой вершины 3,6,8. Таким
образом, точка А оказывается соединенной с «объединенной точкой
2 ,4,5» тремя параллельно соединенными ребрами, от «точки 2 ,4,5»
до «точки 3,6,8» включено параллельно шесть ребер, и
далее до выхода, точки В, еще три параллельно соединенных
ребра. Таким образом, получаем эквивалентную схему
рассматриваемого каркаса (рис. 287), общее сопротивление
которой рассчитывается элементарно
R R R 5
Rоб . = + + = R .
3 6 3 6
11.8 Электрическое сопротивление среды при пространственно распределенных
токах.
Электрический ток может протекать не только «концентрировано», по проводам.
Движение электрических зарядов можетr занимать определенную область проводника, при
этом векторное поле плотности тока j ( x, y, z ) , не обязательно является однородным, а
представлять достаточно сложную структуру. Расчет электрического сопротивления
между различными точками среды в этом случае принципиально отличается от
рассмотренных выше. Особо отметим, что электрическое сопротивление среды зависит не
только от ее свойств (удельного электрического сопротивления), но и от распределения
6
Октаэдр – один из пяти правильных многогранников, образованный восьмью правильными
треугольниками.
196
токов в среде. Проиллюстрируем это положения двумя примерами, заодно и покажем
методы расчета сопротивления для пространственно распределенных токов.
Пример 1. Пространство между двумя концентрическими
хорошо проводящими сферами радиусами r1 и r2 заполнено
слабопроводящим веществом с удельным электрическим
сопротивлением ρ (рис. 288). Определим сопротивление
среды между сферами.
Оговорки о проводимости сфер и среды между ними
позволяют использовать следующие приближения:
- считать потенциалы сфер постоянными и пренебречь их
сопротивлением;
- пренебречь объемными зарядами в пространстве между
сферами, которые, в принципе, могут возникать при
протекании электрического тока.
Для расчета сопротивления среды между сферами положим, что на внутренней
сфере поддерживается постоянный электрический заряд + q (то есть сфера подключена к
источнику тока, который компенсирует заряд, стекающий с него через проводящую
среду). Электрическое поле в пространстве между сферами эквивалентно полю точечного
заряда + q , помещенного в центр сфер. Следовательно, разность потенциалов между
сферами может быть рассчитана по знакомой из электростатики формуле
q ⎛1 1⎞
⎜ − ⎟.
(1)
∆ϕ =
4πε 0 ⎜⎝ r1 r2 ⎟⎠
Так как
r система обладает сферической симметрией, то вектор плотности электрического
тока j во всех точках направлен радиально (вдоль прямой проходящей через центр сфер).
Задание для самостоятельной работы.
1. Докажите, что модуль вектора плотности тока убывает обратно пропорционально
квадрату расстояния до центра сфер.
Непосредственно у поверхности внутренней сферы напряженность электрического поля
равна
q
E=
.
(2)
4πε 0 r12
По закону Ома плотность тока у поверхности сферы равна
1
q
j= E=
.
(3)
ρ
4πε 0 ρr12
Так как вектор плотности тока направлен радиально, то есть по нормали к поверхности
сферы, и постоянен по модулю, то сила электрического тока, стекающего со сферы,
равная потоку вектора плотности тока, равна произведению плотности тока на площадь
q
q
⋅ 4πr12 =
. Зная силу тока и разность потенциала,
сферы I = jS =
2
ε0ρ
4πε 0 ρr1
электрическое сопротивление рассматриваемой системы определим по закону Ома
ρ ⎛ 1 1 ⎞ ρ (r2 − r1 )
∆ϕ
⎜ − ⎟=
.
(4)
R=
=
I
4π ⎜⎝ r1 r2 ⎟⎠
4πr2 r1
Как и следовало ожидать, полученное значение сопротивления не зависит от
«придуманного» заряда внутренней сферы.
197
Итак, суть использованного метода сводится к независимому расчету разности
потенциалов и силы тока между сферами, при заданном значении заряда сферы. Величина
этого заряда сокращается при вычислении сопротивления.
Интересно отметить, что если расстояние между сферами ∆r = (r2 − r1 ) значительно меньше их
радиусов, то в знаменателе формулы (4) можно пренебречь различием в их радиусах, тогда знаменатель
упрощается 4πr2 r1 ≈ 4πr = S , то есть становится равным площади поверхности сферы. В этом случае
2
полученная формула (4) превращается в банальную R =
ρ
l
.
S
1
→ 0 ), то
r2
рассматриваемая система превращается в заряженный шарик, помещенный в бесконечную
проводящую среду. В этом случае сопротивление среды от шарика радиуса r до
«бесконечности» оказывается равным
Если радиус внешней сферы устремить к бесконечности ( r2 → ∞,
R=
ρ
.
4πr
(5)
Пример 2. Два одинаковых металлических
шарика, радиусы которых равны r , находятся
на большом расстоянии a ( a >> r ) друг от
друга в слабопроводящей среде с удельным
электрическим сопротивлением ρ (рис. 289).
Вычислим
электрическое
сопротивление
среды между шариками.
Для
расчета
электрического
сопротивления мысленно сообщим шарикам
электрические заряды, равные по величине и
противоположные по знаку (+ q,− q ) . Так расстояние между шариками значительно
больше размеров шарика, то можно пренебречь влиянием заряда одного шарика
потенциал другого, тогда разность потенциалов между шариками определяется по
формуле
(+ q ) − (− q ) = q ,
∆ϕ = ϕ + − ϕ − =
(6)
4πε 0 r 4πε 0 r 2πε 0 r
где ϕ + , ϕ − - потенциалы положительно и отрицательно заряженных шариков,
соответственно.
Распределение напряженности электрического поля (и соответствующей ему
плотности тока) в данном случае достаточно сложной7. Однако для вычисления силы тока,
стекающего с одного из шариков, знание его не требуется. Мысленно окружим
положительно заряженный шарик произвольной замкнутой поверхностью Ω . Поток
вектора плотности тока через эту поверхность и будет равен суммарной силе тока между
шариками I = Φ rj . По закону Ома плотность тока пропорциональна напряженности
r 1 r
электрического поля j = E ; так как поток пропорционален этому вектора, то такое же
ρ
соотношение будет выполняться и для потоков векторов плотности тока и напряженности
1
поля Φ rj = Φ Er . Для потока вектора напряженности электрического поля справедлива
ρ
7
Оно соответствует полю двух точечных зарядов, рассмотренному и нарисованному ранее.
198
теорема Гаусса Φ Er =
q
ε0
. Таким образом, сила тока между шариками
выражается
элементарно
I = Φ rj =
1
ρ
Φ Er =
q
ρε 0
Теперь легко вычислить искомое сопротивление
ρ
∆ϕ
R=
=
.
I
2πr
.
(7)
(8)
Задания для самостоятельной работы.
1. В каком месте при выводе формулы (8) мы учли, что ток идет между шариками?
2. Получите более точную формулу для сопротивления между шариками с учетом
расстояния между ними (не полагая его бесконечно большим).
Теперь, внимание! Сравним два результата, формулы (5) и (8) – сопротивления,
рассчитанные по этим формулам, отличаются в два раза, хотя, и в одном и другом случае
рассматривается стекание тока с металлического шарика в неограниченную среду.
Причина такого существенного расхождения заключается в различной структуре поля
электрических токов – если в первом случае ток растекается радиально, одинаково во все
стороны, то во втором ток преимущественно направлен в одну сторону, ко второму
шарику. Тем самым, мы наглядно продемонстрировали, что электрическое сопротивление
зависит не только от свойств среды и размеров источника, но и распределением токов.
11.9 Время установления стационарного тока.
В окружающем мире ничто не происходит мгновенно – всякому стационарному
процессу предшествует процесс установления, имеющий конечную длительность. Оценка
характерных времен установления стационарного режима необходима для анализа
применимости различных упрощающих моделей, в частности стационарных. Процессы
перехода в стационарный режим часто называют переходными или релаксационными.
В данном разделе мы обсудим некоторые факторы, влияющие и определяющие
длительность таких процессов для электрического тока.
Время распространения электрического поля определяется скоростью света и
размерами рассматриваемой электрической цепи. Мы уже отмечали, что при
подключении проводящей цепи к источнику первоначально проходит процесс
распространения электрического поля вдоль цепи. Само же электрическое поле
м
распространяется вдоль проводов со скоростью близкой к скорости света c ≈ 3 ⋅ 10 8 .
с
Поэтому время установления электрического поля вдоль цепи длиной l оценивается как
l
τ1 ≈ .
(1)
c
Так если электрическая осветительная лампочка находится на расстоянии 10 метров от
выключателя, то после его замыкания, электрическое поле достигает лампочки через
время τ ≈ 3 ⋅ 10 −8 c . Скорость света велика настолько, что если выключатель расположить
на северном полюсе Земли, а лампочку на южном, то поле достигнет лампочку через
время меньшее 0,1с (учитывая, что длина меридиана приблизительно равна
20 000км = 2 ⋅ 10 7 м ).
Закон Ома описывает установившееся движение заряженных частиц. Прежде чем
эти частицы начнут двигаться с постоянной скоростью (в среднем), они разгоняются.
Время разгона заряженных частиц определяется массой частиц и тормозящей силой.
Для оценки этого времени воспользуемся рассмотренной моделью движения электронов в
199
металле, в рамках которой считается, что на движущиеся электроны действует
тормозящая сила, пропорциональная скорости движения. В рамках этой модели уравнение
второго закона Ньютона имеет вид (с сохранением всех прежних традиционных
обозначений)
ma = eE − βv .
Движение, описываемое этим уравнением, не является ни равномерным, ни
равноускоренным. Пусть в начальный момент времени скорость электрона равна нулю
eE
v0 = 0 , тогда он начинает двигаться с ускорением a 0 =
,
m
по мере роста скорости ускорение уменьшается, наконец,
когда тормозящая сила уравновесит силу, действующую со
стороны электрического поля, ускорение обратится в нуль,
и дальнейшее движение будет проходить с постоянной
eE
установившейся скоростью v =
(рис. 290). Для оценки
β
характерного времени разгона можно принять, что
скорость нарастает с ускорением a0 от нуля до
установившегося значения, поэтому это время равно
v
m
τ2 =
= .
a0 β
(2)
Заметим, что использованный метод получения оценок является традиционным для многих подобных задач.
Модельный параметр β выражается через характеристики проводника посредством
формулы для удельного электрического сопротивления, полученной нами ранее
2m
β
ρ= 2 = 2 .
(3)
e nτ e n
Таким образом, время разгона электронов в металле оценивается формулой
m
m
τ2 ≈ ≈ 2 .
(4)
β e nρ
Обратите внимание, что полученный результат не зависит от напряженности
электрического поля, действующего на электрон. Так для меди (концентрация свободных
электронов для которой n ≈ 8 ⋅ 10 28 м −3 , а ρ ≈ 1,7 ⋅ 10 −8 Ом ⋅ м ) время разгона равно
τ2 ≈
9 ⋅ 10 −31 кг
≈ 3 ⋅ 10 −14 с .
(5)
Кл ) ⋅ 8 ⋅ 10 м ⋅ 1,7 ⋅ 10 Ом ⋅ м
Полученное время настолько мало, что экспериментально его зарегистрировать
невозможно, поэтому временем разгона электронов практически всегда можно
пренебречь. Малость полученного времени во многом обусловлена малостью массы
электрона.
(1,6 ⋅10
−19
2
28
3
−8
Для наглядного представления о полученной длительности укажем, что
времени свет проходит расстояние порядка 10
волоса.
−7
за такой промежуток
м , которое приблизительно равно толщине человеческого
Интересно отметить, что характерное время разгона по порядку величины
совпадает со средним временем свободного движения электрона между столкновениями.
2m
Это время легко выразить из формулы (3) τ = 2
.
e nρ
Задания для самостоятельной работы.
1. Оцените время разгона иона Na + в 10% растворе поваренной соли в воде. Удельное
электрическое сопротивление такого раствора приблизительно равно ρ ≈ 8 ⋅ 10 −2 Ом ⋅ м .
200
2. Из формулы (4) следует, что для сверхпроводников (для которых ρ = 0 ) время разгона
электронов стремится к бесконечности. Объясните данный результат.
Изучив основные законы движения заряженных частиц в веществе, можно оценить
применимость электростатических моделей. Так, при изучении поведения веществ в
электрическом поле, мы говорили, что в проводниках очень быстро устанавливается
равновесное распределение индуцированных зарядов на его поверхности. Диэлектриками
мы назвали вещества, которые не проводят электрический ток. Однако все вещества в той
или иной степени проводят электрический ток, поэтому граница между проводниками и
диэлектриками условна. Сейчас мы можем дать количественный критерий возможности
использования моделей идеальных проводников (веществ, электрическим сопротивлением
можно пренебречь) и идеальных диэлектриков (веществ, проводимостью которых можно
пренебречь). Для этого нам необходимо оценить время установления равновесного
распределения индуцированных зарядов.
Для этого рассмотрим следующую систему: пространство между
двумя параллельными хорошо проводящими пластинами заполнено
однородным веществом с удельным электрическим сопротивлением ρ
(рис. 291), то есть представляет собой обыкновенный плоский
конденсатор. Пусть в начальный момент времени на пластинах
равномерно распределены электрические заряды с поверхностными
плотностями + σ и − σ . Оценим время, за которое конденсатор
разрядится, то есть электрические заряды
перетекут через слой
вещества. Пренебрегая диэлектрическими свойствами заполняющего
вещества, напряженность однородного электрического поля внутри конденсатора может
быть описана формулой E =
σ
, тогда по закону Ома плотность электрического тока
ε0
будет равна
j=
1
ρ
E=
σ
.
ε0ρ
(6)
Выделим в конденсаторе небольшой цилиндр, основания которого лежат на пластинах и
имеют площадь ∆S . Сила электрического тока, протекающего по цилиндру равна
I = j∆S =
σ
∆S . Этот ток равен скорости уменьшения электрического заряда q = σ∆S
ε0ρ
на основаниях цилиндра. Поэтому изменение поверхностной плотности заряда
описывается уравнением
∆q
∆σ
σ
= − I , или
=−
.
∆t
∆t
ε0ρ
(7)
Как следует из этого уравнения, скорость уменьшения
заряда пропорциональна поверхностной плотности
заряда. Поэтому в начальный момент времени, когда
плотность
заряда
σ 0 максимальна,
скорость
уменьшения заряда также максимальна и равна
σ
⎛ ∆σ ⎞
j0 = ⎜
⎟ = − 0 . Далее по мере уменьшения
ε0ρ
⎝ ∆t ⎠ 0
зарядов на пластинах, скорость разрядки (равная
плотности тока) будет уменьшаться (см. рис. 292). Оценку характерного времени
разрядки можно получить, полагая, что поверхностная плотность уменьшается от σ 0 до
201
j 0 . Таким образом, получаем интересующее нас
нуля с постоянной скоростью разрядки
время
τ3 =
σ0
j0
= ε0ρ .
(8)
Эта важная формула может быть получена и в более общем случае. Предположим, что внутри
большого тела, изготовленного из однородного вещества с удельным
электрическим сопротивлением ρ возникла малая область, имеющая
электрический заряд q (рис. 293). Уменьшение заряда этой области
связано с его растеканием по всему объему тела. Окружим
рассматриваемую заряженную область замкнутой поверхностью Ω .
Сила электрического тока пересекающего через эту поверхность,
равна скорости уменьшения заряда внутри поверхности. Эта сила
тока равна потоку вектора плотности тока через поверхность
I = Φ rj . Так как по закону Ома плотность тока пропорциональна
напряженности электрического поля
r 1 r
j = E , то потоки этих
ρ
векторов связаны аналогичным соотношением Φ rj =
поля определяется теоремой Гаусса Φ Er =
области подчиняется уравнению
q
ε0
1
ρ
Φ Er . Поток вектора напряженности электрического
. Таким образом, величина заряда внутри рассматриваемой
∆q
1
q
= − I = −Φ rj = − Φ Er = −
,
∆t
ρ
ρε 0
которое полностью совпадает с уравнением
формулой (8).
(7), поэтому время растекания заряда также оценивается
Полученная нами оценка времени установления зарядов на проводнике называется8
максвелловским временем релаксации. Мы уже указывали, что удельные
электрические сопротивления веществ изменяются в очень широких пределах,
соответственно изменяются и времена установления зарядов на них. Так для хороших
проводников, например меди, это время равно
Ф
τ 3 = 1,7 ⋅ 10 −8 Ом ⋅ м ⋅ 8,85 ⋅ 10 −12 ≈ 1,5 ⋅ 10 −19 с .
м
Это время чрезвычайно мало, поэтому для таких вещества при описании
электростатических явлений с высокой степенью точности можно считать идеальными
проводниками.
В качестве противоположного примера (изолятора) возьмем широко известный
полиэтилен, для которого ρ ≈ 1015 Ом ⋅ м , соответственно, максвелловское время
Ф
релаксации τ 3 = 1015 Ом ⋅ м ⋅ 8,85 ⋅ 10 −12 ≈ 10 4 с ≈ 3 час . Поэтому если вам необходимо
м
рассматривать процессы, протекающие в полиэтилене в течение нескольких минут, то с
высокой степенью точности полиэтилен можно считать идеальным диэлектриком
(изолятором). Для веществ, имеющих удельное сопротивление порядка 1011 − 1012 Ом ⋅ м
(сухая древесина, резина, некоторые виды стекол и пластмасс), максвелловское время
составляет от десятых долей секунды до нескольких секунд.
Таким образом, относить вещество к проводникам или изоляторам, можно только при
учете характерных времен протекающих электрических процессов: если эти времена
значительно меньше τ 3 = ε 0 ρ , то вещество можно отнести к диэлектрикам, если же
времена процессов значительно больше времени релаксации, то вещество следует считать
8
В честь английского физика Дж. К. Максвелла, впервые получившего эту формулу в середине XIX века.
202
диэлектриком. Действительно, для быстрых процессов, перемещением зарядов внутри
вещества можно пренебречь.
Так, например, если внутри рассмотренного конденсатора находится деревянная
дощечка ( ρ ≈ 1010 Ом ⋅ м , τ 3 ≈ 0,1 с ), то при включении его в цепь переменного тока с
частотой порядка9 10 3 c −1 (тысяча колебаний в секунду, период колебания 0дна тысячная
секунды) древесину можно считать идеальных диэлектриком. Если этот конденсатор
зарядить, то он разрядится через одну десятую долю секунды, то есть через этот
промежуток времени древесину можно считать проводником (но, конечно, не идеальным).
Итак, мы рассмотрели некоторые процессы, определяющие времена установления тока и
распределения зарядов на проводнике. Сразу оговоримся, что мы рассмотрели не все явления, влияющие на
переходные процессы в электрических цепях. Еще одним из важнейших процессов подобного рода является
возникновение магнитного поля при протекании электрического тока. С ним познакомимся позднее, при
изучении свойств магнитного поля.
9
Для современных технологий очень малая частота – компьютеры работаю на частотах превышающих
1ГГц = 109 с −1
203
11.10 Условия существования постоянного электрического тока в цепи.
Обсудим, при каких общих условиях можно создать устройство, в котором
длительное время может существовать электрический ток.
Первое обязательное условие – наличие проводников, так как заряженные
частицы могут двигаться только в проводниках. Если
проводящее тело поместить в электрическое поле, то под его
действием свободные заряженные частицы придут в
движения, то есть появится электрический ток (рис. 294).
Однако движение этих частиц приведет к появлению
индуцированных зарядов, которые, в свою очередь, приведет к
возникновению электрического поля, которое полностью
компенсирует внешнее поле, поэтому электрический ток
прекратится очень быстро. Следовательно, для поддержания
электрического тока в проводнике необходимо постоянно
переносить заряды с одной стороны проводника на другую.
Иными словами необходимо создать замкнутый проводящий контур, по которому
может циркулировать постоянный ток. Обязательность наличия замкнутого контура также
обосновывается законом сохранения электрического заряда. Для того чтобы переносить
заряды с одной стороны рассматриваемого проводника на другую необходимо постоянно
совершать работу против сил электрического поля. То есть в контур необходимо
включить устройство, совершающее эту работу. Сразу заметим, что указанная работа не
может быть совершена электростатическим полем! Так как электростатическое поле
потенциально, то работа сил пол по перемещению зарядов по любому замкнутому контура
равна нулю. Поэтому попытки придумать такое расположение зарядов, которая создает
электростатическое поле, обеспечивающее существование постоянного тока, обречены на
неудачу. Следовательно, упомянутое устройство для переноса зарядов против сил
электростатического поля (назовем его источником или генератором тока), должно
переносить заряды с помощью любых сил, кроме электростатических. Сторонние силы не
должны быть потенциальными, так работа этих сил по замкнутому контуру должна быть
положительна, то есть, отлична от нуля.
Можно также говорить, что источник тока должен разделять электрические заряды,
перенося заряды одного знака на один полюс источника, а заряды другого знака на
второй. При появлении зарядов на полюсах источника внутри его создается электрическое
поле, чтобы продолжить разделение зарядов необходимо совершать работу по
преодолению сил этого поля.
Силы, совершающие работу по перенесению электрических зарядов против
сил электростатического поля, называются сторонними силами. Природа сторонних
сил может быть самой различной, эти силы могут возникать в результате протекания
химических реакций (в гальванических элементах и аккумуляторах), они могут возникать
при изменении магнитного поля (в электромагнитных генераторах), в фотоэлементах
разделение зарядов происходит под действием света и т.д.
Здесь уместно провести аналогию с движением вязкой жидкости по трубам. Для того, чтобы
жидкость текла по трубе, к ней постоянно необходимо прикладывать внешнюю силу для преодоления сил
вязкости. В качестве такой силы может выступать, например, сила тяжести. Для поддержания постоянного
тока жидкости необходимо создать замкнутый контур, в который следует включить насос, совершающий
работу по подъему жидкости, то есть работу против сил тяжести. Таким образом, источник тока в
электрической цепи играет ту же роль, что и насос в водопроводном контуре.
11.11 Электродвижущая сила (ЭДС) и внутреннее сопротивление источника.
Мы пришли к выводу, что для поддержания постоянного тока в замкнутой цепи, в
нее необходимо включить источник тока. Подчеркнем, что задача источника заключается
не в том, чтобы поставлять заряды в электрическую цепь (в проводниках этих зарядов
достаточно), а в том, чтобы заставлять их двигаться, совершать работу по перемещению
204
зарядов против сил электрического поля. Основной характеристики источника является
электродвижущая сила1 (ЭДС) – работа, совершаемая сторонними силами по
перемещению единичного положительного заряда
A
ε = ст. .
(1)
q
Единицей измерения ЭДС в системе единиц СИ является Вольт. ЭДС источника
равна 1 вольт, если он совершает работу 1 Джоуль при перемещении заряда 1 Кулон
[1В] = [1 Дж ] .
[1Кл]
Для обозначения источников тока на электрических схемах
используется специальное обозначение (рис.295).
Электростатическое поле совершает положительную работу по
перемещению положительного заряда в направлении уменьшения потенциала поля.
Источник тока проводит разделение электрических зарядов – на одном полюсе
накапливаются положительные заряды, на другом отрицательный. Напряженность
электрического поля в источнике направлена от положительного полюса к
отрицательному, поэтому работа электрического поля по перемещению положительного
заряда будет положительной при его движения от «плюса» к «минусу». Работа сторонних
сил, наоборот, положительна в том случае, если положительные заряды перемещаются от
отрицательного полюса к положительному, то есть от «минуса» к «плюсу».
В этом принципиальное отличие понятий разности потенциалов и ЭДС, о котором
всегда необходимо помнить.
Таким образом, электродвижущую силу источника можно считать
алгебраической величиной, знак которой («плюс» или «минус») зависит от
направления тока. В схеме, показанной на рис. 296, вне источника (во
внешней цепи) ток течет2 от «плюса» источника к «минусу», в внутри
источника от «минуса» к «плюсу». В этом случае, как сторонние силы
источника, так и электростатические силы во внешней цепи совершают
положительную работу.
Если на некотором участке электрической цепи помимо
электростатических действую и сторонни силы, то над перемещением
зарядов «работают» как электростатические, так и сторонние силы. Суммарная работа
электростатических и сторонних сил по перемещению единичного положительного
заряда называется электрическим напряжением
на участке цепи
A + Aст.
U = эл.
= ϕ 0 − ϕ1 + ε .
(2)
q
В том случае, когда сторонние силы отсутствуют,
электрическое напряжение совпадает с разностью
потенциалов электрического поля.
Поясним определение напряжения и знака
ЭДС на простом примере. Пусть на участке цепи, по
которому протекает электрический ток, имеются
источник сторонних сил и резистор (рис. 297). Для
определенности будем считать, что ϕ 0 > ϕ 1 , то есть
1
Название этой физической величины неудачно – так электродвижущая сила является работой, а не силой в
обычном механическом понимании. Но этот термин настолько устоялся, что изменять его не «в наших
силах». К слову, сила тока то же не является механической силой! Не говоря уж о таких понятиях «сила
духа», «сила воли», «божественная сила» и т.д.
2
Напомним, за направление движения электрического тока принято направление движения положительных
зарядов.
205
электрический ток направлен от точки 0 к точке 1. При подключении источника, как
показано на рис. 297а, Сторонние силы источника совершают положительную работу,
поэтому соотношение (2) в этом случае может быть записано в виде
U = ϕ 0 − ϕ1 + ε .
При обратном включении источника (рис. 297б) внутри него заряды движутся против
сторонних сил, поэтому работа последних отрицательна. Фактически силы внешнего
электрического поля преодолевают сторонние силы. Следовательно, в этом случае
рассматриваемое соотношение (2) имеет вид
U = ϕ 0 − ϕ1 − ε .
Для протекания электрического тока по участку цепи, обладающему электрическим
сопротивлением, необходимо совершать работу, по преодолению сил сопротивления. Для
единичного положительного заряда эта работа, согласно закону Ома, равна произведению
IR = U которое, естественно совпадает с напряжением на данном участке.
Заряженные частицы (как электроны, так и ионы) внутри источника движутся в
некоторой окружающей среде, поэтому со стороны среду на них также действуют
тормозящие силы, которые также необходимо преодолевать. Заряженные частицы
преодолевают силы сопротивления благодаря действию сторонних сил (если ток в
источнике направлен от «плюса» к «минусу») либо благодаря электростатическим силам
(если ток направлен от «минуса» к «плюсу»). Очевидно, что работа по преодолению
этих сил не зависит от направления движения, так как силы сопротивления всегда
направлены в сторону, противоположную скорости движения частиц. Так как силы
сопротивления пропорциональны средней скорости движения частиц, то работа по их
преодолению пропорциональна скорости движения, следовательно, силе тока силе. Таким
образом, мы можем ввести еще характеристику источника – его внутренне
сопротивление r , аналогично обычному электрическому сопротивлению. Работа по
преодолению сил сопротивления при перемещении единичного положительного заряда
A
между полюсами источника равна
= Ir . Еще раз подчеркнем, эта работа не зависит от
q
направления тока в источнике.
11.12 Закон Ома для полной цепи.
Рассмотрим подробнее процессы, протекающие в замкнутой цепи электрического
тока, содержащей источник (рис. 298).
Внутри источника под действием сторонних сил начинается разделение зарядов:
положительно заряженные частицы движутся к положительному полюсу источника, а
отрицательные частицы к отрицательному. Разделенные заряды создают внутри
r
источника электрическое поле E , направленное от «плюса» к «минусу», которое
206
препятствует дальнейшему движению зарядов. Кроме того, на движущиеся заряженные
частицы действуют силы сопротивления среды Fсопр. . Чтобы заряженные частицы
продолжали двигаться, к ним должна быть приложена сторонняя сила Fст. . При
постоянном токе (в установившемся режиме) соотношение между действующими силами
очевидно – сумма сил, действующих на частицу должна быть равна нулю, или
Fст. = qE + Fсопр.
Работа сторонних сил по перемещению единичного положительного заряда, по
определению равна ЭДС источника ε . Работа сил сопротивления отрицательна и по
модулю равна произведению силы тока на внутреннее сопротивление источника Ir .
Работа сил электрического поля при движении зарядов внутри источника также
отрицательна.
При подключении внешней цепи внутри проводника возникает электрическое поле.
Механизм создания этого поля достаточно сложен. Несколько упрощенно можно сказать,
что на поверхности проводника появляются заряды, распределение которых таково, что
они создают внутри проводника такое электрическое поле3, которое поддерживает
постоянный по всей цепи электрический ток.
Подобно тому, как в электростатике индуцированные заряды и электрическое поле приходят в
равновесие, при котором прекращается движение зарядов, в случае постоянного тока наступает равновесие
несколько иного вида – постоянство электрического тока. Если в каком то месте электрический ток
превышает равновесное значение, то происходит накопление заряда, которое уменьшает электрический ток,
и наоборот при недостатке зарядов в некоторой области цепи, увеличивающийся электрический ток
компенсирует недостаток заряда.
Во внешней цепи заряженные частицы движутся под действием силы со стороны
созданного электрического поля, которая при постоянном токе равна силе сопротивления
qE = Fсопр.
Во внешней цепи работа электрического поля по перемещению зарядов
положительна (и для единичного заряда равна разности потенциалов на концах внешней
цепи), а работа сил сопротивления по-прежнему отрицательна и равна по модулю
произведению силы тока на сопротивление цепи IR .
Проследим за движением отдельной заряженной частицы по всему контуру –
совершив полный обход, эта частица возвращается в исходное состояние. Следовательно,
ее энергия также принимает начальное значение. Поэтому полная работа внешних сил,
при движении частицы по замкнутому контуру равна нулю. Во время движения на
рассматриваемую частицу действовали силы сопротивления, сторонние силы и силы
электростатического поля.
Aст. + Aсопр. + Aэл. = 0
Но, электростатическое поле всегда потенциально, поэтому работа этих сил по контуру
равна нулю – положительная работа во внешней цепи равна по модулю отрицательной
работе внутри источника Aэл. = 0 . Поэтому при движении по контуру работа сторонних
сил равна по модулю работе сил сопротивления Aст. + Aсопр. = 0 . Для единичного заряда
это утверждение выражается уравнением
ε = IR + Ir ,
из которого следует, что сила тока в цепи рассчитывается по формуле
ε
,
I=
R+r
(1)
Сила тока в замкнутом контуре цепи равна отношению ЭДС контура к полному
сопротивлению контура. Данное утверждение называется законом Г.С. Ома для полной
3
Мы не утверждаем, что напряженность этого поля равна напряженности поля внутри источника, более
того, электрические поля могут быть различны в различных точках как внутри источника, так и во внешней
цепи.
207
цепи. Фактически данный закон можно рассматривать как закон сохранения энергии для
системы движущихся зарядов. Действительно, энергия, сообщенная заряженной частице,
равна работе по преодолению сил сопротивления. Если все потери энергии частицы
обусловлены сопротивлением цепи, то указанная работа равна количеству теплоты,
выделившейся во внешней цепи и внутри источника. Если в цепи имеются приборы,
преобразующие энергию электрического тока в другие формы (механическую, световую,
химическую и т.д.), то работа источника равна сумме энергии, потребляемой этими
приборами, и количества теплоты, выделившейся в цепи – иными словами, закон
сохранения энергии не знает исключений и в данных явлениях.
208