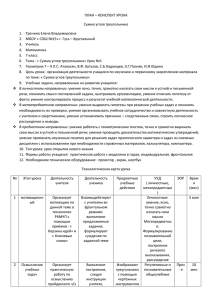
уравнению четвертой степени
реклама

Задача. На плоскости даны три луча, исходящие из одной точки. Построить равносторонний треугольник так, чтобы вершины лежали на этих лучах. Геометрическое построение искомого треугольника достаточно тривиально, но не очевидно. Здесь предлагается отыскать алгоритм построения искомого треугольника путем аналитических вычислений, сформулировав вначале соответствующую аналитическую задачу. Аналитическое решение иногда обладает некоторым преимуществом, поскольку в нем легче заметить возможные особенности задачи. Аналитическая формулировка задачи. Рассматривая рис.1 и полагая луч, совпадающим с осью абсцисс и устанавливаются координаты точки Так как координаты остальных углов треугольника и должны располагаться на прямых и исходящих из начала координат, то между координатами точек должны соблюдаться равенства где коэффициенты и совпадают с тангенсами углов наклона прямых, определенных заданными лучами. Основное свойство равностороннего треугольника, выраженное в координатах с учетом указанных равенств между координатами приводит к трем уравнениям относительно двух неизвестных и . 1. Правильный треугольник с вершинами на трех лучах Для упрощения записи уравнений удобно ввести новые термины (1) связанные между собой легко доказываемым тождеством (2) Записанная в новых терминах система (3) показывает, что одно из неизвестных можно исключить Подстановка его в последнее уравнение приводит к уравнению четвертой степени 2 относительно Попутно следует заметить, что если воспользоваться свойством равенства углов равностороннего треугольника, приводящего к равенству скалярных произведений векторов, на которых построен треугольник, то в результате возникают те же алгебраические уравнения (3). Разложение многочлена на множители. Многочлен четвертой степени всегда можно разложить на два многочлена второй степени, вследствие чего должно выполняться тождество которое выполняется, если имеет место система равенств Рассматривая последнюю как систему уравнений относительно параметров квадратных трехчленов, сразу можно заметить, что в системе из пяти уравнений имеется шесть неизвестных. Это означает, что имеется свобода выбора одного из параметров. Предоставленная свобода позволяет установить Тогда в системе остается четыре уравнения с четырьмя неизвестными Путем исключения двух неизвестных в системе остается два уравнения (4) относительно двух неизвестных и Для начала следует проверить, не являются ли рассматриваемые неизвестные, не зависящими от какого-либо из выбранных параметров или Поскольку параметр входит линейно в оба уравнения, то удобно продифференцировать обе части обоих уравнений по этому параметру. В результате рассматриваемая система упрощается и из второго уравнения становится очевидным возможные значение одного из параметров Подстановка их в первое уравнение вызывает очевидные ограничения на выбор другого параметра Следовательно, возникают три пары 3 которые следует проверить, не являются ли некоторые из них корнями исходной системы (4). Проверка показывает, что вторая пара и в действительности оказывается решением рассматриваемой системы, если учитывать свойство (2) между новыми параметрами (1). Следовательно, вычисление корней полинома четвертой степени сводится к вычислению корней двух квадратных трехчленов где параметры второго трехчлена легко вычисляются по найденному решению для первого трехчлена Исследование корней трехчленов. Дискриминант первого трехчлена отрицателен поэтому корни многочлена совпадают с корнями квадратного уравнения . Дискриминант второго трехчлена приведенный с учетом свойства (2) к виду оказывается полным квадратом что становится очевидным, если вернуться к исходным тангенсам угла наклона исходных лучей Тогда решения рассматриваемого квадратного уравнения легко вычисляются В результате для абсциссы первой точки правильного треугольника получается два значения где Поскольку оба решения оказываются рациональными функциями тангенса углов наклона лучей, то имеется возможность построить искомый равносторонний треугольник. Но прежде, чем перейти к интерпретации полученных решений, уместно попытаться упростить выражения найденных решений. Упрощение выражений Знаменатель решений удается разложить на множители, если представить его как многочлен второй степени относительно коэффициента Вычисление корней приведенного многочлена 4 приводит к очевидному разложению на множители От коэффициента при старшей степени , вносящего дополнительную особенность в решение, можно избавиться. И действительно, поскольку то рассматриваемый знаменатель становится свободным от выделенного коэффициента где Осталось представить решения, рассматриваемые как функции от параметра виде сумм простейших дробей в где параметры и легко вычисляются, если последние равенства попеременно умножить на знаменатели простейших дробей и воспользоваться после упрощения левой части подстановкой корня, обращающего одно из слагаемых в правой части в нуль. Но здесь задача упрощается, поскольку числитель первого решения обращается в нуль на первом корне знаменателя и числитель второго решения обращается в нуль на втором корне знаменателя Следовательно, оба решения представляют собой сократимые дроби Осталось вычислить числа и Для них очевидны выражения Выполняя деление двучлена на одночлен, вычисляются числители рассматриваемых 5 дробей В результате получаются искомые аналитические решения для абсциссы первой вершины правильного треугольника Полученные решения позволяют выявить и случаи, когда то или иное решение не реализуется. Геометрическая интерпретация решений. Представление параметров аналитического решения в терминах тригонометрических функций углов наклона исходных лучей относительно базового луча и выражение числа в терминах углов искомого треугольника рассматриваемые решения приводятся к рациональным функциям от элементарных тригонометрических функций, измеряемых в прямоугольных треугольниках где представляет собой угол между двумя лучами и . По определению решения и представляет собой проекции на базовый луч вершины искомого треугольника, лежащей на прямой . Тогда длина отрезка от начала координат до второй вершины треугольника, определяемая данными решениями Исследование решений. Данные решения получены при условии, что вершины равностороннего треугольника лежат на трех прямых, что является более слабым требованием по сравнение с условием задачи. Для перехода к более сильному ограничению, требующему принадлежность вершин треугольника трем лучам, следует лишь подчинить полученные решения дополнительным условиям 6 означающим, что вторая точка искомого треугольника лежит действительно на луче, но не на линии, являющейся его продолжением за точку При чем выполнение обоих условий свидетельствует в пользу существования двух правильных треугольников. Если же одно из условий не выполняется, то соответствующий правильный треугольник не существует. Если же то поставленная задача не имеет геометрического решения. Сравнение результатов показывает, что если рассматривать их как функции углов между лучами, то можно заметить между ними симметрию показывающую, что построив одно решение, из него можно получить и другое решение. Более подробно рассматриваются геометрические построения первого решения. Второе решение – лишь схематически. Геометрические построения первого решения. С целью облегчения геометрических построений с помощью циркуля и линейки, результат следует выразить в терминах функции косинуса (5) с тем, чтобы при построении треугольников легко строить угол к прилежащему катету или гипотенузе. Следуя приведенному решению, геометрическое построение правильного треугольника состоит из трех шагов. На первом шаге строится вспомогательный луч под углом к базовому и на нем - точка являющаяся основанием перпендикуляра, опущенного из точки на вновь построенный луч. Рис.2. Построение точки - второй вершины треугольника На втором шаге относительно вспомогательного луча строится новый луч под углом В результате на пересечении нового луча и построенного перпендикуляра возникает новая 7 точка луче . В результате отрезок должен совпадать с длиной , отложив которую на возникает точка второй вершины искомого правильного треугольника. И наконец, третий – заключительный шаг – восстановление на луче третьей вершины Рис.3. Восстановление третьей вершины треугольника В результате возникает правильный треугольник аналитическому решению (5). Геометрические построения второго решения последовательности путем построения луча под углом соответствующий первому выполняются в той же к базовому и затем луча под углом к вновь построенному, и таким же образом строятся вершины равностороннего треугольника. и второго Рис. 4. Построение второго равностороннего треугольника Но прежде аналитическое выражение второго решения приводится к виду, 8 облегчающему геометрические построения (6) В результате возникают два равносторонних треугольника.